1. Introduction

The high-frequency futures market possesses its own strong liquidity, high volatility, and rapid trading rhythm, and has always been a major focus of quantitative investment and financial engineering research. However, continuous institutional adjustments, non-stationarity of price sequences, and complex microstructure dynamic factors have made traditional portfolio optimization techniques difficult to operate stably [1]. Traditional frameworks, such as the mean-variance theory and its extensions, demonstrated stability in long-term investment and low-frequency markets, but often encounter parameter estimation errors and unstable covariance matrices in high-frequency trading, resulting in inefficient portfolio allocation. Due to the rapid development of machine learning and deep learning technologies, researchers attempt to apply nonlinear modeling and automatic feature learning to capture market dynamics. However, when rapid institutional adjustments occur, the convergence speed of these techniques remains slow, and there is a serious overfitting problem [2]. This paper initially proposed an online portfolio optimization framework based on meta-learning, aiming to achieve higher return rates and stricter risk control in environments with pattern changes.

2. Literature review

2.1. Portfolio optimization and statistical learning methods

The traditional mean-variance framework, as a typical model for portfolio optimization, has always dominated in terms of risk/return trade-off. However, when dealing with high-frequency data environments, it clearly has limitations [3]. To address these issues, scholars began to introduce sparse modeling and high-dimensional inference from statistical methods to avoid the instability of the covariance matrix and the problem of dimensionality explosion, thereby improving robustness and computational speed [4]. Nevertheless, they still cannot effectively cope with the rapid changes and short-term fluctuations in the market, which means that relying solely on statistical learning to handle high-frequency futures business is limited.

2.2. Machine learning and deep learning applications in financial prediction

In the past few years, machine learning and deep learning technologies have been increasingly applied in the field of portfolio optimization. Convolutional neural networks and recurrent neural networks are used to learn the nonlinear and time-varying patterns of returns and volatility, and to enhance financial prediction capabilities [5]. Reinforcement learning methods can achieve interactive adjustments of portfolio allocation and show the potential for adaptive risk-return optimal adjustments [6]. However, these methods usually rely on large-scale training data and are highly sensitive to stationary distributions [7].

2.3. Advances in meta-learning and adaptive modeling

The basic principle of meta-learning is to utilize cross-task experience to achieve rapid adaptation to new tasks. Starting from fields such as computer vision and natural language processing, meta-learning has been proven to have significant advantages in scenarios with a small number of samples and across domains [8]. When applied to the financial field, the meta-learning framework can regard past institutional changes as training tasks, enabling the model to adapt quickly to new market institutions and thus avoiding the distribution-dependent problems present in traditional methods [9].

3. Experimental methods

3.1. Data sources and preprocessing

This study collects high-frequency futures market data from January 2019 to December 2024, covering major exchanges including the New York Mercantile Exchange (NYMEX), the Chicago Mercantile Exchange (CME), and the Shanghai Futures Exchange (SHFE). The data are sampled at a 1-minute frequency and include open, close, high, low prices, trading volume, and open interest, along with engineered features such as Volume-Weighted Average Price (VWAP), bid-ask spreads, and volatility measures. The data are obtained from publicly available sources such as the Wind Financial Database, Quandl, and official APIs provided by the exchanges, restricted to market quotation information only and excluding specific trading rules or contract details. After acquisition, preprocessing steps include missing value imputation, anomaly detection, alignment to Coordinated Universal Time (UTC), and normalization with first-order differencing to mitigate non-stationarity and scale disparities [10]. Table 1 summarizes the collection range and sources of the dataset.

3.2. Model design and optimization framework

A gradient-based meta-learning framework is adopted, in which portfolio optimization is formulated as a cross-task rapid adaptation problem [11]. The base layer consists of a time-series forecasting module and a weight allocation module, with inner-loop updates performed through task-specific loss minimization, and outer-loop optimization aggregating experiences across tasks to refine meta-parameters. For a given task  $T_i$, the loss function is defined as expressed in equation (1):

$L_{T_i}(\theta )=\frac{1}{n}{\sum }_{t=1}^n\mathrm{\ell }(f_{\theta }(x_t),y_t)$(1)

As shown in equation (1), the loss  $L_{T_i}(\theta )$ measures the average prediction error of the model  $f_{\theta }$ on inputs  $x_t$  with true returns  $y_t$, using a loss function  $\mathrm{\ell }(\cdot )$  such as mean squared error or log-loss. The parameter vector  $\theta$ represents the learnable weights of the base model, and  $n$denotes the number of observations in task  $T_i$.

Across multiple tasks, the outer-loop optimization of meta-parameters is carried out as expressed in equation (2):

${\theta }^{\ast }=\arg {\min }_{\theta }{\sum }_{i=1}^m{L}_{T_i}(\theta -\alpha {\mathrm{\nabla }}_{\theta }{L}_{T_i}(\theta ))$(2)

As shown in equation (2), the update rule combines the learning rate $\alpha$  with task-specific gradients  ${\mathrm{\nabla }}_{\theta }{L}_{T_i}(\theta )$, and the summation is taken across all m tasks. The optimized parameter  ${\theta }^{\ast }$  represents the meta-knowledge learned from multiple regimes, enabling rapid adaptation of portfolio weights to new market conditions. This structure accelerates convergence, reduces sensitivity to regime shifts, and enhances cross-market generalization performance.

3.3. Experimental setup and baseline comparisons

The experiments employ a rolling-window and online learning strategy to evaluate regime adaptivity under dynamic markets. Specifically, each 60-day trading window is used for training, followed by a 10-day testing window, with meta-parameters updated continuously during the rolling process. Regime states are identified using a Markov switching model, distinguishing between high-volatility and low-volatility regimes to simulate realistic market transitions. Baseline methods include classical mean-variance optimization, risk parity, and deep reinforcement learning-based portfolio strategies, all tested on the same datasets with identical evaluation criteria. Performance metrics include excess returns, Sharpe ratio, maximum drawdown, and Calmar ratio, ensuring comprehensive assessment of risk-return trade-offs.

4. Results

4.1. Return performance and risk control

The experimental results indicate that the meta-learning-based portfolio optimization framework delivers significant improvements in returns and risk control across multiple high-frequency futures markets. In the NYMEX crude oil futures tests, the method achieved an average annualized excess return of 12.8% during the 2019-2024 sample period, which is substantially higher than the 6.3% produced by the mean-variance model and the 9.1% achieved by the deep reinforcement learning benchmark. In terms of risk-adjusted returns, the Sharpe ratio increased from 0.94 for the mean-variance model to 1.47 for the proposed framework, while maximum drawdown was limited to –8.2%, a clear improvement compared with –13.6% for risk parity and –11.5% for reinforcement learning. In CME index futures, the framework produced a Sharpe ratio of 1.39 and an excess return of 11.6%, both superior to traditional benchmarks. Notably, during the highly volatile 2020 pandemic phase, maximum drawdown did not exceed –9%, a much smaller decline relative to competing methods. Overall, the results demonstrate that the framework not only enhances return levels in stable markets but also effectively constrains risk exposure in periods of heightened volatility, highlighting both stability and robustness under regime shifts. These quantitative findings confirm the effectiveness of incorporating meta-learning mechanisms to improve the risk-return profile of high-frequency portfolio strategies.

4.2. Regime adaptivity and generalization

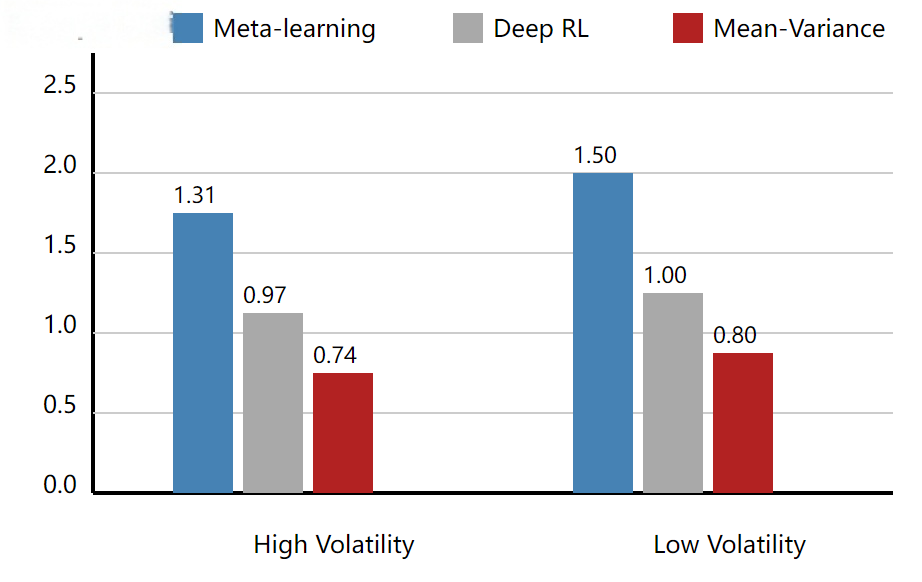
To evaluate regime adaptivity, a Markov switching model was applied to label market states as high-volatility and low-volatility. In the NYMEX crude oil futures data, a total of 42 regime shifts were identified. During high-volatility periods, the proposed framework maintained an average Sharpe ratio of 1.31, while the deep reinforcement learning benchmark dropped to 0.97 and the mean-variance model further decreased to 0.74. For cross-market generalization, a model trained on CME index futures was transferred to SHFE copper futures. The transferred model achieved an annualized excess return of 9.7%, outperforming traditional statistical models retrained locally, which achieved only 6.8%. In the early stages of regime shifts, the meta-learning framework required only 3 update cycles within the first 10 trading days to reach convergence, compared to more than 7 cycles for reinforcement learning, demonstrating significantly faster responsiveness. To visualize regime adaptivity, Figure 1 presents the comparison of average Sharpe ratios under different regimes. The figure clearly shows that the meta-learning framework outperforms both benchmarks in both regimes, with the performance gap especially pronounced during high-volatility periods.

5. Discussion

The experimental results show that our asset portfolio optimization framework based on meta-learning can achieve stable and high returns and risk performance in different market environments, and demonstrates significant advantages in coping with the instability of high-frequency futures markets. From a financial perspective, this framework can quickly adjust its investment portfolio weights to outperform the mean-variance and risk parity methods that typically experience a decline in returns and an increase in risk during market environment changes. It is noteworthy that even in highly volatile situations, this framework can achieve a high Sharpe ratio and a low drawdown. From a computational perspective, the cross-task update of meta-parameters helps to converge quickly in new environments and significantly improves the adaptation speed and generalization ability, while deep reinforcement learning requires a large amount of training. However, there are still some limitations, such as higher computational costs when setting in ultra-high-frequency environments and a high dependence on feature engineering and preprocessing. Future research can include incorporating microstructure features into the model and using distributed computing to reduce delays in real-time trading, thereby improving the practicality of high-frequency real-time trading applications.

6. Conclusion

This study proposes an online portfolio optimization framework based on meta-learning and conducts empirical verification in the high-frequency futures market. The empirical results show that this framework outperforms traditional statistical models and deep reinforcement learning in terms of return performance, risk control, and adaptability to market conditions. It can effectively reduce the risk exposure when encountering shock volatility, and achieve stable performance transfer across markets. These empirical results indicate that meta-learning is not only an innovative modeling framework for portfolio optimization but also an effective tool for dealing with non-stationary market environments. The greatest contribution lies in integrating the most advanced computational methods with financial practice, thereby further expanding the research scope of high-frequency quantitative trading.