1. Introduction

Reinforcement learning (RL) has been established as a core part of the development of autonomous agents in complex high-dimensional environments, and two seminal algorithms, Deep Q-Network (DQN) [1] and Proximal Policy Optimization (PPO) [2], greatly reshaped the domain. Dueling network DQN was the first approach to apply deep convolutional networks to approximate the action-value functions and reached human-level performance on Atari benchmarks. In contrast, PPO is an improvement of the policy-gradient class of algorithms, enabling stable and sample-efficient updates for both discrete and continuous action spaces. These correspond to the value-based and policy-based paradigms in contemporary RL.

Doing so, although producing systems that were successful in domains where strict control over action is desired like autonomous-driving simulators, and game-playing agents that plan a few moves ahead [3,4], which one to use between value-based DQN and policy-based PPO is essentially empirical. Though it is based on anecdotal evidences, DQN performs better at the early stage but can become unstable at the later stage, and PPO converges smoother albeit taking a longer time to achieve the same star t. However, there are very few systematic studies that measure such trade-offs under uniform hyperparameter settings, hence a concrete choice of an algorithm remains a challenge.

To bridge this gap, we offer a comparison between DQN and PPO in terms of convergence speed, learning stability, sample efficiency, and computational overhead. We first provide a brief theoretical overview of the parameter update rules, sources of variance and per-step time complexity for each of the algorithms. To the next step, our experimental framework uses two canonical benchmarks—CartPole in discrete domain and CarRacing in continuous domain—running a custom Metrics Callback to collect several key measurements: episodes to reach a baseline reward, variance of the episodic returns, average return per thousand steps (as a sample-efficiency proxy), and total wall-clock training time.

Through a fusion of theory and empirical evidence, we deliver three main advances. First, it offers specific and actionable advice for the practitioner for choosing and tuning RL algorithms in new domains. Second, it exposes a tradeoff between fast value-based learning and more gradual policy-based approaches. Lastly, we provide our open-source implementations of the unified evaluation framework to promote future works and extensions. Taken together, these results provide insight into DQN and PPO and contribute to enabling the practical application ofRL in real systems.

2. Comparative analysis

This chapter provides a comprehensive analysis of Deep Q-Network (DQN) and Proximal Policy Optimization (PPO), two prominent reinforcement learning algorithms. By examining their performance across various metrics in both discrete and continuous action spaces, we aim to elucidate their respective strengths and weaknesses and offer practical guidelines for selecting the appropriate algorithm for specific task requirements.

Deep Q Network (DQN) is widely used for discrete-action problems, leveraging neural networks to estimate action values (Q-values) and select optimal actions [1]. Recent theoretical work by Zhang et al. further supports this by demonstrating the geometric convergence and explicit sample complexity bounds of DQN under practical ε-greedy exploration strategies, thus providing rigorous theoretical backing for its superior stability and rapid convergence in discrete action environments [5]. Its defining features include experience replay and a fixed target network, both of which help stabilize training and enhance sample efficiency. During each update, DQN replays past experiences to break correlation between samples, while a separate target network is used to mitigate the rapidly shifting Q-value estimations. Due to these mechanisms, DQN frequently converges more quickly in discrete-action tasks such as CartPole, where only a small set of actions is available (e.g., moving a cart left or right to balance a pole).

Proximal Policy Optimization (PPO) is a policy-gradient method that operates effectively in continuous-action spaces [2]. Son et al. introduced Gradient Informed PPO, incorporating analytical gradients into the PPO framework, which significantly improves performance by adaptively managing gradient variance. This enhancement further underscores PPO’s robustness and adaptability in handling complex, continuous-action tasks requiring fine-grained control [6]. By directly optimizing the policy, PPO adjusts the distribution of possible actions. Its clipping mechanism serves to limit the extent of policy updates, thereby preventing large, destabilizing shifts in action distributions. The clipped objective function ensures that each policy update remains within a stable range, leading to smoother convergence and generally improved stability in more complex environments. A key distinction between DQN and PPO lies in their decision-making processes: DQN updates its Q-value function and selects actions from a discrete set based on estimated action values, whereas PPO refines a continuous policy through iterative adjustment of probabilities for each potential action, making it particularly suitable for tasks requiring fine-grained control.

This study chose two benchmark environments from the OpenAI Gym [4]: CartPole, a classical discrete-action environment where the agent must keep a pole balanced atop a moving cart, and CarRacing, a more complex, continuous-action environment challenging the agent to navigate a race track. All experiments were conducted using Stable-baselines3 [3], and we fixed parameters and random seeds for reproducibility. A custom callback function (MetricsCallback) was integrated to record crucial training data in real time. The performance of the algorithms was evaluated using four key metrics: Convergence Speed, measured as the number of episodes required to achieve a predefined target reward; Stability, quantified by the standard deviation of the obtained rewards; Sample Efficiency, assessed by the average reward achieved; and Computational Complexity, determined by the total training time.

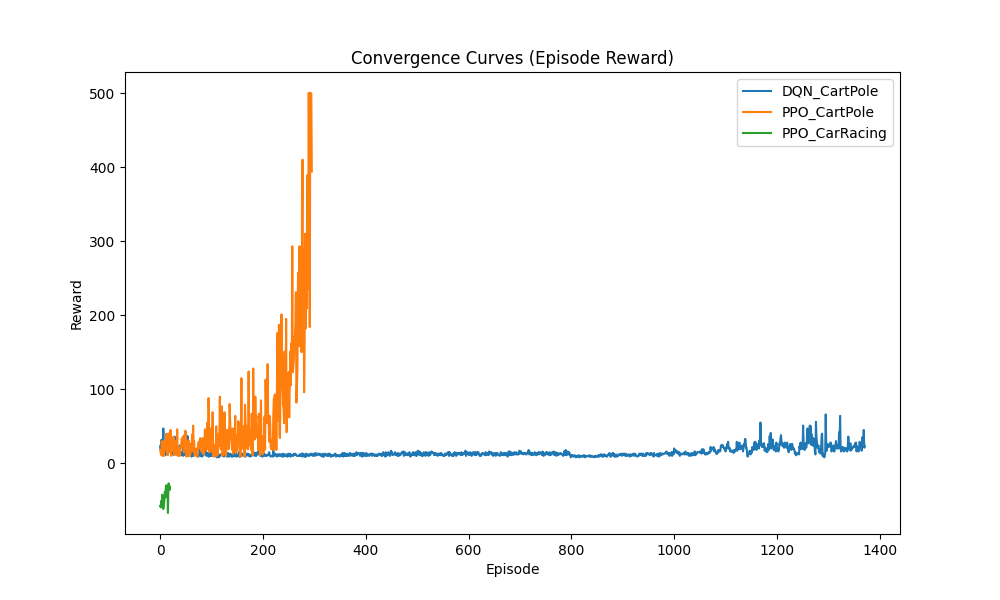
Figure 1 shows reward convergence curves of PPO and DQN in the CartPole and CarRacing environments. In the CartPole environment, DQN exhibits faster convergence to higher reward values and relatively strong stability. The experience replay mechanism empowers DQN to repeatedly leverage past successful actions, thereby accelerating the learning process. Conversely, while PPO demonstrates more robust convergence, it tends to do so at a slower pace in discrete-action tasks like CartPole. This is primarily because policy-gradient methods often necessitate a greater number of updates to achieve performance comparable to DQN. Nevertheless, in continuous-action environments such as CarRacing, PPO exhibits a superior ability to capture fine-grained control signals, resulting in a smoother and more stable convergence, albeit potentially with a slower initial training phase.

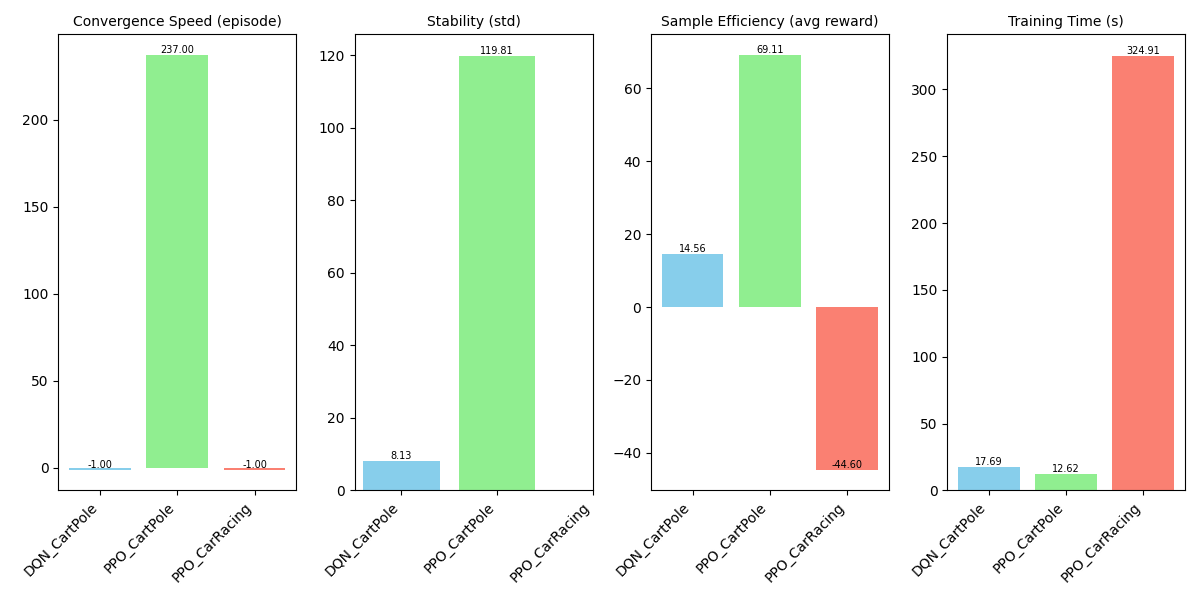
To further illustrate the performance, we plotted a bar chart comparing the metrics, offering a clear display of differences in convergence speed, stability, sample efficiency, and computational complexity. As shown in Figure 2, in the CartPole environment, DQN converges significantly faster, exhibits relatively good stability, and achieves higher sample efficiency. However, in terms of computational complexity, PPO is superior, taking less time. In the continuous action-space environment CarRacing, PPO’s advantages are more pronounced, particularly in stability and sample efficiency, indicating greater strength in handling complex decision-making tasks. Nevertheless, PPO converges more slowly and incurs a higher training cost.

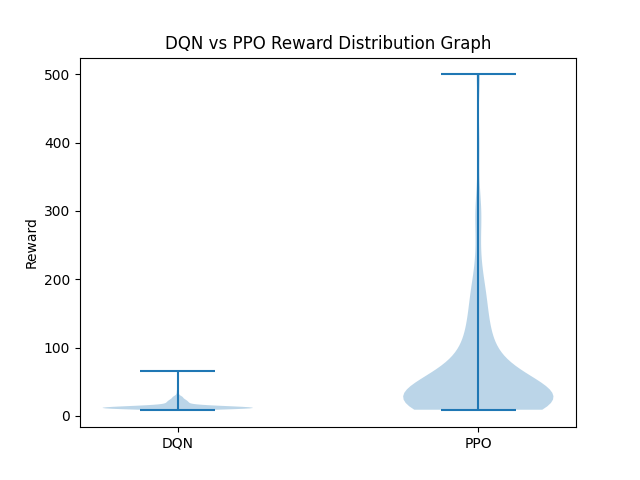
Moreover, we produce a violin plot of the reward distributions across all evaluation episodes for DQN and PPO. The width of a portion of the violin in this plot represents the density of observation counts for a given reward value, such that the thinner portions reflect fewer episodes reaching these rewards, while the wider ones represent relatively more. For DQN, the violin is very tall yet very slim, with most of the mass being around low rewards (around 10-20). They highlight the campaniform tail region of the predicted species, besides the small size of the petiole and the presence of caducous petiolar hairs. The middle white dot indicates median reward, and the thin vertical line shows interquartile range: both are “hugged” together, once again emphasizing DQN’s accuracy and robustness in the case of a discrete action set. In contrast, the violin of PPO is broader with longer upper and lower tails. The wider central region indicates that the reward PPO can often achieve is between 20 and 50 points (with occasional peaks above 100 points). This wider spread illustrates PPO’s flexibility and it’s greater likelihood to explore a variety of behaviors, although it does so with more variability. These features are indicative of the inherent strengths of each algorithm: DQN’s stability, as opposed to PPO’s potential for exploration.

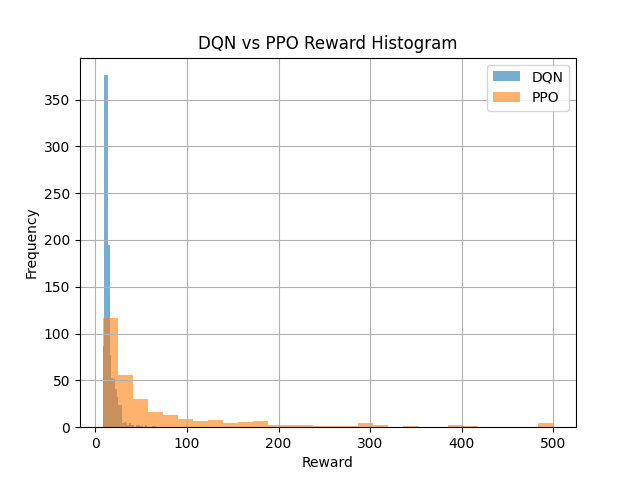
Besides that. we divided the reward dimension into regularly-spaced bins (e.g., with a 5 points interval) and we computed how many episodes ended with a reward which is in each of the bins. The DQN histogram shows a single sharp peak in the lowest bin (5-10 points) with a rapid decline as rewards become higher. This suggests that the majority of the DQN training is at relatively similar, high-reward levels, and episodes rarely reach peak performance. Beyond the first few bins, the bar heights fall off quickly, indicative of low variance. In comparison, the PPO histogram shows more spread out flatter distribution. While PPO has also a mode at moderate rewards 15-20 points, the bars of which decay more slowly, with visible counts in bin up to 200-300 points. The long right tail shows PPO’s occasional achievement of very high rewards, even if such events are rare. This heavy-tailed distribution highlights PPO’s ability to produce high-performance outliers and diverse exploration, while DQN’s robustness lies mainly in that narrow performance band.

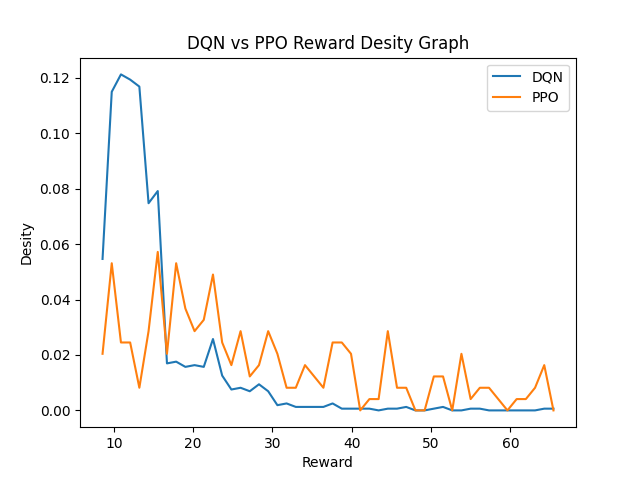
A density graph produced by applying kernel density estimation (KDE) to smooth the discrete counts in the reward distributions of both algorithms which shows the continuous patterns underlying them is depicted in Figure 5. The x and y axes stand for rewards and the estimated probability density, respectively. DQN’s KDE curve has just one big peak, directly pertained around its median reward (about 12 points) with a steep valleys on both sides of the peak. The steep drop in density around the peak in DQN verifies that the outcomes are highly concentrated and few attempts are made to explore higher or lower reward states. Interestingly, unlike other methods, PPO’s KDE curve is multimodal and has one main peak near 25 points, and secondary peaks at higher reward ranges(around 60 and 120). These multiple modes are indicative of PPO exploring many different types of performance regime: regular, frequent modest rewards and rare bursts of high rewards. The smoothness and spread of the curve for ppo reflects its underlying flexibility and adaptability in continuous-action spaces. These density estimates taken together provide granular insight into how each algorithm trades off exploitation and exploration across the range of reward outcomes.

These results further clarify that DQN is more suitable for discrete action spaces where quick convergence and high stability are prioritized, whereas PPO holds greater advantages in continuous action spaces and more complex tasks. In practical applications, one should select the appropriate algorithm according to the specific task requirements and resource constraints to achieve optimal outcomes.

A comprehensive analysis shows that DQN has a clear advantage in discrete action spaces, while PPO performs better in continuous action spaces. Therefore, in real-world scenarios, the choice of algorithm should be based on the nature of the action space in a given task, in order to attain the best decision-making performance.

Through this study, we conducted a systematic theoretical analysis and experimental evaluation of DQN and PPO, two classic reinforcement learning algorithms, thereby clarifying their performance characteristics and differences in application contexts across various metrics. The experimental results show that PPO demonstrates a clear advantage in continuous action spaces (such as the CarRacing environment), featuring faster convergence and greater stability. Meanwhile, DQN exhibits higher sample efficiency and computational efficiency when solving problems in discrete action spaces (such as CartPole).

3. Conclusion

A comparative analysis of DQN and PPO across four key dimensions—convergence speed, stability, sample efficiency, and computational complexity—reveals their distinct advantages in different scenarios. DQN generally exhibits faster convergence in discrete-action tasks like CartPole, attributed to its effective Q-value estimations that facilitate optimal action selection. Conversely, while PPO may initially require more iterations, it demonstrates greater robustness over time, particularly in continuous-action environments such as CarRacing.

Regarding stability, DQN gains from experience replay and target networks to mitigate training fluctuations, yet can become volatile in high-dimensional continuous spaces. PPO employs a clipped objective function that limits excessive policy updates, thereby delivering smoother performance and reduced variance in more complex settings.

Concerning sample efficiency, DQN excels in discrete environments by frequently reusing historical data, thus improving decision accuracy in fewer steps. However, PPO’s direct policy optimization method is advantageous in continuous domains, as it circumvents the inaccuracies and computational burdens of discretizing a large action space.

Finally, computational complexity varies: DQN’s simpler structure suits low-dimensional tasks, but discretizing many possible actions in continuous scenarios drastically increases computation. PPO, although requiring multiple updates per training phase, often proves more resource-friendly by avoiding exhaustive enumeration of continuous actions.

In sum, DQN is well suited for discrete-action problems prioritizing rapid convergence and lower complexity, whereas PPO excels in continuous-action environments demanding stable, high-precision control. Future work may investigate hybrid frameworks that combine strengths from both methods, potentially broadening their applicability to a wider range of challenging tasks.

Based on these findings, we recommend choosing algorithms according to the characteristics of the action space in practical applications: for continuous-action settings requiring precise control, PPO is advisable; for discrete-action scenarios that emphasize computational efficiency, DQN is more suitable. Future research may explore hybrid or enhanced reinforcement learning frameworks that combine the strengths of both DQN and PPO, aiming to address more complex and diverse application demands. Furthermore, expanding the range of experimental environments and the scale of datasets will enhance the comprehensiveness and practical value of findings, fostering the real-world adoption of reinforcement learning algorithms in domains such as autonomous driving, robotics control, and broader intelligent decision-making systems.