1. Introduction

In today's world, rife with uncertainty, the ability to make optimal decisions in scenarios that demand significant financial or time investment is increasingly critical. A well-chosen decision in these high-stakes situations can yield substantially greater rewards than a suboptimal one. Against this backdrop, a persuasive, reliable, and scientifically grounded methodology for decision-making across various contexts is of paramount importance.

The Multi-Armed Bandit (MAB) Problem has garnered considerable attention in both academic and industry circles as a model for addressing decision-making challenges under uncertainty. The MAB problem is inspired by a gambling analogy involving slot machines with multiple levers, where the average payout of each lever is unknown. The essence of the MAB problem lies in devising a strategy that balances exploration (trying new options) and exploitation (leveraging known information) to maximize the total rewards over a series of choices. In recent years, a multitude of sophisticated MAB algorithm variants have evolved, extending well beyond theoretical studies. These algorithms have found practical applications in diverse fields such as clinical trials, recommendation systems, and wireless digital twin networks, demonstrating their significant potential [1-3].

This paper aims to deliver a thorough review and in-depth analysis of MAB scenarios and algorithms. It will begin with a foundation in theory, providing an overview of the basic model and classical MAB algorithms, along with subsequent advancements. This will be followed by data presentation and commentary on the performance of these algorithms in experimental settings. Finally, the paper will explore recent applications, current challenges, and future directions in MAB research.

2. Theoretical Foundations

2.1. Basic Model of Multi-Armed Bandits

The classical model of the Multi-Armed Bandit (MAB) problem is described as follows: There are K available actions, often likened to “arms,” each associated with a fixed but initially unknown reward probability distribution. The agent's goal in each round is to select an arm, aiming to maximize the total reward over a series of iterations [4].

In the decision-making process, exploration and exploitation occur subliminally. Ideally, exploiting the arm with the highest reward distribution in every iteration would yield the maximum cumulative reward. However, this is impractical as the reward distributions are unknown initially. Early in the process, the agent must explore to understand the performance of each arm. Based on exploration results, the agent can then estimate which arm is the best and exploit it in subsequent iterations.

This leads to the exploration-exploitation dilemma. Adequate exploration is crucial to ensure the arm chosen for exploitation is indeed the best. Using sub-optimal arms continuously could result in significant reward loss. However, minimizing the exploration phase is also important to prevent the waste of resources on sub-optimal arms. Therefore, finding a balance between exploration and exploitation is central to the MAB problem. Generally, a well-trained agent carefully adjusts the exploration phase: it maintains sufficient exploration to identify the best arm while minimizing exploration to avoid unnecessary reward loss. The discussion primarily focuses on algorithms within the stochastic multi-armed bandit setting, which provides a natural framework for most real-world scenarios [5].

2.2. Key Algorithms in Multi-Armed Bandits

Three classical MAB algorithms will be discussed in this section: Explore-Then-Commit (ETC), Upper Confidence Bound (UCB) and Thompson Sampling (TS). The formula below assume arms’ reward is 1-sub-Gaussian.

ETC shares the same idea with A/B testing and it is intuitive and intelligible. The algorithm divides the entire decision-making process into two phases: explore and commit. In explore phase, each arm is selected with equal probability over a certain number of trial rounds to collect information on each arm’s reward distribution. Subsequently, the algorithm calculates the average reward generated from each arm and sort out the arm with the best performance, then commits it and constantly utilize it among remaining iterations [6]. The key of ETC algorithm is to determine the length of exploration phase. To find the most suitable exploration phase length, it requires the knowledge of parameters of application scenario for adjustment [7].

However, given that ETC has two definitive phases, it lacks flexibility since once it fails to distinguish the best arm in explore phase, there is no mechanism to avoid exploiting sub-optimal arm constantly. In this way, UCB and TS, two algorithms achieving seamless transition between exploration and exploitation, come into discussion.

UCB adopts a different methodology to achieve dynamic trade-off between explore and exploit. To consider the uncertainty of each arm, the algorithm sets an UCB index to represent upper confidence bound, which bases on the arm’s historical average reward and exploration bonus. Standard UCB algorithm defines UCB index for arm \( i \) at round \( t-1 \) , as:

\( UC{B_{i}}(t-1)=\hat{{μ_{i}}}(t-1)+\frac{B}{2}\sqrt[]{\frac{4log{n}}{{T_{i}}(t-1)}} \) (1)

Where \( \hat{{μ_{i}}}(t-1) \) is the average reward of arm \( i \) until round \( t-1 \) . \( {T_{i}}(t-1) \) is the number of time that arm \( i \) is selected. The second term is exploration bonus, which representing the width of confidence bound, can be used to evaluate the undiscovered possible potential [8]. \( B \) is the range of all possible reward values. Exploration bonus generally decreases with the expansion of exploration times, indicating that UCB tends to explore arms that have relatively larger potential first. This methodology considers both of historical performances and uncertainty, making it a classical algorithms that achieving seamless phase transition.

TS is a randomized probability matching algorithm that bases on Bayesian principle [9]. It maintains a posterior distribution for each arm's reward distribution, which are updated based on observed rewards. After \( k \) turns iteration to enumerate each arm to get an initial reward record, TS updates the posterior distribution of arm \( i \) as:

\( {F_{i}}(t)∼N(\hat{{μ_{i}}}(t),\frac{{B^{2}}}{4{T_{i}}(t)}), t=k+1, \) … (2)

where \( \hat{{μ_{i}}}(t) \) is the average reward of arm \( i \) until round \( t \) , \( B \) and \( {T_{i}}(t) \) are as given above for the formula (1), \( {T_{i}}(t) \) is the number of samples received from arm \( i \) until round \( t \) , and \( N(µ,{σ^{2}}) \) stands for the Gaussian distribution with mean \( µ \) and variance \( {σ^{2}} \) . Then, the algorithm draws a sample from each arm's posterior distribution and selects the arm with highest sample reward to exploit.

Referring to current research, it is argued that TS performs even better than UCB in applications like advertising and recommendation, but it is not really popular in papers, which may be accounted for the lack of strong theoretical analysis for its feature of randomness.

2.3. Improved variants of UCB and Thompson Sampling

Three improved MAB algorithms will be discussed in this section: Asymptotically optimal UCB, UCB-V and a variant of TS on Beta posterior distribution achieving dynamic parameter adjustment [10, 11].

From formula (1), it is notable that the UCB index requires the knowledge of \( n \) , which implies it is not an “anytime” algorithm. On the other hand, the exploration phase of standard UCB does not grow with time, indicating the lack of a mechanism to select arms that have not been selected for long time. To improve UCB on these two caveats, an asymptotically optimal approach is introduced, whose UCB index is defined as following at round \( t \) :

\( UC{B_{i}}(t-1)=\hat{{μ_{i}}}(t-1)+\frac{B}{2}\sqrt[]{\frac{2log{(f(t))}}{{T_{i}}(t-1)}} \) (3)

Where \( f(t)=1+t{(log{t})^{2}} \) . Instead of solely a stationary function related to total round number \( n \) , asymptotically optimal UCB introduces a logarithmic function growing with current round number. In this way, the algorithm can be regarded as “anytime” since it requires no preliminary knowledge to be launched. If an arm is not explored for long time, its exploration bonus will increase with the execution process of algorithm, giving it more opportunity to be selected compared with standard UCB. Intuitively, this modification offers a more balanced exploration mechanism.

Another improvement direction considers using variance to explore more efficiently. It is called UCB-V is academia, whose UCB index is defined as [12]:

\( UC{B_{i}}(t-1)=\hat{{μ_{i}}}(t-1)+\frac{B}{2}\sqrt[]{\frac{2log{(t)}\cdot S_{i}^{2}}{{T_{i}}(t-1)}}+\frac{3Blog{(t)}}{{T_{i}}(t-1)} \) (4)

Where \( {S_{i}} \) is the sample variance of arm i’s reward. As the formula shows, UCB-V tends to explore arms whose variance on rewards already explored is large. Since variance is an important mathematic concept commonly used to evaluate data’s degree of dispersion, a small variance tends to indicate the data distribution is stable. In MAB scenario, since each arm’s reward is obtained uncertainly from its unique reward distribution, it is wise for algorithms to adjust exploration strategy to delve more into arms whose reward distribution is hard to estimate. A smaller reward variance, indicating stability, tends to imply the distribution patten is easier to estimate. While a large reward variance implies the distribution is unstable and requires more exploration attempts to handle with. UCB-V takes advantage of this intuition and offers more opportunity to arms with higher variance, achieving a more efficient exploration mechanism.

There is a variant of TS adopting dynamic-adjusting Beta distribution. It updates posterior distribution of arm \( i \) as:

\( {F_{i}}(t)∼Beta({α_{i}}+r,{β_{i}}+(1-r)) \) (5)

where \( {α_{i}} \) and \( {β_{i}} \) are normalized parameters of Beta distribution and they are updated after each round. \( r \) represents the normalized reward obtained in the current round. Compared with standard TS, this improved version tends to perform better since its posterior distribution parameters achieve dynamic adjustment, which leads to better adaptability and stability.

3. Comparative Analysis of MAB Algorithms

3.1. Methodology for Algorithm Analysis & Comparison

Regret, a crucial concept in the field of MAB is introduced to evaluate algorithms’ performance. It is defined as the total reward lost by the agent for not choosing the best arm in each round. In other words, it is the difference between average reward of selecting optimal arm and the reward gotten by the arm actually taken. Generally, the smaller the regret, the better the algorithm’s performance. In this paper, we will use the cumulative regret plots with standard deviation bar to compare and comment on each algorithm’s performance, stability and reliability.

A dataset of movie rating is selected [13]. There are 18 different genres, representing 18 arms in MAB scenario. After processing, each record in dataset is the rating a random user gave to the genre one movie belongs to. The rating ranges from 1 to 5 and records are thrown into disorder to ensure it is for genres rather than a specific movie. The optimal arm is distinguished in advance so that cumulative regret plots can be formed.

Three comparison sequences will be launched: firstly compare 10 separate trials of three classical algorithms to reveal their key features. Secondly, it is for the average cumulative regret of UCB and two UCB variant to demonstrate the improvement brought by introducing more sophisticated mechanisms. Lastly, it is for the average cumulative regret of TS and improved Beta distribution TS.

3.2. Data Presentation: Figures

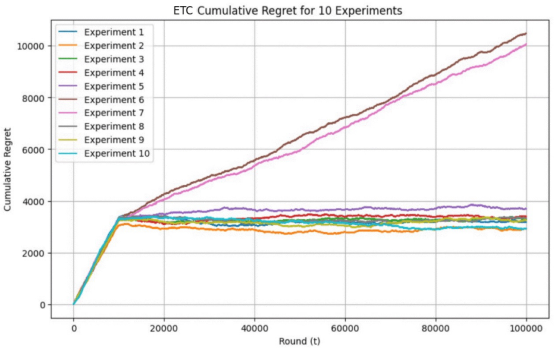
(a)

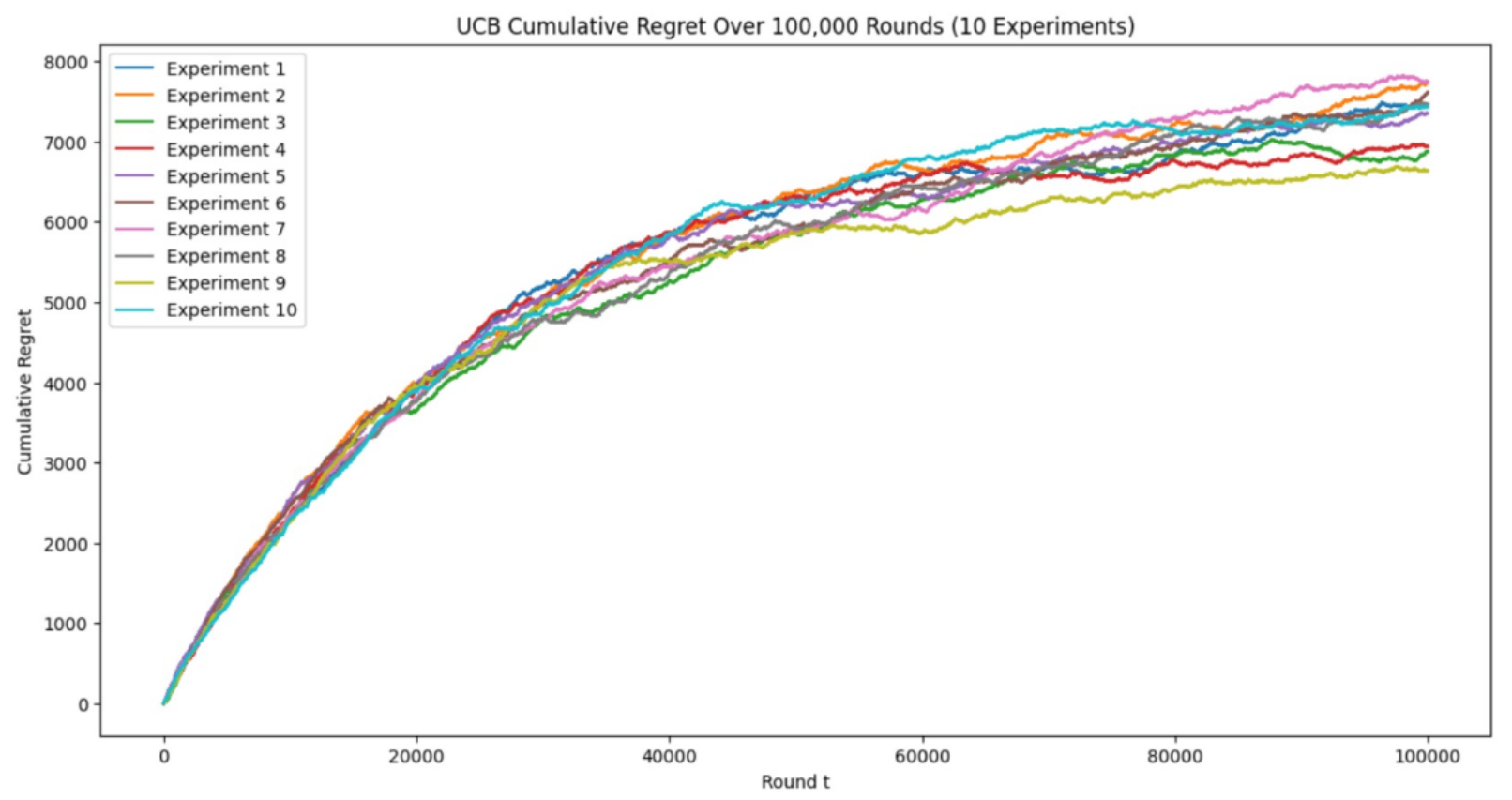
(b)

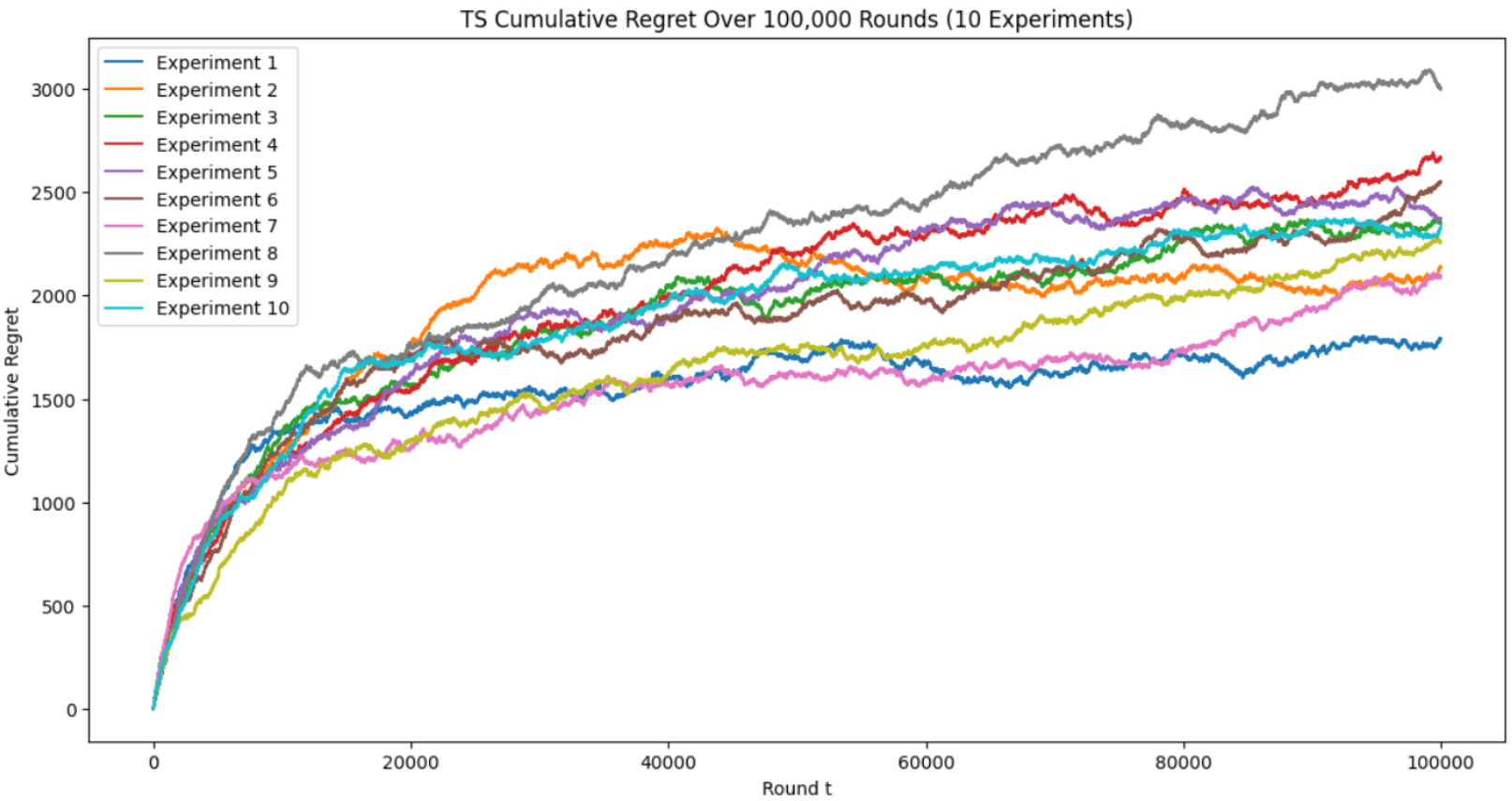
(c)

Figure 1. Cumulative Regret of ETC, UCB, TS for 10 Experiments with 100,000 Time Steps (Photo/Picture credit: Original).

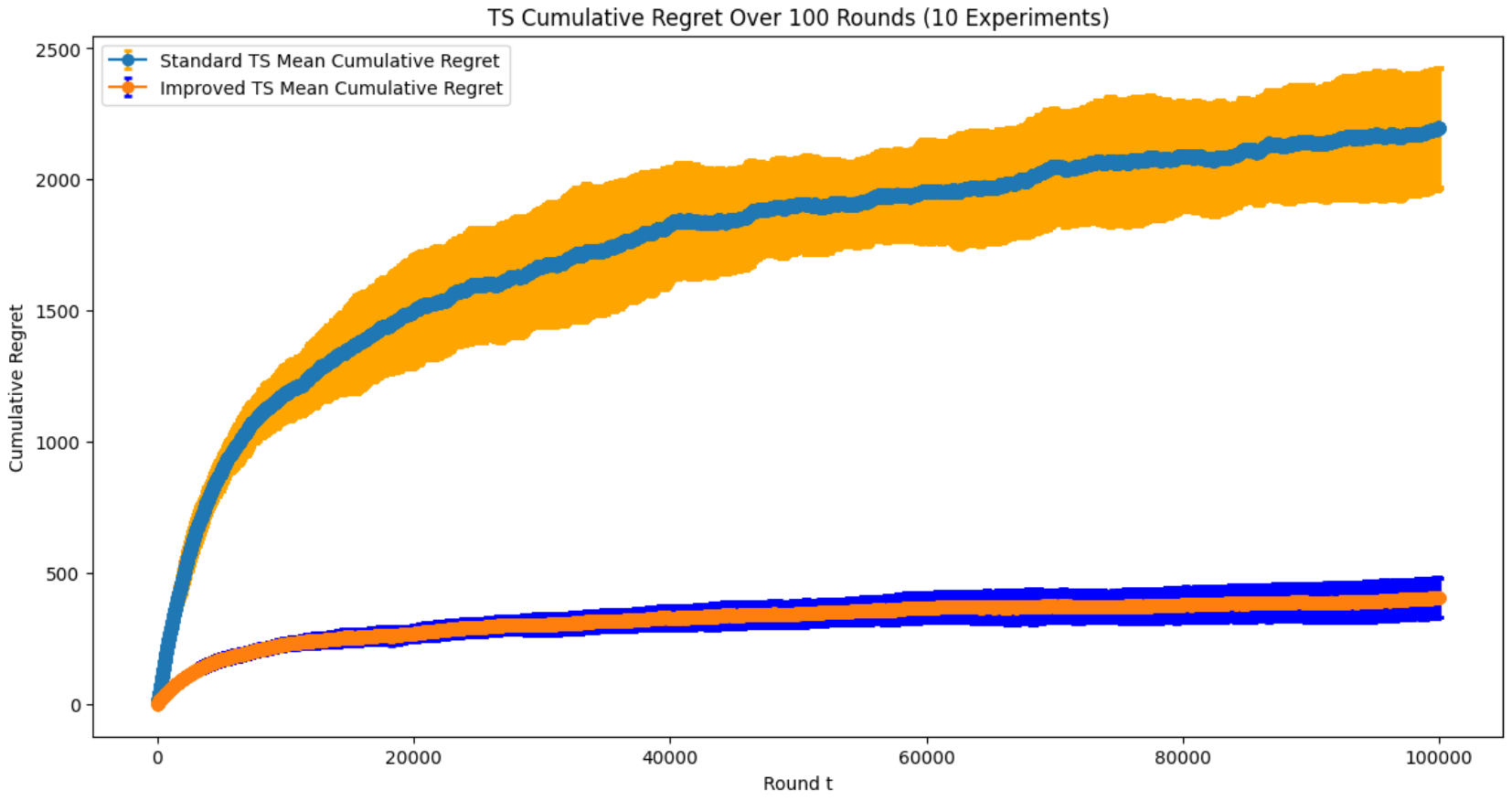
Figure 2. Average Regret of TS, improved Beta distribution TS for 10 Experiments with 100,000 Time Steps (Photo/Picture credit: Original).

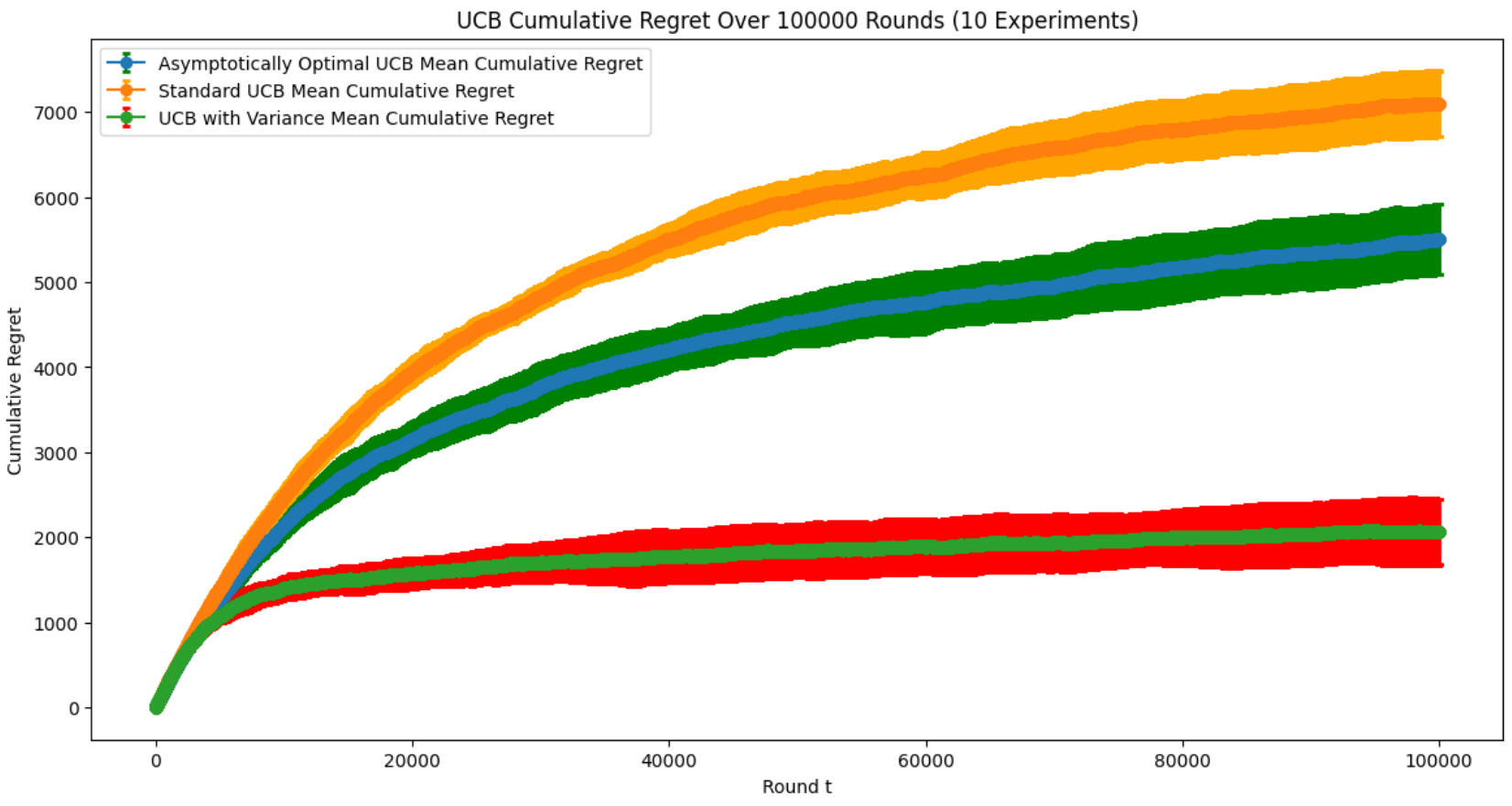
Figure 3. Average Regret of UCB, asymptotically optimal UCB and UCB-V for 15 Experiments with 100,000 Time Steps (Photo/Picture credit: Original).

3.3. Analysis of Strengths and Weaknesses

In figure 1, it is notable that 2 trials of ETC’s regret is obviously higher than the other 8. It can be explained that a great loss of reward will occur once ETC fails to distinguish the optimal arm, since it has no mechanism to correct wrong choice in exploitation phase. By contrast, TS and UCB have achieved the mechanism of smooth transferring between explore and exploit, so they can avoid the serious consequence of failing to distinguish the best arm. In this way, through ETC is efficient and simple to implement, its weakness in mechanism may constrains its more complex real world applications.

Logarithmic behavior is detected in UCB, and TS’s plots and TS performs significantly better than UCB. Its excellent performance may be due to the random arm-selection mechanism achieved by updating posterior distribution, which is conducive to efficiency and accuracy of exploration [14].

Figure 2 witnesses dramatic performance increase on TS improvement. Beta distribution TS has much smaller regret value and standard deviation, indicating its high performance in accuracy and stability. Through Beta distribution requires more calculations than Gaussian distribution, its leap in performance should be highly praised.

In figure 3, although three algorithms share proximate standard deviation, their regret value appears clear differences. UCB-V performs the best, followed by asymptotically optimal UCB, while standard UCB has the highest regret value. The difference can be explained by improvements of exploration strategies. Asymptotically optimal UCB adjusts exploration bonus for arms according to time to achieve a more comprehensive exploration. As for UCB-V, not only does it adopt this mechanism, but it also achieves differential exploration on arms based on variance to manage explore resource more wisely.

4. Applications of MAB Algorithms

Two typical MAB problem application fields will be discussed in this section.

4.1. Enhancing Recommendation Systems

A phenomenon named “information overload” is argued to have taken place in the past thirty years: users are stuck into a dilemma that they have no idea on what to buy, what to watch and what to listen to because the digital information on the Internet grows exponentially [15]. To mitigate this trend, numerous research has been conducted in the field of Recommendation System (RS), aiming to enhance user experience in online platforms. Recent research adopts Reinforcement Learning concepts to handle RS tasks, modelling it to a scenario of MAB problem to find solutions.

Several technical challenges appear to impede the development of research on RS, such as the cold start problem, data sparsity and Self-feedback Loop Bias [16]. In this section, we will discuss the meaning of each concept and summarize the nascent solution methodology in academia

The cold start problem occurs inevitably because new users do not have any previous interactions with RS. In this way, RS has no approach to learn from users’ choices to recommend on their preference. A general solution is to assign a default setting to new agents basing on the characteristics of general agents However, this approach only constrains in content-based features and fails to always perform satisfyingly. To handle the notorious cold start problem, a recent study introduced MetaCRS, a solution using meta reinforcement learning to handle cold start problem in conversational recommendation system (CRS). MetaCRS utilizes a meta policy learnt from a user population and then adapts it for new users through conversational interactions. Its learning approach adopts aspects of MAB algorithms to reconciliation the dilemma between exploration of user preferences and exploitation of known information while providing personalized recommendations. The system is consisted of three components: a meta-exploration strategy for distinguishing user preferences, an item recommendation module customized to each individuals, and a transformer-based state encoder for efficiently processing feedback. This approach requiring relatively less interaction history to provide new users with tailored and efficient recommendations, appearing significant improvements compared with existing CRS approaches [17].

Data sparsity, on the other hand, is a broader issue of incomplete information in the field of RS. It refers to the large amount of missing data in agent-system interaction matrices, leading to insufficient data for training, thus undermine the accuracy of customized recommendations. Even worse, another challenge is variation in user tastes results, which requires frequent adjustment in recommendation configuration. A joint-training algorithm, integrating dynamic user clusters and deep reinforcement learning, is introduced by a recent research. Utilizing enhanced Thompson sampling algorithm, the search aims to overcome the challenge of representation accuracy, which is crucial to maintaining recommendation efficiency since users’ preferences may change with time and other factors. Besides, the research proposed a dynamic user grouping algorithms to segment users based on their behavior pattens, achieving improvement in customized recommendations even with limited data [18].

As for another obstacle, self-feedback loop bias in RS, it refers to the bias that arises while the system is continuously trained on previous recommendations. It makes the system favors previously recommended setting, thus ignoring novel items or items that are beyond current preferred understanding range. This bias tends to persist during subsequent training since new actions generated by RS depend on previous recommendation, which may further reinforce the bias. A recent research employs Epsilon non-greedy algorithm framework to tackle the self-feedback loop bias. The framework adopts an innovative teacher-student modelling structure. The teacher model is trained on a uniformly collected unbiased dataset while the student model is trained on biased-observed data, but it is guided by teacher model to mitigate the bias. Notably, the framework employs TS algorithm to optimize exploration, which not only enhances system’s ability to recommend new relevant items to users, but it also avoids the drawback brought by overfitting biased data. Overall, comparing with existing approaches, this framework is conducive to maintain diversity and fairness of recommended content, thereby benefiting user experience.

4.2. Application in Wireless Digital Twin Networks

Wireless Digital Twin Networks (WDTN), an advanced networking concept, is introduced for solving real-life complex network problems through creating virtual mirrors of physical network environments. As a virtualization of mobile network, digital twin (DT) can update itself basing on real-time data from real network to achieve dynamic improvement on its mirrored network performance, thus returns its configuration to real work to realize actual improvement. DT has a wide range of application scenarios, including health care, aerospace and so on but its designing and training are confronted with various challenges.

In a recent research, DT placement problem is argued to be of great significance in the field of WDTN. The research points out that in order to assist the physical system successfully, it is crucial for DT implementation to capture real system network’s real-time state accurately. During this process, two aspects of cost will occur: the communication cost produced by transmitting large-scale data from devices to edge servers and calculation cost generated by processing and maintaining DT structure. In this way, a DT placement decision-making dilemma emerges: a wise strategy requires the balance between maintaining DT’s real-time accuracy and minimizing costs in communication and calculation. MAB algorithms can be applied to handle this dilemma.

The research recast DT placement problem to be a variant of budgeted-MAB problem and utilized an adopted UCB strategy to manage the trade-off between resource using efficiency and other WDTN contextual information like energy consumption. This innovative approach is evaluated to appear high performance in its efficiency and robustness, offering a possible solution with promising potential [19].

5. Challenges and Future Directions

5.1. Current Challenges in MAB Research

Through the previous sections of this paper focuses on stationary stochastic bandits, the real world scenarios tends to appear multiple more complex bandits setting, like non-stationary bandit, combinatorial bandit and so on. In non-stationary bandit, like user’s preference change, the reward distribution of arms is not fixed, making it more difficult for algorithms to predict and optimize its decision-making strategies [20]. The scenario of combinatorial bandits, each action is executed by combining multiple choices rather than select one single arm, which dramatically increases the complexity and quantity of potential actions [21].

To handle variants of bandit setting types and migrate them to real-world applications can be considered as a significant challenge in the field of MAB. These complex MAB application fields demands highly on algorithms’ mechanism improvements. The calculation load may also expand exponentially with the evolution of problem scenario, posing threat towards algorithms’ efficiency and scalability.

5.2. Prospects and Future Research Avenues

Since research on MAB problem provide aims to provide scientific methodology to guide decision-making strategies, which tends to benefit production and life, MAB has a promising research value and application potential. Theoretically, numerous research is conducted to improve algorithms’ efficiency and scalability to accommodate complex bandit settings. In the aspect of application, except of RS and WDTN which researchers are still delving into, MAB algorithms are also put into use in clinical trial, optimal warehouse allocation, multi-Cloud storage, etc [22,23].

6. Conclusion

The paper delves deeply into the Multi-Armed Bandit (MAB) problem, highlighting its significant role in decision-making under uncertainty. MAB has been effectively applied across diverse fields, demonstrating its practical impact. The paper presents classical MAB algorithms like ETC, UCB, and TS, as well as their advanced variants, offering a detailed analysis and comparison based on experimental results. Additionally, it showcases the potential of MAB algorithms in solving real-world challenges by summarizing their application in recommendation systems and wireless digital twin networks. Despite notable achievements, challenges persist, especially in adapting MAB algorithms to non-stationary environments and complex scenarios. Nevertheless, the future of MAB research is bright, with numerous theoretical and practical opportunities on the horizon.