1. Introduction

Prime numbers, as core objects of number theory research, are an important topic in mathematical research. The Riemann Hypothesis (RH), which holds the key to unraveling the distribution law of prime numbers, is not only the most challenging problem in number theory research, but also serves as a cross-disciplinary bridge connecting various branches of mathematics with disciplines such as physics and engineering, carrying humanity’s in-depth exploration of the essence of prime numbers. Meanwhile, random matrix theory, as a “super tool” connecting mathematical abstractions, physical laws, and engineering applications, provides a brand-new perspective for interdisciplinary research through its ability to describe complex systems.

In recent years, the development of data science has provided new opportunities and methodologies for studying the distribution of prime numbers and the eigenvalues of random matrices. The research attempts to further verify the potential correlation between the two through data analysis and reveal its underlying laws. This paper aims to systematically explore the statistical correlation between the distribution of prime numbers and the distribution of eigenvalues of random matrices, with data visualization and statistical analysis as core methods.

The research attempts to reveal the intrinsic connection between the prime number distribution law (especially the zero-point distribution of the Riemann zeta function) and the eigenvalue distribution of random matrices by constructing a prime number sample set and a GUE random matrix model, and completing key steps such as data acquisition, normalization processing, statistical distribution modeling, and visual presentation with the help of Python tools. This research contributes to exploring the empirical value of data science methods in addressing fundamental number theory problems and provides an interdisciplinary analysis paradigm for the research of traditional mathematical problems.

2. Literature review

2.1. Riemann hypothesis and the distribution of prime numbers

Prime numbers are special natural numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7). They are the basic units in the study of number theory, and the pattern of their distribution has always been a core puzzle in the field of mathematics. Prime numbers do not appear in natural numbers with a simple periodicity, but they exhibit an asymptotic pattern through the prime number theorem. As N approaches infinity, the number of prime numbers less than N, denoted as π(N), is approximately equal to N/logN.

In the study of prime numbers, the Riemann Hypothesis has always been central. The Riemann Hypothesis states that all non - trivial zeros of the ζ function lie on the critical line Re(s)=1/2 in the complex plane. This hypothesis is closely related to the distribution of prime numbers [1]. Many scholars have conducted in - depth research around it. Selberg proved that a positive percentage of non-trivial zeros lie on the critical line [2]. Conrey proved that at least 40% of the zeros lie on the critical line [3]. The importance of the Riemann Hypothesis lies not only in its own academic value, but also in the many equivalent propositions and hypothetical conclusions it contains. For example, dozens of important propositions in number theory can be deduced on the premise of RH [4]. Nearly two centuries have passed since the Riemann Hypothesis was proposed, and there is still no definite conclusion on its verification.

2.2. Random matrix

Data analysis research in random matrix theory provides direct support for the analogy between random matrices and prime number distribution. The prototype of random matrix theory originated from statistical and economic research in the early 20th century.S.D.Wicksell and E.T. Whittaker explored the preliminary concepts of random matrices in early economic models [5]. Subsequently, Albert Einstein conducted research on the vibration spectra of solids. He first proposed the problem of random matrices, laying the foundation for the theory of eigenvalue distribution [5]. Freeman Dyson collaborated with Wigner, applying the theory to the analysis of complex nuclear energy spectra and introducing the concept of NNSD (nearest neighbor spacing distribution) [6]. The Wigner-Dyson distribution (for highly correlated systems) and the Poisson distribution (for weakly correlated systems) have been extended to gene networks and chaotic systems [6]. Montgomery found that when u is small, R₂(u) ≈ 1-[sin(πu)/(πu)]², which is exactly the same as the pair-correlation function of GUE eigenvalues: the R₂(u) of GUE has the same form, originating from the eigenvalue repulsion effect [7-8]. Odlyzko verified this through numerical calculations, using large-scale zero-point data showing that the gap distribution P(s) is highly consistent with the GUE prediction [9].

Some progress has been made in researching the correlation between the distribution of prime numbers and the distribution of eigenvalues of random matrices. The development of data science has injected new vitality into this field. However, there are still some gaps in the research on the internal relationship between the complex prime number model and the random matrix model.

3. Methodology

3.1. Prime number normalization interval processing

One of the core characteristics of prime number distribution is the randomness of the gaps between adjacent prime numbers. However, direct analysis of raw gaps is affected by prime density. To eliminate the density deviation caused by the magnitude of prime numbers, it is necessary to perform normalization processing on the gaps.

Define the normalized interval of prime numbers: (where is the k-th prime number and is the (k+1)-th prime number).

When k is extremely large, the distribution approaches a fixed curve as follows [8].

$$$ \begin{array}{c}{\text{S}}_{\text{k}}\text{=}\frac{{\text{P}}_{\text{k+1}}\text{-}{\text{P}}_{\text{k}}}{\text{ln}{\text{P}}_{\text{k}}}\end{array}$$$(1)

3.2. Framework

3.2.1. GUE random matrix

The Gaussian Unitary Ensemble (GUE) is an important model with unitary symmetry in random matrix theory, and its matrix elements satisfy the complex Gaussian distribution [8]. The eigenvalue distribution that satisfies the GUE model has universality and does not depend on the specific matrix size (under the limit condition). It is a typical model for describing the energy level distribution of strongly correlated complex systems.

3.2.2. Wigner’s conjecture theory

Through research on the energy levels of heavy nuclei, Wigner conjectured that the energy level spacings of complex quantum systems follow specific statistical distributions, and these spacings contain universal statistical laws [6,10].

Define the normalized interval distribution as:

$$$ \begin{array}{c}\text{P}\left(\text{s}\right)\text{=}\frac{\text{πs}}{\text{2}}{\text{e}}^{\text{-π}{\text{s}}^{\text{2}}\text{/4}}\end{array}$$$(2)

4. Experiment

4.1. Experiment process

Prime number sample acquisition: With the help of the sympy library, select all prime numbers between 1 and 1,000,000. Avoid the interference of the special distribution of small prime numbers, then calculate the intervals between adjacent prime numbers and normalize them with the average interval.

Generate a GUE random matrix using NumPy, calculate and sort the eigenvalues through linear algebra tools, then obtain the intervals between adjacent eigenvalues, and also normalize them by the mean of the intervals.

import numpy as np

import matplotlib.pyplot as plt

from sympy import primerange

Experiment Process# Calculate the distribution of prime number gaps (N=10000)

primes = list(primerange(1, 1000000))

gaps = [primes[i+1] - primes[i] for i in range(len(primes)-1)]

normalized_gaps = gaps / np.mean(gaps)

Generate the eigenvalue interval of a random matrix (1000x1000)

matrix = np.random.randn(1000,1000) + 1j*np.random.randn(1000,1000)

matrix = (matrix + matrix.T.conj()) / 2 # GUE matrix construction

eigenvalues = np.sort(np.linalg.eigvalsh(matrix))

eigen_gaps = np.diff(eigenvalues)

normalized_eigen_gaps = eigen_gaps / np.mean(eigen_gaps)

4.2. Results visualization

Use Matplotlib to plot histograms of the normalized intervals of prime numbers and the normalized intervals of eigenvalues of GUE matrices using matplotlib.

Meanwhile, based on the theoretical formula of Wigner Surmise, the experimental results are presented through triple - contrast visualization (as shown in Figure 1).

plt.hist(normalized_gaps, bins=50, density=True, alpha=0.5, label=Primes)

plt.hist(normalized_eigen_gaps, bins=50, density=True, alpha=0.5, label=Random Matrix)

plt.plot(np.linspace(0,5,100), (np.pi*np.linspace(0,5,100)/2)*np.exp(-np.pi*np.linspace(0,5,100)**2/4),k--, label=Wigner Surmise)

plt.legend()

plt.show()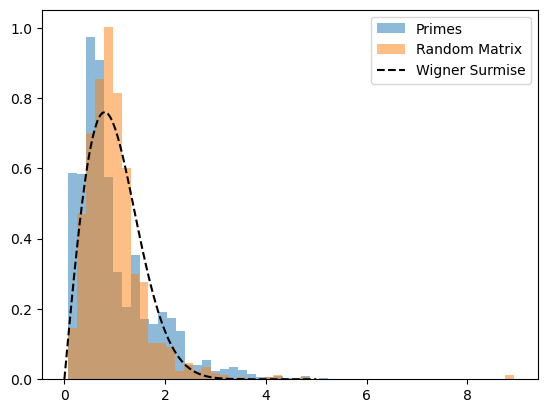

As shown in Figure 1, this study calculated the normalized gap distributions of primes and GUE random matrix eigenvalues, and compared both with the Wigner Surmise theoretical curve. The frequency distributions of the normalized intervals of prime numbers (blue) and eigenvalues of random matrices (orange) are intuitively presented through a histogram. The two exhibit a high degree of morphological similarity in the low-interval range (e.g., 0-2), which provides support for the conjecture that "prime number intervals follow the statistical laws of random matrices". At the same time, t comparing both distributions with the Wigner Surmise theoretical curve (black dotted line) quantifies the matching degree between “theoretical predictions” and “actual data (primes, random matrices)”. The relatively close trend reflects that the distribution of prime numbers conforms to the universality of random matrix theory to a certain extent. This proves that the randomness of prime numbers can be quantitatively described by the statistical model of random matrices.According to the Montgomery-Odlyzko law, the spacing distribution of the zeros of the Riemann zeta function satisfies specific rules.

Since the distribution law of prime numbers directly depends on the distribution of the non-trivial zeros of the Riemann zeta function, it is conjectured that there may also be a certain relationship between the distribution of the non-trivial zeros of the Riemann zeta function and the normalized spacing distribution of the eigenvalues of the GUE matrix. By using Python code, numerical calculations are carried out with NumPy, and plotting is done with Matplotlib.

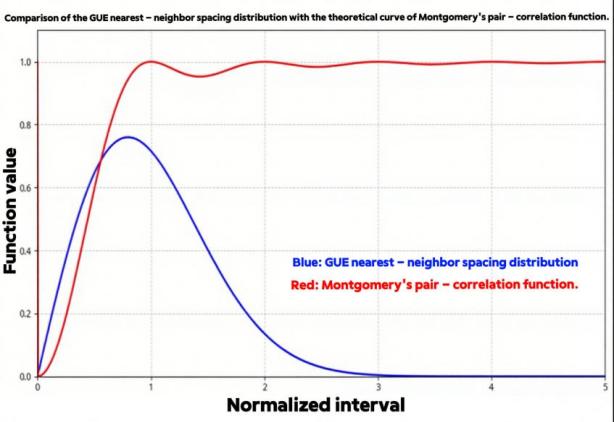
According to Figure 2, it is found that after the normalized interval is greater than 1, the difference between the theoretical curves is significant. It is speculated that the interval distribution of the zeros of the Riemann zeta function and the GUE nearest-neighbor spacing distribution may exhibit different characteristics with the change of the normalized interval.

5. Discussion

5.1. Conclusion

This study explored the relationship between random matrices and primes using visualization tools, confirming statistical similarity between the normalized spacing distribution of primes and the eigenvalue distribution of GUE random matrices. In particular, there is a significant morphological consistency was observed in the low-spacing interval (0-2). Moreover, both of them show a high degree of agreement with the Wigner Surmise theoretical curve. This discovery helps to support the idea that the distribution of prime numbers contains the universal laws of complex systems.

From an application perspective, this paper provides new insights for improving encryption algorithms. A more efficient prime number generation algorithm is generated through the random matrix model, and its randomness helps to ensure the dependence of RSA encryption on the randomness of prime numbers [10]. Additionally, while this research cannot directly prove the Riemann Hypothesis, it provides empirical support for the correlation between prime distribution and complex system laws using large-sample data. It also offers a new perspective for exploring number-theoretic problems through data science methods and provides certain theoretical support for subsequent exploration of the deep-seated connection between the zeros of the ζ function and complex systems.

5.2. Limitations

This experiment also has certain limitations. Firstly, the model scope is narrow. This study only focuses on the eigenvalues of prime number distribution and random matrices (GUE model), and does not explore other symmetric types of random matrix ensembles (GOE or GSE). Since there are slight differences in the eigenvalue distributions of different matrix ensembles, further research is needed to examine the correlation between prime number distribution and multiple ensembles to verify its universality.

Secondly, quantitative analysis is insufficient. There is a shortage of quantitative statistical data on the distribution of prime numbers and matrix eigenvalues, and most of the focus is on qualitative observation of images and distribution patterns. Consequently, subtle differences or unique distribution characteristics in local intervals (such as the degree of deviation in large - interval regions) may be overlooked. Finally, sample coverage is limited. Future studies could expand the sample size of Riemann zeta-function zero (by calculating more zeros) to verify the asymptotic stability of the distribution pattern.

6. Conclusion

This paper reveals the similarity between prime number distribution and random matrix eigenvalue distribution through empirical analysis. The research shows that the normalized intervals of prime numbers are highly consistent with the eigenvalue distribution of random matrices in the low-interval range, which confirms the applicability of the laws of complex systems in the field of number theory and provides a new research paradigm from the perspective of data science for solving problems in analytic number theory. However, due to experimental limitations, there are still some deficiencies in the selected samples. Therefore, further verification by incorporating other matrix ensembles is still needed in the future.

This paper combines the fine structure of deterministic systems in number theory with the universal laws of random systems in random matrix theory. It not only solves the core problems in number theory and physics but also provides new perspectives for interdisciplinary research. This “bridge between determinism and randomness” may find new application scenarios in more complex systems in the future (such as the weight distribution of neural networks in artificial intelligence and the distribution of galaxies in cosmology), thereby promoting a deeper understanding of the relationship between “order and chaos”.