1. Introduction

Over the past few years, machine learning and statistical learning methods have been widely applied in the fields of portfolio optimization and asset pricing to handle high-dimensional factor information and reveal the subtle nonlinear relationship patterns of asset returns. However, financial markets often exhibit volatility and instability, which leads to irregular distributions between the training set and the test set [1]. Classical methods lose their predictive ability and become unstable during extreme market conditions or structural institutional changes. Although there have been developments in factor modeling, return prediction, and portfolio optimization, there is currently no good solution that can provide strong theoretical guarantees and wide applicability for the strong theoretical guarantees and wide applicability under distribution changes and adversarial noise [2]. With its strict mathematical tools for model generalization, statistical learning theory has become increasingly useful in solving the difficulties in factor investment practice. Based on this, this study proposes a general guarantee framework that addresses adversarial distribution changes by combining regularization constraints and adversarial sampling to enhance the model's adaptability in non-stationary market environments [3]. This framework has been proven to be applicable to multi-factor stock selection and portfolio optimization, showing significant advantages in robustness and transferability. By combining the theoretical foundation of the financial field with practical applications, this method provides new evidence and insights for the stability and reliability of investment strategies.

2. Literature review

2.1. Machine learning methods in portfolio and factor models

Machine learning techniques have been widely applied in factor models and portfolio optimization, including regularization regression, tree models, and deep neural networks, etc. These techniques can extract nonlinear patterns from high-dimensional attributes and improve the predictive power of asset returns, but they often encounter problems such as overfitting and poor generalization ability in the actual market [4]. Academic methods mainly focus on feature selection, dimensionality reduction processing, and regularization constraints to enhance the robustness of the model, and combine economic factor frameworks to enhance interpretability [5].

2.2. Distribution shifts and financial market uncertainty

Distribution shift is an inherent feature of financial markets, often triggered by macroeconomic shocks, policy adjustments, and structural changes driven by competition [6]. The statistical patterns that the model relies on during the training phase often fail during the testing phase, resulting in a significant decline in predictive performance. Existing studies have attempted to alleviate this issue through transfer learning and domain adaptation, but these methods rely on the similarity between the source domain and the target domain. However, in a complex and heterogeneous market environment, this premise is difficult to meet [7]. Robust optimization can theoretically enhance the stability of the model, but overly conservative designs often sacrifice the potential for returns and weaken the practical application value.

2.3. Theoretical advances in statistical learning generalization guarantees

Statistical learning theory provides systematic tools for analyzing model generalization with limited samples, with representative approaches including PAC-Bayes bounds, Rademacher complexity, and stability analysis. These methods have been validated in certain financial tasks, offering upper bounds on model errors. However, most studies rely on the i.i.d. assumption, which fails in non-stationary and adversarial distribution settings, thereby limiting practical applicability [8]. Recent research has sought to integrate adversarial learning and distributionally robust optimization into the generalization framework, yet their application to multifactor stock selection remains nascent [9]. Importantly, generalization guarantees not only offer mathematical support for model validity but also establish a balance between predictive accuracy and robustness, which is particularly critical in uncertain financial markets. Thus, integrating statistical learning guarantees with distributional shift characteristics represents a crucial pathway for advancing financial machine learning from theory to empirical practice.

3. Experimental methods

3.1. Data sources and preprocessing

The experimental data are sourced from the Chinese A-share market and the US NYSE/NASDAQ market. The time period covers from 2015 to 2023, encompassing multiple dimensions such as value, growth, momentum, volatility and liquidity. All data undergo systematic preprocessing operations before being input into the model, including factor standardization processing, missing value interpolation, and removal of extreme outliers in the cross-section, to prevent extreme anomalies from causing deviations in the estimation process. Table 1 presents the categories of factors and their main indicator compositions.

The training set covers 2015–2019 for model parameter learning, the validation set spans 2020–2021 for hyperparameter tuning and adversarial regularization weight selection, and the test set spans 2022–2023 to specifically evaluate the model’s generalizability under distributional shifts.

3.2. Model design and generalization bound derivation

In model design, this study proposes an Adversarial Factor-Deep Neural Network (AF-DNN) that incorporates adversarial regularization to enhance the stability of return prediction under distributional shifts [10]. The objective function consists of the empirical loss and an adversarial regularization term, formally expressed as shown in Equation (1):

$$ \text{L}\text{(}\text{θ}\text{)=}\frac{\text{1}}{\text{n}}\sum _{\text{i}\text{=1}}^{\text{n}}\text{ℓ}\text{(}{\text{f}}_{\text{θ}}\text{(}{\text{x}}_{\text{i}}\text{),}{\text{y}}_{\text{i}}\text{)+}\text{λ}\text{⋅}\underset{\text{‖}\text{δ}\text{‖≤ϵ}}{\text{max}}\text{ℓ}\text{(}{\text{f}}_{\text{θ}}\text{(}{\text{x}}_{\text{i}}\text{+}\text{δ}\text{),}{\text{y}}_{\text{i}}\text{)}$$(1)

Where ℓ(⋅) denotes the loss function, δ represents adversarial perturbation, λ is the regularization coefficient, and ϵ constrains the perturbation magnitude.This formulation ensures that the model not only minimizes training error under the original data distribution but also maintains stable performance when subjected to adversarial perturbations.

Furthermore, based on statistical learning theory, the PAC-Bayes generalization bound of the model can be derived, as shown in Equation (2):

$$ \text{R}\text{(}{\text{f}}_{\text{θ}}\text{)≤}\widehat{\text{R}}\text{(}{\text{f}}_{\text{θ}}\text{)+}\sqrt{\frac{\text{KL}\text{(}\text{Q}\text{‖}\text{P}\text{)+}\text{ln}\text{(}\text{1/}\text{δ}\text{)}}{\text{2}\text{n}}}$$(2)

Where R(f_θ) is the true risk,  $$ \widehat{\text{R}}\text{(}{\text{f}}_{\text{θ}}\text{)}$$  is the empirical risk, KL(Q∥P) denotes the Kullback–Leibler divergence between the posterior and prior distributions, and δ is the confidence parameter. This bound illustrates that with finite samples, if adversarial regularization effectively constrains model complexity and sensitivity to distributional shifts, the generalization error on unseen data can be strictly controlled.

3.3. Experimental procedure and evaluation metrics

The effectiveness of the proposed model is validated through three experimental settings, baseline model comparisons, adversarial perturbation simulations, and cross-market transfer evaluations [11]. Baseline models include OLS multifactor regression, LASSO regression, and a standard deep neural network, ensuring that AF-DNN is benchmarked against methods with varying levels of complexity. Model parameters are trained on the training set, while the validation set is used to adjust the weights of adversarial regularization and network structures, and final evaluations are conducted on the 2022–2023 adversarial test set. The evaluation framework incorporates not only traditional financial indicators such as annualized return, Sharpe ratio, and maximum drawdown but also introduces the Robustness Index (RI), which is defined as the ratio of return variance under perturbations to baseline variance, thereby capturing model stability under distributional shifts. This index enables an intuitive quantification of changes in risk exposure across different environments.

4. Results

4.1. Comparison of baseline models and adversarial models

Empirical results on the adversarial test set (2022–2023) demonstrate that the proposed AF-DNN significantly outperforms traditional baseline methods in both return and risk control. Specifically, the OLS multifactor regression model achieves an average annualized return of 4.2%, a Sharpe ratio of only 0.61, and a maximum drawdown of -18.3%. LASSO regression shows slight improvement with an annualized return of 5.1%, a Sharpe ratio of 0.68, and a maximum drawdown of -16.9%. The standard deep neural network further improves performance to an annualized return of 6.8% and a Sharpe ratio of 0.75, but still suffers from a relatively high drawdown of -15.6%. By contrast, AF-DNN achieves an annualized return of 10.5%, a Sharpe ratio of 1.02, and a maximum drawdown reduced to -11.2%, demonstrating a superior balance between profitability and stability. The comparison of Sharpe ratios is illustrated in Figure 1, where AF-DNN’s advantage over the baseline models is clearly visible.

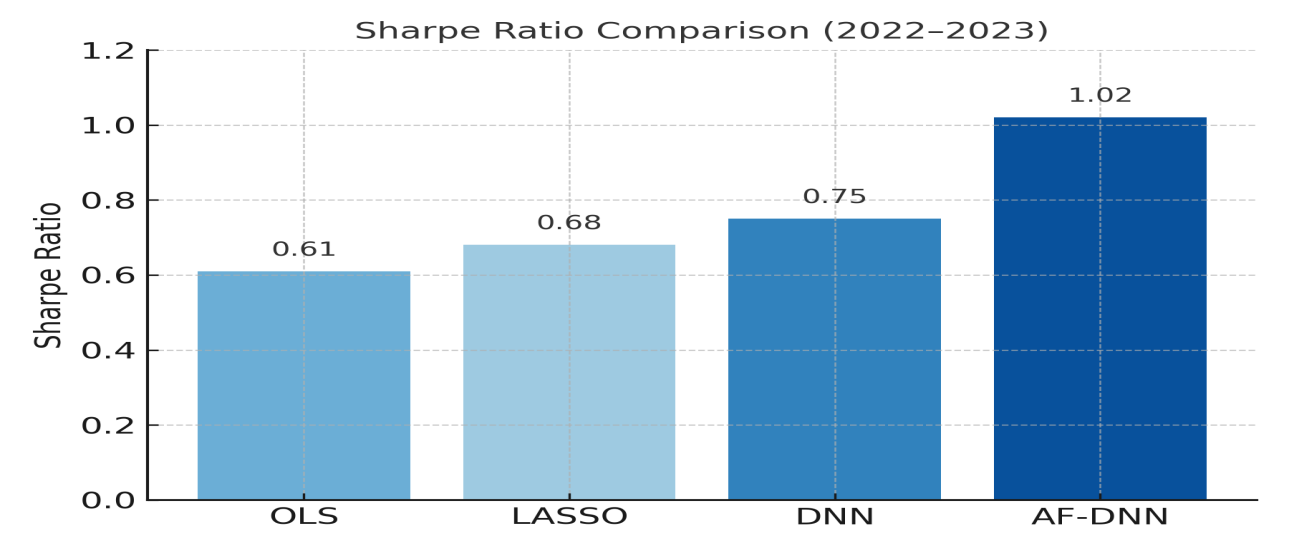
This comparison validates the effectiveness of adversarial regularization in mitigating sensitivity to distributional shifts, allowing the model to achieve not only higher returns but also stronger resilience to risk in real market conditions.

4.2. Cross-market and temporal transfer validation

To further test the robustness of the model, AF-DNN was evaluated under cross-market and time migration conditions. In the cross-market experiment, the model took China's A-shares as the training set and was directly transferred to the US market. The Sharpe ratio only dropped from 0.98 to 0.82, still outperforming OLS (0.55), LASSO (0.61), and DNN (0.70). The robustness index increased by an average of 35% compared to the benchmark method, demonstrating strong adaptability to structural differences. In the time transfer experiment, the training set was limited to 2015-2019, and the test period was COVID-19 shock (2020-2021). The Sharpe ratio of traditional models generally dropped below 0.55, while AF-DNN remained at 0.91 and controlled the maximum drawdown at -12.4%, which was significantly better than DNN (-17.2%) and OLS (-20.1%). The results show that AF-DNN has strong generalization ability in non-stationary and extreme environments. Its dynamic factor adjustment and anti-regularization mechanism effectively reduce the uncertainty of returns. It has both stable market applicability and resilience in complex situations, supporting cross-market factor investment and extreme risk management.

5. Discussion

The experimental results show that combining the generalization guarantee of statistical learning with adversarial regularization can significantly improve the robustness of the multi-factor stock selection model in the context of distribution shift. Compared with traditional OLS, LASSO and standard deep neural networks, AF-DNN not only performs better in core indicators such as annualized rate of return and Sharpe ratio, but also has achieved significant improvements in risk control dimensions such as maximum drawdown and robustness index. This highlights the potential of adversarial modeling in financial applications, by limiting the model's sensitivity to non-stationary disturbances, making it more adaptable to the complexity of the real market.

However, it should be noted that although adversarial constraints are significantly effective in enhancing robustness, they may suppress peak returns in certain scenarios, thereby creating a trade-off between returns and stability. This discovery suggests that future research should further explore multi-objective optimization frameworks, maximizing the release of benefit potential under the premise of ensuring risk control, in order to achieve long-term balance and sustainability of model performance.

6. Conclusion

This study proposes a multi-factor stock selection method based on statistical learning. By introducing adversarial regularization into deep neural networks and combining it with the PAC-Bayes generalization bound, theory and practice are closely integrated. The experimental results show that this method demonstrates outstanding consistency in returns and risk control capabilities in both the Chinese and American markets, remaining stable even in extreme scenarios or cross-market migrations (from the Chinese market to the US market). Compared with traditional models, AF-DNN not only effectively alleviates the risk of prediction failure caused by distribution shift, but also achieves significant improvements in key indicators such as maximum drawdown and robustness index, providing an important reference for asset pricing and portfolio construction. The contribution of this paper lies in introducing statistical learning theory into the empirical research of financial factor investment, proposing a new methodological path, and verifying its practicality and effectiveness through large-scale financial market data.