1. Introduction
With the advancement of urbanization, cities have entered a phase of stock optimization, leading to increased urban demolition activities and the consequent generation of massive amounts of construction waste. The disposal of such waste primarily relies on open-air dumping and landfilling, which consumes substantial land resources and exacerbates land shortages for waste disposal. Resource recovery and recycling of construction waste provide an effective solution to this problem.
Developing an optimized reverse logistics network for construction waste recycling, based on the dual objectives of cost efficiency and environmental benefits, offers a strategic approach for sustainable development. By simultaneously considering cost and environmental factors, such a model allows construction enterprises to fulfill their social responsibility for sustainable demolition while maintaining profitability, thus reconciling corporate earnings with national sustainability goals.
This study focuses on optimizing the construction waste reverse logistics network with the objective of minimizing both economic costs and environmental costs (measured by carbon emissions). The decision-making outcomes of the model include the selection of landfill centers, resource recycling centers, and the optimization of transportation routes between these nodes. The key to model optimization lies in the scientific layout of logistics nodes and the rational planning of transportation routes, thereby maximizing the overall efficiency of the reverse logistics network in terms of both economic and environmental benefits.
2. Literature review
With the growing emphasis on the green economy, reverse logistics has garnered increasing attention. In this study, construction reverse logistics refers to the process in which construction materials or equipment, having lost most of their original value during the conventional logistics cycle, are withdrawn from the existing logistics system. These materials or equipment are subsequently processed through a series of activities, including collection, classification, resource recovery, and transportation, enabling previously unusable items to regain value. Several scholars have contributed to research on reverse logistics:
Li [1] considered both cost and recovery rate in reverse logistics network design and developed a cost-recovery trade-off model for construction waste reverse logistics. His research examined the interactions between government policies and construction waste recycling enterprises, highlighting the impact of incentive mechanisms and conducting sensitivity analysis of the model. Li et al. [2] discussed two scenarios in construction waste reduction logistics: systems with on-site processing capabilities and those without. They integrated economic, environmental, and social factors to construct a multi-objective reduction logistics network model.
Zhang et al. [3] applied queuing theory to reverse logistics networks, developing a queuing system to simulate various processing capacities and operational conditions of facilities within the network on both weekdays and weekends. Vargas [4] explored the roles of stakeholders in the regulatory framework of reverse logistics for waste electrical and electronic equipment, emphasizing the collaborative efforts among municipal cleaning service providers, recyclers, and management entities in supporting an effective e-waste recycling system.
Karthik [5] highlighted that well-planned Reverse Logistics (RL) programs can reduce manufacturing costs, establish green supply chains, improve customer satisfaction, and provide competitive advantages. RL has gained increasing popularity in the automotive industry for recovering value from returned vehicles. Chu [6] proposed a new reverse logistics recycling model for express packaging in Beijing, integrating the "Internet + TPR" system to address challenges such as high investment costs, uneven profit distribution, and slow information flow for small and medium-sized enterprises.
Mao [7] emphasized that revising green logistics laws, developing integrated forward and reverse logistics service systems, and helping enterprises reduce costs and increase efficiency can accelerate the low-carbon transition of China's manufacturing logistics services.
Hajar [8] explored the relationship between reverse logistics and the circular economy, utilizing the TOWS analysis framework to identify strengths, weaknesses, opportunities, and threats, providing actionable insights for achieving a more sustainable future. Atoapem [9] examined urban management strategies for plastic waste using reverse logistics approaches. Mukherjee [10] stated that reverse logistics services aim to transfer goods from the point of consumption to their final destination, maximizing material recovery and reuse for added value or proper disposal.
Jauhar [11] proposed a two-stage intelligent emergency battery reverse logistics management system, demonstrating how recycling batteries can recover valuable raw materials, reduce landfill waste, and support environmental sustainability.
Yulieth et al. [12] introduced a bi-objective mixed-integer linear programming model for designing reverse logistics networks for economic and safe medical waste management. Sorichetti et al. [13] developed a multi-period mixed-integer linear programming model for optimizing the reverse logistics network of large-area Empty Pesticide Containers (EPCs) to achieve economic value and complete recyclability. Farida et al. [14] analyzed consumer behavioral intentions toward Polyethylene Terephthalate (PET) recycling, suggesting that PET plastic waste recycling can address waste management challenges, support the circular economy, and protect the environment. Xia et al. [15] constructed a five-layer open-loop reverse logistics network model, including customers, collection, disassembly and inspection, remanufacturing, and disposal stages, to mitigate contradictions between rapid product growth and moderate recovery rates of end-of-life products.
In summary, most scholars have focused either on overall optimization or direct optimization in reverse logistics, with relatively few incorporating local optimization. The integration of both global and local optimization offers improved decision-making outcomes.
This study proposes a bi-level optimization model (global + local). To simplify the model, carbon tax is used as a parameter, converting carbon emission objectives into carbon emission costs. The dual-objective model is then transformed into a single-objective optimization problem. Under the constraints of the traditional global optimization model, a site-selection and routing local optimization model is introduced to better achieve low-carbon economic goals for reverse logistics networks. The effectiveness of the bi-level model is compared with that of a single-layer global optimization model to validate its advantages in making logistics networks more scientific, low-carbon, and economically viable, thereby aligning with national sustainability strategies.
3. Problem description
Under the dual-carbon goals of carbon neutrality and carbon peaking, the management of construction waste has become an unavoidable challenge. This study develops a construction waste classification and recycling logistics network, establishing two key nodes: landfill centers and resource recycling centers. The network design includes three candidate landfill center locations and five candidate resource recycling center locations, as illustrated in the diagram below (see Figure 1).
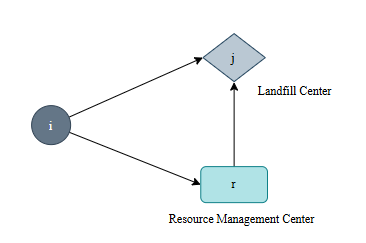
Figure 1. Classification of construction waste
3.1. Overall optimization model for the construction waste reverse logistics network
3.1.1. Parameter settings
3.1.1.1. Model parameters
\( I \) : Set of construction waste generation points, I= {i=1, 2, ..., n}
\( r \) : Set of resource recycling centers
\( j \) : Set of construction waste landfills
\( {Q_{i}} \) : Quantity of construction waste generated at point i per cycle
\( {a_{ir}} \) : Quantity of construction waste generated at point i per cycle
\( {a_{ij}} \) : Proportion of construction waste from source point transported to j
\( {a_{rj}} \) : Proportion of processed construction waste from resource center r transported to j
\( {F_{r}} \) : Construction cost of resource recycling center r
\( {F_{j}} \) : Construction cost of landfill r
\( {x_{ir}} \) : Quantity of waste transported from point i to recycling center r
\( {x_{ij}} \) : Quantity of waste transported from point i to landfill j
\( {x_{rj}} \) : Quantity of waste transported from recycling center r to landfill j
\( {Q_{r}} \) : Total quantity of waste received at recycling center r
\( {Q_{j}} \) : Total quantity of waste received at landfill j
\( {Q_{r}} \) : Quantity of construction waste received at recycling center r
\( {Q_{j}} \) : Quantity of construction waste received at landfill j
\( {D_{ir}} \) : Transportation distance per unit from waste generation point i to recycling center r
\( {D_{ij}} \) : Transportation distance per unit from waste generation point i to landfill j
\( {D_{rj}} \) : Transportation distance per unit from recycling center r to landfill j
\( {T_{ir}} \) : Transportation cost per unit from waste generation point i to recycling center r
\( {T_{ij}} \) : Transportation cost per unit from waste generation point i to landfill j
\( {T_{rj}} \) : Transportation cost per unit from recycling center r to landfill j
\( {P_{i}} \) : Classification processing cost per unit at waste generation point i
\( {P_{r}} \) : Processing cost per unit at recycling center r
\( {P_{j}} \) : Landfill disposal cost per unit at landfill j
\( {M_{r}} \) : Maximum processing capacity of recycling center r
\( {M_{j}} \) : Maximum processing capacity of landfill j
\( C{O_{2}} \) : Total carbon emissions
\( {C_{arbon-ys}} \) : Carbon emission factor per unit transport distance
\( {C_{arbon-yz}} \) : Carbon emission factor per unit operation of the recycling center
\( {C_{arbon-tm}} \) : Carbon emission factor per unit landfill disposal
\( γ \) : Carbon tax
\( m1 \) : Number of candidate landfill sites
\( m2 \) : Number of candidate recycling center sites
\( t1 \) : Number of landfills to be constructed
\( t2 \) : Number of recycling centers to be constructed
3.1.1.2. Decision variables
\( {y_{j}}=\begin{cases} \begin{array}{c} 1 set up a landfill center at j \\ 0 Do not set up a landfill center at j \end{array} \end{cases} \) | (1) |
\( {y_{r}}=\lbrace \begin{matrix}1 set up a resource recovery management center at r \\ 0 Do not set up a resource recovery management center at r \\ \end{matrix} \) | (2) |
\( {E_{ab}}=\lbrace \begin{matrix}1 Transport between a and b \\ 0 No transportation between a and b \\ \end{matrix} \) | (3) |
3.1.2. Cost objective analysis
(1) Fixed Costs
The fixed cost refers to the construction cost of recycling centers and landfills, including labor, materials, and machinery. The fixed cost function is defined as:
\( {F_{solid}}={F_{r}}{y_{r}}+{F_{j}}{y_{j}} \) | (4) |
(2) Construction Waste
Collection and Classification Costs
To enhance waste recycling efficiency and prevent contamination, source classification is necessary. The classification cost function is expressed as:
\( {C_{classify}}=\sum _{i∈I}{Q_{i}}{P_{i}} \) | (5) |
(3) Transportation Costs
Transportation costs include vehicle usage and fuel consumption costs, which are proportional to transportation distance. The transportation cost function is:
\( {C_{transportation}}=\sum _{i∈I}{D_{ir}}{T_{ir}}{X_{ir}}{E_{ir}}+\sum _{i∈I}{D_{ij}}{T_{ij}}{X_{ij}}{{E_{i}}_{j}}+{D_{rj}}{T_{rj}}{X_{rj}}{E_{rj}} \) | (6) |
(4) Recycling Processing Costs
Construction waste is transported to the resource management center, where different types of waste undergo classification and processing. In this model, the cost of resource processing refers to the expenses incurred by the resource management center in handling construction waste.
\( {C_{resoure}}=\sum _{i∈I}{P_{r}}{Q_{r}}{y_{r}} \) | (7) |
(5) Landfill Disposal Costs
After non-recyclable construction waste undergoes harmless treatment, it is transported to a construction waste landfill. In this model, the cost of resource processing also includes the expenses associated with landfill disposal of construction waste.
\( {C_{landfill}}=\sum _{i∈I}{P_{j}}{Q_{j}}{y_{j}} \) | (8) |
(6) Carbon Emission Costs
The carbon emission costs examined in this study consist of two main components: ① The carbon emission costs associated with the resource processing of recyclable construction waste and the harmless landfill disposal of non-recyclable construction waste; ② The carbon emission costs generated during the transportation process between various nodes.
①Carbon emissions from transportation:
\( {C_{YS}}=\sum _{i∈I}{C_{arbon-ys}}{D_{ir}}{X_{ir}}{E_{ir}}+\sum _{i∈I}{C_{arbon-ys}}{D_{ij}}{X_{ij}}{E_{ij}}+{C_{arbon-ys}}{D_{rj}}{X_{rj}}{E_{rj}} \) | (9) |
②Carbon emissions during the operational phase of the resource management center:
\( {C_{zy}}={C_{arbon-zy}}{Q_{r}}{y_{r}} \) | (10) |
③Carbon emissions during the landfill phase:
\( {C_{tm}}={C_{arbon-tm}}{Q_{j}}{y_{j}} \) | (11) |
④Total carbon emission cost calculation:
\( {f_{co2}}=γ({C_{YS}}+{C_{zy}}+{C_{tm}})=γ(\sum _{iϵI}{C_{arbon-ys}}{D_{ir}}{X_{ir}}{E_{ir}}+\sum _{iϵI}{C_{arbon-ys}}{D_{ij}}{X_{ij}}{E_{ij}} \) \( +{C_{arbon-ys}}{D_{rj}}{X_{rj}}{E_{rj}}+{C_{arbon-zy}}{Q_{r}}{y_{r}}+{C_{arbon-tm}}{Q_{j}}{y_{j}}) \) | (12) |
(7) Total Cost Function:
\( min{C_{sum}}={F_{solid}}+{C_{classify}}+{C_{transportation}}+{C_{resource}}+{C_{landfill}}+{f_{co2}} \) | (13) |
\( ={F_{r}}{y_{r}}+{F_{j}}{y_{j}}+\sum _{iϵI}{Q_{i}}{P_{i}}+\sum _{iϵI}{D_{ir}}{T_{ir}}{X_{ir}}{E_{ir}}+\sum _{iϵI}{D_{ij}}{T_{ij}}{X_{ij}}{E_{ij}} \) | (14) |
\( {D_{rj}}{T_{rj}}{X_{rj}}{E_{rj}}+\sum _{iϵI}{P_{r}}{Q_{r}}{y_{r}}+\sum _{iϵI}{P_{j}}{Q_{j}}{y_{j}}+γ(\sum _{iϵI}{C_{arbon-ys}}{D_{ir}}{X_{ir}}{E_{ir}} \) | (15) |
\( +\sum _{iϵI}{C_{arbon-ys}}{D_{ij}}{X_{ij}}{E_{ij}}+{C_{arbon-ys}}{D_{rj}}{X_{rj}}{E_{rj}} \) | (16) |
\( +{C_{arbon-zy}}{Q_{r}}{y_{r}}+{C_{arbon-tm}}{Q_{j}}{y_{j}}) \) | (17) |
3.1.3. Constraints
The constraints in this model are as follows:
\( {Q_{i}}{a_{ir}}={X_{ir}} \) | (18) |
\( {X_{ir}}={Q_{r}} \) | (19) |
\( {Q_{i}}{a_{ij}}={{X_{i}}_{j}} \) | (20) |
\( {Q_{r}}{a_{rj}}={X_{rj}} \) | (21) |
\( {X_{ij}}+{X_{rj}}={Q_{j}} \) | (22) |
\( {Q_{r}}≤{M_{r}} \) | (23) |
\( {Q_{j}}≤{M_{j}} \) | (23) |
\( {Q_{i}}≥0,{Q_{j}}≥0,{Q_{r}}≥0,{a_{ij}}≥0,{a_{ir}}≥0,{a_{rj}}≥0; \) \( {X_{ir}}≥0,{X_{ij}}≥0,{X_{ir}}≥0,{X_{rj}}≥0; \) | (24) |
Constraints (18) and (19) ensure the balance between collection and transportation for the waste sent to the resource management center; Constraints (20) and (21) ensure the balance between collection and transportation for the waste sent to the landfill center; Constraint (22) ensures that the amount of construction waste sent to the resource management center does not exceed its maximum processing capacity; Constraint (23) ensures that the amount of construction waste sent to the landfill center does not exceed its maximum capacity; Constraint (24) enforces the non-negativity of parameters.
3.2. Location-path optimization model for the reverse logistics network of construction waste
Under the constraints of the overall optimization model, the objective is to minimize costs (both economic and environmental) while making decisions on the location and construction of landfill centers and resource management centers, as well as the selection of transportation routes between facilities. A location-path local optimization model is incorporated to better achieve the goal of a low-carbon and cost-efficient logistics network, verifying the effectiveness of the dual-layer overall + local model.
3.2.1. Location optimization of the reverse logistics network for construction waste
The siting of landfill centers is a key component in the classification, processing, and recycling of construction waste within the reverse logistics network. The critical decision for resource recovery enterprises is how to select the locations of landfill centers and resource management centers in a cost-effective manner. The node location problem aims to determine the optimal locations within a predefined area that can accommodate construction waste generated at various points while minimizing transportation costs.
To simplify the problem, the following assumptions are made:
①Landfill centers and resource management centers can only be selected from a given set of candidate locations;
②Transportation costs are proportional to the amount of waste transported;
③The capacities of landfill centers and resource management centers are sufficiently large to meet all demands;
④The demand at each waste generation point is known.
Assuming there are n construction waste generation points with known waste production levels, the objective is to select t distribution centers from m candidate locations to minimize the total cost of the distribution system.
3.2.1.1. Decision variables
The decision variables in the local site selection optimization model are consistent with those in the overall optimization model. The goal is to select landfill center and resource management center locations strategically to reduce costs.
\( {y_{j}}=\lbrace \begin{matrix}1 set up a landfill center atj \\ 0 Do not set up a landfill center atj \\ \end{matrix} \) | (25) |
\( {y_{r}}=\lbrace \begin{matrix}1 set up a resource recovery management center at r \\ 0 Do not set up a resource recovery management center at r \\ \end{matrix} \) | (26) |
3.2.1.2. Model formulation
The objective function of the model aims to minimize the total cost, which consists of two components: The first term represents the total transportation cost from construction waste generation points to processing sites; The second term represents the fixed costs of the processing sites.
Since construction waste is categorized and processed separately, the site selection model consists of two parts:
①Landfill Center Location Model
\( min{z}=\sum _{j=1}^{m1}\sum _{i=1}^{n}{x_{ij}}{T_{ij}}+\sum _{j=1}^{m1}{y_{j}}{F_{j}} \) | (27) |
s.t | |
\( \sum _{j=1}^{m1}{x_{ij}}={a_{ij}}{Q_{i}},i=1,2,......,n \) | (28) |
\( \sum _{j=1}^{m1}{y_{j}}={t_{1}} \) | (29) |
\( \sum _{i=1}^{n}{x_{ij}}≤M{y_{j}},j=1,2,...,{m_{1}} \) | (30) |
\( {x_{ij}}≥0,{y_{j}}=0,1;\begin{matrix} \\ \end{matrix}i=1,2......n;j=1,2......{m_{1}} \) | (31) |
Equation (28) ensures the balance between collection and transportation of construction waste from generation points to landfill centers; Equation (29) restricts the number of planned landfill centers to one; Equation (30) ensures that the amount of waste transported to the landfill center does not exceed its maximum capacity; Equation (31) enforces non-negativity constraints.
②Resource Management Center Location Model
\( min{z}=\sum _{r=1}^{m2}\sum _{i=1}^{n}{x_{ir}}{T_{ir}}+\sum _{r=1}^{m2}{y_{r}}{F_{r}} \) | (32) |
s.t | |
\( \sum _{r=1}^{m2}{x_{ir}}={a_{ir}}{Q_{i}},i=1,2,......,n \) | (33) |
\( \sum _{r=1}^{m2}{y_{r}}={t_{2}} \) | (34) |
\( \sum _{i=1}^{n}{x_{ir}}≤M{y_{r}},r=1,2......{m_{2}} \) | (35) |
\( {x_{ir}}≥0,{y_{r}}=0,1;\begin{matrix} \\ \end{matrix}i=1,2......n;r=1,2......{m_{2}} \) | (36) |
Equation (33) ensures the balance between collection and transportation of construction waste from generation points to resource management centers; Equation (34) restricts the number of planned resource management centers to one; Equation (35) ensures that the amount of waste transported to the resource management center does not exceed its maximum capacity; Equation (36) enforces non-negativity constraints.
3.2.2. Transportation route optimization for the reverse logistics network of construction waste
This study defines logistics route planning within the designed reverse recycling network by considering source separation at waste generation points. Construction waste is categorized into recyclable and non-recyclable waste, which are transported separately to landfills and resource management centers, respectively. To enhance the effectiveness of source separation, two independent fleets are used to collect recyclable and non-recyclable waste without interference.
The study involves two collection points, n waste generation points, and k vehicles. The objective is to determine the optimal vehicle routes that traverse all waste generation points while meeting collection requirements, ensuring the minimum total travel distance. The construction waste collection route diagram is shown in Figure 2.

Figure 2. Construction waste recycling pathway model construction
To simplify the problem, we first make the following assumptions:
①The coordinates of the landfill centers, resource management centers, and waste generation points are known;
②The waste volume at each generation point is known and does not exceed the standard load capacity of a single vehicle;
③Each waste generation point must be serviced exactly once by a single vehicle;
④Road conditions do not impact vehicle travel distances;
⑤The vehicle fleet at the collection center consists of identical vehicles with sufficient numbers, and each collection trip does not exceed the vehicle’s maximum driving range;
⑥The capacity of the collection center is sufficiently large.
3.2.2.1. Parameter settings
①Basic Parameters
Based on research needs, the problem is formulated as a directed graph G= {V, A}, where V consists of two parts: V= {0} represents either the landfill or the resource management center, V= {1,2…m} represents various construction waste generation points. The arc sets are defined as follows: Aj={(i,j)|i,j∈V,i≠j} represents transportation arcs to the landfill. Ar={(i,r)|i,r∈V,i≠r} represents transportation arcs to the resource management center.
②Decision Variables
\( x_{ir}^{k}=\lbrace _{0 \begin{matrix}Others & & & & \\ \end{matrix}}^{1 The vehicle numbered K transports from i to r} \) | (37) |
\( x_{ij}^{k}=\lbrace _{0\begin{matrix} Others & & & & \\ \end{matrix}}^{1 The vehicle numbered K transports from i to r} \) | (38) |
\( y_{i}^{k}=\lbrace _{0 Others}^{1 The vehicle numbered K picks up goods from i} \) | (39) |
3.2.2.2. Model formulation
The objective of the model is to minimize the total collection distance, which consists of the collection distances for recyclable waste and non-recyclable waste.
\( min{D}=\sum _{i∈V}\sum _{j∈V,i \lt j}\sum _{k∈K}{D_{ij}}x_{ij}^{k}+\sum _{i∈V}\sum _{r∈V,r \lt j}\sum _{k∈K}{D_{ir}}x_{ir}^{k} \) | (40) |
s.t | |
\( \sum _{i∈V}{x_{ij}}x_{ij}^{k}{b_{ik}}≤M \) | (41) |
\( \sum _{i∈V}{x_{ir}}x_{ir}^{k}{b_{ik}}≤M \) | (42) |
\( \sum _{k}{b_{ik}}=1,i∈V,k∈K \) | (43) |
\( \sum _{i∈V}x_{ij}^{k}=y_{i}^{k} \) | (44) |
\( \sum _{i∈V}x_{ir}^{k}=y_{i}^{k} \) | (45) |
Equation (40): Represents the objective function, optimizing the total transportation distance for construction waste collection; Constraint (41): Restricts the vehicle load capacity for transporting non-recyclable waste; Constraint (42): Restricts the vehicle load capacity for transporting recyclable waste; Constraint (43): Ensures that each waste generation point is serviced exactly once; Constraint (44): Ensures that vehicles depart from the landfill center; Constraint (45): Ensures that vehicles depart from the resource management center.
4. Algorithm design
The Simulated Annealing (SA) Algorithm is inspired by the annealing process in solid materials and its similarities with combinatorial optimization problems. Starting from a high initial temperature, the algorithm gradually reduces the temperature parameter while incorporating a probabilistic jump mechanism to explore the solution space in search of the global optimal solution.
Simulated annealing assigns a time-dependent probability mechanism that eventually approaches zero, allowing it to effectively avoid getting trapped in local minima and ensuring convergence to the global optimum. It has strong local search capabilities and high iterative search efficiency, with a certain probability of accepting inferior solutions compared to the current one. This helps prevent premature convergence, allows the search to escape local optima, and enhances robustness by ensuring that the final solution is independent of the initial state. Additionally, SA improves computational efficiency.
5. Case study
5.1. Case data
5.1.0.1. Construction waste generation
The annual construction waste output at each waste generation point is estimated based on the construction scale, completed building area, and demolition area data published on the official website of District X.
5.1.0.2. Transportation distance from waste generation points to candidate sites
The distance from each construction waste generation point in District X to the landfill center and resource management center candidate sites is measured using map-based calculations.
5.1.0.3. Other relevant parameters
Carbon tax price is set at 0.056 RMB/kg, based on data from carbon emission trading institutions; Carbon emissions during transportation are primarily related to fuel consumption of transport vehicles; Carbon emissions during resource processing are mainly caused by electricity usage; Fixed unit costs refer to the construction costs of candidate sites, amortized over the study period.
Additional parameter settings are listed in Table 1:
Table 1. Parameter Settings
Parameter Type | Parameter | Value |
Carbon Emissions | Heavy-duty gasoline truck(15t) | 0.104 kg/(t.km) |
Carbon emissions from electricity(1kwh) | 0.96kg/t | |
Construction waste landfill emissions | 3.7kg/t | |
Carbon tax rate | 0.056 yuan/kg |
5.2. Results analysis
The proposed optimization model was solved using mathematical analysis software and the Simulated Annealing Algorithm. The final computational results confirmed the effectiveness of the local optimization model.
6. Conclusion
To support sustainable development, this study develops an optimization model for the reverse logistics network of construction waste recycling, incorporating cost efficiency and environmental benefits as dual objectives. A global-local optimization model is proposed to solve the logistics network problem. Through comparative analysis of model data, it is demonstrated that whether considering economic costs or carbon emission costs, the global-local bi-level optimization model offers distinct advantages. The results confirm the effectiveness of integrating local optimization within a global optimization framework, providing strategic insights for national construction waste recycling and offering practical significance for sustainable waste management.
References
[1]. Li, H. X. (2018). Design of reverse logistics network and recycling game analysis for construction waste based on multi-objective optimization (Doctoral dissertation, Zhejiang Gongshang University).
[2]. Li, X. P., Cai, D., Guo, C. X., et al. (2019). Design of a construction waste reduction system logistics network from a multidimensional perspective. Systems Engineering—Theory & Practice, 39(11), 2842–2854.
[3]. Xueqing Z, Rabnawaz R A. (2022). A queuing system for inert construction waste management on a reverse logistics network. Automation in Construction, 137.
[4]. Vargas B D, Campos S D M L, Luna M M M. (2023). Brazil’s Formal E-Waste Recycling System: From Disposal to Reverse Manufacturing. Sustainability, 16(1).
[5]. Karthik B, Aditya K, Saket S, et al. (2024). Blockchain technology: a catalyst for reverse logistics of the automobile industry. Smart and Sustainable Built Environment, 13(1), 133-178.
[6]. Chu, D. L., Fan, X., Dou, X. F., et al. (2023). Research on the reverse logistics recycling network system based on "Internet + TPR". Packaging Engineering, 44(11), 166–174. https://doi.org/10.19554/j.cnki.1001-3563.2023.11.019
[7]. Mao, T. (2023). Preliminary exploration of the construction of a green logistics system in China's manufacturing industry—From the perspective of carbon peaking and carbon neutrality. Environmental Protection, 51(Z2), 10–13. https://doi.org/10.14026/j.cnki.0253-9705.2023.z2.003
[8]. Hajar R. (2024). The Contribution of Reverse Logistics Practices in Circular Economy Principles: A TOWS Analysis. IFAC PapersOnLine, 58(13), 733-738.
[9]. Barimah F A. (2024). Analyzing the implementation of reverse logistics in the Accra metropolis plastic waste management. Journal of Material Cycles and Waste Management, (prepublish), 1-18.
[10]. Subhodeep M, Ramji N, K. M, et al. (2024). Artificial intelligence-based reverse logistics for improving circular economy performance: a developing country perspective. The International Journal of Logistics Management, 35(6), 1779-1806.
[11]. Jauhar K S, Singh A, Kamble S, et al. (2024). Reverse logistics for electric vehicles under uncertainty: An intelligent emergency management approach. Transportation Research Part E, 192, 103806-103806.
[12]. Perez P Y, Rojas M, Mier A R. (2024). Design of a reverse logistics network for medical waste considering location and routing decisions. Journal of Cleaner Production, 474, 143592-143592.
[13]. Sorichetti E A, Prieto G M, Savoretti A A, et al. (2024). Reverse logistics for empty pesticide containers: optimal design for sustainable management over wide areas. Environment, Development and Sustainability, (prepublish), 1-31.
[14]. Farida Y, Siswanto N, Vanany I. (2024). Reverse logistics toward a circular economy: Consumer behavioral intention toward polyethylene terephthalate (PET) recycling in Indonesia. Case Studies in Chemical and Environmental Engineering, 101008, 07-07.
[15]. Xia H, Chen Z, Syed M J, et al. (2024). Uncertain programming model for designing multi-objective reverse logistics networks. Cleaner Logistics and Supply Chain, 11, 100155-.
Cite this article
Xie,H.;Li,C. (2025). Dual layer optimization of construction waste classification treatment and recycling logistics network. Advances in Engineering Innovation,16(2),61-70.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Journal:Advances in Engineering Innovation
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Li, H. X. (2018). Design of reverse logistics network and recycling game analysis for construction waste based on multi-objective optimization (Doctoral dissertation, Zhejiang Gongshang University).
[2]. Li, X. P., Cai, D., Guo, C. X., et al. (2019). Design of a construction waste reduction system logistics network from a multidimensional perspective. Systems Engineering—Theory & Practice, 39(11), 2842–2854.
[3]. Xueqing Z, Rabnawaz R A. (2022). A queuing system for inert construction waste management on a reverse logistics network. Automation in Construction, 137.
[4]. Vargas B D, Campos S D M L, Luna M M M. (2023). Brazil’s Formal E-Waste Recycling System: From Disposal to Reverse Manufacturing. Sustainability, 16(1).
[5]. Karthik B, Aditya K, Saket S, et al. (2024). Blockchain technology: a catalyst for reverse logistics of the automobile industry. Smart and Sustainable Built Environment, 13(1), 133-178.
[6]. Chu, D. L., Fan, X., Dou, X. F., et al. (2023). Research on the reverse logistics recycling network system based on "Internet + TPR". Packaging Engineering, 44(11), 166–174. https://doi.org/10.19554/j.cnki.1001-3563.2023.11.019
[7]. Mao, T. (2023). Preliminary exploration of the construction of a green logistics system in China's manufacturing industry—From the perspective of carbon peaking and carbon neutrality. Environmental Protection, 51(Z2), 10–13. https://doi.org/10.14026/j.cnki.0253-9705.2023.z2.003
[8]. Hajar R. (2024). The Contribution of Reverse Logistics Practices in Circular Economy Principles: A TOWS Analysis. IFAC PapersOnLine, 58(13), 733-738.
[9]. Barimah F A. (2024). Analyzing the implementation of reverse logistics in the Accra metropolis plastic waste management. Journal of Material Cycles and Waste Management, (prepublish), 1-18.
[10]. Subhodeep M, Ramji N, K. M, et al. (2024). Artificial intelligence-based reverse logistics for improving circular economy performance: a developing country perspective. The International Journal of Logistics Management, 35(6), 1779-1806.
[11]. Jauhar K S, Singh A, Kamble S, et al. (2024). Reverse logistics for electric vehicles under uncertainty: An intelligent emergency management approach. Transportation Research Part E, 192, 103806-103806.
[12]. Perez P Y, Rojas M, Mier A R. (2024). Design of a reverse logistics network for medical waste considering location and routing decisions. Journal of Cleaner Production, 474, 143592-143592.
[13]. Sorichetti E A, Prieto G M, Savoretti A A, et al. (2024). Reverse logistics for empty pesticide containers: optimal design for sustainable management over wide areas. Environment, Development and Sustainability, (prepublish), 1-31.
[14]. Farida Y, Siswanto N, Vanany I. (2024). Reverse logistics toward a circular economy: Consumer behavioral intention toward polyethylene terephthalate (PET) recycling in Indonesia. Case Studies in Chemical and Environmental Engineering, 101008, 07-07.
[15]. Xia H, Chen Z, Syed M J, et al. (2024). Uncertain programming model for designing multi-objective reverse logistics networks. Cleaner Logistics and Supply Chain, 11, 100155-.









