1. Introduction

In recent years, the Chinese government has issued multiple policy documents promoting prefabricated construction [1]. As a core vehicle for the industrial transformation of the construction industry, prefabricated buildings are characterized by “heavy components, high-altitude operations, and complex multi-trade coordination” in hoisting operations [2]. China has now entered a stage of high-quality development in prefabricated construction [3]. According to the 2023 Construction Safety Report released by the Ministry of Housing and Urban-Rural Development, hoisting accidents account for 63.5% of all accidents in prefabricated construction projects. Among these, 75% are attributed to delays in risk warnings, making this a key bottleneck restricting industry development.

As a critical stage of construction, hoisting operations exhibit multi-dimensional risk coupling. The challenges arise from dynamic high-altitude environments, high-load equipment operation, and complex human-machine interactions. The existing “manual inspection + static rules” safety management system lacks real-time responsiveness and precision. With the implementation of the 14th Five-Year Plan for the Intelligentization of the Construction Industry, intelligent early warning systems integrating the Internet of Things (IoT), edge computing, and machine learning have emerged as a breakthrough direction. In terms of construction safety management for prefabricated buildings, earlier domestic and international research focused on traditional qualitative and quantitative assessments, establishing safety risk levels and indicator systems during construction processes [4-9]. As the industry transitions toward intelligentization, safety management has shifted toward research on complex coupled models [10-17]. However, these safety management approaches remain primarily at a macro level, with limited studies targeting specific construction activities. To minimize the occurrence of safety incidents, it is essential to develop safety management methods specifically for hoisting operations. Both domestic and international scholars have made some progress in this area. Safety risk management research is gradually evolving from static evaluations to dynamic intelligent analyses, showing an increasing trend of interdisciplinary integration. For example, Jiang [18] systematically identified 16 core risk factors in prefabricated hoisting operations using the Delphi method and classified risk levels based on the Fuzzy Analytic Hierarchy Process (FAHP). However, its weight assignment still relies on expert judgment, introducing subjective bias. Li [19] further applied an improved DEMATEL-OWA hybrid method, analyzing risk evolution paths through causal diagrams and identifying “excessive equipment vibration” and “operator fatigue” as key coupling factors. Nevertheless, its dynamic adaptability remains to be validated. To address the variability and uncertainty in hoisting processes, Yang [20] developed a Dynamic Bayesian Network (DBN) model, which updates node probabilities based on time-series data to enable real-time risk inference, though it suffers from high computational complexity. Xu [21] used an improved Mask R-CNN algorithm to identify unsafe behaviors such as workers not wearing safety harnesses, achieving an accuracy rate of 91.5%. However, the model’s dependence on GPU computing power limits its application in edge deployment scenarios. Liu et al. [22] were the first to introduce Relevance Vector Machines (RVM) into hoisting safety early warning systems. Based on a Bayesian framework, they achieved small-sample risk prediction, but the feature engineering process still depends on expert knowledge. Subsequently, Liu et al. [23] constructed a risk management framework for hoisting operations and developed a risk coupling model. By integrating IoT technology, Building Information Modeling (BIM), and the Apriori algorithm for safety risk analysis, they realized visual management. Their analysis of correlations among various risk factors in hoisting operations improved information integration efficiency, filled the research gap in risk factor coupling analysis, and enabled effective safety management and decision-making. Sun et al. [24] used questionnaires and accident data to improve the traditional Human Factors Analysis and Classification System (HFACS), developing the HFACS-Prefabricated Hoisting (PH) risk model. Combined with factor analysis based on Structural Equation Modeling (SEM), they established a comprehensive safety prevention and control system for the hoisting process of prefabricated components. Huang [25] proposed a GA-SVM-based safety early warning model for hoisting operations, integrating Genetic Algorithms with Support Vector Machines to improve classification accuracy and extend SVM’s binary classification to multi-class classification. It is evident that current research on the safety management of prefabricated hoisting operations mostly focuses on accident causes and influencing factor identification, with limited research on safety early warning systems. Although existing hoisting safety indicator systems are relatively mature and have promoted the development of safety early warning methods, there is still room for improvement. For example, there are many indicators influencing unsafe hoisting behaviors, often involving complex nonlinear relationships. Directly using these factors affects the prediction accuracy of early warning models. While SVM performs well in nonlinear fitting, it is easily affected by redundant information, reducing the accuracy of early warning models.

To address these issues, this study proposes a collaborative optimization model that integrates Random Forest (RF), Genetic Algorithm (GA), and Support Vector Machine (SVM), referred to as RF-GA-SVM. Based on the analysis of unsafe behavior indicators in prefabricated building hoisting operations, the RF algorithm is used for feature importance analysis to rank independent variables. The top-ranked variables are then selected as inputs for the GA-SVM model. A case study is conducted to validate the feasibility of the method, providing a reference for improving the safety management of hoisting operations in prefabricated construction.

2. Methodology of the RF-GA-SVM-based early warning model

2.1. Early warning indicator selection based on RF

2.1.1. Random forest

Random Forest (RF), due to its inherent capability for feature importance evaluation [26], is widely used for indicator reduction in high-dimensional data. Its core principle is to quantify the contribution of each feature to classification outcomes by employing the Gini Index or Permutation Importance. This facilitates the elimination of redundant features and enhances the model’s generalization ability. In this study, the Random Forest (RF) algorithm is applied to screen early warning indicators from the initial sample set of unsafe behaviors in prefabricated building hoisting operations. The purity of the sample set is represented by the Gini Index, calculated as follows:

\( Gini({X_{i}})=1-\sum _{k=1}^{K} {(\frac{{N_{k}}}{N})^{2}}\ \ \ (1) \)

Where: \( {N_{k}} \) is the number of samples of class k at the node; \( N \) is the total number of samples at the node. The smaller the Gini Index, the higher the purity of the child nodes after the feature split, indicating a greater contribution of the feature to classification.

The specific steps for feature indicator selection are shown in Figure 1.

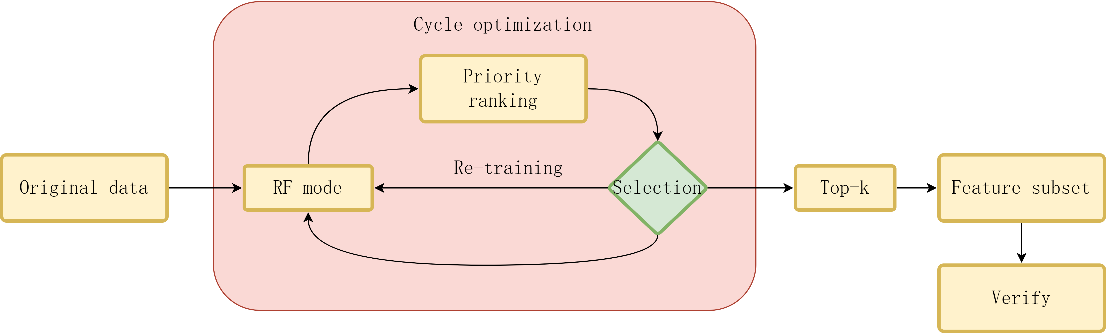
Figure 1. RF feature selection process

2.1.2. Establishment of the early warning indicator system

In prefabricated building hoisting operations, safety accidents are often triggered by the dynamic coupling of multiple factors. The “4M” theoretical framework categorizes accident causes into a four-dimensional dynamic coupling system comprising “Man-Machine-Environment-Management.” Based on a comprehensive review of the literature, analysis of causal chains in tower crane accident cases in prefabricated buildings, and relevant regulations, this study ultimately develops an indicator system that includes 4 primary indicators and 25 secondary indicators. The initial selection of the safety early warning indicator system for hoisting operations in prefabricated buildings is shown in Table 1.

Table 1. Initial selection of safety warning indicators for hoisting operations in prefabricated buildings

2.2. SVM model based on GA parameter optimization

2.2.1. Principle of SVM

Support Vector Machine (SVM) achieves classification in high-dimensional space by identifying an optimal hyperplane. Its performance depends on the parameters of the kernel function (such as γ in the RBF kernel) and the penalty factor C. The concept was first proposed by Vapnik [27]. The computational steps adopted in this study are as follows:

1) Design the Training Set: Let the number of training samples be l, and the training samples be \( T=\lbrace ({x_{1}},{y_{1}}),⋯,({x_{i}},yi)\rbrace ∈T=\lbrace ({x_{1}},{y_{1}}),…,({x_{i}},{y_{i}})\rbrace {∈(X×Y)^{l}} \) . The expression for the hyperplane is:

\( f(x)={w^{T}}φ({x_{i}})+b\ \ \ (2) \)

Where: w denotes the weight vector, b is the bias term, and \( φ({x_{i}}) \) is an unknown nonlinear mapping function.

2) Introduce Slack Variables and Penalty Function: Since not all data are linearly separable, a slack variable \( {ξ_{i}} \) and a penalty function C>0 are introduced. The mathematical formulation becomes the following convex quadratic programming problem, as shown in the equation below:

\( \begin{cases} \begin{array}{c} \underset{w,b,ξ}{min} \frac{1}{2}∥w{∥^{2}}+C\sum _{i=1}^{l} {ξ_{i}} \\ {y_{i}}{w^{T}}φ({x_{i}})+b≥1-{ξ_{i}},∀i=1,2,…,m \end{array} \end{cases}\ \ \ (3) \)

Where: \( {y_{i}} \) is the sample label, and \( {x_{i}} \) is the input vector of the sample.

3) Introduce Lagrange Multipliers and Kernel Function: By applying the Lagrange multiplier method (Lagrangian function), the original problem is transformed into its dual form, and a kernel function \( K({x_{i}},{x_{j}}) \) is introduced to handle nonlinear feature mapping, as shown in the equation below:

\( \begin{cases} \begin{array}{c} \underset{a}{max} \sum _{i=1}^{l} {α_{i}}-\frac{1}{2}\sum _{i,j=1}^{n} {α_{i}}{α_{j}}{y_{i}}{y_{j}}K({x_{i}},{x_{j}}) \\ 0≤{α_{i}}≤C, \sum _{i=1}^{n} {α_{i}}{y_{i}}=0 \end{array} \end{cases}\ \ \ （4） \)

Where: \( {α_{i}},{α_{j}} \) is the Lagrange multiplier.

Given the nonlinear characteristics of the hoisting behavior data, the Gaussian Radial Basis Function (RBF) kernel is selected, with its expression shown as:

\( K({x_{i}},{x_{j}})=exp{(-\frac{∥{x_{i}},{x_{j}}{∥^{2}}}{2{σ^{2}}})}\ \ \ (5) \)

Where: \( σ \) is the radius of the radial basis function.

4) Construct the Decision Function: For the early warning of unsafe hoisting behavior, four risk levels are classified (safe, low risk, medium risk, and high risk). The One-vs-Rest (OvR) strategy is adopted. The SVM classification function based on RBF is shown in the equation below:

\( f(x)=\sum _{i=1}^{l} {α_{i}}{y_{i}}K({x_{i}},x)+b\ \ \ （6） \)

2.2.2. GA-based optimization of SVM

The generalization performance and prediction accuracy of SVM highly depend on the coordinated optimization of the penalty factor C and the radial basis kernel parameter γ [28]. Traditional parameter optimization methods have two major limitations: First, experience-driven parameter combinations are prone to local optima. Second, exhaustive searches in high-dimensional parameter spaces result in low computational efficiency. To address the above issues, this study establishes an adaptive SVM parameter optimization model using the Genetic Algorithm (GA).

The Genetic Algorithm (GA) is a global optimization algorithm that simulates the process of biological evolution. It searches for the optimal solution in the solution space through selection, crossover, and mutation operations. By simulating the biological evolution mechanism, it efficiently finds the optimal combination of penalty factor C and kernel parameter γ, avoiding the randomness of manual parameter tuning. The implementation process can be divided into the following steps [29]:

1) Real-Number Encoding: Map C and γ to chromosome individuals using real-number encoding, set the parameter search range based on experience, and randomly generate the initial population.

2) Fitness Function Design: Design a fitness function centered on cross-validation accuracy or weighted recall rate to quantify the quality of individuals, with higher weights assigned to high-risk categories in engineering safety scenarios.

3) Simulate Gene Recombination and Mutation: Select and retain high-quality individuals. Combine arithmetic crossover and non-uniform mutation operations to balance global exploration and local exploitation capabilities. Dynamically adjust the search step size to avoid premature convergence.

4) Output Optimal Parameters: Output the optimal parameters when the maximum number of iterations or fitness stability threshold is met.

2.3. Model evaluation metrics

To evaluate the performance of the classification model developed in this study, the confusion matrix method was adopted. First, the confusion matrix is a fundamental tool in classification problems, used to illustrate the relationship between actual classes and predicted classes. Since the early warning model established in this study involves a four-class classification problem, the confusion matrix takes the form of a 4×4 matrix. The diagonal elements represent the number of correctly classified samples, while the off-diagonal elements indicate misclassifications. Traditional metrics such as Accuracy, Precision, Recall, and F1-Score may not fully capture all performance details, particularly in the case of class imbalance. Therefore, it is necessary to calculate performance metrics for each class individually and conduct a comprehensive evaluation through Macro-Average and Weighted-Average methods. The processed confusion matrix is shown in Table 2.

Table 2. Four-class confusion matrix

Regardless of the number of classes, Accuracy represents the proportion of correctly predicted samples out of the total number of samples. This calculation remains consistent in both multi-class and binary classifications and does not require further adjustment. However, Precision and Recall must be calculated individually for each class in multi-class classifications. The confusion matrix must fi4rst be constructed, which provides a detailed view of each class’s prediction performance. The diagonal elements of the confusion matrix indicate the number of correctly predicted samples for each class. The other elements in each row show the number of samples from that class misclassified as other classes, while the other elements in each column indicate the number of samples incorrectly predicted as belonging to that class. Based on the confusion matrix, Precision and Recall for each class can be calculated. Precision is the proportion of correctly predicted samples for a given class out of all samples predicted to belong to that class. Recall is the proportion of correctly predicted samples for a given class out of all actual samples of that class.

3. Case analysis

3.1. Data preparation

The real-time monitoring values of various indicators are used as input variables, while the safety early warning levels for hoisting operations serve as output variables. The early warning levels are defined as P = (No Warning, Minor Warning, Moderate Warning, Severe Warning), corresponding to the category vector R = (1, 2, 3, 4). A total of 400 data samples were selected from accident case mining as the original training dataset. A portion of the data is shown in Table 3.

Table 3. Safety early warning indicators for hoisting operations (partial dataset)

3.2. Feature selection of early warning indicators based on RF

Using MATLAB 2024a software, the Random Forest (RF) model was applied to calculate and rank the importance of each feature. First, the dataset was imported and split into a training set and a test set with a ratio of 9:1 [25]. The number of decision trees was set to 300, and the minimum number of samples for leaf nodes was set to 5. Feature importance was then computed. After running the iterations and training the model, the importance scores of 25 early warning indicators were obtained, as shown in Figure 2.

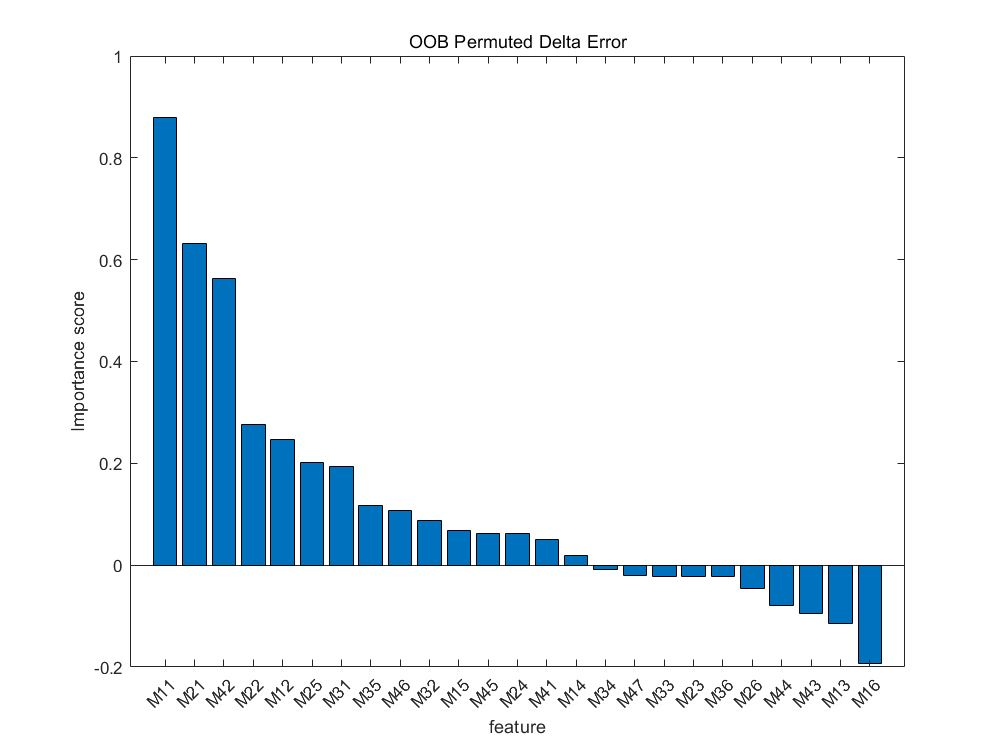
Figure 2. Importance distribution of safety early warning indicators for hoisting operations

As shown in Figure 2, ten indicators—M34, M47, M33, M23, M36, etc.—had negative values and were identified as interference factors. After removing these ten indicators, a final set of 15 indicators was determined, as listed in Table 4.

Table 4. The 15 most important early warning indicators

3.3. GA-SVM parameter optimization

After selecting the feature indicators using the RF method described earlier, the 15 selected early warning indicators are used as input variables for the early warning model, with the warning level as the output variable. Utilizing the MATLAB R2024a software platform, a GA-SVM code model was developed to optimize the parameters of the hoisting operation safety early warning model. The initial parameter settings are as follows: the penalty parameter C is set within the range [0.1, 100]; the crossover probability is set to 0.6; the kernel function parameter g is set within the range [0.01, 1000]; and the mutation probability is set to 0.1. A 3-fold cross-validation method is adopted for parameter optimization, while all other parameters remain at their default values. The dataset is then imported for parameter tuning, and the resulting fitness curve is shown in Figure 3.

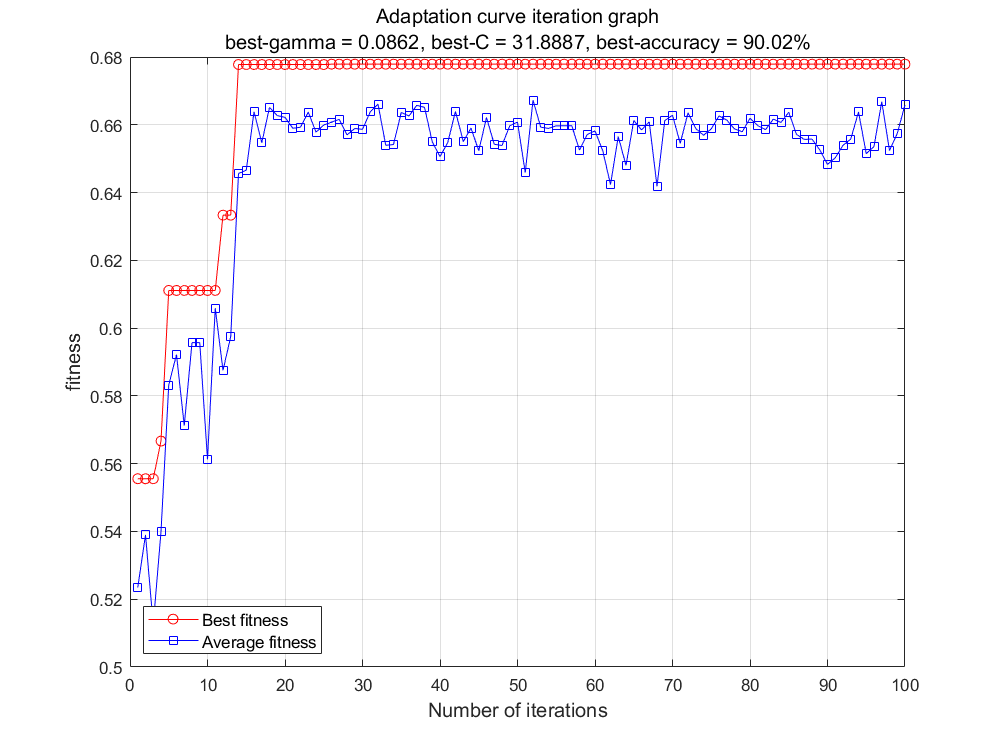
Figure 3. Optimal fitness curve for GA-SVM model parameter tuning

As illustrated in Figure 3, the fitness value shows a steep increase in the early iterations, indicating that the GA effectively explored the parameter space. Although the curve tends to stabilize multiple times during the early iterations, it levels off prematurely before the fitness value reaches the expected level. Ultimately, the curve stabilizes after approximately 20 iterations, resulting in the optimal parameters for the SVM model \( C=31.887,g=0.0862 \) .

3.4. Model evaluation

To validate the effectiveness of the model, the optimal parameters obtained are substituted into the SVM model and compared with the traditional SVM model. The confusion matrices before and after optimization are shown in Figure 4 and 5, respectively.

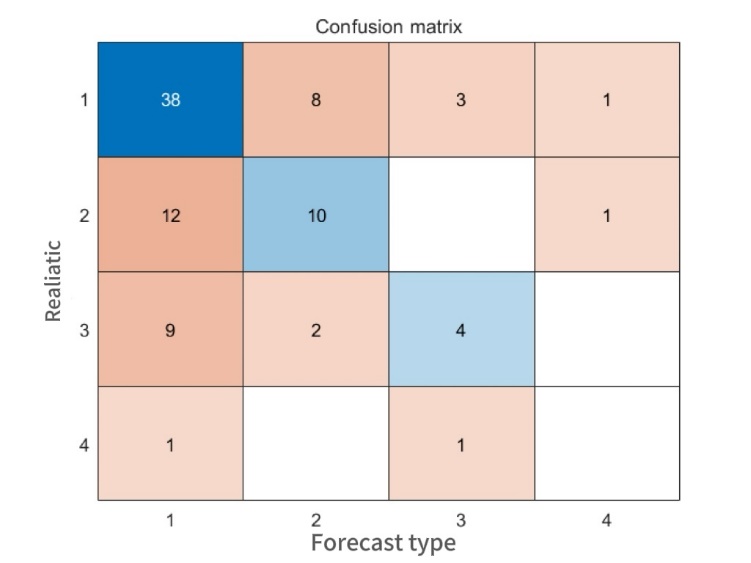
Figure 4. Confusion matrix before optimization

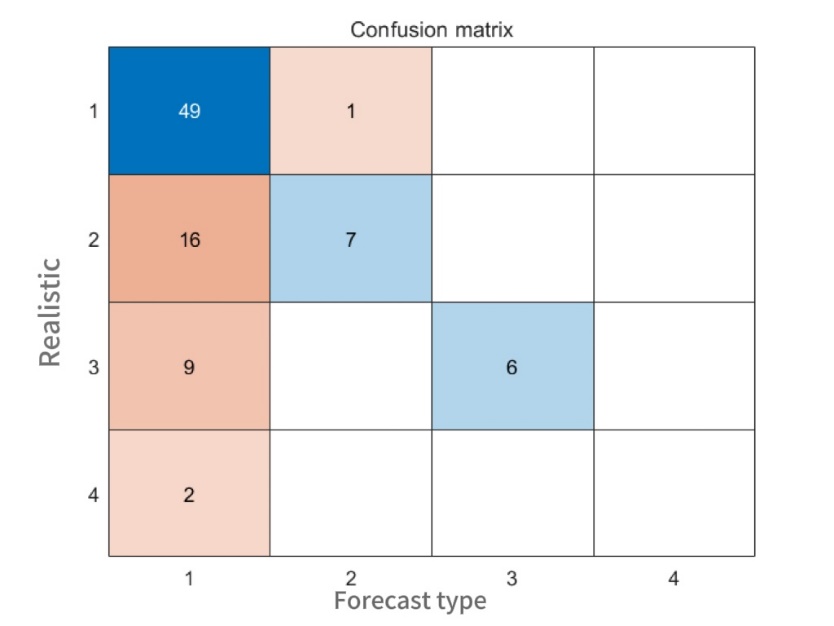
Figure 5. Optimized confusion matrix

By comparing the two figures, it is evident that the final RF-GA-SVM model demonstrates superior performance in feature selection, parameter optimization, and classification capabilities. Compared with the traditional SVM model, the proposed model improves the overall classification accuracy by 11 cases, indicating an enhancement in predictive performance to a certain extent. Therefore, the RF-GA-SVM early warning model proposed in this study is feasible and provides a valuable reference for the safety management of prefabricated hoisting operations.

4. Conclusion

Using the RF algorithm, 20 highly significant indicators were selected, such as the tower crane operator’s real-time fatigue index, brake wear degree, and the probability of wire rope fracture, while excluding other potentially less important indicators. These were used as the independent variables for the RF-GA-SVM model. The results indicate that the early warning accuracy improved after RF-based feature selection.

The RF-GA-SVM model randomly selected test samples. By comparing the results with those of the GA-SVM and traditional SVM models, it was found that the classification accuracy increased by 11 cases, verifying the higher accuracy of this model in early warning classification.