1. Introduction

Qingdao Jiaodong International Airport [1, 2] has pioneered the integration of aviation, high-speed rail, and urban rail transit systems, achieving a seamless vertical connection with zero transfers, becoming the first such transportation hub in China. Through innovations such as establishing urban terminals and piloting high-speed rail ticket exemptions, it has initially formed an “air-rail integration” intermodal transport model. However, its ticketing services still face two main bottlenecks: first, the lack of diverse product offerings resulting in insufficient customer group coverage; second, the need for breakthroughs in differentiated pricing and sustainable service models. Existing research on air-rail intermodal ticketing optimization mostly focuses on macro-level aspects. For example, Gang et al. [3] proposed standards for multi-transport mode ticket information sharing interfaces, Hui et al. [4] constructed a dual-layer pricing model for “one-ticket” intermodal transport, and Xin et al. [5] designed an intermodal service system based on the MaaS (Mobility as a Service) concept. However, these studies generally suffer from insufficient analysis of micro-level behavior, especially in failing to integrate user profiling technology to achieve precise demand layering. Notably, the application of user profiling in transportation is gradually emerging. For instance, Grison et al. [6] revealed the interactive effects of user attributes and situational factors on public transportation route choices using key event analysis methods; Moussa et al. [7] proposed a personalized passenger information system based on the ELECTRE multi-criteria decision method, combining dynamic weight optimization for public transport recommendation strategies. However, existing studies rarely focus on air-rail intermodal scenarios and often neglect the collaborative analysis of passengers' multidimensional attributes and travel characteristics. Based on this, this paper focuses on the construction of a comprehensive intermodal transport system between civil aviation and urban metro systems, using the K-means clustering algorithm [8, 9] for user segmentation. It proposes ticketing optimization strategies for different passenger groups, providing a theoretical basis for the “fine-grained” management and diversified services of the intermodal transport market.

2. Data collection

The purpose of this survey is to accurately grasp the travel demand characteristics of different passenger groups, thereby providing a solid data foundation for the subsequent ticketing optimization strategies. The survey content includes basic personal attributes and travel-related characteristics. Personal attributes cover gender, age, education level, occupation, and monthly income. Travel characteristics include travel purpose, frequency of use, travel expenditure, and reasons for choosing intermodal transport. The survey participants were limited to the Qingdao area to ensure that all respondents had real experience with air-rail intermodal transfers, either from high-speed rail to air travel or vice versa. A total of 1,060 valid questionnaires were collected.

The survey sample was gender-balanced, with the majority of respondents aged 19–30 (46.23%). Passengers with junior college or undergraduate education accounted for 58.43%, and office workers represented the largest occupational group (50.94%). More than 60% of the passengers were in the low- to middle-income brackets. In terms of travel characteristics, the main reasons for choosing intermodal transportation were time savings (50%) and cost savings (45.28%). Key factors influencing the choice of intermodal services were ticket price (79.25%), comfort (62.26%), and time (41.51%). The primary travel purposes were tourism (47.17%) and business/work (23.58%), with the combined share of these two groups exceeding 70%. Given their dominant proportion, the decision-making characteristics of tourists and business travelers have a decisive influence on the overall air-rail intermodal transport market.

To identify representative passenger groups, it was necessary to screen the variables involved in the survey and select appropriate variables for the K-means clustering process. The variables from the database of personal and travel attributes were tested in different combinations for clustering, and the clustering outcomes were evaluated. Ultimately, the variables used for K-means clustering were finalized as shown in Table 1:

Table 1. Selected Clustering Variables

3. Data processing and analysis

This study leverages the efficiency of the K-means algorithm in handling large-scale datasets. The optimal value of K is dynamically determined using the elbow method [10] and the silhouette coefficient method [11], allowing the model to adapt to different data distributions. Combined with feature engineering, the study conducts an in-depth analysis of passenger behavior, uncovering more valuable features to enhance clustering performance. This approach enables effective classification of air-rail intermodal passengers and the establishment of corresponding user labels, thereby supporting the delivery of more personalized services.

3.1. Clustering methodology for passenger profiling

3.1.1. Data preprocessing

Before conducting clustering analysis, the data underwent preprocessing. The dataset was checked for missing values. For variables with few missing values, imputation was done using the mean (for numerical variables) or mode (for categorical variables). Variables with excessive missing values were either removed or the related samples were excluded. Outliers were detected using the boxplot method [12], and the Winsorization technique [13] was applied to handle these outliers by capping extreme values with upper and lower bounds. Categorical variables were encoded into numerical form using dummy variable encoding to facilitate the clustering analysis.

3.1.2. Determining passenger cluster categories

The elbow method was used to identify the optimal number of clusters (K). The method involves calculating the total within-cluster sum of squares (SSE) for different values of K, and identifying the point where the rate of decline in SSE slows significantly — the so-called “elbow point.”

\( SSE=\sum _{i=1}^{k}\sum _{x∈{C_{i}}}||x-{μ_{i}}||_{2}^{2} \) (1)

Where \( k \) denotes the number of clusters; \( {C_{i}} \) represents the \( i-th \) cluster; \( x \) refers to the data points belonging to the \( i-th \) cluster; and \( {μ_{i}} \) is the centroid of the \( i-th \) cluster.

As K increases, SSE naturally decreases since additional centroids reduce the distance between points and their assigned centers. However, past a certain point, the marginal gain diminishes — this is identified as the “elbow,” where the trade-off between model complexity and clustering performance is balanced.

Using the selected clustering variables, the KMeans function from the Python scikit-learn machine learning toolkit was employed to construct the clustering model. The variation in mean squared error with increasing cluster numbers was visualized as a line graph (see Figure 1).

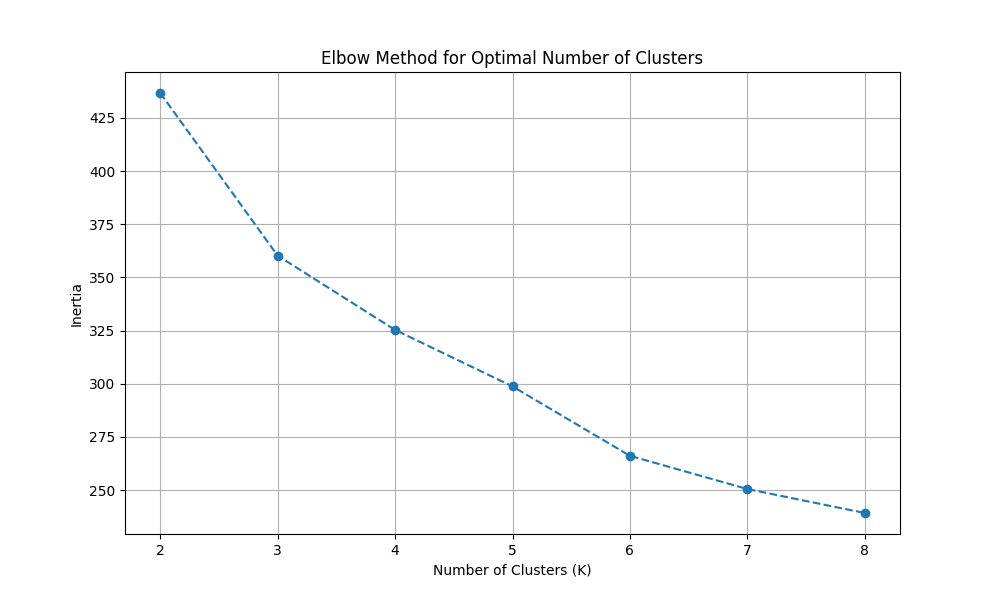
Figure 1. Relationship Between Number of Clusters and SSE

As shown, the SSE steadily decreases with an increase in the number of clusters, which aligns with expectations. Notably, the drop in SSE is steep between clusters 2 and 3, after which the decline slows. This supports the appropriateness of choosing K = 3.

3.1.3. Clustering results for air-rail intermodal passengers

After determining the number of clusters, SPSS software was used to iteratively cluster passenger data from Qingdao’s air-rail intermodal travel database, based on personal attributes and travel characteristics.

Cluster Center Update Formula: \( {C_{j}}=\frac{1}{{N_{j}}}\sum _{x∈{S_{j}}}x \) . Where \( {C_{j}} \) is the centroid of the j-th cluster, \( {N_{j}} \) is the number of data points in cluster j, and \( {S_{j}} \) denotes the set of points belonging to cluster j.

Distance from Point to Cluster Center Formula: \( ⅆ(x,{C_{j}})=\sqrt[]{\sum _{i=1}^{n}{({x_{i}}-{C_{j,i}})^{2}}} \) ,Where \( ⅆ(x,{C_{j}}) \) represents the distance from data point X to the centroid \( { C_{j}} \) of its corresponding cluster. Through multiple iterations, the algorithm updated cluster centers until convergence was achieved — that is, when centers remained constant or changed minimally. This ensured algorithmic stability and a reliable clustering outcome. The details are shown in Table 2 and Table 3:

Table 2. Final Cluster Centers

Table 3. Sample Distribution by Cluster

Based on the K-means clustering results, the passengers were classified into three categories: Cluster 1, Cluster 2, and Cluster 3. Their proportions in the total sample were 37%, 35%, and 28%, respectively. These clusters were then labeled as follows: Cluster 1: Business Travelers; Cluster 2: Leisure Travelers; Cluster 3: Budget Travelers

​To visually validate the clustering results, a two-dimensional scatter plot was generated using the Seaborn library in Python, showing the distribution of passenger groups based on two core dimensions — monthly income and travel expenditure (see Figure 2).

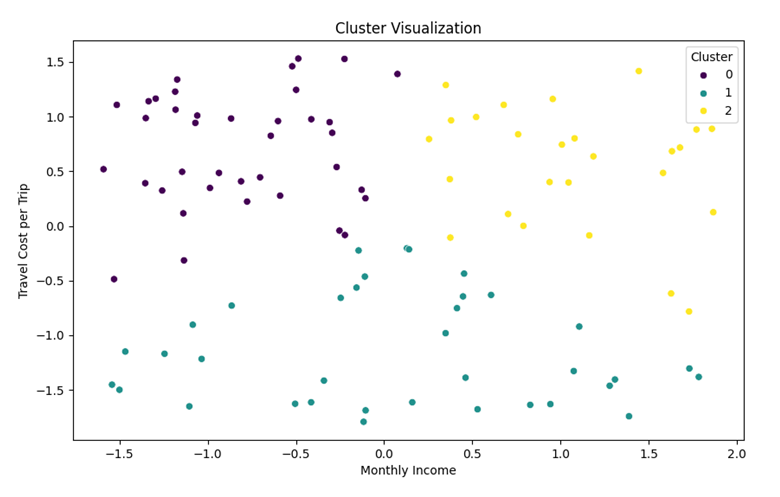
Figure 2. Clustering Results Visualization

3.2. Evaluation of passenger profiling for Qingdao’s air-rail intermodal transport

The silhouette coefficient method was used to evaluate the clustering quality and adjust the model if necessary.

Silhouette Coefficient Formula: \( s(i)=\frac{b(i)-a(i)}{max\lbrace a(i),b(i)\rbrace } \) (2)

Where \( a(i) \) : For each passenger data point \( i \) , calculate the average distance between that point and all other points within the same cluster;

\( b(i) \) : For each passenger data point \( i \) , calculate the average distance between that point and all points in the nearest other cluster. For example, for Category 1 (business travelers), compute the average distance between each business traveler data point and all points in Category 2 (leisure travelers) or Category 3 (economy travelers), and take the minimum of these averages as \( b(i) \) .

By averaging the silhouette coefficients of all passenger data points, the overall silhouette score is obtained. The average silhouette coefficient across all data points was 0.58, indicating that the clustering result is reasonably good, and the passenger segmentation is appropriately defined.

4. Optimization plan for air-rail intermodal ticketing

To address the issues of supply-demand mismatch and a single pricing mechanism in Qingdao Jiaodong Airport’s air-rail intermodal services, this section proposes a differentiated ticketing strategy system based on the previously constructed passenger clustering model—Business Travelers, Leisure Travelers, and Budget Travelers.

4.1. Business travelers

Accounting for 37% of the total passenger population, business travelers are primarily driven by the value of time and exhibit significantly higher annual travel frequencies compared to other groups, making them highly loyal customers. Therefore, optimizing ticketing services for this time-sensitive group is crucial. Recommendations include: Priority security screening lanes; Dedicated shuttle services directly connecting passengers to the security checkpoint within the airport; Post-departure transport arrangements; Direct luggage delivery to hotels. These value-added services aim to minimize travel time. Furthermore, a suite of VIP and priority services should be integrated to fully meet this group’s expectations for premium service quality.

4.2. Leisure travelers

Comprising 35% of the sample, leisure travelers prioritize comfort and present high potential for growth. Their travel patterns are concentrated around holiday peak periods, which makes enhancing travel experience value especially important. Suggested optimization strategies include: Improving on-time performance of flights; Offering compensation and care measures for delays to enhance customer satisfaction; Launching “Cultural and Tourism Express” product lines; Implementing flexible refund and change policies; Developing seasonal floating pricing systems. These initiatives aim to strengthen customer engagement and foster brand loyalty.

4.3. Budget travelers

Making up 28% of the passenger population, budget travelers are highly price-sensitive, focusing on cost-effectiveness and value for money. They are particularly concerned about fees for ticket changes and cancellations, which significantly influence their travel decisions. To attract this segment, airlines can implement various preferential measures: Launch “intermodal travel packages” combining second-class rail seats with economy-class flight tickets; Offer early-bird tiered discounts; Designate off-peak fare zones with special rates. Additionally, supporting services such as dedicated booking channels for students and senior citizens and real-time price alert features can improve affordability and accessibility.

By applying real-time clustering analysis, the ticketing system can optimize resource allocation, improve order processing efficiency during peak times, and increase revenue from intermodal products. Furthermore, integrating data interfaces among air, rail, and road transport operators, along with establishing cross-transport revenue-sharing mechanisms, can significantly reduce complaint rates, and enhance the overall quality of intermodal services.

5. Conclusion

Despite limitations in sample scope, which did not cover a broader demographic range, this study employed a K-means clustering algorithm based on user profiling to conduct in-depth market segmentation of passengers using Qingdao Jiaodong Airport’s air-rail intermodal services. The research identified the distinct demand characteristics and behavioral differences among Business, Leisure, and Budget passenger groups, providing a solid theoretical basis for ticketing optimization. The proposed personalized ticketing strategies aim to address issues such as supply-demand mismatches and uniform pricing mechanisms, while also enhancing passenger experience and improving the competitiveness of intermodal services. Future research should consider expanding the survey scope, enriching the data sample, and incorporating more influencing factors and variables to further explore passenger needs, thus offering a more comprehensive and in-depth framework for optimizing intermodal ticketing systems.