1. Introduction
With the rapid development of wireless communication, radar stealth technology, and various high-frequency electronic devices, issues related to Electromagnetic Interference (EMI) and Electromagnetic Radiation (EMR) have become increasingly severe. In order to mitigate electromagnetic wave interference, Microwave Absorbing Materials (MAMs) have emerged as a critical solution. Radar Absorbing Materials (RAMs) work by absorbing the energy of electromagnetic waves, thereby reducing their reflection and transmission, and ultimately achieving effective electromagnetic shielding. The performance of RAMs is particularly vital in the fields of stealth technology and Electromagnetic Compatibility (EMC).
According to their electromagnetic wave attenuation mechanisms, absorbing materials can be primarily categorized into magnetic loss-type, dielectric loss-type, and resonance loss-type. Materials fabricated using magnetic absorbers often suffer from drawbacks such as heavy weight, poor corrosion resistance, and weak mechanical properties. In contrast, dielectric loss-type absorbing materials can overcome these shortcomings [1, 2]. Dielectric loss absorbers include activated carbon fibers, porous carbon fibers, nanocarbon fibers, carbon nanotubes, silicon carbide fibers, fibers with special-shaped cross-sections, polycrystalline iron fibers, magnetic fibers, ferrite fibers, and various surface-modified or composite-modified fibers. A great deal of research has focused on improving the attenuation strength, bandwidth, and thickness optimization of such materials [3, 4]. These studies have consistently demonstrated the superiority of dielectric loss-type materials in achieving lightweight, broadband, and corrosion-resistant absorption performance. Most studies on these absorbers focus on optimizing material selection and layer thickness based on a fixed number of impedance gradient layers to enhance reflection loss performance. However, few efforts have been made to systematically explore the relationship between electromagnetic parameters and absorption performance.
The absorption performance of a material is primarily determined by its electromagnetic parameters, such as permittivity, permeability, and loss factors. These parameters define the material's ability to absorb electromagnetic waves across different frequency ranges. Determining the value ranges of key parameters required for optimal performance is of both theoretical and practical significance in the design and development of absorbing materials. A key challenge in this process is how to identify the optimal combination of parameters within a high-dimensional parameter space to maximize performance. Traditional optimization methods, such as gradient descent, simulated annealing, and genetic algorithms, often require extensive computation and experimental validation. They are also prone to local optima and are inefficient in exploring vast solution spaces [5].
In recent years, with the rapid advancement of artificial intelligence, neural network algorithms have proven to be powerful nonlinear modeling tools and have shown remarkable effectiveness in solving complex optimization problems. Neural networks can learn from large datasets, automatically extract underlying patterns, and identify global optimal solutions in complex, high-dimensional parameter spaces [6, 7]. Their application in optimizing the electromagnetic parameters of dielectric loss-type radar absorbing coatings has shown high accuracy and efficiency. Therefore, this study focuses on the application of neural network algorithms in optimizing the electromagnetic parameters of dielectric loss-type radar absorbing coatings, and analyzes their advantages and limitations.
2. Overview of neural network algorithms
Neural Networks (NNs) are algorithms that simulate the information processing mechanisms of biological neural systems. By interconnecting a large number of artificial neurons into a multilayer structure, neural networks can automatically extract features from input data and perform nonlinear mappings. With their powerful learning and pattern recognition capabilities, neural networks have been widely applied to tasks such as regression, classification, and optimization.
A typical neural network consists of an input layer, one or more hidden layers, and an output layer, as illustrated in Figure 1. During the training process, the network adjusts its weights and biases using the Backpropagation (BP) algorithm to minimize prediction error. Common neural network models include Feedforward Neural Networks (FNN), Convolutional Neural Networks (CNN), and Long Short-term Memory Networks (LSTM).
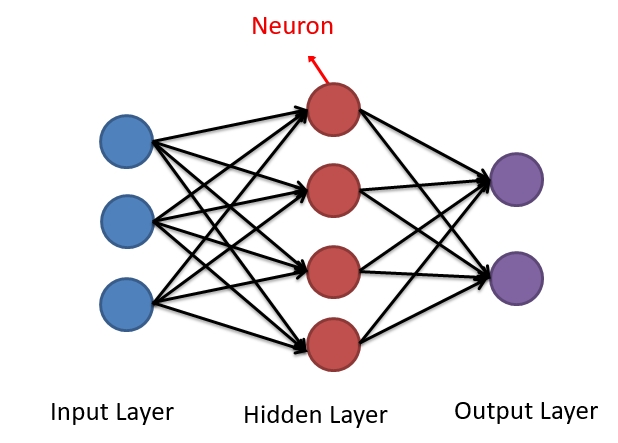
In the optimization of electromagnetic parameters for dielectric loss-type microwave absorbing materials, neural network algorithms are primarily used to establish the mapping relationship between a material’s electromagnetic parameters and its absorption performance. By training neural network models, it is possible to learn the underlying influence patterns of electromagnetic parameters on absorption performance from large volumes of experimental or simulation data. Based on predefined optimization goals, the neural network can then automatically adjust the electromagnetic parameters to achieve optimal absorption performance.
3. Application of neural networks in the optimization of electromagnetic parameters for dielectric loss absorbing materials
3.1. Establishing the mapping between electromagnetic parameters and absorption performance
The optimization design of dielectric loss absorbing materials involves multiple electromagnetic parameters, including permittivity (
When applying neural network algorithms to optimize the electromagnetic parameters of dielectric loss absorbing materials, the primary task is to establish a mapping relationship between these parameters and the materials’ absorption performance. The simulated data samples used in this study include absorption characteristics (e.g., absorption peak, bandwidth, reflection loss) under various electromagnetic parameter combinations.
The simulated samples are obtained using the following formulas:
and
Where: RL is the reflection loss, Zin is the input impedance, j is the imaginary unit, c is the speed of light in free space, f is the microwave frequency, and d is the sample thickness. These formulas establish a nonlinear mapping between the reflection loss and the real and imaginary parts of the permittivity in dielectric loss absorbing materials. A dataset of electromagnetic parameters and corresponding reflection loss values is generated and used as input-output pairs for training the neural network. Through this training process, the model learns the nonlinear relationship between the parameters and the absorption performance. The results are visualized in two-dimensional plots of reflection loss vs. real and imaginary parts of permittivity. A total of 2,000 training samples were used, and the modeling process was implemented in MATLAB. The full training procedure is shown in Figure 2.
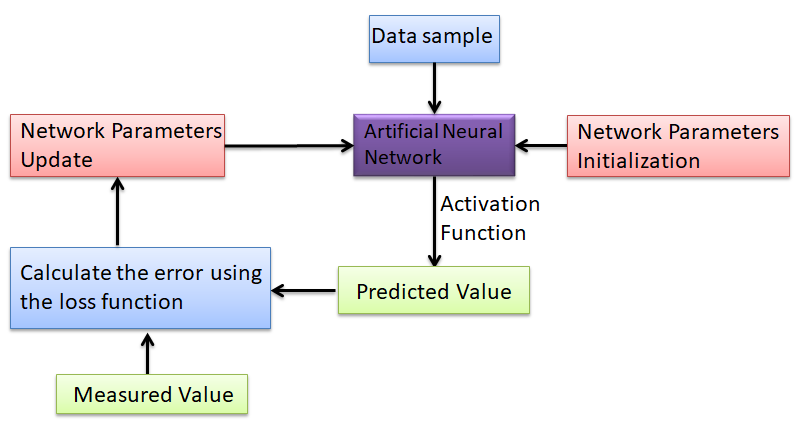
3.2. Results and discussion
3.2.1. Electromagnetic parameter and absorption performance generation based on neural networks
After establishing the mapping between electromagnetic parameters and absorption performance, the neural network can be used to optimize the selection of these parameters. Based on the input of initial electromagnetic parameters, the neural network predicts the corresponding absorption performance and adjusts the weights through backpropagation to eventually identify an optimal set of parameters. Initially, two-dimensional plots were generated for the relationship between electromagnetic parameters and reflection loss at a frequency of 10 GHz (wavelength = 30 mm) for materials of various thicknesses. These are shown in Figure 3.
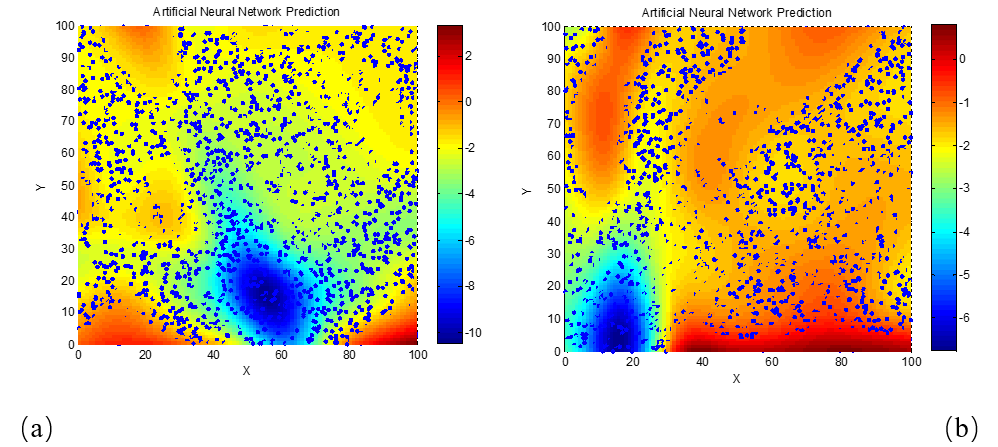
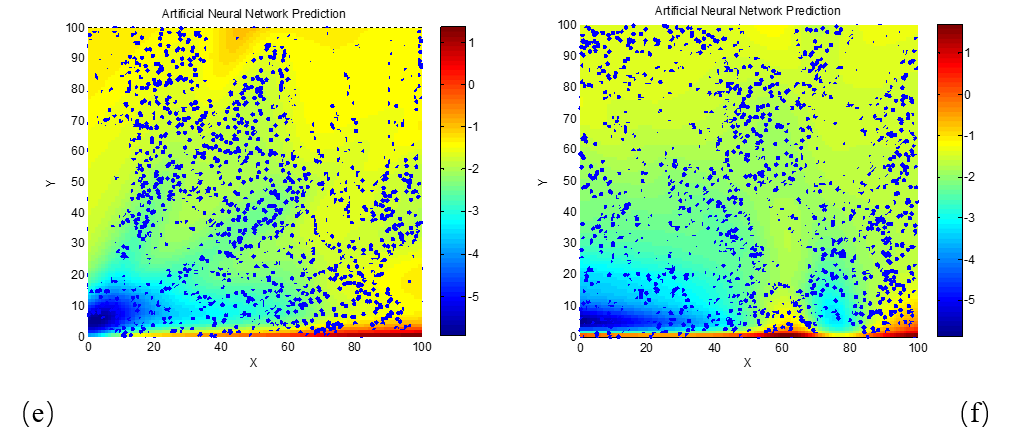
(a) d = 1 mm; (b) d = 2 mm; (c) d = 3 mm; (d) d = 4 mm; (e) d = 5 mm; (f) d = 6 mm; (g) d = 7 mm; (h) d = 8 mm; (i) d = 9 mm; (j) d = 10 mm
As shown in Figure 3, the horizontal axis represents the real part of permittivity, the vertical axis represents the imaginary part, and the color gradient from red to blue indicates decreasing reflection loss. The blue regions indicate areas with better absorption performance. From the relationship between reflection loss and permittivity at 10 GHz, we observe that as the material thickness increases, both the real and imaginary parts of the permittivity must be constrained to smaller values in order to minimize reflection loss. At smaller thicknesses, multiple parameter regions with low reflection loss emerge, and these regions tend to be wider, with the real part often significantly larger than the imaginary part. Additionally, combining the results of Figure 3 and formula (2), it can be seen that reflection loss is more sensitive to variations in electromagnetic parameters than to frequency or thickness. The influence of thickness is also visible in the patterns of Figure 3. To further examine the sensitivity of reflection loss to frequency changes, we analyze the matching characteristics between electromagnetic parameters and thickness at a frequency of 8 GHz.
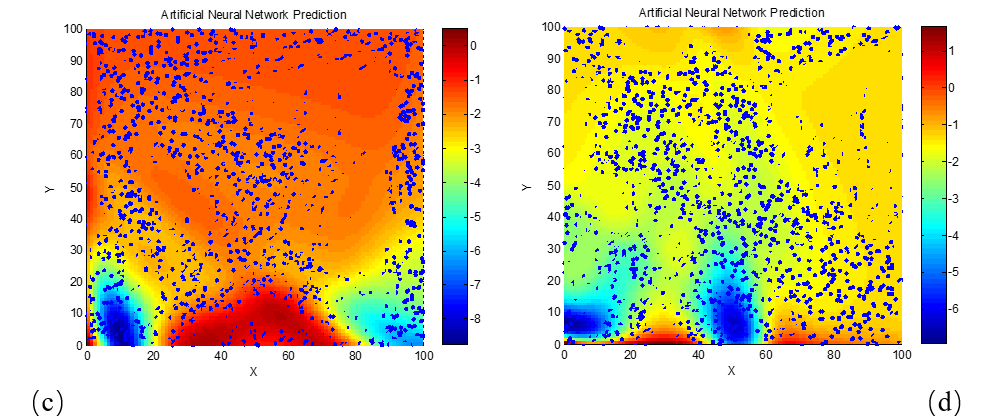
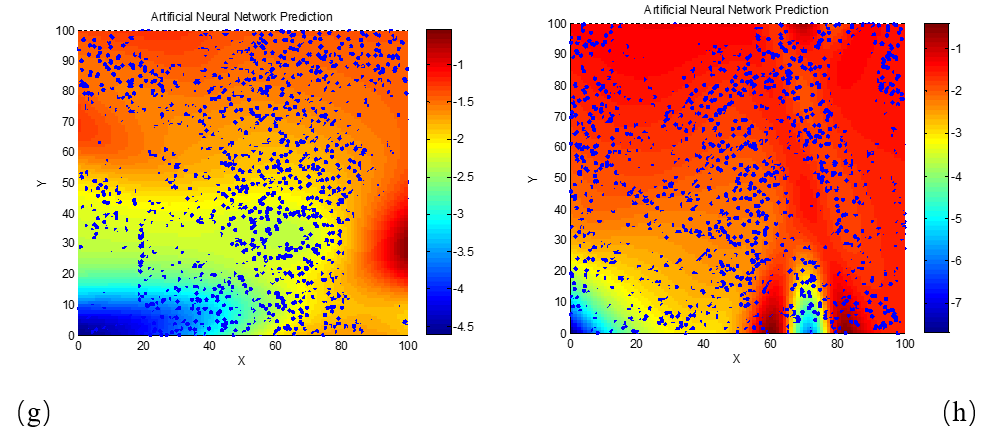
(a) d = 1 mm; (b) d = 2 mm; (c) d = 3 mm; (d) d = 4 mm; (e) d = 5 mm; (f) d = 6 mm; (g) d = 7 mm; (h) d = 8 mm; (i) d = 9 mm; (j) d = 10 mm
From the data and plots in Figure 4, it is evident that the variation trends in the optimal electromagnetic parameter regions for achieving excellent absorption performance at 8 GHz are essentially the same as those observed at 10 GHz. This suggests that the reflection loss’s sensitivity to the matching of electromagnetic parameters is only minimally affected by changes in frequency.
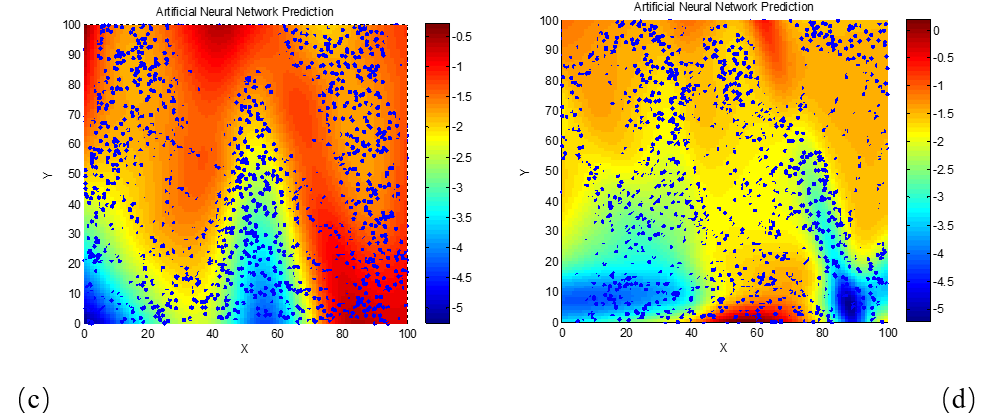
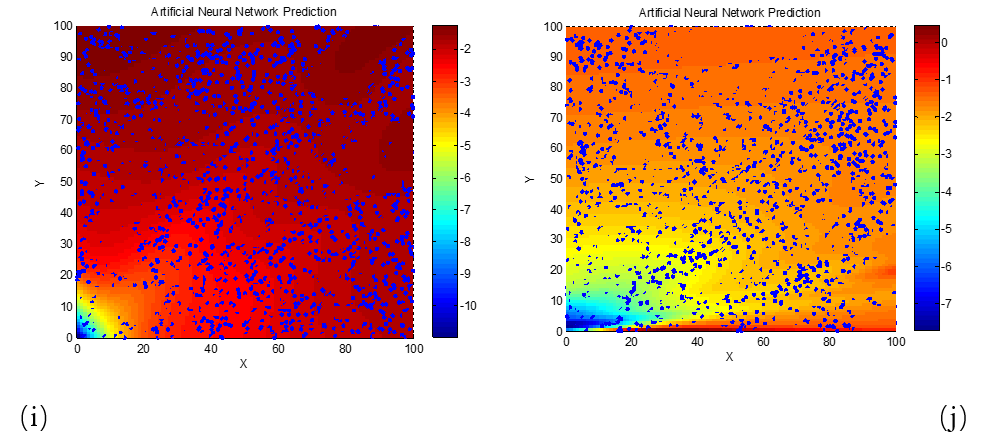
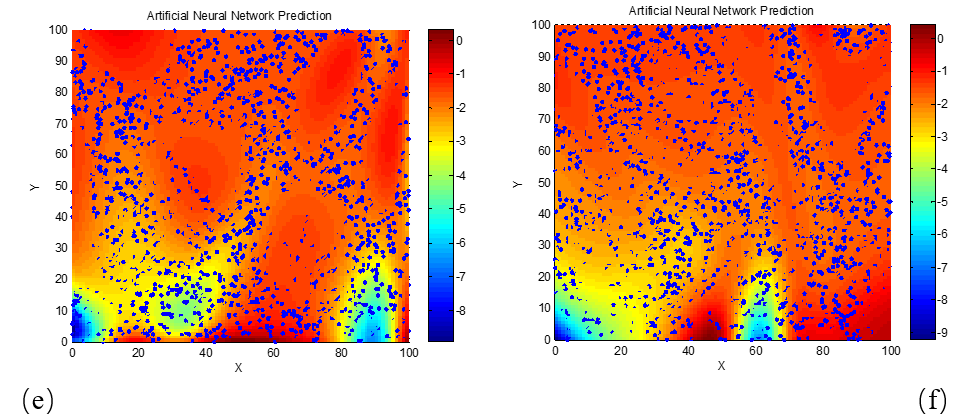
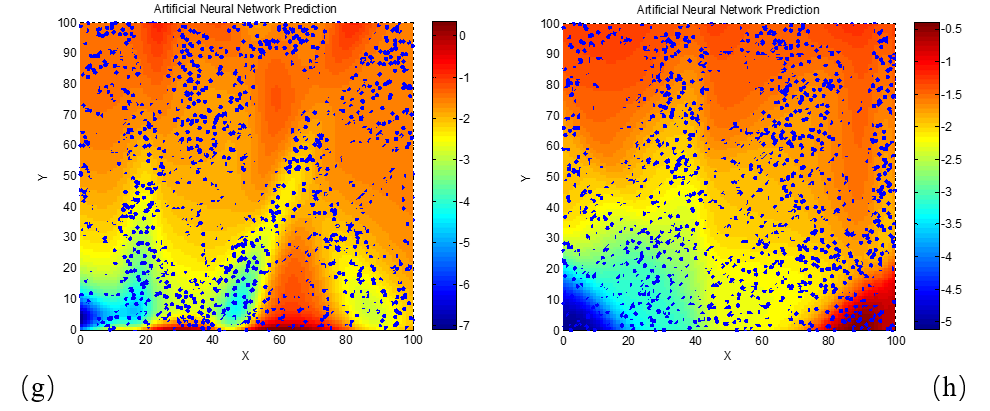
To further examine how the reflection loss of dielectric loss absorbing materials varies with frequency (or wavelength), and to determine the corresponding required electromagnetic parameter characteristics, the relationships between reflection loss and the real and imaginary parts of permittivity were also studied at 3 GHz and 18 GHz. These relationships were similarly modeled and visualized using neural network algorithms, as shown in Figure 5.
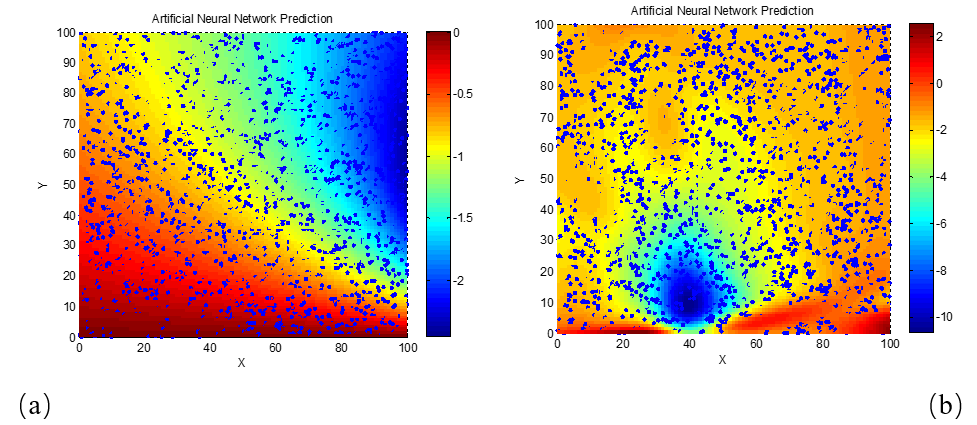
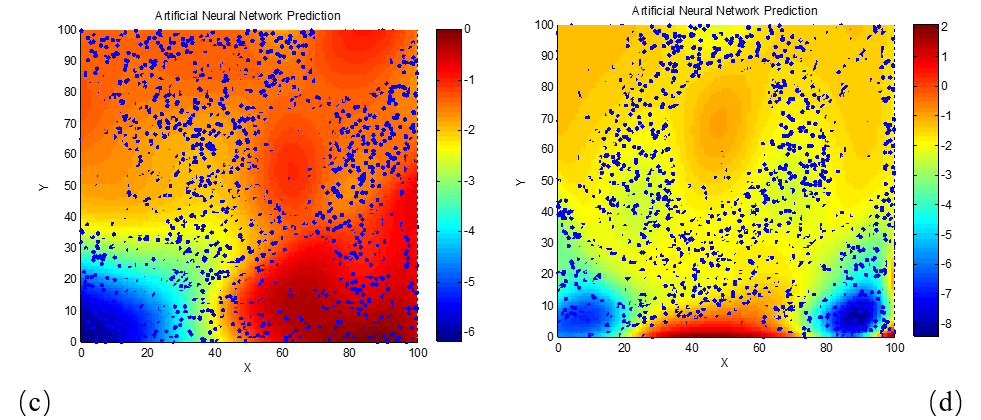
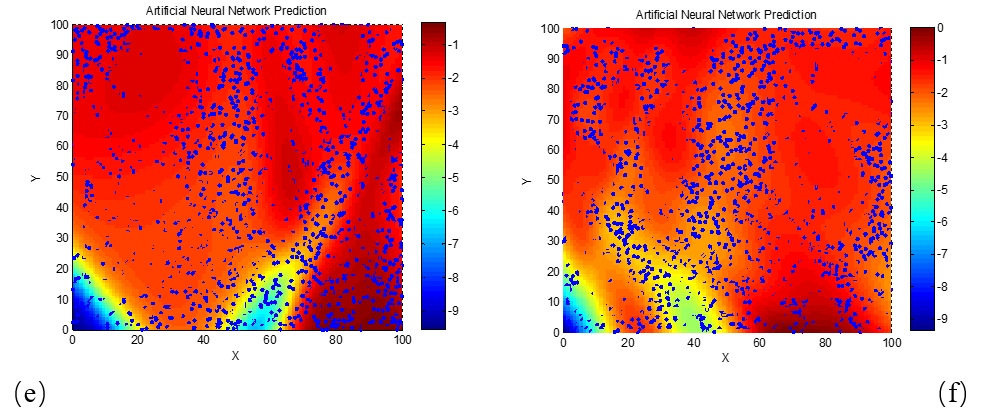
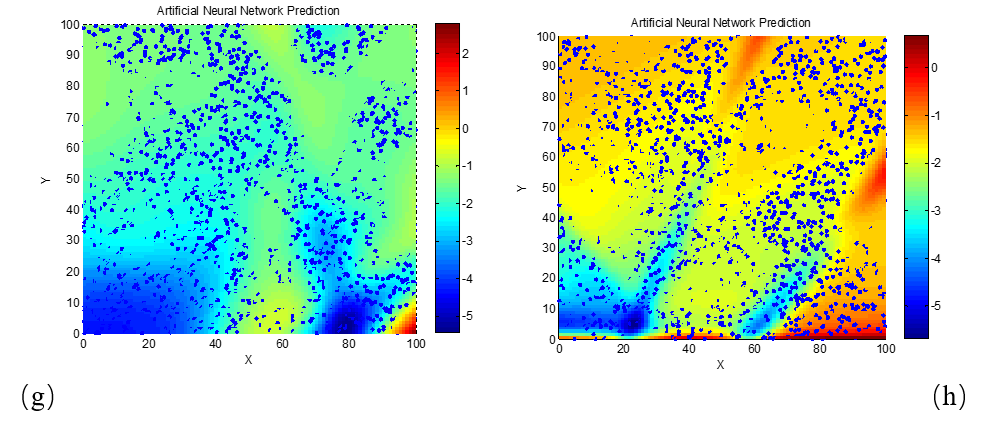
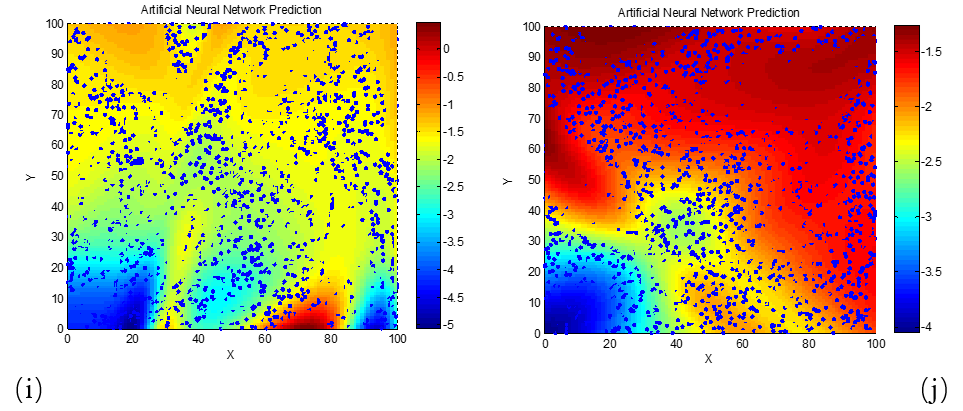
(a) d = 2 mm; (b) d = 4 mm; (c) d = 6 mm; (d) d = 8 mm; (e) d = 10 mm; (f) d = 12 mm; (g) d = 14 mm; (h) d = 16 mm; (i) d = 18 mm; (j) d = 20 mm
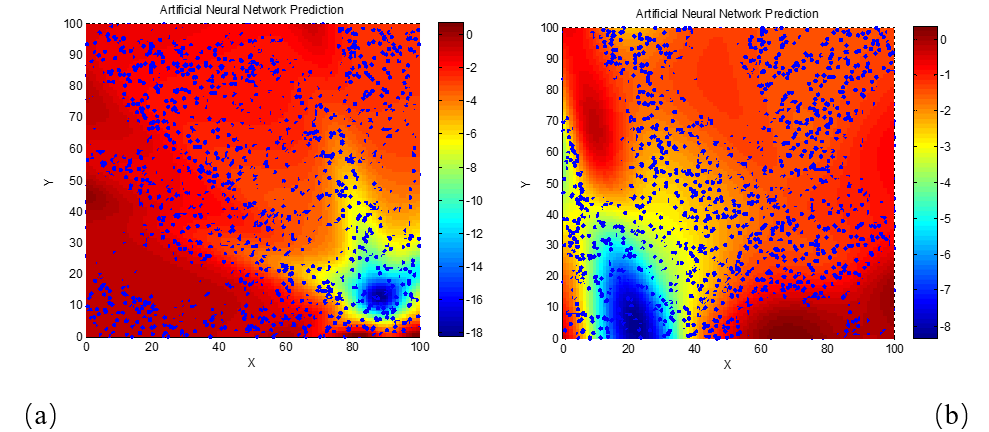
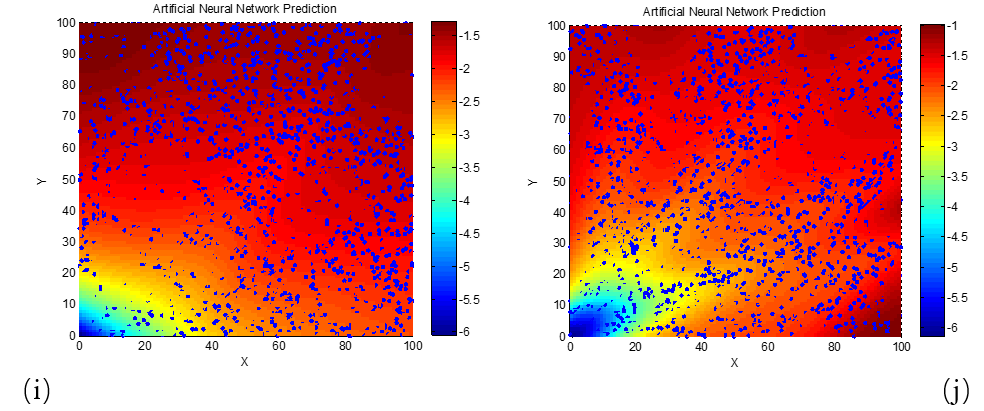
As clearly seen in Figure 5, for the 3 GHz frequency, the phenomenon of high-performance absorption requiring lower real and imaginary permittivity values becomes apparent only when the material thickness reaches 20 mm. This is likely due to the longer wavelength of 3 GHz electromagnetic waves compared to those in the X-band (e.g., 8 GHz and 10 GHz). The longer wavelength increases the matching thickness needed for destructive interference and energy dissipation, thereby explaining this observation. To verify this explanation, we next examine a higher frequency scenario with a shorter wavelength. Neural network algorithms were used to generate the reflection loss–permittivity relationship maps at 18 GHz, as shown in Figure 6.
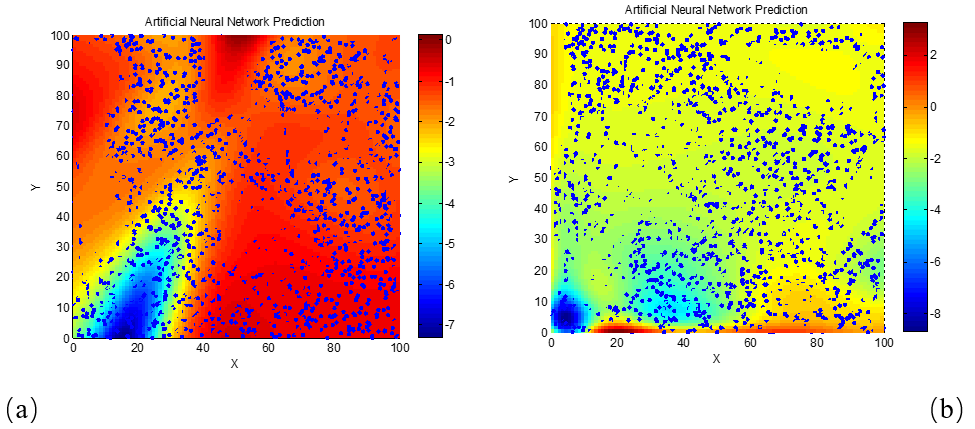
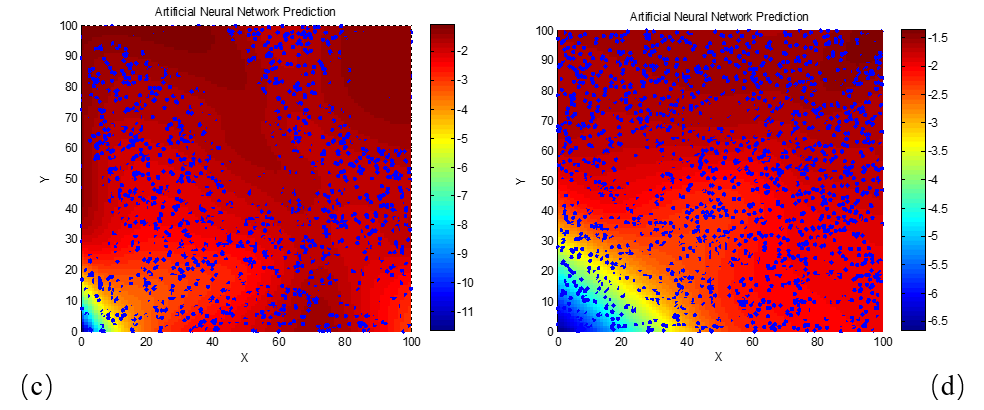
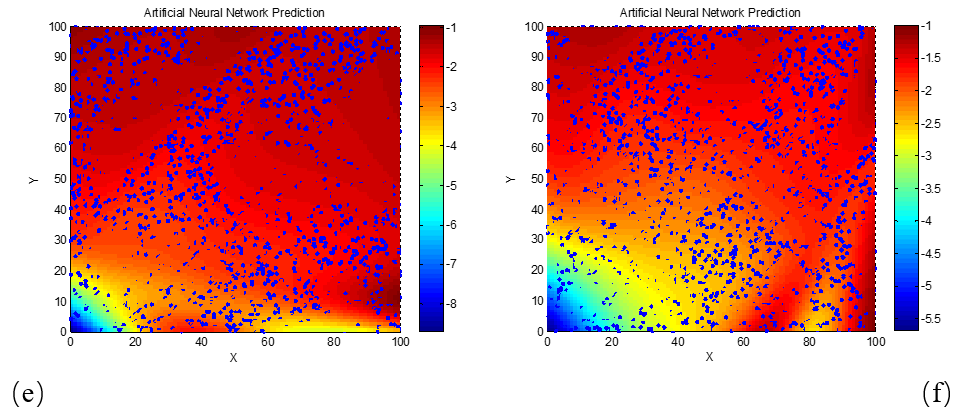
(a) d = 1 mm; (b) d = 2 mm; (c) d = 3 mm; (d) d = 4 mm; (e) d = 5 mm; (f) d = 6 mm
From the results in Figure 6, it is evident that as the frequency increases to 18 GHz and the electromagnetic wavelength decreases, the optimal real and imaginary parts of the permittivity for achieving maximum absorption performance become concentrated in smaller value regions even at relatively small material thicknesses. When the material thickness reaches just 6 mm, the permittivity values corresponding to a reflection loss of −5 dB are already less than 10 for both the real and imaginary parts. These findings confirm the earlier explanation regarding the effect of wavelength on matching thickness and optimal parameter concentration.
3.2.2. Experimental validation
Three types of dielectric loss microwave-absorbing materials were fabricated, and their electromagnetic parameters in the frequency range of 2–18 GHz were measured using the coaxial method. The real and imaginary parts of permittivity at 3 GHz, 8 GHz, 10 GHz, and 18 GHz are shown in Table 1.
|
Frequency (GHz) Material & Parameter |
3 |
8 |
10 |
18 |
|
|
Material 1 |
Real part of |
4.61 |
4.20 |
4.02 |
3.87 |
|
Imaginary part of |
0.84 |
0.77 |
0.78 |
0.78 |
|
|
Material 2 |
Real part of |
6.74 |
5.84 |
5.51 |
5.01 |
|
Imaginary part of |
2.55 |
1.81 |
1.73 |
1.51 |
|
|
Material 3 |
Real part of |
30.9 |
16.7 |
14.8 |
10.3 |
|
Imaginary part of |
39.5 |
20.8 |
18.0 |
14.0 |
|
As shown in Table 1, both the real and imaginary parts of permittivity increase progressively from Material 1 to Material 3. For comparative analysis, thicknesses of 2 mm, 4 mm, and 6 mm were selected. Using the measured electromagnetic parameters, the corresponding reflection loss curves for the three materials at each thickness were calculated, as illustrated in Figure 7.
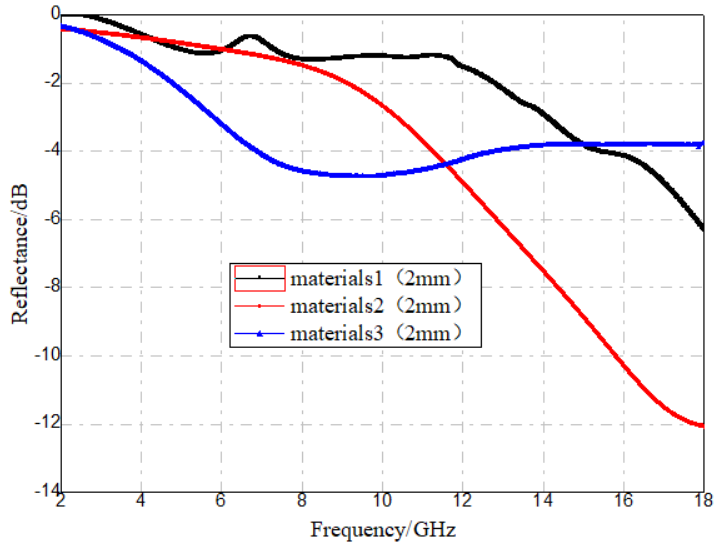
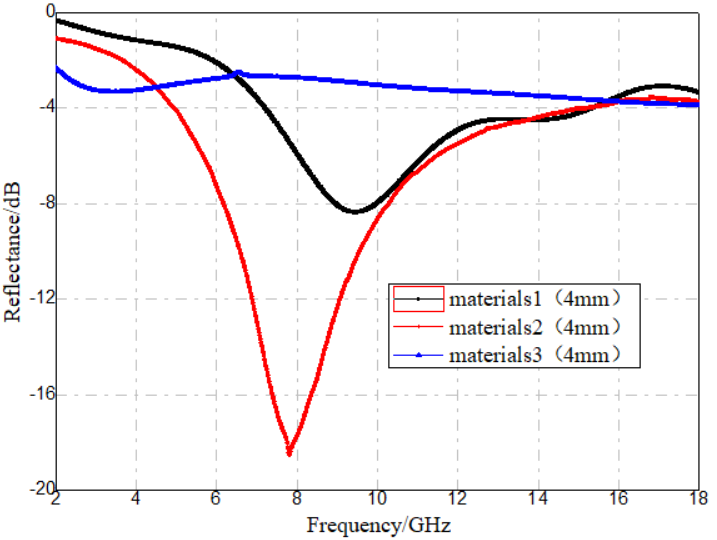
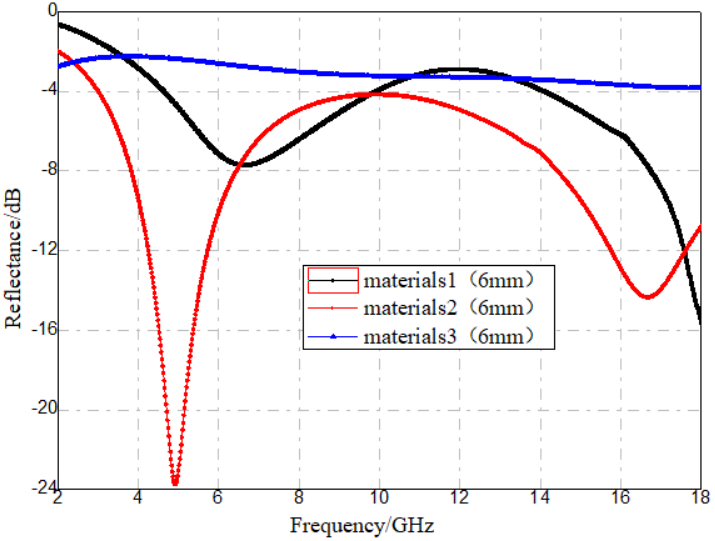
Figure 7. Reflection loss of three dielectric loss absorbing materials (a) Thickness = 2 mm (b) Thickness = 4 mm (c) Thickness = 6 mm
By comparing the reflection loss curves in Figure 7 with the neural network–predicted reflection loss–permittivity mappings, it is evident that the predicted values are generally consistent with the calculated values based on experimental measurements. This confirms that neural network algorithms possess good practical applicability for predicting the absorption performance of dielectric loss materials.
4. Conclusion and outlook
In this study, neural network algorithms were used to predict the reflection loss distribution of dielectric loss microwave-absorbing materials when both the real and imaginary parts of permittivity were treated as variables. The variation patterns in reflection loss as functions of frequency and material thickness were also analyzed. The results indicate that the reflection loss distribution of dielectric loss materials is relatively insensitive to disturbances in frequency and thickness. However, the optimal electromagnetic parameters and matching thicknesses for minimizing reflection loss vary with frequency. As the thickness increases, the required real and imaginary parts of permittivity must gradually be constrained to lower values in order to minimize reflection loss. At lower frequencies (i.e., longer wavelengths), greater thicknesses are required to achieve minimum reflection loss. Conversely, as frequency increases, the optimal real and imaginary parts of permittivity for achieving strong absorption tend to concentrate in lower value ranges even at smaller thicknesses. Although the application of neural network algorithms in absorbing materials is still evolving, future advancements are expected in the following areas: (1) Application of Deep Learning: As deep learning technologies progress, more sophisticated neural network structures—such as Convolutional Neural Networks (CNNs) and Generative Adversarial Networks (GANs)—can be leveraged to further improve optimization accuracy and efficiency. (2) Multi-Objective Optimization: In practical applications, dielectric loss absorbing materials often require optimization of multiple objectives simultaneously, such as bandwidth and reflection loss. Combining neural networks with multi-objective optimization algorithms can enhance overall effectiveness. (3) Integration of Reinforcement Learning: With reinforcement learning techniques, neural networks can dynamically adapt and optimize in real-time, improving their adaptability and performance in complex environments.
References
[1]. Zhou, Z., Liu, Y., Chen, X., Wang, Z., & Zhao, Y. (2024). Study on properties of glass-fiber-fabric-reinforced microwave-absorbing composites.Materials, 17(7), 1453. https: //doi.org/10.3390/ma17071453
[2]. Zhou, M., Chen, Y., He, Y., & Yang, C. (2024). Ultra-thin and broadband P-band metamaterial absorber based on carbonyl iron powder composites.Materials,17(5), 1157. https: //doi.org/10.3390/ma17051157
[3]. Xu, J., Li, W., & Huang, C. (2010). Optimization design of dielectric-gradient carbon nanotube/epoxy microwave-absorbing materials based on genetic algorithm.Functional Materials, 41(S1), 155-158.
[4]. Choi, J., & Jung, H.-T. (2015). A new triple-layered composite for high-performance broadband microwave absorption.Composite Structures, 122, 166–171. https: //doi.org/10.1016/j.compstruct.2014.11.020
[5]. Cai, C. (2023).Research on optimization of microwave absorbing materials based on machine learning(Doctoral dissertation, University of Electronic Science and Technology of China).
[6]. Xie, Y., Zhao, X., & Liu, Z. (2023). A simple approach for wave absorbing control of plunger wavemakers using machine learning: Numerical study.Coastal Engineering, 179, Article 104253. https: //doi.org/10.1016/j.coastaleng.2022.104253
[7]. Li, L., Yuan, Z., & Gao, Y. (2018). Maximization of energy absorption for a wave energy converter using the deep machine learning.Energy, 165(Part A), 340–349. https: //doi.org/10.1016/j.energy.2018.09.093
Cite this article
Cheng,H.;Wang,H.;Wang,Z.;Wang,Z. (2025). Application of neural network algorithms in the design of electromagnetic parameters for dielectric loss microwave absorbing materials. Advances in Engineering Innovation,16(6),74-83.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Journal:Advances in Engineering Innovation
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Zhou, Z., Liu, Y., Chen, X., Wang, Z., & Zhao, Y. (2024). Study on properties of glass-fiber-fabric-reinforced microwave-absorbing composites.Materials, 17(7), 1453. https: //doi.org/10.3390/ma17071453
[2]. Zhou, M., Chen, Y., He, Y., & Yang, C. (2024). Ultra-thin and broadband P-band metamaterial absorber based on carbonyl iron powder composites.Materials,17(5), 1157. https: //doi.org/10.3390/ma17051157
[3]. Xu, J., Li, W., & Huang, C. (2010). Optimization design of dielectric-gradient carbon nanotube/epoxy microwave-absorbing materials based on genetic algorithm.Functional Materials, 41(S1), 155-158.
[4]. Choi, J., & Jung, H.-T. (2015). A new triple-layered composite for high-performance broadband microwave absorption.Composite Structures, 122, 166–171. https: //doi.org/10.1016/j.compstruct.2014.11.020
[5]. Cai, C. (2023).Research on optimization of microwave absorbing materials based on machine learning(Doctoral dissertation, University of Electronic Science and Technology of China).
[6]. Xie, Y., Zhao, X., & Liu, Z. (2023). A simple approach for wave absorbing control of plunger wavemakers using machine learning: Numerical study.Coastal Engineering, 179, Article 104253. https: //doi.org/10.1016/j.coastaleng.2022.104253
[7]. Li, L., Yuan, Z., & Gao, Y. (2018). Maximization of energy absorption for a wave energy converter using the deep machine learning.Energy, 165(Part A), 340–349. https: //doi.org/10.1016/j.energy.2018.09.093









