1. Background of the Circle Division Problem

The problem of dividing the circumference of a circle, also known as the circle division problem, is a classic issue in ancient mathematics, involving the technology and methods of dividing the circumference of a circle into several equal parts. This problem holds an important position in the history of mathematics. It not only shows the development of geometry but also has a profound impact on the formation of later algebra, modern mathematics, and even modern abstract mathematics.

The history of the problem of dividing the circumference of a circle can be traced back to ancient Greece. Mathematicians at that time were particularly interested in geometric shapes, especially the circle, which was considered a perfect shape. The initial work of dividing the circumference of a circle was mainly completed through geometric drawing, such as using a straightedge and compass. Ancient Greek mathematicians believed that all geometric problems should be solvable with these simple tools.

One of the most famous methods of dividing the circumference of a circle was proposed by the ancient Greek mathematician Hippasus, who attempted to approximate the division of the circle by increasing the number of sides of a regular polygon. For example, one could first draw an inscribed equilateral triangle, then a square, a pentagon, a hexagon, gradually increasing the number of sides, and theoretically, one can infinitely approach the circumference of the circle, but in practice, only a finite precision of approximation can be achieved.

However, with the deepening of mathematical research, it was found that not all problems of dividing the circumference of a circle can be solved with just a straightedge and compass. A famous example is the trisection of an angle, which is to divide any given angle into three equal angles. Ancient Greek mathematicians spent a lot of effort studying this problem but never found a solution using only a straightedge and compass. It was not until the 19th century, with the help of algebra and more advanced mathematical tools, that it was finally proven that this problem cannot be solved using traditional straightedge and compass.

In addition, with the development of algebra, the problem of dividing the circumference of a circle has gradually been transformed into solving radical equations. For example, the 17th-century French mathematician Pierre de Fermat proposed that to construct a regular polygon with a straightedge and compass, the number of sides must be a Fermat prime or a product of several different Fermat primes multiplied by a power of 2. Gauss, at the age of 18, discovered the conditions for constructing the corresponding regular polygons with a straightedge and compass, thus solving the problem of the constructibility of regular polygons since ancient Greece.

In modern mathematics, the problem of dividing the circumference of a circle has turned to more abstract fields, such as abstract algebra and Galois theory, which provide a broader framework for studying the solvability of radicals and more types of geometric construction problems. Modern technology, such as computer graphics and numerical methods, also enables us to perform more precise and complex divisions of the circumference of a circle, no longer limited by the physical limitations of traditional tools.

In summary, the problem of dividing the circumference of a circle is an extremely important milestone in the history of mathematical development. It has not only promoted the development of geometry but also driven the innovation of algebra and mathematical methodology. The mathematical techniques and theories involved in this problem have always been the focus of mathematicians' research and exploration from ancient times to the present, reflecting the continuous deepening and expansion of human understanding and application ability in mathematics.

2. Methods for Precise Circle Division Construction

2.1. Trisection and Sextant Division of a Circle

2.1.1. Trisection

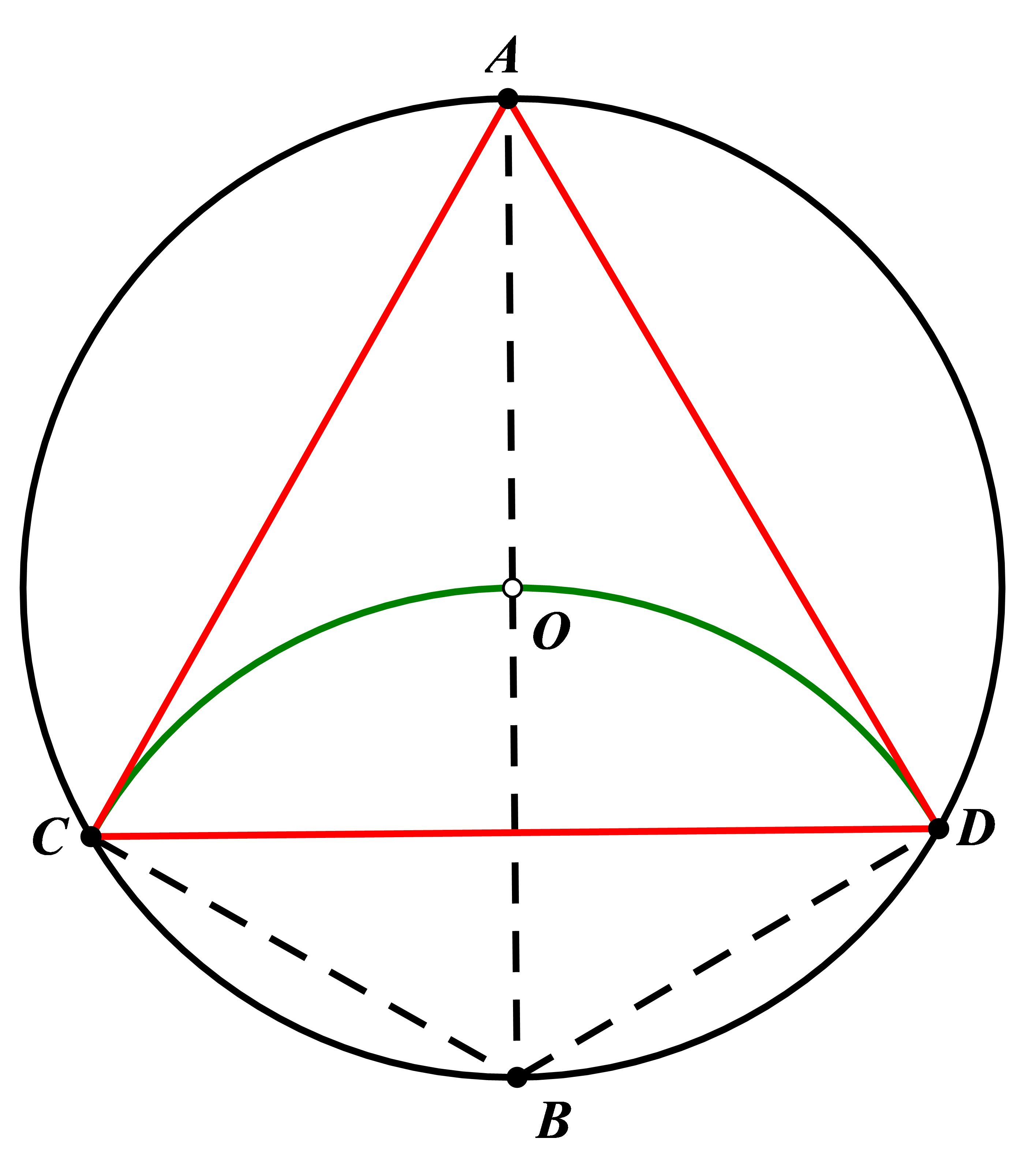
Figure 1. Method

Passing through the center of the circle O, draw any diameter AB. Take A as the center and AO as the radius to draw an arc intersecting the circumference of the circle at points C and D. Connect AC, CD, and DA. Triangle ACD is then an inscribed equilateral triangle within the circle.

Principle: Connect OD and OC. It is evident that triangles OBD and OCB are equilateral, hence ∠BOD = ∠BOC = 60°. Therefore, it is clear that triangle ACD is an equilateral triangle.

2.1.2. Sextant Division

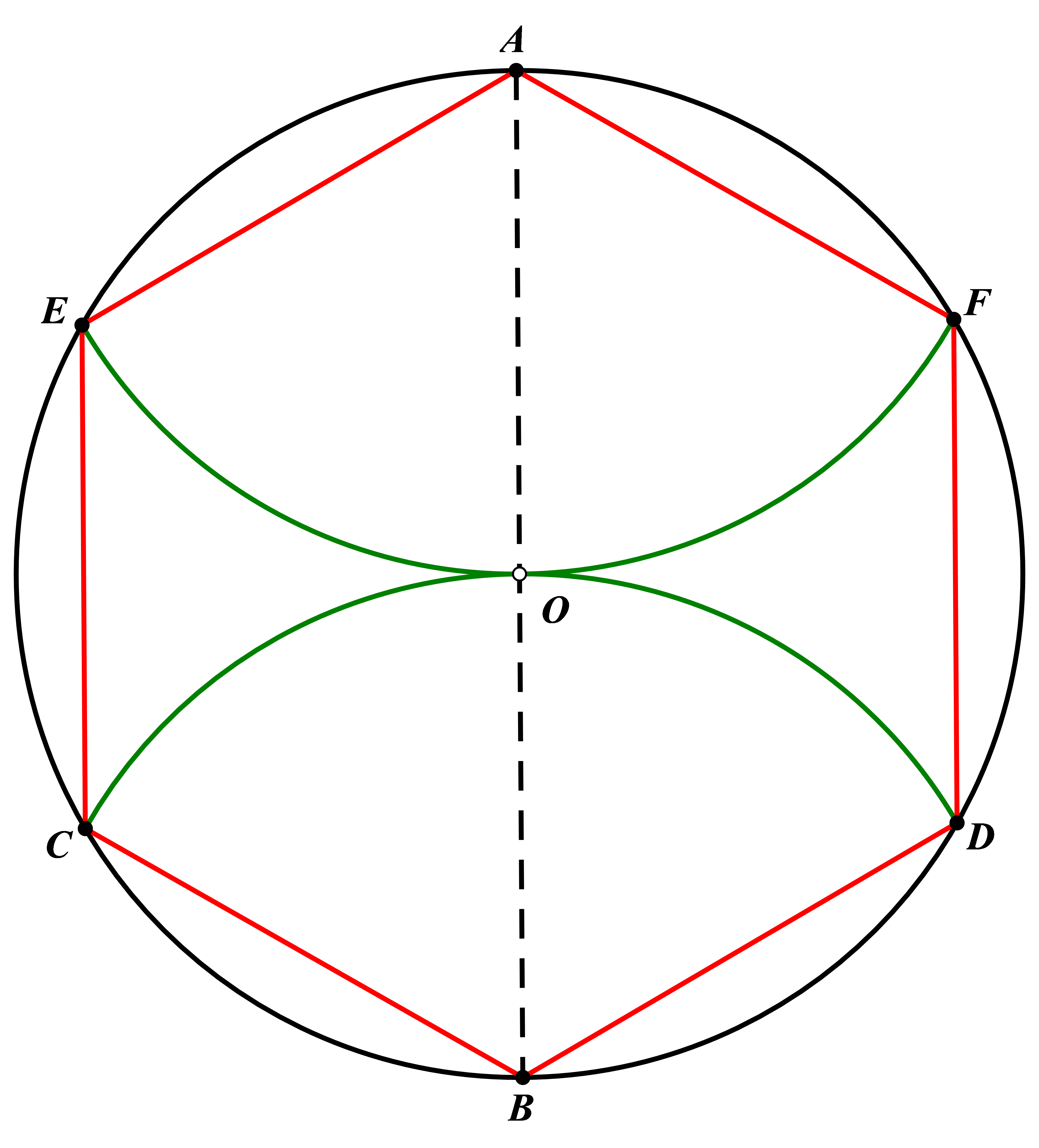
Figure 2. Method

Passing through the center of the circle O, draw any diameter AB. With A as the center and AO as the radius, draw an arc intersecting the circumference at points E and F. With B as the center and BO as the radius, draw an arc intersecting the circumference at points C and D. Connect the points on the circumference in clockwise order; AFDBCE will form an inscribed regular hexagon within the circle.

Principle: It can be easily verified that the arcs AE, EC, CB, BD, DF, and FA correspond to central angles of 60°, hence AE = EC = CB = BD = DF = FA = R (where R is the radius of the circle).

2.2. Quadrisection and Octant Division of a Circle

2.2.1. Quadrisection

Passing through the center of the circle O, draw any diameter AB. With A as the center and AB as the radius, draw a circle, and simultaneously with B as the center and BA as the radius, draw another circle. The two circles intersect at points E and F. Connect EF, which intersects circle O at points C and D. ACDB is then an inscribed square within the circle.

Principle: This method involves drawing the perpendicular bisector of AB, which is CD. At this point, the arcs AC, CB, BD, and DA correspond to central angles of 90°. It is clear that ACDB is a square.

Figure 3. Method

2.2.2. Octant Division

On the basis of dividing the circle into four equal parts, connect and construct the perpendicular bisectors of segments AC, CB, BD, and DA, which intersect the circle at points M, P, Q, and N, respectively. Connect the points on the circumference in clockwise order; ANDOBPCM will form an inscribed regular octagon within the circle.

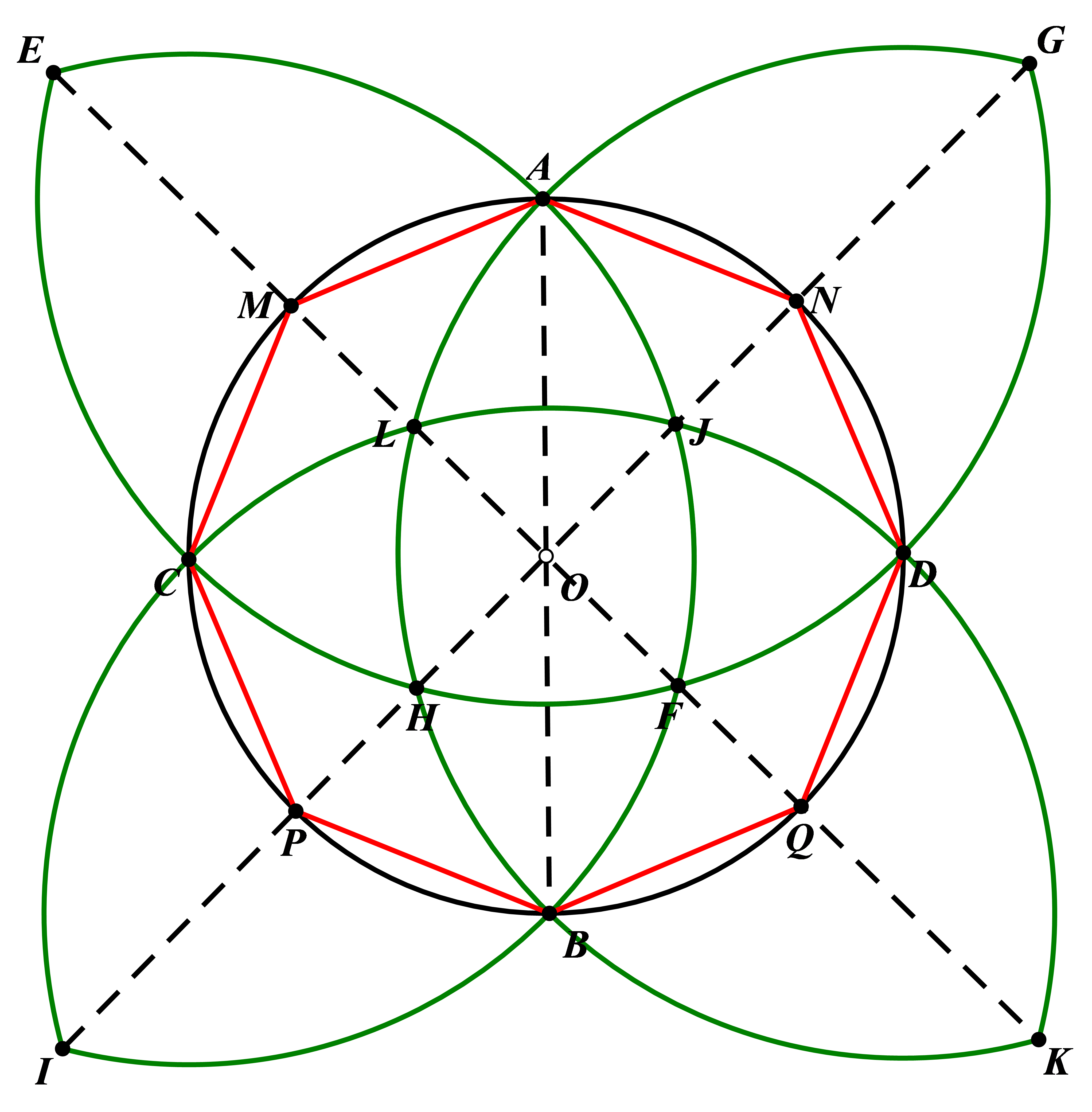
Figure 4. Method

Principle: This method involves bisecting each arc segment, making the central angles corresponding to the adjacent vertices of the octagon 45°. As a result, the octagon obtained is naturally a regular octagon.

3. Pentagon and Decagon Division of a Circle

Pre-knowledge: The side length of an inscribed regular decagon is \( \frac{\sqrt[]{5}-1}{2}R \) .

3.1. Decagon Division:

Using a ruler and compass, construct the figure AB \( ⊥ \) CD. Find the midpoint E of OD, and connect AE. With E as the center and EO as the radius, draw an arc intersecting AE at point F. With A as the center and AF as the radius, draw an arc intersecting circle O at point G. Connect AG to form one side of the decagon. Then, starting from point G, use GA as the radius to successively construct arcs along the circumference of the circle, dividing the circle into 10 equal parts. Finally, connect these points in a clockwise direction; ANMLKBIIHG will form the inscribed regular decagon within the circle.

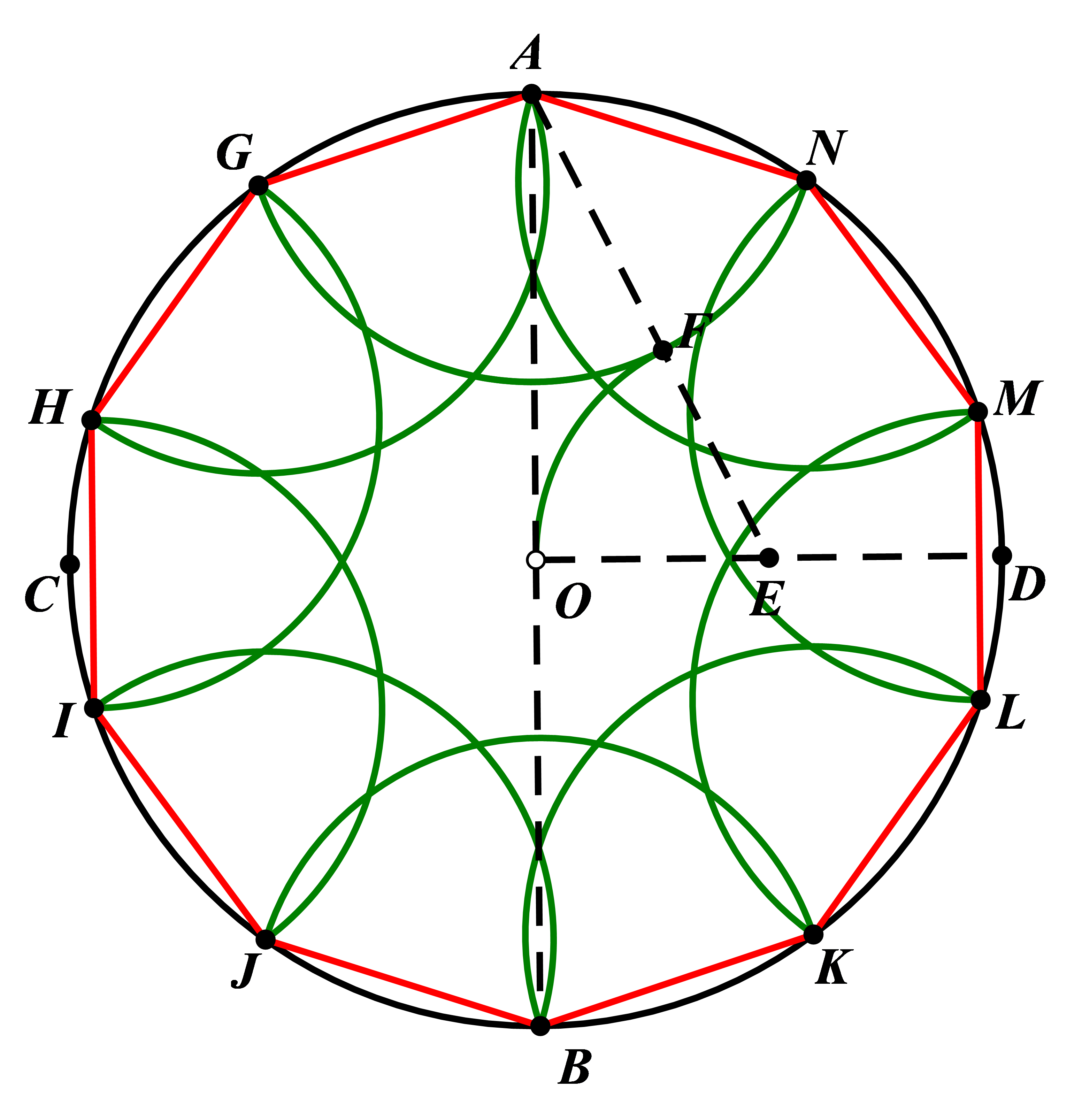
Figure 5. Method

Principle Since OA equals R and EO equals \( \frac{R}{2} \) , therefore AE equals \( \frac{\sqrt[]{5}}{2}R \) . Also, because EF equals EO equals \( \frac{R}{2} \) , this implies that AF equals \( \frac{\sqrt[]{5}-1}{2}R \) . Furthermore, AG equals AF, which means the shape constructed is a regular decagon.

3.2. Division into five equal parts:

By connecting the vertices of the inscribed regular decagon of the circle in sequence, you can obtain AHJKM as an inscribed regular pentagon within the circle.

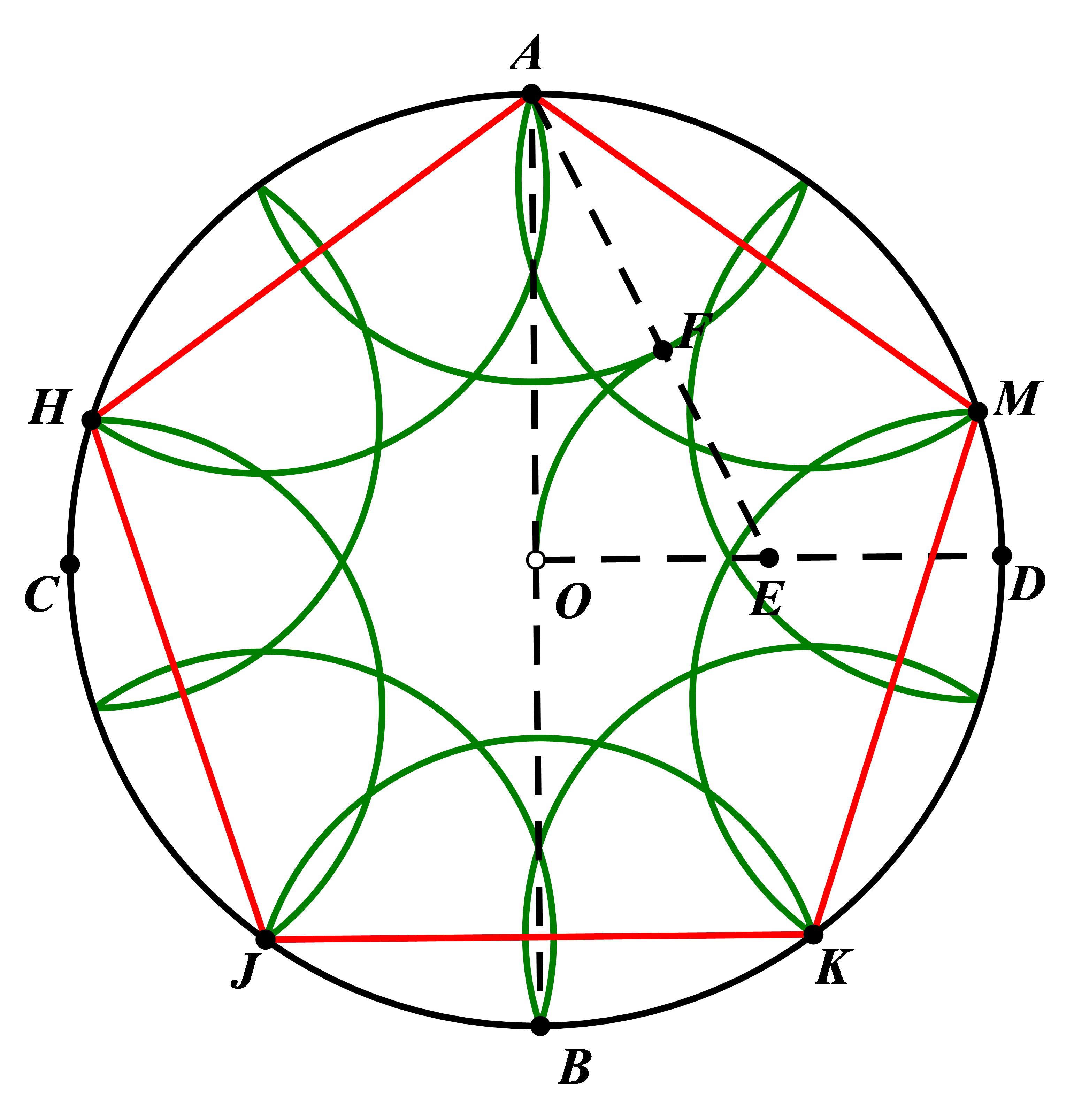
Figure 1. Method

Principle: Since the arc length corresponding to each side is 72°, the resulting figure is a regular pentagon.

3.3. Division of the circumference into fifteen equal parts:

First, draw two perpendicular radii A0 \( ⊥ \) B0, take the midpoint C of OB, connect AC, and draw an arc with point C as the center and CO as the radius, intersecting AC at point D; draw an arc with point A as the center and AD as the radius, intersecting circle O at point E; draw an arc with point A as the center and AO as the radius, intersecting circle O at point F. EF is a side of the inscribed regular pentadecagon (15-gon), and by successively measuring from EF along the circumference, you can obtain \( EFGHIJKLMNPQRST \) as the inscribed regular pentadecagon.

Principle: Clearly, the central angle corresponding to AF is 60°, and the central angle corresponding to AE is 36°, so the central angle corresponding to EF is 24°, which meets the condition for a regular pentadecagon.

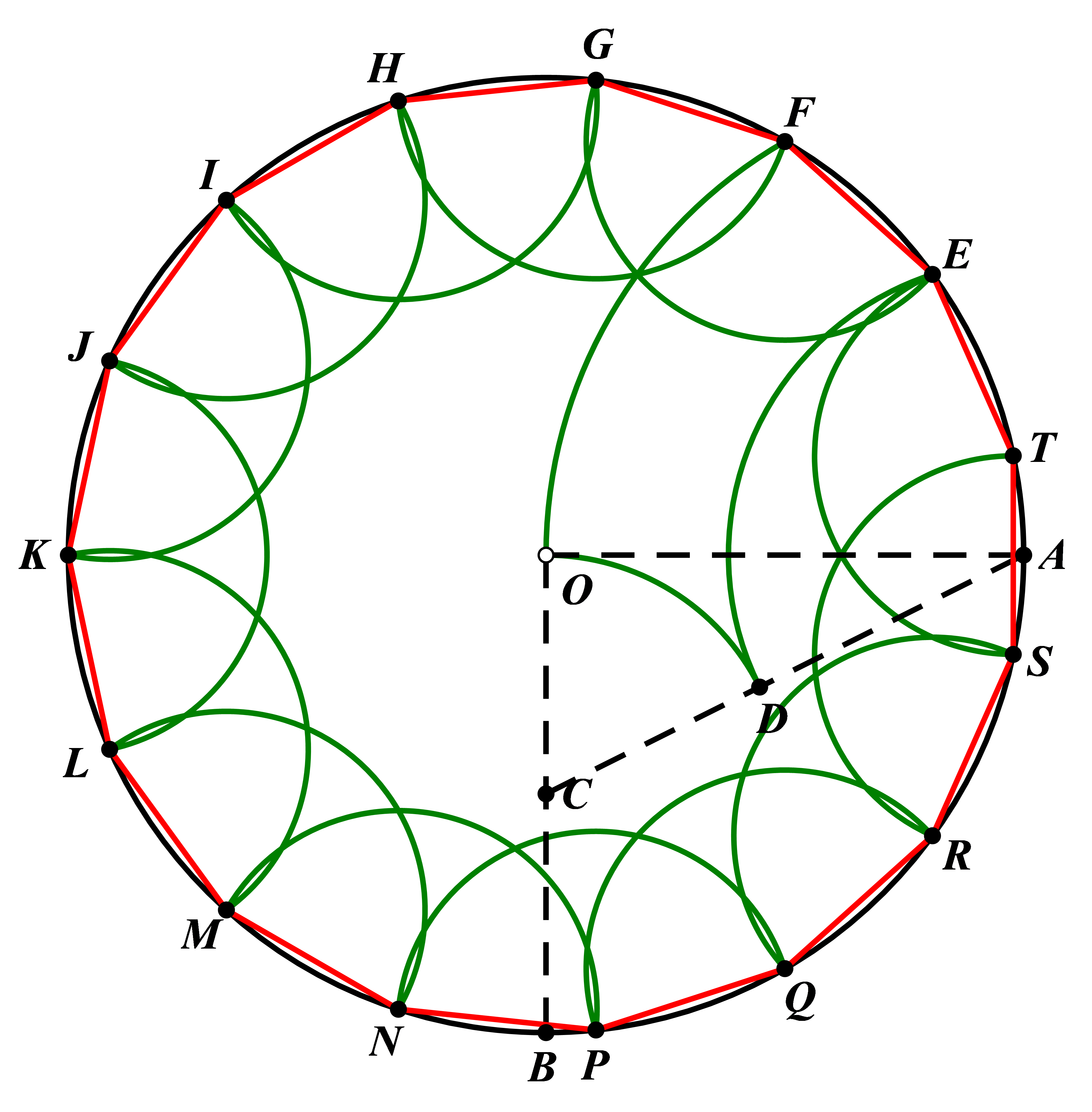
Figure 2. Method

4. Approximate Division of the Circumference into Equal

4.1. Approximate Division of the Circumference into Seven Equal Parts

Choose any point P on circle O, and draw an arc with P as the center and PO as the radius, intersecting circle O at points A and B. Connect AB and let it intersect PO at point C. Draw an arc with point A as the center and AC as the radius, intersecting circle O at point D, and connect AD. At this point, AD is one side of an approximate regular heptagon (7-gon).

Principle: It is easy to know that triangles OAP and AOBP are equilateral triangles, so AO = R, OC = \( \frac{R}{2} \) , and AD = AC = \( \frac{\sqrt[]{3}}{2}R \) . Let's assume the central angle corresponding to AD is \( 2θ \) , \( sinθ=\frac{AD}{2R}=\frac{\sqrt[]{3}}{4}=0.43301 \) . Therefore, 20 degrees is 51°19'4". In theory, the central angle for a regular heptagon is \( 51^{°}25^{ \prime }43^{ \prime \prime } \) , and the error is \( 51^{°}19^{ \prime }4^{ \prime \prime }-51^{°}25^{ \prime }43^{ \prime \prime }=-6^{ \prime }39^{ \prime \prime } \) (an underestimation approximation).

Figure 3. Method

4.2. Approximate Division of the Circumference into Nine Equal Parts

Choose any point P on circle O, and draw an arc with P as the center and PO as the radius, intersecting circle O at points A and B. Connect AB and let it intersect PO at point C, then extend CB to point D such that CD equals R; draw an arc with C as the center and CD as the radius, and another arc with D as the center and DC as the radius, the two arcs intersect at point E. Connect OE, and let it intersect circle O at point F. BF is then one side of an approximate regular nonagon (9-gon).

Principle: Let ∠COE = β. It is clear that ∠PCE = 30°, so ∠CEO = 30° - β. According to the Law of Sines, we get \( \frac{OC}{sin∠CEO}=\frac{CE}{sin∠COE} \) , so we get \( tanβ=\frac{\sqrt[]{3}-1}{2} \) , which gives β = \( 20^{°}6^{ \prime } \) . Therefore, ∠FOB = 39°54'. Since CE = sin(∠CEO) and sin(∠COE), and theoretically, the central angle for each side of a regular nonagon is 40°, the error is \( 39^{°}54^{ \prime }-40^{°}=-6^{ \prime } \) (an underestimation approximation).

,

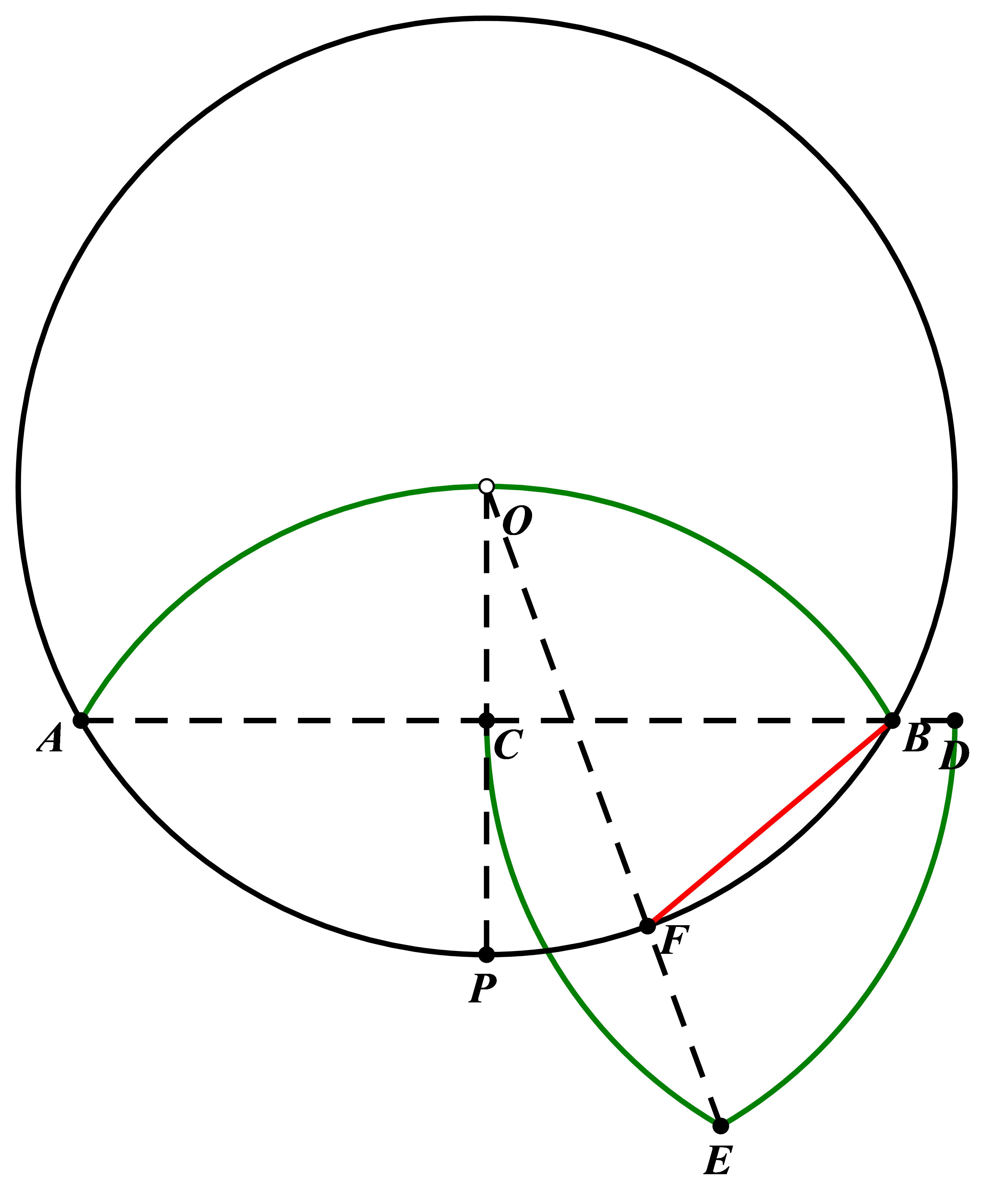
Figure 9. Method

4.3. Approximation of a Regular n-gon Inscribed in a Given Circle (Taking a Regular 11-gon as an Example), [Tobi's Method]

Divide the diameter of circle O into n equal parts (taking n=11 as an example). With 1 and 12 as centers, draw arcs using the diameter of circle O as the radius; the two arcs intersect at point P. Connect PO and extend it to intersect circle O at point a. Then, take a point Q on the diameter such that the length of OQ is \( \frac{2}{n} \) of the diameter's length, connect PQ and extend it to intersect circle O at point b. Connect ab, and ab will be a side of the inscribed regular n-gon (in this case, n=11).

Principle: First, derive the error formula for this method:

Let ∠bPO = α, ∠PbO = β, then ∠bOa = α + β.

(1) To find α: In the middle, Since

OP = \( \frac{\sqrt[]{3}}{2}n \) , OQ = 2,

so

PQ = \( \sqrt[]{2^{2}+(\frac{\sqrt[]{3}}{2}n)^{2}} \) , \( sinα=\frac{OQ}{PQ}=\frac{4}{\sqrt[]{16+3n^{2}}} \) .

(2) To find β: Because

Ob = \( \frac{n}{2} \) ,

and

\( \frac{OP}{sinβ}=\frac{Ob}{sinα} \) ,

substitute sinα to get

sinβ = \( \frac{4\sqrt[]{3}}{\sqrt[]{16+3n^{2}}} \) .

Figure 4. Method

Therefore,

\( ∠aOb=α+β=arcsin\frac{4}{\sqrt[]{16+3n^{2}}}+arcsin\frac{4\sqrt[]{3}}{\sqrt[]{16+3n^{2}}} \)

Taking the sin on both sides, we get,

\( sin∠aOb=\frac{4}{\sqrt[]{16+3n^{2}}}\sqrt[]{1–\frac{48}{16+3n^{2}}}+\frac{4\sqrt[]{3}}{\sqrt[]{16+3n^{2}}}\sqrt[]{1–\frac{16}{16+3n^{2}}} \)

\( ∠aOb=arcsin4\frac{(\sqrt[]{3n^{2}–32}+3n)}{3n^{2}+16} \)

Thus, we have the error =

\( arcsin4\frac{(\sqrt[]{3n^{2}–32}+3n)}{3n^{2}+16}–\frac{360^{°}}{n} \)

We can calculate the corresponding error for different numbers of sides: n

Table 1. Results of calculation

Therefore, when \( n \gt 9 \) , the error is smaller.

5. Summary

In the above text, we have studied the problems of exact and approximate division of the circumference of a circle. The most critical aspect is to accurately determine the corresponding central angles and use compass and straightedge to solve the problems. In the process of solving, we have deeply appreciated the subtlety of compass and straightedge drawing and the expansion of thinking. Of course, there are still many methods in the approximate division of the circumference that await exploration. How to optimize and expand them is the direction and goal for future research.