1 Introduction

In recent years, the demand for poultry products has significantly increased due to global population growth and changes in dietary structures [1]. As an essential agricultural production unit, the operational management of chicken farms is directly linked to the sustainable development of the agricultural economy [2]. However, traditional farm management methods largely rely on experience and lack systematic quantitative analysis and scientific optimization techniques, making it difficult to address the challenges posed by market price fluctuations and resource limitations [3][4]. Therefore, exploring a scientific method capable of optimizing chicken farm operations in a dynamic market environment holds significant practical value [5].

This paper aims to investigate how to maximize the economic benefits of chicken farms through mathematical modeling. First, we establish a profit optimization model for farms based on integer programming theory, considering the proportion of roosters, hens, and chicks. Next, the branch-and-bound method is used to solve the model and determine the optimal allocation of chickens under different market price conditions [6][7]. We then conduct a detailed analysis of the model’s results, exploring the impact of market price fluctuations on farm operations and proposing corresponding operational strategy recommendations [8]. Finally, the effectiveness of the model is verified using actual data, providing theoretical support and practical guidance for the scientific management of chicken farms.

2 Establishing the profit model for chicken farms based on integer programming

Chickens on farms can be categorized into chicks, roosters, and hens. Depending on their purpose, roosters can be further divided into broilers and breeding roosters, while hens can be categorized as laying hens and breeding hens [9]. The breeding and renewal process of chickens on farms is shown in Figure 1. In this paper, an integer programming model is employed to adjust the proportional allocation of the four types of chickens, aiming to maximize the farm’s profit.

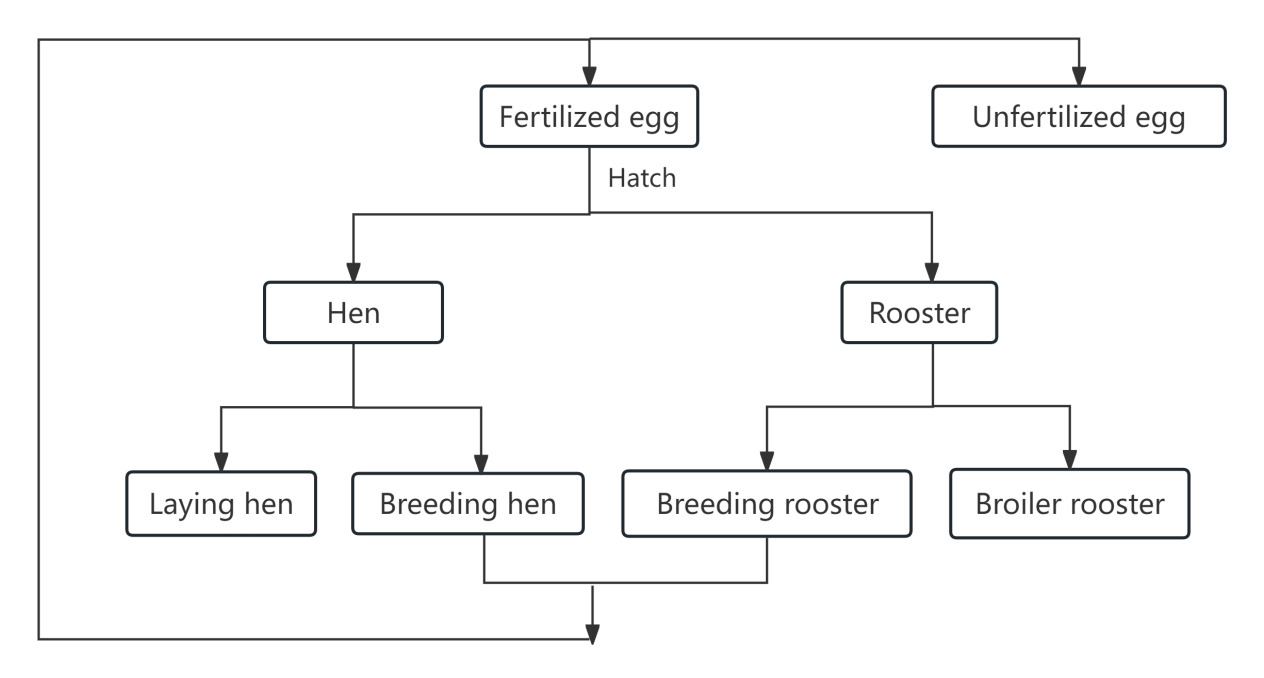
Figure 1. The Breeding and Renewal Process of Chickens on Farms

In this paper, we assume that the number of broilers among the roosters is denoted as \( c_{11} \) , the number of breeding roosters as \( c_{12} \) , and the number of breeding roosters in the growth phase as \( c_{13} \) . Among the hens, the number of laying hens is \( c_{21} \) , the number of breeding hens is \( c_{22} \) , and the number of breeding hens in the growth phase is \( c_{23} \) . For chicks, the number of male chicks is \( c_{31} \) and the number of female chicks is \( c_{32} \) . We also assume the number of fertilized eggs in stock is \( c_{42} \) , where it is assumed that all the eggs laid by the breeding hens are fertilized. Let the selling price corresponding to the above variables be \( m_{ij} \) yuan per unit (for \( i=1,2;j=1,2 \) ), the feed cost be \( d_{ij} \) yuan per unit (for \( i=1,2;j=1,2 \) ), the growth cycle be \( g_{ij} \) days (for \( i=1,2;j=1,2 \) ), and the time invested per day by employees in caring for different types of chickens be \( t_{ij} \) hours (for \( i=1,2;j=1,2 \) ).

Assuming the farm’s monthly revenue is \( Q \) , based on the above variables, it can be calculated as:

\( Q=\sum_{i=1,2,3}\sum_{j=1,2}\frac{c_{ij}∙m_{ij}}{g_{ij}}-\sum_{j=1,2,}\sum_{k=1,2}\frac{c_{jk}∙m_{3j}}{g_{jk}}+c_{21}∙u∙m_{41} \) (1)

Assuming the farm’s monthly cost is \( D \) , it can be expressed as:

\( D=\sum_{i=1,2}\sum_{j=1,2,3}c_{ij}∙d_{ij}+\sum_{j=1,2}c_{3j}∙d_{3j}+\frac{c_{42}∙d_{42}}{g_{4}}+T∙s∙m+d_{s} \) (2)

where \( g_{4} \) is the incubation time for each egg, \( T \) is the maximum working hours per day for each employee, \( s \) is the hourly wage for each employee, \( m \) is the number of employees employed by the farm, and \( d_{s} \) represents other potential costs incurred during the farming process, such as disinfection, sanitation, and vaccination [10].

Since the total time employees spend on each type of chicken per day cannot exceed their maximum daily working hours, the following constraint applies:

\( \sum_{i=1,2,3}\sum_{j=1,2}c_{ij}∙t_{ij}+c_{42}∙t_{4}≤T \) (3)

In addition, the number of fertilized eggs should be greater than the number of chicks produced daily. Thus,

\( \sum_{j=1,2}\frac{c_{3j}}{g_{3j}}≤c_{22}∙u \) (4)

To ensure the sustainable development of the chicken population on the farm, the number of chicks produced daily should exceed the number of broilers, laying hens, and breeding chickens consumed daily. Therefore:

\( \begin{cases}\sum_{j=1,2}\frac{c_{1j}}{g_{1j}}≤\frac{c_{31}}{g_{31}} \\ \sum_{j=1,2}\frac{c_{2j}}{g_{2j}}≤\frac{c_{32}}{g_{32}}\end{cases} \) (5)

According to the literature, the ratio of male to female chicks hatched is approximately 1:1, that is, \( c_{31}=c_{32} \) ; the breeding ratio of roosters to hens is about 1:13, that is, \( c_{12}:c_{22}=1:13 \) .

Based on the above analysis, a linear programming model can be constructed to solve the profit maximization problem for chicken farming.

\( Max Q-D=\sum_{i=1,2,3}\sum_{j=1,2}\frac{c_{ij}∙m_{ij}}{g_{ij}}-\sum_{j=1,2,}\sum_{k=1,2}\frac{c_{jk}∙m_{3j}}{g_{jk}}+c_{21}∙u∙m_{41}-\sum_{i=1,2}\sum_{j=1,2,3}c_{ij}∙d_{ij}-\sum_{j=1,2}c_{3j}∙d_{3j}-\frac{c_{42}∙d_{42}}{g_{4}}-T∙s∙m-d_{s} \)

s.t. \( \begin{cases}\sum_{i=1,2,3}\sum_{j=1,2}c_{ij}∙t_{ij}+c_{42}∙t_{4}≤T \\ \sum_{j=1,2}\frac{c_{3j}}{g_{3j}}≤c_{22}∙u \\ \sum_{j=1,2}\frac{c_{1j}}{g_{1j}}≤\frac{c_{31}}{g_{31}} \\ \sum_{j=1,2}\frac{c_{2j}}{g_{2j}}≤\frac{c_{32}}{g_{32}}\end{cases} \)

3 Model solution and result analysis

The integer programming model mentioned above can be solved using the branch-and-bound method. The branch-and-bound method relaxes the integer solution condition of the original problem, decomposing it into several sub-problems, and solving each one individually. If the optimal solution of any sub-problem is a feasible solution to the original problem, it becomes the optimal solution, and the calculation ends [6][11]. Otherwise, the value of its objective function becomes a new upper bound for the original problem, and branching continues. The flowchart of this process is shown in Figure 2.

Figure 2. Flowchart of the Branch-and-Bound Method

Using the branch-and-bound method, the above model was solved with MATLAB software. Based on the solution results, different prices for broilers and chicks correspond to different optimal solutions. The table below shows the maximum total profit the farm can achieve and the corresponding stocking quantity for each chicken product under various broiler and egg price conditions, assuming a total workforce of 100 employees.

Table 1. Optimal Solutions as Market Prices Change

It is evident that the optimal stock levels of different chicken types in the farm, when achieving maximum profit, are related to factors such as broiler prices and chick prices. Therefore, adjustments to the farm’s scale should be made in response to changes in their market prices.

4 Recommendations for the poultry farm based on model results

Based on the model above, we analyze the sales conditions of poultry farms in the Weifang region of Shandong over different periods within the past year. The following table shows the market sales prices for broilers, eggs, and chicks during three different periods.

Table 2. Sales Prices of Broilers, Eggs, and Chicks

Figure 3 illustrates the poultry farming situation in Weifang, Shandong Province on a specific day in March 2024. The left graph shows the relationship between the number of employees hired, costs, revenue, and profit, while the right graph depicts the relationship between the number of employees and the optimal number of chickens. From these figures, it can be observed that in March, the price of chicks in Weifang was relatively high. Therefore, the farm was more inclined to sell chicks rather than raising them to broilers for sale.

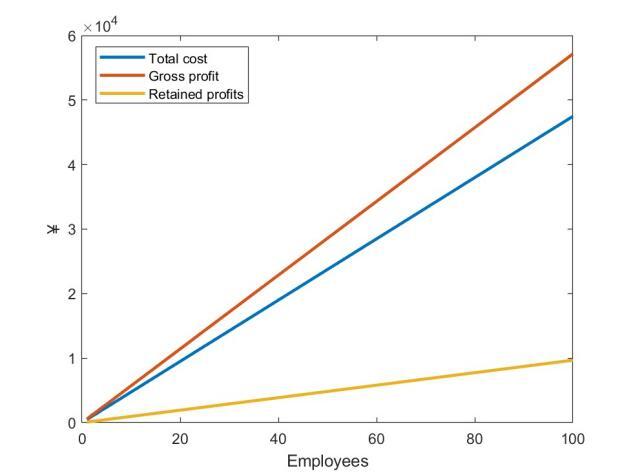
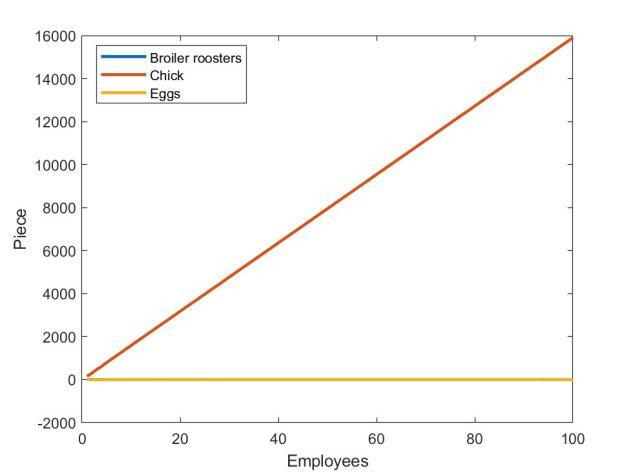
Figure 3. Profit Analysis of the Poultry Farm in March

Figure 4 presents the poultry farming situation in Weifang, Shandong Province on a specific day in June 2024. Due to the relatively low price of chicks in June, selling broilers offered greater profit potential than selling chicks. At this time, the farm focused on raising more broilers to maximize profits. Since the ratio of male to female chicks is 1:1, and the number of chicks required for maintaining generational renewal of breeding roosters and hens is small, the farm chose to raise all male chicks as broilers and sell the remaining chicks. As a result, the number of broilers sold was nearly equal to the number of chicks sold.

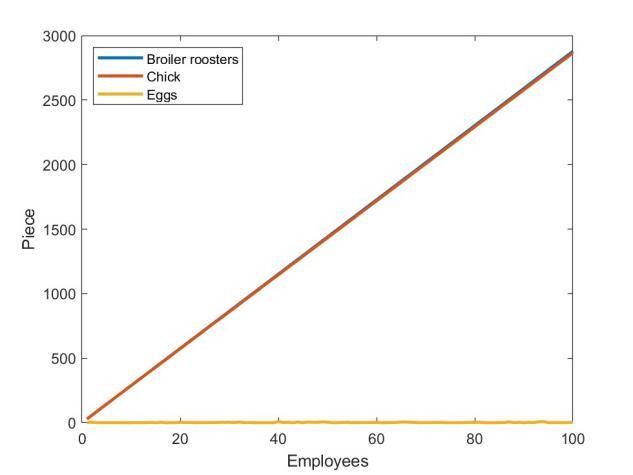
Figure 4. Profit Analysis of the Poultry Farm in June

Figure 5 analyzes the poultry farming situation in Weifang, Shandong Province on a specific day in September 2024. As chick prices were high in September, the model predicts that selling chicks directly would yield the highest profit. The poultry farm remained profitable in the September market, and with the expansion of the farm’s scale, overall profits increased accordingly.

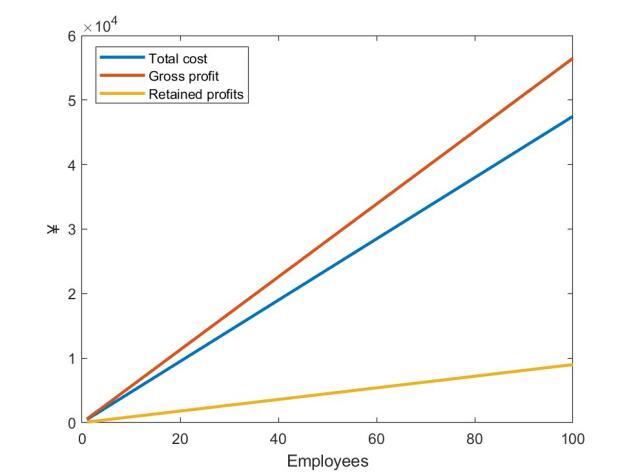
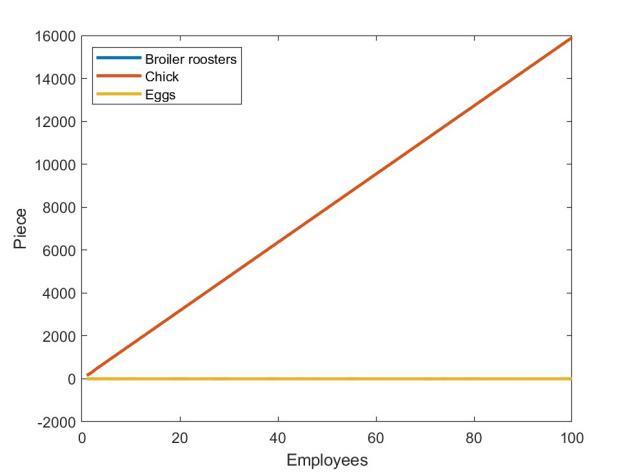
Figure 5. Profit Analysis of the Poultry Farm in September

Based on the above analysis, poultry farms should adjust their sales strategies flexibly according to market prices. Additionally, when the farm is in a profitable state, expanding the farm’s scale and hiring more employees could further increase profits.

Authors’ contributions

The two authors contribute to this work equally.