1. Introduction

Peer-to-Peer (P2P) lending emerged in the 21st century as an innovative online lending model, rapidly expanding globally since its 2005 UK inception and its 2007 rise in China. Despite its benefits, the rapid growth led to significant systemic risks, with a large proportion of platforms becoming problematic by 2018, underscoring the critical need for robust risk management. This necessity has driven a shift in academic research towards integrating big data and machine learning algorithms for credit risk assessment, moving beyond traditional financial models to encompass interdisciplinary approaches. Recognizing the increasing role of P2P platforms as credit intermediaries, this paper addresses the vital need for effective borrower default prediction. We collected approximately one million loan records from the Renrendai platform using a web crawler, developed a Back-Propagation (BP) neural network model, and achieved over 85% prediction accuracy. Then, we further enhanced the model by generating ROC curves and introducing a novel "SPACE" indicator to determine the optimal prediction threshold for operational risk mitigation. This research thus provides a refined credit evaluation model for P2P lending, offering practical insights for managing its inherent risks.

2. Literature review

The rapid expansion of Peer-to-Peer (P2P) lending platforms has introduced novel financial opportunities, yet it concurrently presents a significant challenge in managing inherent high default risks due to factors like information asymmetry and the absence of traditional financial intermediaries [1]. Early research in P2P credit risk assessment explored various statistical and machine learning models, with studies by Lopez [2] applying Gaussian mixture models to identify the compensatory role of social identity. Luo further proposed effective Kernel-based models. Researchers also began integrating diverse factors, such as the "Wisdom of Crowds" [3] and the influence of images on lender behavior [4]. Further advancements saw linear regression models exploring macro-level factors like country and currency [5], alongside early applications of ensemble methods [6] like Random Forest [7] for borrower credit scoring, underscoring a trend on data-driven approaches to predict credit risk.

Building upon these foundational explorations, the field has increasingly adopted sophisticated machine learning techniques to enhance default prediction accuracy. Modern studies frequently employ a range of methods including logistic regression, support vector machines, and particularly, neural networks and advanced ensemble techniques like XGBoost [8, 9, 10]. These models consistently demonstrate superior predictive power over traditional credit assessment tools and internal platform grading systems, often achieving high AUC scores [10]. Key determinants of default consistently identified across studies include loan amount, debt-to-income ratio, annual income, loan term, and credit grade [8, 10]. Furthermore, research highlights the importance of incorporating non-traditional data sources, such as linguistic cues from loan applications [1], and emphasizes the value of transparent information disclosure in mitigating risk at the platform level [11].

Our research contributes to the literature by developing a BP neural network model for P2P borrower default prediction using a unique dataset from Renrendai platform.

3. Research methodology and data

3.1. Data

3.1.1. Data acquisition and processing

This study utilized loan order data from the Renrendai website, obtained via a web crawler, initially comprising 59 indicators per order. Renrendai is one of the earliest Peer-to-Peer (P2P) lending platforms developed in China, with a relatively well-established information disclosure mechanism and strong risk control capabilities. The raw data includes a series of indicators such as total loan amount, annual interest rate, repayment period, and guarantee method. Obviously, some indicators, such as the guarantee method, have negligible impact on whether the borrower can successfully repay the loan. Secondly, among the large number of orders initially crawled, there are also some unsuccessful loan orders and unexpired orders, which lack the dependent variable required for our modeling research and are therefore not included in this study. Considering the above situations, the crawled data is processed in the following three steps: First, all successful loan orders are filtered out. The order information disclosed by Renrendai is arranged according to the order application number, including both successful and unsuccessful loan orders. Here, only successful loan orders can be used as historical data for fitting the credit default model, thus unsuccessful loan orders and uncompleted orders (those that have not yet reached the final repayment date) are removed. Second, the latest order information for each user is filtered out. Based on the characteristics of Renrendai's dynamic database (where all completed orders for each user display the user's latest personal information), in the first step of processing, all orders for each user are selected, past orders are deleted, and only the latest order information for each successful loan user is retained. Furthermore, among the obtained indicators, those with a strong influence on default are selected. From the 59 obtained indicators, 25 indicators considered to have an impact on credit default are chosen as output layer variables. Through the steps above, a total of 34,013 valid order data entries were filtered out.

3.1.2. Data labeling

The raw data, comprising one dependent variable and 25 independent indicators, will be quantified by assigning numerical labels to textual information based on its inherent degree. To optimize the performance of the Back-Propagation (BP) neural network model, which can experience reduced accuracy with an excessive number of input layer nodes, only these 25 indicators were selected for analysis.

Default status for a user's latest loan order will be determined by combining two key variables: severe delinquency and principal and interest to be repaid. Given that the weights within a neural network model do not possess direct economic interpretation, and the method of indicator quantification has minimal impact on the model's economic meaning or result interpretation, this section provides a concise overview of the indicator quantification process in Table 1.

3.1.3. Data dimensionality reduction

In neural network models, an excessive number of input layer neurons can significantly reduce prediction accuracy. Furthermore, considering that some of the 25 indicators in section 3.1.2 redundantly describe the borrower’s characteristics in certain aspects, we integrated and performed dimensionality reduction on these 25 indicators, resulting in a new set of 15 indicators for subsequent model solving and analysis. The data dimensionality reduction scheme is summarized in Table 2 as below.

The original dataset contains 25 potentially interdependent indicators that may collectively suffer from the curse of dimensionality. To improve model performance while preserving critical information, we implemented a targeted dimensionality reduction strategy through multiplicative integration of related feature-verification indicator pairs.

Taking age (Q2) and identity verification (Q14) as an illustrative example, we constructed a new composite indicator C2 through the operation Q2×(Q14+1). This formulation serves two important purposes. First, it naturally scales the reliability of age information based on verification status: unverified age data (Q14=0) maintains its baseline value, while verified age data (Q14=1) receives enhanced weighting due to the increased credibility from identity documentation. Second, the additive term ensures the preservation of original age information even in the absence of verification, preventing inappropriate nullification of potentially valid data.

This principled approach was systematically applied to other logically paired indicators, as detailed in Table 2. The resulting set of 15 composite indicators maintains the predictive power of the original features while reducing redundancy and improving computational efficiency. The specific multiplicative formulation for each indicator pair was chosen to appropriately reflect the relative importance and interaction effects between raw feature values and their corresponding verification statuses.

3.2. Model setting

The Back-Propagation (BP) neural network was implemented in MATLAB to predict loan default risk using Renrendai order data. As a widely adopted artificial neural network architecture, the BP network learns through backward error propagation to adjust internal weights [12, 13]. Prior to model construction, the dataset underwent comprehensive cleaning, classification, and feature selection. The network architecture was configured with 15 input nodes (corresponding to the reduced feature set), 5 hidden nodes (determined empirically), and 1 output node. A binary classification threshold of 0.5 was applied, where the output variable Y = 0 indicates default status and Y = 1 represents non-default status.

The sample data was partitioned with 30% allocated for training (denoted as traind) and 70% reserved for prediction. Network training employed the quasi-Newton method, which demonstrated superior convergence properties during preliminary trials - consistently avoiding computational stagnation while rarely requiring the maximum specified iterations. The error threshold was bounded between 0.0001 and 1, with a maximum of 1000 iterations permitted for convergence testing. Both training and testing datasets were subsequently processed through the network for model training and predictive validation. This implementation balanced computational efficiency with predictive accuracy, as evidenced by the network's stable convergence behavior during multiple test runs.

Given data imbalance in P2P lending, our focus extended beyond overall accuracy to specifically enhance default prediction. We used ROC and introduced a novel indicator, SPACE, to determine the optimal threshold. This weighted distance metric, calculated as:

$SPACE=[0.95(1-rateforbad{)}^2+0.05(1-rateforgood{)}^2{]}^{0.5}$(1)

Such a formula prioritizes minimizing errors in identifying bad borrowers (borrowers with default). The threshold corresponding to the minimum SPACE value on the ROC curve is considered optimal.

4. Results

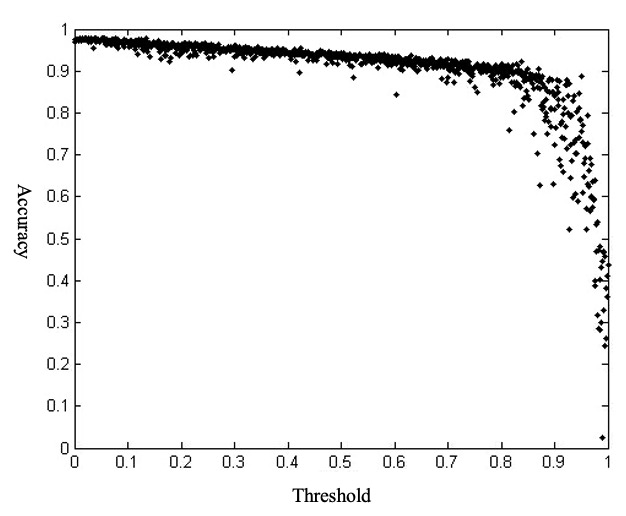
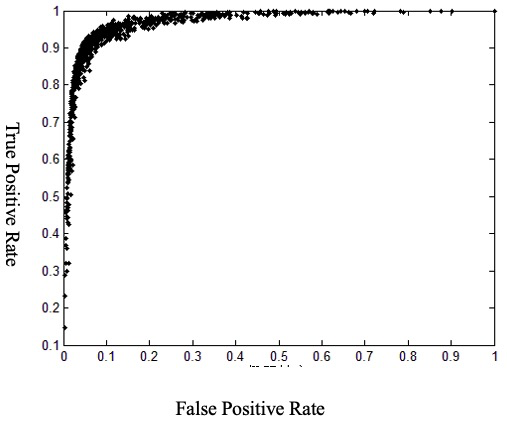
The prediction results and the model’s ROC are shown in Figure 1 and Figure 2, respectively. It can be viewed from Figure 1 that with the default threshold as 0.5

Figure 2 illustrates the non-uniform relationship between the True Positive Rate (TPR) and False Positive Rate (FPR) as the classification threshold varies. Our objective is to optimize the TPR, even if it entails a slight increase in false rejections. To achieve this, the SPACE indicator is employed to determine the optimal threshold interval. First, for each point in Figure 2, we calculate the Euclidean distance to the ideal point (0, 1), denoting this minimum distance as x. Second, the optimal SPACE reference interval is defined as [x,2x], with points falling within this range assigned a value of 1 and others 0. Third, the [0, 1] interval is divided into ten equal sub-intervals (e.g., [0, 0.1), [0.1, 0.2)), each containing 100 points given our 0.001 step size, and the proportion of points marked 1 within each sub-interval is calculated. Finally, the sub-interval with the highest proportion of points marked 1 is identified, and its midpoint is the optimal threshold. This process yields 1000 SPACE values, with probability distribution across intervals presented in Table 3.

A refined threshold was selected based on the analysis in Table 3, indicating an optimal range between 0.7 and 0.8. Consequently, 0.75 was chosen as the new threshold. Table 4 then presents a comparative analysis of the prediction performance of BP neural network model using this optimized threshold against the conventional 0.5 threshold.

As Table 4 illustrates, optimizing the threshold to 0.75 led to an 8.95% reduction in overall prediction accuracy. However, this adjustment also increased the true positive rate (identifying defaulted orders) by 5.49%, albeit at the cost of a 9.18% rise in the false positive rate. It is crucial to acknowledge the dataset's imbalance, characterized by a predominance of successfully repaid loans. Consequently, the increase in false positives has a more significant negative impact on overall accuracy than the positive effect of improved true positives.

Furthermore, given that some platforms provide principal guarantees, a single loan default results in costs exceeding the revenue from a successfully repaid loan. Persistent high default rates could also damage the platform's reputation, hindering long-term growth. Therefore, the BP neural network credit assessment model with a threshold of 0.75 is appropriate for financial risk management.

5. Discussion and conclusion

This paper constructs a P2P online lending credit evaluation model using the BP neural network algorithm. The model is then optimized by creating a SPACE indicator within the ROC curve, aiming to enable the model to identify more future defaulting orders (i.e., assess the credit status of borrowers currently posting loan requests) while sacrificing a certain number of creditworthy borrowers. Through the optimization of the algorithm's threshold, the model can achieve a default order identification accuracy of over 95%. This model has two main advantages. First, the model's prediction accuracy is high. The use of a neural network model means that the original economic significance of parameters is disregarded in favor of mathematical conclusions. This is highly significant for lending platforms whose goal is accurate identification rather than economic research. Second, while maintaining high accuracy, the model also considers the platform's operational revenue and costs. By constructing the weighted distance indicator SPACE, the model's ability to identify low-credit borrowers is enhanced.

However, the paper also has some shortcomings. For example, it does not address imbalanced data during the data selection phase, which blurs the principle behind the weight settings in the subsequent SPACE indicator. Additionally, the model fails to provide an economic analysis of the development of online lending platforms or P2P user behavior.

Future research can expand data collection by integrating loan data from more diverse domestic and international P2P platforms to improve model accuracy. Future efforts could employ algorithms like G-mean [13] and Acc [12], or explore models better suited for imbalanced datasets.