1. Introduction

The domain of recommendation systems, such as those employed for movie suggestions or online advertisements, has been witnessing a surge in interest and application. Traditional methodologies often revolve around A/B testing, a comparative analysis whereby different versions of the recommended items are presented to users [1]. During the test phase, the user base is partitioned, exposing half to one variant and the remaining half to an alternative. The winner of the test phase is implemented from then on. However, issues arise when determining the length of the test phase and averting the abrupt transition from exploration to exploitation [2]. This leads to the modern alternative – MAB Algorithms – that addresses the problem of making sequential decisions in an environment characterized by uncertainty.

The core inquiry central to MAB problem is which arm to pull at any given time, a task that grows increasingly intricate as the number of arms escalates. Several computational methodologies have been put forth to address this issue, among which the Explore-Then-Commit (ETC) algorithm is prominent. The ETC algorithm, a common and straightforward strategy, operates on the principle of initial exploration, where each ‘arm’ is tested a predetermined number of times. Subsequently, it transitions to the exploitation phase and commits to the ‘arm’ that demonstrated superior performance during the exploration stage. Despite its simplicity and widespread use, the optimal setting of the exploration phase with respect to specific datasets remains an open question and a challenge in diverse scenarios.

Previous studies have delved into the theoretical properties and optimality procedures of the ETC algorithm. For instance, Garivier et al. demonstrated that strategies encompassing an exploration phase followed by exploitation are necessarily suboptimal, while Jin et al. presented a bifurcated explore-then-commit algorithm, which includes two distinct phases of exploration and exploitation, and demonstrated its potential to attain an asymptotically optimal regret boundary [3, 4]. In the work [5], Yekkehkhany et al. highlighted that the arm with the greatest anticipated reward, while being the optimal selection for infinite exploitation rounds, may not invariably produce the highest reward in single or finite exploitation rounds. Instead, the authors suggest a shift in perspective towards risk-aversion, where the goal is to compete against the arm that offers the greatest trade-off between risk and reward.

These studies tend to focus on the enhancement of the algorithmic performance, centering on the balancing act between the exploration and exploitation phases and the subsequent consequences of reward maximization. However, the hyperparameter selection for the ETC algorithm using specific datasets has received relatively little attention in the existing literature, constituting a noticeable gap. This absence of comprehensive guidelines or robust methodologies for determining the hyperparameters in practical scenarios is where this study differs and aims to contribute. In particular, the optimal length of the exploration phase and horizon, crucial parameters in the ETC algorithm, are often left as a vague concept and is not thoroughly investigated, especially in relation to specific datasets or problem domains.

To solve the limitation mentioned above, this study aims to provide comprehensive guidelines for the application of the ETC algorithm in the context of movie recommendation systems by conducting a comprehensive empirical analysis using the MovieLens 1M Dataset. Such systems constitute a real-world problem of substantial practical importance, extending across various applications such as online decision-making applications and recommender systems. The empirical focus and contribution distinguish this work from previous studies, which have primarily focused on theoretical aspects of the ETC algorithm.

The structure of this paper is organized as follows: Section 2 offers an overview the MAB algorithm framework and further describes the ETC algorithm. In Section 3, the effect caused by the two parameters, the horizon and the number of times each arm is explored, on the effectiveness of the algorithm will be studied. Section 4 encapsulates the key findings of the paper and outlines potential areas for future research.

2. Method

2.1. Dataset description and preprocessing

In this study, the MovieLens 1M Dataset provided by the GroupLens research lab was used [6]. The dataset comprises of 1,000,209 million historical ratings of 3,883 movies by 6,040 unique users [6]. The dataset contains three files, ratings, users, and movies, with three, four, and five features respectively. Given that the objective of the MAB algorithm in this paper is to reduce cumulative regret by selecting the genre with the highest mean rating, the pertinent features required for this process include ‘MovieID’, ‘Genres’, and ‘Rating’.

The dataset does not have any missing values, which simplifies the preprocessing stage and avoids the need to make assumptions about the missing data. Moreover, since the variables are categorical or ordinal in nature (e.g., ratings on a scale of 1-5), it is unnecessary to treat outliers. The only additional preprocessing step is to handle the ‘Genres’ field. This is accomplished by merging the files ‘movies’ and ‘ratings’ based on ‘MovieID’. Subsequently, in cases where a movie encompasses multiple genres, such as ‘Action’ and ‘Adventure’, it becomes necessary to decompose the genres into separate entities. This entails generating distinct rows for each genre associated with the movie, resulting in one row denoting ‘Action’ as the genre and another row denoting ‘Adventure’. This approach facilitates the analytical and modeling processes at the granularity of individual genres, rather than considering movies as a unitary entity.

2.2. Multi-armed bandit algorithm framework

The MAB problem encapsulates a sequential decision-making process between an agent and an uncertain environment. Each time step, denoted by \( t \) , allows the agent to choose a bandit arm \( {A_{t}} \) from a set of \( k \) independent arms. The environment then reveals a reward \( {R_{t}} \) which is linked to the arm \( {A_{t}} \) following a 1-subgaussian distribution with an unknown mean value \( {μ_{{A_{t}}}} \) [4]. The objective is to select arms that yield the maximum cumulative reward over all \( n \) rounds, striking a balance between exploiting known good arms and exploring uncertain but potentially better ones [7]. Equivalently, the same objective can be articulated as the minimization of the cumulative regret over \( n \) rounds.

In a broader context, MAB algorithms demonstrate efficacy in facilitating agent learning across diverse contexts, including online recommendation systems, clinical trials, and network routing, where decisions must be made under uncertainty to maximize a certain objective [8–10]. The robustness of the MAB framework is rooted in its capacity to optimally balance exploration and exploitation, thereby fostering effective learning and strategic decision-making.

2.3. Explore-then-commit algorithm framework

The ETC algorithm operates by sampling each arm a predetermined number of times during the exploration phase, and subsequently exploiting the arm that demonstrated superior performance during this exploration. It is postulated that the reward distribution for all arms adheres to a 1-subgaussian distribution. There will be a total of \( n \) rounds, known as the horizon. For the dataset, each genre will be considered an arm, so \( k=18 \) . Let \( m \) be the number of times each arm will be explored. Then, the total exploration round would be \( m×k \) . The ETC algorithm framework is thus given below shown in Algorithm 1 [7].

The selection of the horizon \( n \) and \( m \) , the number of times each arm will be explored, as hyperparameters in the ETC algorithm is a strategic choice aimed at optimizing the balance between exploration and exploitation. The horizon sets the timeframe within which the algorithm operates. A longer horizon allows for more rounds of exploration and exploitation, potentially leading to a more accurate understanding of the reward distributions associated with each arm. Conversely, a shorter horizon necessitates quicker decisions but may result in less accurate estimations due to fewer data points. The hyperparameter \( m \) , which is directly proportional to the length of the exploration phase, is another critical parameter. A longer exploration phase allows the algorithm to gather more data about each arm, potentially leading to a more accurate estimation of the optimal arm. However, it also delays the exploitation phase, during which the algorithm leverages its knowledge to minimize cumulative regret. A shorter exploration phase hastens the onset of exploitation but risks making decisions based on incomplete information.

In the context of the ETC algorithm, adjusting these hyperparameters can influence cumulative regret, which measures the opportunity cost incurred by not always pulling the optimal arm. The cumulative regret is quantified as the aggregate of the sub-optimality gaps associated with arm \( i \) , where \( ∆i={μ^{*}}-{μ_{i}} \) [7]. In other words, the difference between the optimal mean reward and the mean reward of arm \( i \) . By systematically varying the horizon and the length of the exploration phase, this study aims to determine their impact on cumulative regret, thereby gaining insights into how to tune these parameters for optimal performance of the ETC algorithm for the MovieLens 1M dataset.

3. Results and discussion

The performance of the ETC algorithm with its respective parameters will be evaluated through a comparative analysis of the average cumulative regret each algorithm incurs up to its respective horizon. This paper has constructed two distinct experimental setups by manipulating the horizon ( \( n \) ) and the number of times each arm is explored ( \( m \) ) to scrutinize the performance of the ETC algorithms on the MovieLens dataset. The first experiment is designed to evaluate four distinct values of n, with each instance utilizing an exploration length that is 10% of the respective \( n \) . In the second experiment, each ETC algorithm is subjected to a series of ten trials for each exploration length. The average cumulative regret derived from these trials is graphically represented, accompanied by error bars indicating one standard deviation above and below this mean.

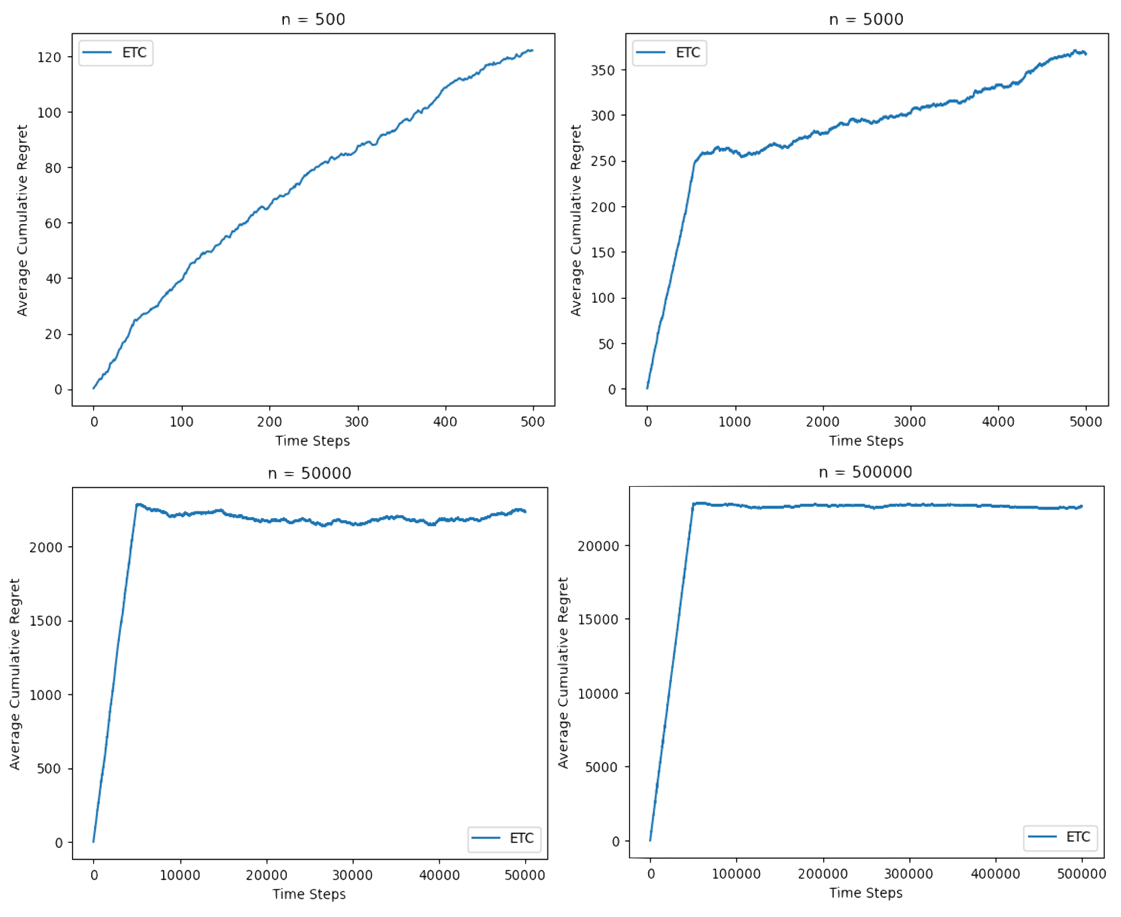
Figure 1. Performance of ETC algorithm for four different \( n \) values (Photo/Picture credit: Original).

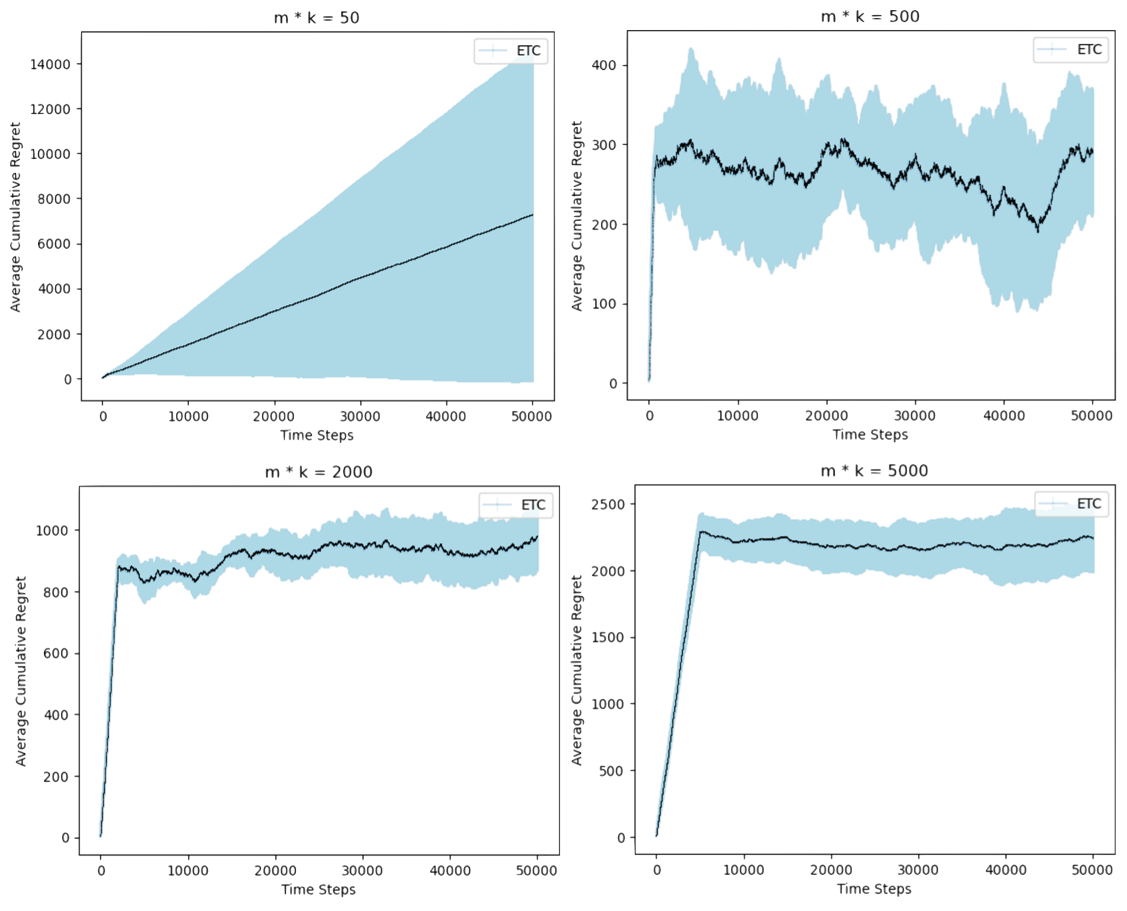
Figure 2. Performance of ETC algorithm for four different \( m \) values (Photo/Picture credit: Original).

As illustrated in Figure 1, the algorithm failed to identify the optimal arm at \( n=500 \) . This suboptimal performance is substantiated by the steadily increasing trend of the average cumulative regret as the number of time steps progresses. When the horizon is extended to \( n=5,000 \) , the ETC algorithm begins to display logarithmic regret behavior, indicative of improved performance. However, the graph still exhibits an upward trend for the average cumulative regret, suggesting that the algorithm is yet to reach its optimal performance. The most optimal value for the horizon is found to be \( n=50,000 \) . This is evidenced by a relatively stable trend in the average cumulative regret and a smaller cumulative regret in comparison to that of \( n=500,000 \) . This finding suggests that the ETC algorithm's performance improves significantly as the horizon increases, reaching an optimal point at \( n=50,000 \) before the performance starts to decline at \( n=500,000 \) .

In the second experiment, with a fixed horizon of \( n=50,000 \) rounds, the ETC algorithm exhibits superior performance when \( m×k \) , representing the optimal exploration length, equals 500. This is characterized by a smaller and more predictable error bar compared to the other graphs. Similar to Figure 1, with a for values of \( m×k \) less than 500, there is a noticeable decrease in the average cumulative regret as \( m×k \) increases shown in Figure 2. This suggests that increasing the exploration length within this range improves the algorithm's ability to identify the optimal arm. However, once \( m×k \) exceeds 500, the average cumulative regret begins to increase as \( m×k \) continues to rise. This indicates that a longer exploration length for the optimal arm (genre) beyond this point results in a higher cumulative regret, thus reducing the efficiency of the ETC algorithm.

4. Conclusion

In this work, the concept of optimizing the parameter settings of the ETC algorithm for the MovieLens 1M dataset was proposed. This study has substantially contributed to the improvement of recommendation systems by proposing a methodology that adjusts the ETC’s critical parameters within the context of the MovieLens 1M dataset, thereby enhancing the algorithm’s genre recommendation performance. A comprehensive series of experiments were undertaken to assess the efficacy of the proposed approach. The empirical findings suggest that the ETC algorithm, when applied to the MovieLens 1M dataset, with a horizon of 50,000 and an exploration length of 500 yields superior performance in recommending genres with the highest average ratings. The elucidation of this discovery serves to corroborate the effectiveness of the ETC algorithm within the specific context under investigation, thereby underscoring the prospective viability of this methodology within the broader purview of recommendation systems. Subsequent avenues of inquiry should encompass an extensive calibration of hyperparameters for the ETC algorithm across heterogeneous datasets, while concurrently attending to additional dimensions such as user predilections and film popularity. Such multifaceted considerations hold promise for fostering a recommendation system characterized by heightened robustness and personalized efficacy.