1. Introduction

Pacman, a classic game launched by Namco in 1980 [1], masterfully combines simplicity and complexity with its single, static maze and four algorithmically driven ghosts. If Pacman encounters a ghost, he loses a life and the game resets, unless he has consumed a "power pill" [2,3]. The maze's configuration shapes the gameplay and strategy, emphasizing procedural generation's importance in enhancing game variability and replayability [4]. This study employs dynamic maze generation to refresh Pacman, marrying nostalgic gaming with modern algorithmic design [5]. This research centers on innovative maze generation algorithms, with a particular emphasis on the improved Sidewinder approach. The initial phase involves the examination of five traditional algorithms - Binary Search Tree (BST), Sidewinder, Aldous-Broder, Wilson, and Recursive Backtracker. These traditional algorithms are used as counterexamples to showcase their inability to generate Pacman mazes effectively, given their design for ordinary maze scenarios unrelated to Pacman's unique gameplay. Subsequently, we delve into the realm of innovative algorithms, focusing on the improved Sidewinder, to explore its potential in generating engaging and challenging mazes for a custom Pacman version implemented using the Pygame library. Each algorithm, including the improved Sidewinder, undergoes rigorous testing and analysis. The generated mazes are meticulously evaluated based on complexity, challenge level, dead-end frequency, and overall gameplay experience. Through this comprehensive assessment, we aim to identify the most promising algorithm and optimize it for integration with the game's mechanics, elevating the dynamics of Pacman mazes.

2. Literature Review

In 2016, Safak, Aykut, Bostanci, Gazi Erkan, and Soylucicek, Ali conducted a study using genetic algorithms to auto-generate diverse mazes in Ms. Pacman, with the aim of enhancing replayability. Their focus on environmental design, rather than character intelligence, extended the game's lifespan. Their application illustrates the potential of heuristic methods in creating dynamic and solvable mazes, thus serving as a crucial reference for this study [6]. In Karlsson's text, the growing importance of Procedural Content Generation (PCG) in game development is discussed, particularly as it helps address rising production costs and player expectations. The role of PCG in creating game elements like mazes, which hold integral significance in games such as Pacman and roguelikes like Spelunky, is highlighted. Mazes not only structure game levels but also present challenges to players. The insights from Karlsson's exploration of PCG's role in maze generation, alongside evaluations of various maze-generating algorithms, offer valuable guidance to developers seeking to create diverse, engaging, and cost-efficient game content [7]. The principal aim of this research is to understand the applicability and effectiveness of different maze generation algorithms when implemented in Pac-Man. The selected algorithms for this study are Aldous-Broder, Wilson, Binary Tree, and Sidewinder. These algorithms were chosen due to their distinctive features and varied levels of complexity, which provide a broad overview of the possibilities in maze generation for gaming.

3. Selection of Algorithms

3.1. Mean Idea

Algorithms mentioned above at different stages of our research in order to achieve the best possible game experience and efficiency. Aldous-Broder and Wilson's algorithms are examples of 'random walk' algorithms that can generate perfect mazes with higher complexity and unpredictability [8]. In the initial stage of the experiment, we tried to perform the maze generation using an algorithm that fused Aldous-Broder and Wilson’s algorithm to obtain a high-quality complex maze while greatly improving the running speed. However, the complexity of the perfect maze greatly reduces the player's own maneuvering possibilities, and they will always have to follow the same path to get to where they need to be, which means that they will most likely pass the path of the ghosts, and there is no way to avoid them. At the same time, figure 1 shows that the resulting mazes often have long, narrow paths, and a single solution can cause irritation and aesthetic fatigue for the player.

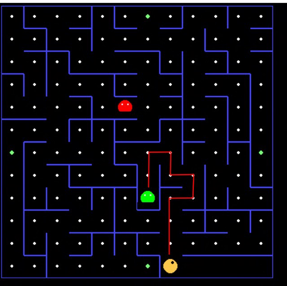
Figure 1. The figure shows that it is inevitable to meet the ghost if the Pacman want to eat.

Therefore, using algorithms with simpler logic is advantageous because they exhibit predictable generation patterns. This predictability enables easy integration of intervention conditions into the algorithm. Consequently, the randomly generated maze can be steered in the desired direction more effectively. In the following experiment, Sidewinder and Binary Tree algorithms are chosen as the main research objects due to their simpler generation logic, ease of monitoring, and high generation speed. These characteristics also contribute to improved code running efficiency. The aim of studying their similarities and differences is to identify the more suitable algorithm for Pacman and make necessary enhancements.

In the middle study, the focus is on the Binary Tree algorithm, which is considered one of the most straightforward maze generation algorithms. As the name suggests, this algorithm operates by making decisions between two available options at each step of the process [9]. Its core idea involves randomly selecting one of the two directions—east or south—and consistently carving paths from the northwest to the southeast.

Setting aside the two large paths at the top and far right showed in Figure 2, it's crucial to acknowledge the random nature of the Binary Tree algorithm, which causes the maze branches to continuously widen at random along a diagonal line. This behavior contrasts with the typical approach of dividing the grid using rows and columns, making it equally challenging to modify its performance.

Figure 2. A maze generated by Binary Tree algorithm.

Indeed, with the Binary Tree algorithm, there is no straightforward way to guarantee that it will develop in the desired direction by simply forcing paths to the east or south at specific steps. The algorithm's inherent randomness makes it difficult to achieve precise control over the maze's structure. For a Pacman maze, the typical preferences include simplicity, symmetry, multiple paths to specific areas, and it doesn't necessarily have to be a perfect maze.

3.2. Complexity

Table 1. Average complexity for each algorithm.

Table 1 shows the average complexity for each algorithm.

3.3. Dead ends

Table 2. Average number of dead ends for each algorithm.

Figure 3. Comparison of average complexity and average number of dead ends.

Table 2 shows the average number of dead ends for each algorithm, and figure 3 is the comparison of average complexity and average number of the dead ends for each algorithm.

3.4. Analysis

Since one of the criteria used to measure the complexity of the maze was based on the number of bends and the length of the path between two specified points [10], we applied an evaluation function based on the A-star algorithm. The algorithm includes a consistency heuristic function which can be represented as:

\( {h_{value}}=distance to the closest food+MST of the remaining foods \) (1)

In the evaluation function, we randomly generated six coordinates as the food of the current state. Then we let the Pacman agent find the shortest path to eat all the food. After the analysis of the running time, we can find that the Sidewinder algorithm reduces the running time compared to other traditional maze generation algorithms, which makes the game run more fluently. What’s more, the advanced data, complexity, and number of dead ends reveal that the Sidewinder is more suitable for the Pacman like game. The complexity test shows that other algorithms average complexity is about 70 -80. However, the Sindwinder is only about 50. It should be stressed out that the lower complexity does not means the game will be easier but means that the player will have more freedom in controlling the pac man. As a result, the game will be more fun and have more contents. It should also be noticed that the Sidewinder has much fewer dead ends than other algorithms. So, the player will have less chance to be blocked by the wall, thus being killed by the ghost. To make the game more fun, we always want the player to have the opportunity to avoid ghosts by anticipating their behavior, instead of just facing a wall and praying that the ghost will not come towards them. In conclusion, the Sidewinder should be the best choice for our research.

4. The Improved Sidewinder Algorithm

4.1. Why Sidewinder?

Sidewinder is a quick and simple algorithm, and it is modifiable since it is only partially randomized, unlike totally uncontrollable algorithms such as the Aldous-Broder algorithm and Wilson’s algorithm. Moreover, compared to the Binary Tree algorithm which has significant shortcomings, the Sidewinder algorithm’s defect is acceptable, and in fact, it could be modified as a characteristic of Pacman’s map - The connected grids in the first row of its maze are common. Another important feature of Sidewinder is that it generates mazes from bottom to top, this would be really useful since the Pacman maze is.

4.2. Improved Sidewinder for Pacman Mazes

However, the regular sidewinder is not perfect enough. It is based on a probability $p$ that demands the frequency of bars’ occurrence. Between every two bars, in which we call the set of all the cells a ‘run’, we randomly select a single cell and connect it with its neighbor above. As a result, the original problem still exists that a ghost can easily block the only way for the player to move upward. When there exists a ghost that moves toward the player, there is no chance for the player to win the game. In the normal Pacman game, most hallways have at least two exits.

The modified Pacman mazes generation algorithm has several differences.

1.A new parameter $e$ determines the portion of cells that connect to its top. For example, if $e$ is 3, then every three cells at average in a ‘run’ list would add a cell that will connect to its neighbor above.

2.The generated maze will be symmetric, so the algorithm only generates the bottom half of the algorithm. As it is generating, the upper half would copy the action of the bottom.

3.The algorithm creates a square in the middle where ghosts will spawn. In the maze with odd dimensions, the square is 3*3, while in the maze with even dimensions, its size will be 4.

4.Two symmetric rows will be selected by the algorithm (uniformly at random), of which the leftmost cell and the rightmost cell are connected (i.e., the Pacman and ghosts can move between the sides of those two rows like the original Pacman game.).

Figures 4 and 5 are examples of the Pacman map generated by the algorithm:

4.3. Advantages

4.3.1. Speed. The improved algorithm has a similar structure to the original Sidewinder algorithm. So, it is equally efficient as the previous one.

4.3.2. Flexibility. The two parameters of the algorithm could easily influence the difficulty and complexity of the maze when needed. Simultaneously, the algorithm itself is also easy to modify and elaborate more specific mazes.

4.3.3. Distinctiveness. Every single map is unique and has its own characteristic. The player will never feel bored with the Pacman game from now!

5. Conclusion

This paper mainly discusses different maze generation algorithms and their applications in Pacman games, including: introduces the traditional maze generation algorithms such as binary tree, Sidewinder, Aldous-Broder, etc., and analyzes the limitations of these algorithms in generating mazes for Pacman games. The Sidewinder algorithm was then compared and selected as the basis for the improvement, because the maze it generated was relatively simple, symmetrical, and had multiple solution paths, making it more suitable for Pacman games. Therefore, this paper proposes an improved Sidewinder algorithm, adding adjustable parameters to control maze complexity and the number of dead ends, so that the generated maze is more suitable for Pacman's game play. The improved Sidewinder algorithm has the advantages of fast generation speed, high flexibility and strong unique maze. Finally, the paper concludes that the improved Sidewinder algorithm is more suitable for generating dynamic and challenging mazes for Pacman games than the traditional algorithm, which can improve the game experience.

Acknowledgment

Kwan Man Cheng and Hongfan Liu contributed equally to this work and should be considered co-first authors.