1.Introduction

In recent years, the development of e-commerce has been rapid, with online retail sales exceeding 13 trillion yuan in 2022 [1]. Influenced by certain holidays, the order volume of e-commerce users experiences significant fluctuations, or unexpected events such as epidemics, earthquakes, etc., result in the temporary or permanent closure of logistics facilities. The current domestic logistics emergency dispatch system is not comprehensive enough, leading to severe economic losses. Therefore, establishing a sound emergency dispatch measure for e-commerce logistics has become a necessity of the times, and related decision optimization problems have become one of the hot topics in this research field.

To address the optimization problem of the logistics dispatch system, scholars both domestically and abroad have conducted extensive research. Regarding model construction and algorithms, Li Xiujuan [2] and others constructed a single-objective planning with the objective of minimizing the total time, employing an improved ant colony algorithm for solution. Guo Xiaoyu [3] treated changes in customer time windows as interference events in logistics distribution, considering customer satisfaction, path deviation, and cost deviation as three objectives. They built a multi-objective interference management model using dictionary sorting, combining ant colony algorithm and simulated annealing algorithm for solution. Saibo Liu [4] and others proposed a multi-objective model for integrated scheduling of manufacturing and logistics services (DISML), optimizing delivery time and logistics costs. Qihao Liu [5] and others minimized the maximum completion time and energy consumption as objectives, constructing a model and using swarm intelligence algorithms to avoid the model falling into local optimal solutions. Zhiming Ding [6] and others considered the characteristics of information uncertainty in disaster relief processes, establishing an emergency material dispatch model with multiple emergency supply points and demand points based on gray interval numbers, and using a genetic algorithm for solution. In terms of path optimization, Geng Ruhua[7] and others, addressing the problem of inefficient scheduling, optimized the generated traffic logistics distribution through a real-time update principle for paths. He Yuxian [8], Dan Liu [9], and others established a system model with the minimization of the total planning path length as the objective, employing improved ant colony algorithm for optimization. Li Chaoqian [10] and others used simulated annealing algorithm to prevent local optimal solutions in path optimization.

The above-mentioned studies have achieved good application effects in addressing specific problems. However, they assume that all transportation sites are not damaged in the application scenarios, solving optimization problems with objectives such as minimizing total costs or minimizing total path lengths, i.e., mostly static problem-solving objectives. Obviously, emergency transport in the e-commerce logistics network involves dynamic planning, requiring the planning of optimal dispatch solutions when a specific site is shut down. This includes opening new paths or closing existing paths to minimize changes in the overall logistics system and maintain the highest stability. The goal is to quickly restore the original transportation capacity with minimal losses. To address this, a planning model and solution algorithm based on multi-objective dynamic decision-making are proposed, aiming to optimize and solve the emergency transport plan and structure of the e-commerce logistics network.

2.Multi-Objective Optimization Model

2.1.Problem Description

The e-commerce logistics network is a complex system composed of multiple logistics facilities (such as pickup warehouses, sorting centers, business branches, etc.) and the transportation routes between them. Its operational efficiency and costs are influenced by various factors. Many unexpected factors can lead to the temporary or permanent closure of sites, affecting the stability and reliability of the logistics network. Therefore, to improve the operational efficiency and reduce operating costs of the logistics network, it is necessary to predict the cargo volume at various logistics facilities and routes within the logistics network. Based on these predictions, rational transportation and sorting plans can be formulated. Additionally, when facing situations where sites are temporarily closed due to unforeseen events, it is crucial to design effective logistics network adjustment plans. This aims to minimize the negative impact of site closures on the logistics network, ensuring its normal operation. From this perspective, it can be considered as a cargo transportation and allocation problem after time series forecasting. Against this backdrop and considering practical requirements, a multi-objective optimization mathematical model is designed and established to address the cargo transportation scheduling problem under emergency conditions, taking into account multiple optimization aspects.

Figure 1 illustrates a schematic diagram of the cargo transportation model, including supply points: dispatching goods, transfer points: transferring goods, and receiving points: receiving goods.

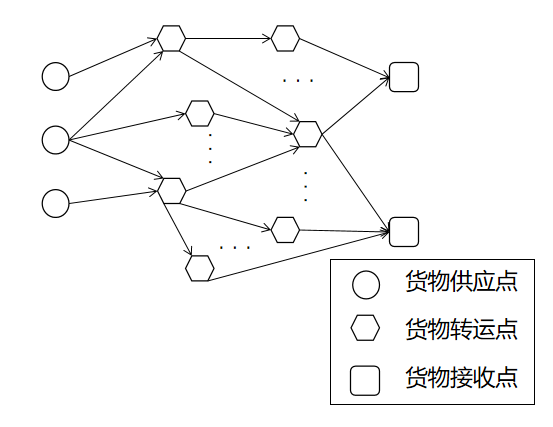
Figure 1. Schematic Diagram of Cargo Transportation

2.2.Model Construction

The overall objective is to minimize the number of routes with changes in cargo volume after a certain site closure and minimize the cumulative total of parcels that cannot circulate normally. In addition to this, the aim is to ensure that all parcels circulate as normally as possible while maintaining a balanced workload across all routes. This objective is transformed into three target functions.

Objective Function 1: Minimize the number of routes with minimal changes in cargo volume. To reduce the number of routes with cargo changes, the total number of routes opened and closed needs to be minimized. The formula for the total change in routes is as follows:

Objective Function 2: Minimize the load imbalance of each route. The balance of the load can be measured using the standard deviation. The formula is as follows:

\( \sqrt[]{\frac{\sum _{j∈V}\sum _{i∈V}({w_{ij}}-\overline{w}{)^{2}}}{n}} \)(2)

Objective Function 3: Minimize the cumulative total of parcels that cannot circulate normally. The formula is as follows:

\( \sum _{j∈V}\sum _{i∈V}{m_{ij}}(t) \)(3)

Considering the complexity of the cargo transportation process and addressing multiple optimization aspects, a multi-objective optimization model is established:

\( s.t. \left\lbrace \begin{array}{c} \sum _{i∈V}{x_{ijt-}}\sum _{i∈V}{x_{jit}}=(1-{p_{ijt}})\sum _{i∈V}{x_{ij(t-1)}}+(1-{q_{ijt}})\sum _{i∈V}{x_{ji(t-1)}},∀i,j∈V(5) \\ \sum _{i∈V}{q_{ijt}}*{x_{ijt}}=0,∀i,j∈V (6) \\ {x_{ijt}}≤{p_{ijt}}*{c_{ij}},∀i,j∈V (7) \\ {x_{ij}}(t)≤{x_{ij}}(0),∀i,j∈V,t=1,2,L,T (8) \\ \underset{i=1,2,L,n}{max}(x_{ij}^{last}-\frac{\sum _{i=1}^{n}\sum _{j=1}^{n}x_{ij}^{last}}{n})-\underset{i=1,2,L,n}{min}(x_{ij}^{last}-\frac{\sum _{i=1}^{n}\sum _{j=1}^{n}x_{ij}^{last}}{n})≤σ (9) \\ {x_{ijt}}∈Z (10) \end{array} \right\rbrace \)

In the model, Equation (4) represents the optimization objective; Equation (5) states that the total incoming cargo equals the total outgoing cargo plus the incoming cargo at new points minus the outgoing cargo at new points; Equation (6) ensures that the flow of goods from a closed node is zero; Equation (7) restricts the transportation capacity of newly opened routes to not exceed the maximum capacity of existing routes; Equation (8) ensures that the cargo quantity on each route in each time period does not exceed the initial value; Equation (9) aims for a balance in the quantity of goods on all routes; and Equation (10) ensures that the quantity of goods on each route in each time period is a non-negative integer.

2.3.Model Parameters and Variables

Table 1. Definition of Model Variables and Parameters

3.Solution Algorithm for the Model

LSTM (Long short-term memory) [11] is a special type of recurrent neural network that addresses the issues of vanishing gradients and exploding gradients during the training process of long sequences. It possesses the capability of maintaining long-term memory. In this model, its role is to predict future cargo quantities. Simulated Annealing Algorithm is a probability-based algorithm derived from the principles of solid annealing. The algorithm's concept is to start from a higher initial temperature, gradually decrease the temperature until it meets the conditions of thermal equilibrium. At each temperature, conduct n rounds of searching. During each round, add random perturbations to the old solution to generate a new solution. The new solution is accepted according to certain rules. Its advantage lies in its ability to search for the optimal solution within a large-scale search space and to some extent avoid falling into local optimal solutions. This algorithm is used to find the optimal solution for the model.

3.1.LSTM Model Algorithm

Initially, LSTM is used to predict the logistics quantity between various sites for a certain period in the future. The internal structure of LSTM is illustrated in Figure 2.

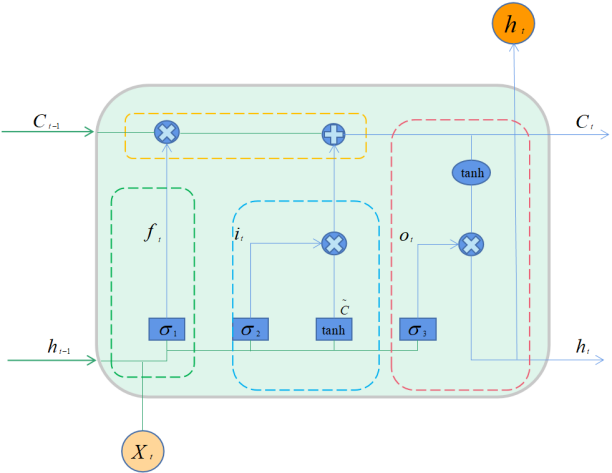
Figure 2. Internal Structure of LSTM Unit

In the figure: h is the hidden state, representing short-term memory. C is the cell state, representing long-term memory.\( {σ_{1}} \)is the forget gate.\( {σ_{2}} \)and tanh form an input gate.\( {σ_{3}} \)is the output gate.

3.2.Simulated Annealing Algorithm

Based on the data predicted by LSTM, randomly damage one site, construct a multi-objective optimization problem, and use the simulated annealing algorithm for solution.

The simulated annealing algorithm ^[12-13] can be roughly divided into two cycles: Cycle One involves iterative generation of new solutions. At any temperature reduction, a new solution is generated through random perturbation. The change in the objective function value is calculated to determine acceptance. Cycle Two, the slow temperature reduction, repeats the iterative process. After completing iterations at a fixed temperature, the temperature is slowly lowered, allowing the algorithm to possibly converge to the global optimal solution.

Parameter Selection:

(1) Choice of control parameter\( {T_{i}} \)and initial value\( {T_{0}} \).

\( {T_{i}} \)represents the quantity of added cargo, where each control parameter\( {T_{i}} \)corresponds to a solution\( {x_{i}} \). Based on preliminary analysis of the global optimal solution and search range, considering the scale of the problem, the initial value\( {T_{0}} \)is chosen as 200.

(2) Decay function for control parameter\( {R_{i}} \):

Due to the specific nature of the problem, a special decay function is constructed to perform "cooling" on the program:

\( \begin{cases} \begin{array}{c} {T_{i+1}}={T_{i}}-1 ({T_{i}}≥1) \\ {T_{i+1}}={T_{i}}-0.1 ({T_{i}} \lt 1) \end{array} \end{cases} \)(11)

Commonly used decay functions are\( {T_{i+1}}={αT_{i}},i=0,1,2,… \), where\( α \)can take values from 0.5 to 0.99.

(3) Markov Chain Length:

The selection of the Markov chain length should ensure reaching a quasi-equilibrium state at each value of the control parameter. For simple cases, it can be directly set as:

\( {L_{i}}=100n \)(12)

Here,\( n \)is the problem size, and in this case

(4) Acceptance Function:

\( p(i⇒j)\lbrace \begin{array}{c} 1 if f(i)≤f(j) \\ exp{(}\frac{f(i)-f(j)}{k{L_{i}}}) else \end{array} \rbrace \)(13)

In situations with a large,\( {L_{i}} \)at high temperatures, the denominator is large, and since this is a negative exponent, the acceptance probability is close to one. This means that a new solution\( {x_{j}} \)that is worse than the current solution\( {x_{i}} \)might be accepted, providing the possibility of escaping local optima.

(5) Stopping Condition:

\( {L_{i}}={L_{f}}=0.1 \)(14)

At high temperatures, a broad search has been conducted, identifying regions where the best solution may exist. At low temperatures, a sufficient local search is performed, increasing the likelihood of finding the global optimum. Hence,\( {L_{f}} \)is set to a sufficiently small number.

Finally, the values for the cooling schedule are shown in Table 2:

Table 2. Cooling Schedule

4.Experimental Results and Analysis

After the completion of model construction and algorithm determination, simulation experiments were conducted to simulate the e-commerce logistics emergency dispatch system. The following case uses the Matlab R2022a environment for simulation experiments. Simulations were carried out under the existing logistics scheduling system, where certain sites or some sites were suddenly shut down due to overload, natural disasters, or other special reasons. The model and algorithm were employed to timely adjust logistics, ensuring a balanced workload across all routes as much as possible. Goods were distributed to sites with larger processing capacities or to sites originally related to the shut-down sites, avoiding logistics stagnation caused by unforeseen circumstances.

77 sites were randomly generated, including 58 sites for both sending and receiving, 14 sites for sending only, and 5 sites for receiving only. Seasonal cargo transfer volumes between two sites were generated for two years. The directed graph visualizing the flow of goods between all nodes is shown in Figure 3:

Figure 3. Directed Graph of Full Node Flow

LSTM was used to predict the future cargo flow for the next month. If a site was shut down, the site was temporarily removed, and the model and algorithm were used to find a solution. Here, assuming that the DC9 site was temporarily shut down for a special reason, DC9 was removed for experimental verification. The newly added routes after removing DC9 are shown in Table 3:

Table 3. Data for Newly Added Routes after Removing DC9

From the table, it can be observed that the newly added route is DC3-DC1. DC1 was previously only connected to DC9, and after removing DC9, DC3 was added as a transfer station. The average flow for the new route in January is 906, far less than the maximum carrying capacity of the network, showing a significant improvement.

A comprehensive analysis of the data was conducted, calculating the average cargo value, maximum load, workload ratio, and remaining capacity for each route. The top five results are displayed in Table 4.

Table 4. Workload Table for Sites

From Table 4, it can be concluded that the workload ratio for routes 69→5, 69→14, 69→62 is 100%, while the workload ratios for other routes do not reach 100%. This indicates that the deletion of DC9 and the addition of the 3→1 route have no impact on the overall distribution results. There are no overloaded routes, meeting practical requirements.

5.Conclusion

In the context of emergency parcel dispatch and structural optimization in e-commerce logistics networks, a planning model and solution algorithm based on multi-objective dynamic decision-making for circulation were established. The model utilizes Long Short-Term Memory (LSTM) to predict transportation demands over a future period and dynamically adjusts routes and loads based on the opening or closing of logistics sites. The model aims to minimize the number of routes with changes in cargo volume, minimize the load imbalance across routes, and minimize the cumulative total of parcels that cannot flow normally. The simulated annealing algorithm was employed for solving, resulting in a circulation plan that meets the requirements. Finally, the optimization of the overall logistics network was achieved by adding new sites and routes. The main conclusions are as follows:

1: In the practical context of emergency parcel dispatch and structural optimization in e-commerce logistics networks, a planning model based on multi-objective dynamic decision-making for circulation is proposed. This model effectively addresses the issues related to emergency parcel dispatch and structural optimization in e-commerce logistics networks.

2: The use of LSTM to predict transportation demands over a future period enhances the accuracy and adaptability of the model. The application of the simulated annealing algorithm ensures the efficiency and quality of the model's solution.

3: Through simulation experiments, the effectiveness and practicality of the model were verified. Focusing on how to maintain the stability of the existing logistics network in emergency situations and promptly restore the normal operation of the network in terms of cargo dispatch, the model addresses challenges and potential cost savings in transportation. It provides a new approach and method for the management and optimization of e-commerce logistics networks.