1. Introduction

In the field of multi-armed bandit, considerable research has been conducted to explore different algorithms and approaches. ε-greedy, ETC, UCB, and Thompson sampling are among the commonly studied algorithms [1]. These algorithms aim to balance the exploration and exploitation trade-off to maximize the cumulative reward. Meanwhile, there are various variants of the multi-armed bandit problem and corresponding algorithmic improvements being proposed, such as the study of the multi-armed bandit considering multiple objectives, with limited weapon lifetimes or bandit algorithms incorporating contextual information. However, there have not been many articles that provide a comprehensive summary and comparison of their improvements in various application areas.

Therefore, the main objective of this study is to provide a comprehensive survey of the application and technical improvement of the multi-armed bandit model. Therefore, the main purpose of this study is to provide a comprehensive survey of the application and technological improvement of the multi-armed bandit model, including in recommendation systems, healthcare, how the MAB is specifically used for modeling, and what kind of adjustments can be made to the model to satisfy the different characteristics of the real-life applications of the various fields.

A systematic review and analysis of existing literature will be made to answer the questions above. Relevant studies, articles, and papers are reviewed to gather information on current algorithms and their applications.

The significance of this article is reflected in the following points. Firstly, this article can provide a comprehensive survey of the current research progress. It helps researchers learn more quickly about the main applications in the field of multi-armed bandit and the corresponding improvements in algorithms and models. By summarizing practical application scenarios, this article can highlight the potential value of multi-armed bandit algorithms in real-world applications; by presenting improved and variant models, the article can reveal research challenges in the field of multi-armed bandit. Finally, this article can provide insights for the future development of multi-armed bandit algorithms and their applications. The following sections will introduce the different aspects of multi-armed bandit, including its applications, improved algorithms, and discussions of the findings.

2. Multi-armed bandit problem overview

The multi-armed bandit machine problem originates from casino slot machines in which the player has to choose among multiple arms (draws) with different probabilities of rewards on each arm. In the multi-arm bandit machine problem, the main goal is usually to find a strategy to minimize the cumulative loss or maximize the cumulative reward. In real life, people are faced with many situations where they need to make decisions to maximize rewards, such as choosing the most effective way to advertise, choosing the best treatment when treating patients, and so on. These decision-making problems can be modeled as multi-armed bandit problems. Specifically, different choices are often seen as different “arms”, and the effect of choosing a particular arm is modeled as the “reward”. A simple abstraction of the scene is shown: First, given a time step t = 1, 2, ..., T. Second, in round t, the user chooses arm i and receives a randomized reward feedback \( {r_{i,t}} \) , where \( {r_{i,t}} \) obeys a static distribution. Third, each time the user can only observe the payoffs of the chosen arm i, and the payoffs of the other arms are not observed. The overall goal is to maximize the total payoff in round T, which can be expressed as \( \sum _{τ=1}^{T}{r_{τ}} \) . The following are a few mainstream algorithms for the original multi-arm bandit machine problem.

ϵ-greedy is probably the most widely used strategy to solve the bandit problem and was first described by Watkins [2]. In the ϵ-greedy strategy, exploration is performed with a probability of ϵ, which means some arms are chosen at a random frequency of ϵ [3]; the rest of the time, the arm with the largest average reward so far is chosen.

2.1. The Explore-Then-Commit (ETC) Algorithm

The simplest variant of ϵ-greedy's strategy is the ETC strategy [3]. The ETC algorithm is the intuitive approach of exploring before exploiting. It divides the whole process into two non-intersecting phases, exploration and exploitation. In the exploration phase, this paper explores all the arms m times; in the exploitation phase, based on the previous exploration of K arms, we subsequently select the arm with the highest average reward.

Algorithm ETC(m)

Input K and m

Exploration phase:

foreach t = 1, 2, . . . , mK do

For each arm \( {a_{i}} \) , randomly explore m times

end

Count the average gain of each arm ai in the first mK rounds, which is \( \hat{μ}({a_{i}}) \)

Choose the one with the largest average gain among the K arms, which is \( a=\underset{i=1,…,k}{max}\hat{μ}({a_{i}}) \)

Exploitation phase:

foreach t = mK+1, mK+2, . . . , T do

Always choose the most profitable of the preceding mK rounds, which is \( a=\underset{i=1,…,k}{max}\hat{μ}({a_{i}}) \)

end

Figure 1 shows the expected regret for ETC on a Gaussian bandit with different means. It can be clearly seen that the choice of m is important in the ETC algorithm, if m is too small, mistakes are likely to be made when searching for the arm with the higher reward, but if m is too large, a lot of opportunities for exploitation will be sacrificed. This also suggests the dilemma of exploration and exploitation. Fortunately, however, the ideal m can be derived from the formula of regret values.

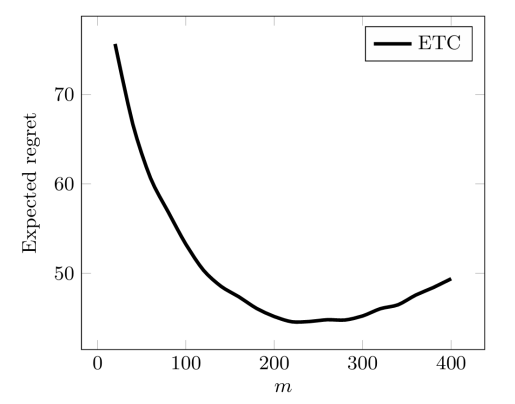
Figure 1. Expected regret for ETC over 105 trials on a Gaussian bandit with means µ1 =0,µ2 = −1/10 [4]

2.2. The Upper Confidence Bound Algorithm

The core idea of the UCB algorithm is optimism in the face of uncertainty, exploring with the most optimistic attitude given the current information. The algorithm maintains an upper confidence bound for each arm, which is usually higher than the actual expectation. Arms with a high current success rate are highly utilized, and arms with high uncertainty are highly explored as well. The easiest way to rate a arm is to take it as the sum of two values. That is: the upper confidence bound = estimated reward probability + exploration bonus [5]. Where the exploration bonus decreases as the number of times this arm is selected increases. The algorithm will choose the arm with the highest upper confidence bound every time.

Algorithm UCB(δ)

Input K and δ

foreach t = 1, 2, . . . ,T do

Choose action A_t = argmax_i UCB_i(t − 1, δ)

Observe reward X_t and update upper confidence bounds

end

The results in Figure 2 show a generalization. If ETC chooses the optimal m, it slightly outperforms UCB without parameters. However, in most cases, ETC usually does not outperform UCB.

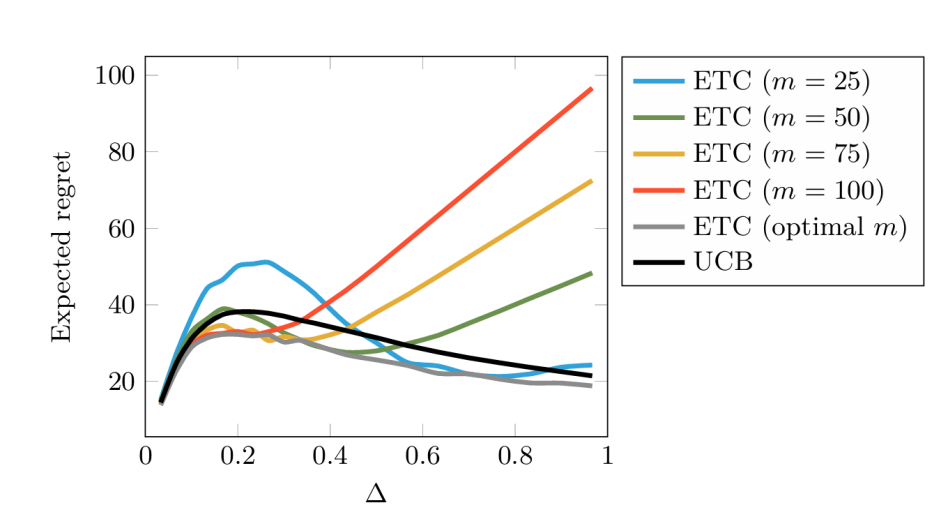
Figure 2. Experiment showing universality of UCB relative to fixed instances of ETC[4]

2.3. Thompson sampling

Thompson sampling utilizes a priori knowledge to a greater extent than UCB. In multi-armed bandit machines, the Bernoulli distribution happens to have the Beta distribution as the conjugate prior. To be precise, in the multi-armed bandit machine problem, after each selection of the recommended project, the parameters of the Beta distribution are updated based on whether there is revenue. As the number of selections increases, the parameters of the Beta distribution are constantly updated, and the transformed rate of the multi-armed bandit machine can be estimated more accurately.

Algorithm Thompson Sampling for Bernoulli bandits

For each arm i = 1, . . . , T set S_i = 0, F_i = 0.

foreach t = 1, 2, . . . , do

For each arm i = 1, . . . , N, sample θ_i(t) from the Beta(S_i + 1, F_i + 1) distribution.

Play arm i(t) := arg maxi θi(t) and observe reward rt .

If r = 1, then Si(t) = S_i(t) + 1, else F_i(t) = F_i(t) + 1.

end

3. Real-life applications of bandit

Multi-armed bandit machine models are widely used in fields such as recommender systems, healthcare, telecommunications and finance [6]. With the flexible application of the model, it also provides a lot of support for the development of these fields.

3.1. Recommender systems

Multi-armed bandit machine models are widely used in recommendation systems to select products that users like and are more likely to click on. Different products are treated as different arms, and the recommendation system can quickly adjust the recommendation strategy based on user feedback. For example, Amazon's product recommendation system uses a multi-arm bandit machine model to personalize recommendations to users and increase their purchase rate.

3.2. Healthcare

In healthcare, multi-armed bandit machine models can be used to make optimal treatment decisions. In clinical medicine, different treatments are often seen as different arms, and the effect of the treatment is the "reward". In this way, the best treatment plan can be selected based on the patient's situation and feedback, reducing trial and error. For example, in cancer treatment, a multi-arm bandit machine model can assist doctors in selecting the most effective chemotherapy drug combination regimen.

3.3. Finance

In finance, multi-arm bandit machine models can be used for investment and risk management. In this case, different portfolios are treated as different arms. By dynamically adjusting portfolios, multi-armed bandit machine models can increase investment returns and reduce risks. For example, fund management companies can use multi-arm bandit machine models to optimize portfolio allocation for more stable returns and risk management.

4. Improved bandit

4.1. Multi-objective Multi-armed Bandits

Many problems in the real world are essentially multi-objective environments with conflicting goals. However, the classical multi-armed bandit machine model obtains a single measure of reward for each choice. In response to this dilemma, the paper Designing multi-objective multi-armed bandits algorithms [7] proposes an algorithmic framework for Multi-Objective Multi-Arm Bandits (MOMABs) with multiple rewards, in which each arm is associated with a fixed equal-range randomized reward vector, and only one arm is played at a time. It considers multi-objective (or multi-dimensional) rewards and introduces multi-objective optimization techniques to multi-arm bandit algorithms.

The framework allows considering different partial order relationships in multi-objective optimization. A common approach is to use scalarization functions that combine multiple objectives into a single one. The scalarization technique makes it straightforward to apply in current multi-armed bandit machine frameworks, but the efficiency of the algorithm depends strongly on its type (linear or nonlinear, e.g., Chebyshev function) and parameter selection. Another approach is to use Pareto search for multi-objective optimization. The use of Pareto dominance relations allows direct exploration of the multi-objective environment, but this can lead to a large number of Pareto-optimal solutions.

The article just mentioned [7] also proposes and uses three regret metrics to evaluate the performance of MOMABs. They extend the standard UCB1 algorithm to a scalarized multi-objective UCB1 algorithm and introduce a Pareto UCB1 algorithm. Both algorithms achieve a recognized logarithmic upper bound on the expected regret value. It was found that the Pareto UCB1 had the best empirical performance.

4.2. Mortal Multi-Armed Bandits

An important application of multi-armed bandit models in the economy is online advertising, where the ad provider gets paid when the ad is clicked. So it is important to select from a large number of advertisements those that are more likely to be clicked on to maximize revenue. In this case, each ad can be viewed as an arm, which may or may not be clicked on by the user (providing a reward), so any multi-armed bandit strategy can be used in the ad selection problem.

However, a standard assumption in a multi-armed bandit environment is that each arm exists permanently. Once the optimal arm is essentially determined, the number of times it is used for exploration decreases. However, in real-world applications such as online advertising, for example, mentioned in Mortal multi-armed bandits [8], advertisements are regularly generated and disappear from the marketplace, with a limited lifespan due to the nature of the advertisement's content and the advertisement's budget, etc.; and the number of available advertisements tends to be very large, which leads to the fact that if the standard multi-armed bandit machine model were used, since the time required is proportional to the number of bandit machines, the convergence of the standard strategy will be slow.

So algorithm needs to choose among a large collection of ads, but in general, there is no way to confirm with certainty the level of reward for an ad during its life cycle. Chakrabarti, D., Kumar, R.'s-article [8] proposes an optimal algorithm for the state-aware (deterministic reward function) case, and based on this technique an algorithm for the state-oblivious (stochastic reward function) case is obtained, and validated the algorithm on various payoff distributions. In the standard multi-armed bandit problem, the deviation of the algorithm from the optimal total payoff is only O(ln t) [9], whereas in the mortal multi-armed bandit problem, the deviation of the algorithm from the optimal total payoff may reach Ω(t).

A generalized heuristic for modifying the standard multi-armed bandit algorithm to make it more suitable for the mortal arm environment is also provided. That is an ephemeral-based heuristic: at the beginning of each ephemeral, a subset of k/c arms is selected from a total of k arms in a uniformly randomized manner; the standard bandit algorithm is then run on these arms until the end of the ephemeral, and then repeated. In short, the burden on the bandit algorithm is reduced by the operation of selecting a subset, which reduces the number of explorations and speeds up convergence in exchange for finding a potentially optimal arm in the k/c subset.

4.3. Contextual multi-armed bandits

In the classic bandit machine model, the reward for each selection of an arm comes from a fixed distribution of rewards. Internet search engines, such as Google, Yahoo!, and Microsoft’s Bing, receive rewards from advertisements shown to a user’s query [10]. However, such a definition is a bit rigid in real-life applications. In online advertising applications, the distribution of rewards for an arm can be different when the user's age or geographic location is different, or when other page information such as the page topic is different. Apart from that, in a clinical trial with two drugs, people's genetic or demographic information can be characterized to influence the effectiveness of the medication [11]. Such different features can be summarized as "contexts", and this information can affect the arm's reward distribution. Therefore, the decision maker needs to select an arm based on this contextual information.

The agent observes an N-dimensional context or feature vector before choosing an action. This context and experience together determine which arm to select in the current round. As more rounds are selected, the agent can increasingly learn the relationship between the contextual feature vector and the reward and make better predictions with the current context.

4.4. Combinatorial multi-armed bandits

In the problem of advertisement placement, an advertiser may place a set of web pages (assuming he can select up to K pages) on a website instead of a single advertisement. What the advertiser hopes to do is to maximize revenue by constantly experimenting with selecting certain k ads and obtaining the click-through rate to place the set of ads that the user prefers.

Unlike traditional multi-armed bandit machine algorithms, in this case, k ads are going to be selected at the same time each time, rather than placing the ads individually. Instead, the arms are combined to be selected together. In addition, the reward gained in this way cannot be measured as a simple linear function of the arm's reward. In the online AD example above, the collective reward for these "arms" is 1 if the user clicks on an AD on at least one of the pages, and 0 if not.

A simple idea would be to consider each possible combination as an arm so that the classic multi-armed bandit machine framework could be applied. Unfortunately, such an operation would lead to a catastrophic "combinatorial explosion" in the number of arms. In addition to this, it is not possible to observe any information about the underlying arm results. A corresponding framework for combinatorial multi-arm bandit (CAMB) machines is presented in Combinatorial multi-armed bandit: General framework and applications [12], which accommodates a large class of nonlinear reward functions among combinatorial and stochastic arms. In each round of the game, a superweapon is played, and the results of all the weapons in the superarm (and possibly some other triggered weapons) are revealed. The CMAB algorithm needs this information from past rounds to decide which superarm to play in the next round.

5. Conclusion

This paper provides an overview of applications and technical improvements to the multi-armed bandit machine problem. It first provides an overview of the multi-armed bandit machine problem, explains the general modeling approach to the problem, and summarizes several basic mainstream algorithms. This is followed by an introduction to its practical applications in mainstream application domains, such as recommender systems and the medical field.

The main part of the article summarizes several variants of multi-armed bandit machine frameworks and illustrates the corresponding application scenarios. For online advertisements with a limited lifecycle, it corresponds to the mortal multi-armed bandit machine; for clinical medications that consider patient characteristics, the contextual multi-armed bandit machine framework can be applied; and for advertisements that can be placed in a group at a time, the combined multi-armed bandit machine framework can be used.

Through this article's overview, scholars can more quickly understand the framework of classical multi-armed bandit machines, the different variants derived from them, and the corresponding characteristics in actual more complex problems. Perhaps it can also provide a little inspiration for future research in this field, such as combining variants of the multi-armed bandit machine framework corresponding to different problems to apply them to more complex problems; or these variants of the framework can be experimentally verified and their performances can be compared. Or multi-armed bandit can also be further combined with deep learning to train higher-performing models.