1. Introduction

Autonomous robots have become a hot topic and have received increasing attention and interest in different spheres with continuous research in these decades. Autonomous robots have been applied to various circumstances, such as floor-cleaning robots [1], [2], autonomous driving [3], and others. Autonomous robots have also been used for military missions, such as terrain exploration [4] for searching dangerous items, patrolling [5], and surveillance [6], [7]. Path planning has also been carried forward as the fundamental part of an autonomous robot. Researchers use various theories or algorithms to optimize the path planning algorithm, such as particle swarm optimization algorithm [8], heap-based optimizer [9], gravitational search algorithm [10], and plenty of other models and algorithms. This paper presents a path planning generator based on a chaos game optimization algorithm. Before introducing the chaos game optimization algorithm, this paper will introduce the chaos theory first.

A branch of mathematics is called chaos theory [11]. It deals with how dynamic systems that are susceptible to beginning conditions behave. It can manage intricate systems that are challenging to forecast, such as weather patterns, stock market fluctuations, and the behavior of living things. According to chaos theory, even little changes in the original circumstances can result in drastically different results, making it challenging to forecast long-term behavior. The underlying patterns and structures that arise from complex systems are the focus of chaos theory, despite its name, which implies disorder or unpredictability. Numerous natural phenomena have been better understood thanks to the study of chaos theory, which also has valuable applications in physics, engineering, and economics. Robot path planning can benefit from chaos theory to increase its randomness and unpredictability. Chaos theory, on the other hand, focuses on unpredictable complex systems. It doesn't necessarily follow that these systems are unmanageable or unbridled by restrictions. To find underlying patterns and structures in complex systems, chaos theory is frequently applied. Applications of chaos in robotics can be divided into two categories: chaos analysis and chaos synthesis [12]. To monitor and examine the unpredictable behavior of robots is chaos analysis. To enable the robots to carry out specific tasks, chaos is manually created through the process of chaos synthesis.

A metaheuristic algorithm is the chaos game optimization algorithm (CGO) [13]. It was created to address optimization issues. The chaos game approach is used to evaluate the fractal configuration and fractal self-similarity problems. The chaos game method is the foundation of the CGO algorithm. Chaos game theory serves as the foundation for the CGO algorithm, and game theory also serves as the basis for the algorithm's general representation. Fractals are produced mathematically using the chaotic game. Starting with a polygon shape, a random point is then chosen. The objective is to create a series of points iteratively that will lead to a sketch with comparable shapes at various scales. The polygon's vertices must be properly positioned to accomplish this. After this is complete, a random point is selected as the fractal's initial starting point. To identify each following point in the series, an arbitrary polygon vertex is chosen, and a fraction of the distance between that vertex and the preceding point is calculated. A fractal is produced by repeating this procedure with various random picks. Three vertices can be used to create a Sierpinski triangle with a factor of 1/2. It is possible to generate a Sierpinski Simplex with \( N-1 \) dimensions when the starting vertex count approaches \( N \) . The Sierpinski triangle's final shape and degree of self-similarity are depicted in Figure 1.

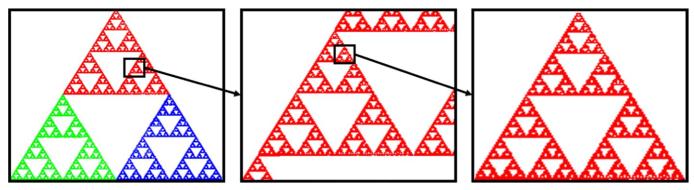
Figure 1. The final shape and self-similarity of the Sierpinski Triangle in different scales [13].

The paper presents a path planning generator that is based on the Chaos Game Optimization (CGO) algorithm. This algorithm uses chaos theory and the principle of the chaos game to create an efficient and robust solution for path planning in complex and dynamic environments. The paper explains the process of path planning using the CGO algorithm, including the initialization of candidate solutions and the iterative process of updating their positions and fitness values. MATLAB simulation results demonstrate that the CGO algorithm is effective in generating optimal paths. This paper introduces a new strategy for path planning using the CGO algorithm and provides examples through MATLAB simulations.

This paper is organized as follows: Section Ⅱ shows some related works of chaos game optimization algorithm (CGO), including the inspiration of the CGO algorithm and a few path planning generators using other methods. Section Ⅲ presents the procedure of path planning using the CGO algorithm and shows the simulation results in MATLAB. The conclusion of this path planning generator will be presented in Section Ⅳ, alongside the future challenges.

2. Related Work

This section presents the chaos theory and the inspiration of the chaos game optimization (CGO) algorithm. A few path planning generators using other methods are also shown.

2.1. Chaos Theory

An area of mathematics called chaos theory [14] examines how dynamic systems that are subject to starting circumstances behave. It deals with elaborate, seemingly random behavior displayed by complex systems. Chaos theory has recently found use in a number of industries, including robotics. The use of chaos theory in robotics research can improve the performance and capabilities of robotic systems by providing valuable insights into how they behave and are controlled [15].

According to the idea of chaos, even minor modifications to the starting circumstances can have a significant impact on how a system behaves over the long term. This idea, known as the "butterfly effect," postulates that even little changes in the initial configuration or input might cause significant divergence over time. Robot mobility and behavior in robotics can be significantly impacted by minor disturbances or uncertainties in the initial conditions.

One area where chaos theory has been applied in robotics is in the analysis and control of robot dynamics [12]. Traditional approaches to robot control assume linear and predictable behavior. However, robots often operate in complex, uncertain environments where unexpected disturbances occur. Chaos theory provides a framework to understand and model the nonlinear dynamics of robots, considering their sensitivity to initial conditions and external influences. By incorporating chaos theory into control algorithms, researchers can design more robust and adaptive control strategies that can handle uncertainties and disturbances effectively.

Moreover, chaos theory has also been employed in the design of robot locomotion and navigation strategies. Robots operating in unstructured and dynamic environments must exhibit agile and adaptive behavior. Chaos theory offers insights into generating complex and unpredictable motion patterns, enabling robots to navigate challenging terrains or avoid obstacles in real time. By leveraging chaotic dynamics, researchers have developed novel locomotion strategies that mimic the natural movements of animals or exploit the inherent instability to achieve agile and efficient motion.

Furthermore, chaos theory has implications for swarm robotics [16], where a group of robots collaboratively solves tasks. The study of collective behavior in swarm robotics often involves the analysis of emergent properties and self-organization. Chaos theory provides a framework for understanding how simple local interactions between robots can create complex global behaviors. By harnessing the principles of chaos theory, researchers can design swarm algorithms that exhibit robustness, adaptability, and scalability.

Chaos theory has emerged as a valuable tool in robotics. By embracing the inherent complexity and sensitivity to initial conditions, chaos theory enables researchers to develop more robust control strategies, design agile locomotion patterns, and understand emergent behaviors in swarm robotics. The application of chaos theory in robotics opens up exciting possibilities for advancing the capabilities of robotic systems and enhancing their performance in real-world scenarios.

2.2. Inspiration of Chaos Game Optimization Algorithm

Chaos game optimization (CGO) is a nature-inspired optimization algorithm based on the principles of fractal geometry and the chaos game. The inspiration behind CGO comes from the observation that many natural systems exhibit complex and chaotic behavior yet can self-organize and adapt to changing environments. This led Talatahari and Azizi to explore the potential of fractal geometry and the chaos game as a means of developing a new optimization algorithm.

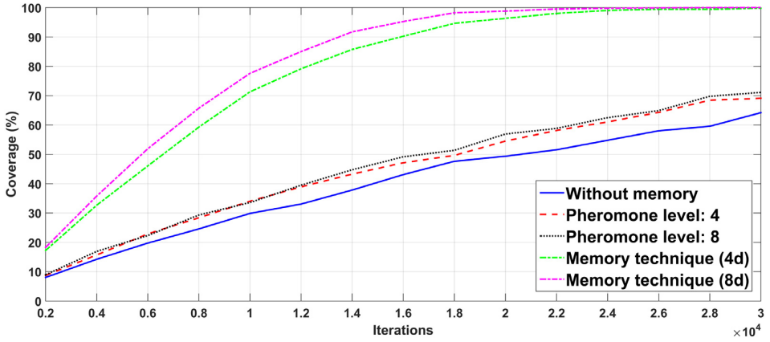
Figure 2. Coverage performance with respect to iterations, compared to motion in eight directions and pheromone [17].

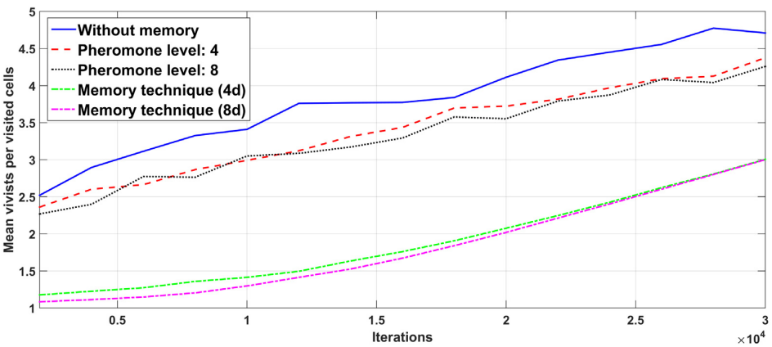
Figure 3. Mean visits for visited cells with respect to iterations, compared to motion in eight directions and pheromone [17].

The chaos game is a simple iterative algorithm that involves starting with a set of points within a geometric shape and randomly selecting one of these points as the current position. At each iteration, the current position is moved halfway towards a randomly chosen point from the original set. This process is repeated many times, resulting in a fractal pattern that resembles natural forms.

CGO extends the principles of the chaos game to optimization by using a similar iterative process to search for the optimal solution to a given problem. The algorithm starts with an initial population of candidate solutions and randomly selects one as the current position. At each iteration, the current position is moved towards a randomly chosen point that is closer to the optimal solution. This process is repeated many times, with the hope that it will converge to the global optimum.

One of the critical advantages of CGO is its ability to handle complex and non-linear optimization problems. Traditional optimization algorithms may struggle with such issues, as they often involve multiple local optima and non-convex objective functions. CGO's ability to explore the search space in a random and chaotic manner allows it to overcome these challenges and find better solutions.

CGO has been successfully applied in various fields, including engineering, finance, and computer science. Its ability to handle complex and non-linear problems makes it a powerful tool for researchers and practitioners alike.

2.3. Based on A Logistic Map and Modulo Tactics

The work [18] introduced a novel approach for chaotic path planning based on a modulo-based strategy and the logistic map. This method is quicker, more straightforward to use, and more effective overall because it does not require a Cryptographically Pseudorandom Bit Generator (CPRBG), unlike conventional methods. Numerous simulations revealed that the suggested strategy efficiently ensured path coverage as the number of iterations rose.

To enhance the technique further, the algorithm incorporated a pheromone-based memory, resulting in improved performance. Future studies will explore non-square grids with obstacles, generate paths using other chaotic maps and modulo strategies, apply the technique to fractional order systems, and address difficulties in multi-robot collaboration.

When dealing with multiple robots, additional considerations include sharing position information and preventing revisiting previous positions by allied robots. Other potential areas of exploration include introducing fictitious obstacles for increased unpredictability, adapting the approach for differential motion robots on continuous grids, implementing the method on mobile robots using microcontrollers, and exploring its application in encryption problems.

It is believed that this approach has significant potential for various chaos-related applications in robotics and engineering. The future research directions outlined aim to develop further and refine the practical utilization of this technique.

2.4. Enhanced by A Memory Technique

This study [18] introduces a new technique for chaotic path planning that incorporates a modified memory-based approach to enhance its performance. A pseudo-random bit generator is created using two straightforward chaotic maps, and it is then utilized to develop navigational instructions for an autonomous robot. While exploring an area, the robot moves randomly but often revisits previously explored cells. The suggested method addresses this problem by restricting the robot's chaotic motion to cells that have received the fewest visits, which improves performance in general.

The performance of this work is presented in Figure 2 and Figure 3.

2.5. Using Hybridized Regression-gravity Search Algorithm

The current study uses a hybrid approach to investigate how humanoid robots negotiate difficult terrain [19]. The path planning process is optimized by combining a classical linear regression-based technique with the gravitational search algorithm (GSA) and incorporating Chaos. This hybridization technique, known as RGSA, seeks to identify the optimum path while preventing rapid convergence and local traps. The performance of the RGSA model is improved by incorporating chaos. This modification enhances the model's ergodicity, randomness, and continuity, enabling more effective exploration and use of the search space. Investigations are made into the effectiveness of a number of chaotic maps, including the logistic map, the Gauss map, the piecewise linear chaotic map, and the sinusoidal map.

One or more humanoid robots (Nao robots) are used for the inquiry in both realistic lab settings and simulated situations. The robots navigate around both stationary and moving items in the search space. Webot software is utilized for simulation-based path planning, whereas the choreographer program is used for experimental path design. The differences between the modeling and experimental results are only 6% outside of acceptable ranges, indicating good agreement between the two sets of results.

The performance of the proposed controller is evaluated against vision-based and sensor-based methods in terms of operational expenses and trajectory smoothness. The research also looks into how mobile and humanoid robots can communicate with one another. The offered method can successfully avoid the mobile robot KHEPERA-II. In scenarios like soccer matches, where mobile robots might compete with Nao robots as players, this concept may be useful. The suggested methodology also has the advantage of lower operational costs, making it applicable to a wide range of industries, including multitasking, cooperative scheduling, and power distribution systems.

In this study, a brand-new method for path planning for humanoid robots on difficult terrain is presented. To find the best path, it is advantageous to combine linear regression with the gravitational search method and incorporate chaos. The experimental findings show that the suggested methodology is practicable and has potential applications in a number of fields.

3. Path Planning Using Chaos Game Optimization Algorithm and Simulation Result

This section shows the procedure of a path planning generator using the CGO algorithm and presents its simulation result in MATLAB R2023b.

3.1. Procedure of path planning using the CGO algorithm

3.1.1. Initialization. The initialization of the CGO algorithm is similar to other intelligent optimization algorithms. It randomly initialized in the scope of search space as follows:

x^j_i(0)=x^j_{i, min}+rand.(x^j_{i, max}–x^j_{i, min}),i = 1, 2,…, n, j=1,2, …,d (1)

where n is the number of candidate solutions in the search space, and d is the dimension of these solutions. x^j_i(0) represents the initial position of the solutions; rand is a random number in the interval of [0, 1]; x^j_{i, min} and x^j_{i, max} are the lower and upper limit for the jth decision variable of the ith solution candidate.

3.1.2. Update the position of the first three seeds. The mathematical description of updating the position of the first three seeds is as follows:

Seed_i¹ = X_i + α_i * (β_i * GB - γ_i * MG_i) (2)

Seed_i² = GB + α_i * (β_i * X_i - γ_i * MG_i) (3)

Seed_i³ = MG_i + α_i * (β_i * X_i - γ_i * GB) (4)

where X_i is the ith candidate solution; GB is the current best solution; MG_i is the mean values of some eligible seeds; α_i is a randomly generated matrix which simulates the motion position restrictions of the seeds; β_i and γ_i each represents a random integer with the value between 0 and 1, and they are possibilities of rolling a dice.

The three points of a Sierpinski triangle are X_i, GB and MG_i.

3.1.3. Update the position of the first three seeds. The mathematical description of updating the position of the fourth seed is a little different from the first three seeds, and it is as follows:

Seed_i⁴ = X_i (x_kⁱ = x_kⁱ + R), k = [1, 2, …, d] (5)

where k is a random integer within [1, d]; R is a random number within [0, 1] obeying uniform distribution.

In order to control and adjust the rate of exploration and development of the CGO algorithm, α_i can be determined according to formula (6) as follows:

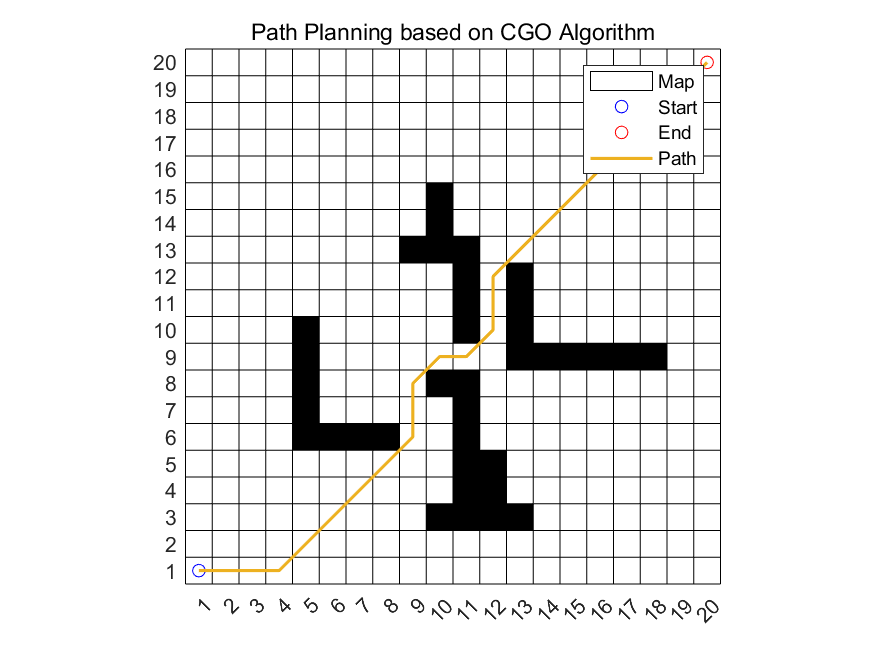
Figure 4. Path planning under four blocks.

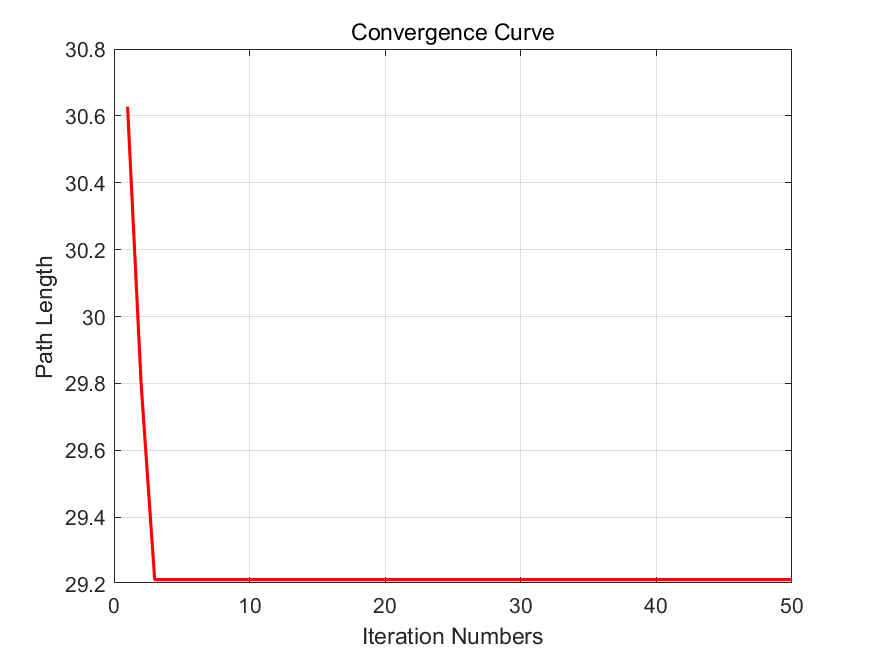
Figure 5. Convergence curve under four blocks.

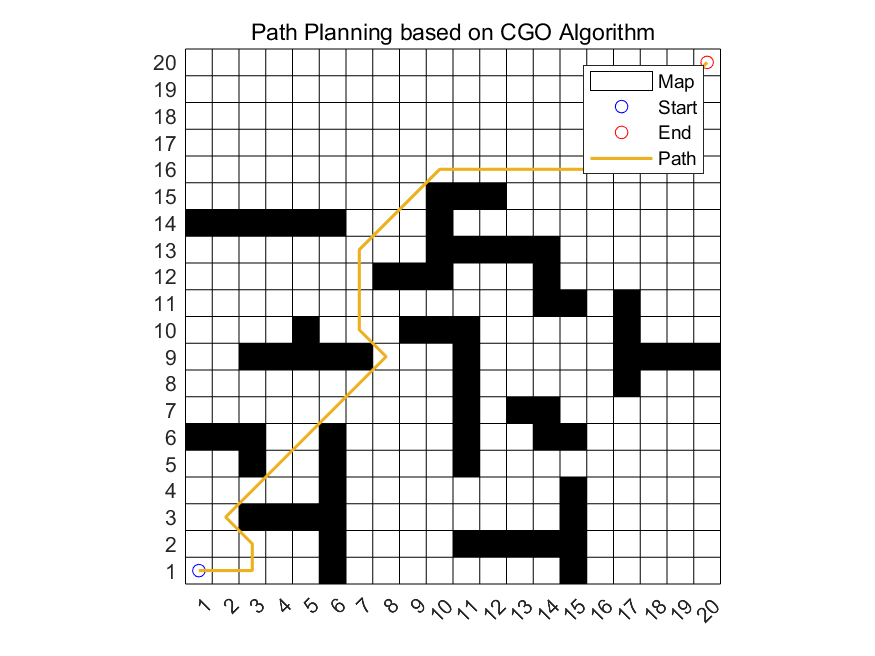
Figure 6. Path planning under a more complicated situation.

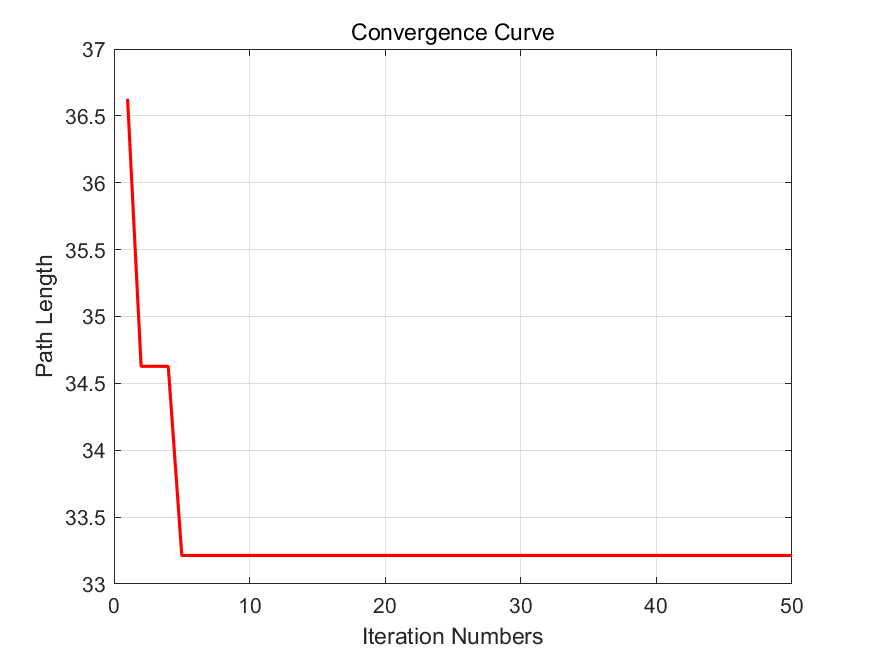
Figure 7. Convergence curve under more complicated situation.

α_i = Rand

orα_i = 2 * Rand

orαi = δ * Rand + 1

orαi = ξ * Rand + (-ξ) (6)

where δ and ξ are random numbers in the interval of [0, 1].

3.1.4. Algorithm Flow.

• Step 1: The random selection approach establishes the initial position of candidate solution X or the initial qualifying point in the search space.

• Step 2: Using the self-similarity of the initial qualifying points, the fitness value of the initial candidate solution is determined.

• Step 3: Establish the global ideal value GB and global optimal qualifying point.

• Step 4: A random selection procedure is used to estimate the average value MG_i for each qualified point X_i in the search space.

• Step 5: Create a temporary Sierpinski triangle using X_i, MG_i, and GB_i as its three vertices for each qualified point X_i in the search space.

• Step 6: Adjust the four seeds' placements for each transient triangle.

• Step 7: Reassess seed positions and update fitness values.

• Step 8: Verify that the maximum number of iterations has been reached. The optimal position and the overall optimal solution are produced if the maximum number of iterations is reached. If not, repeat the calculation in Step 3 before moving on.

3.2. Simulation result

The simulation results show the generated paths and the convergence curve.

Figure 4 and Figure 5 show the result under four randomly generated blocks. The result shows that with three iterations, the optimal path is determined.

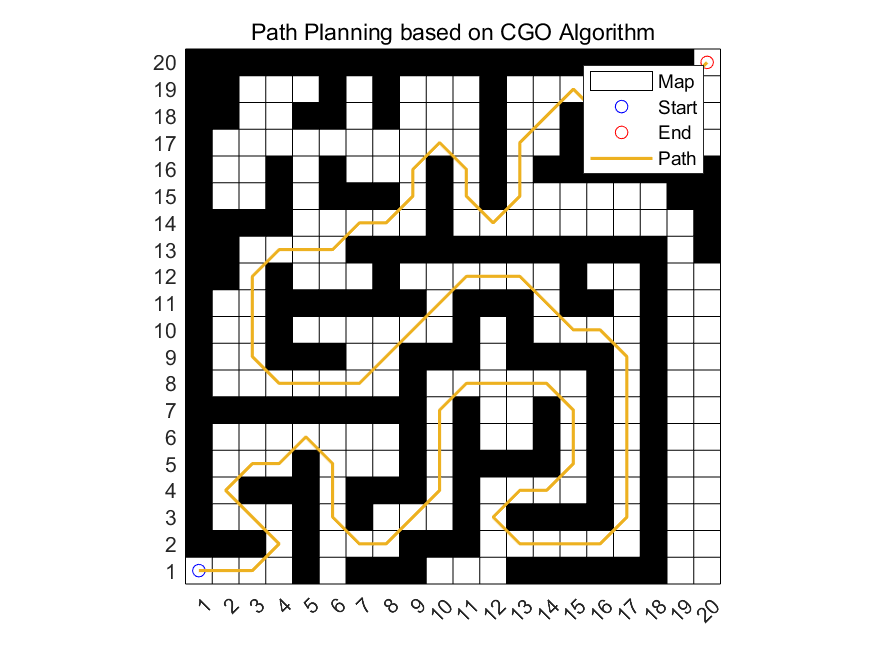
Figure 8. Path planning under a situation of a labyrinth.

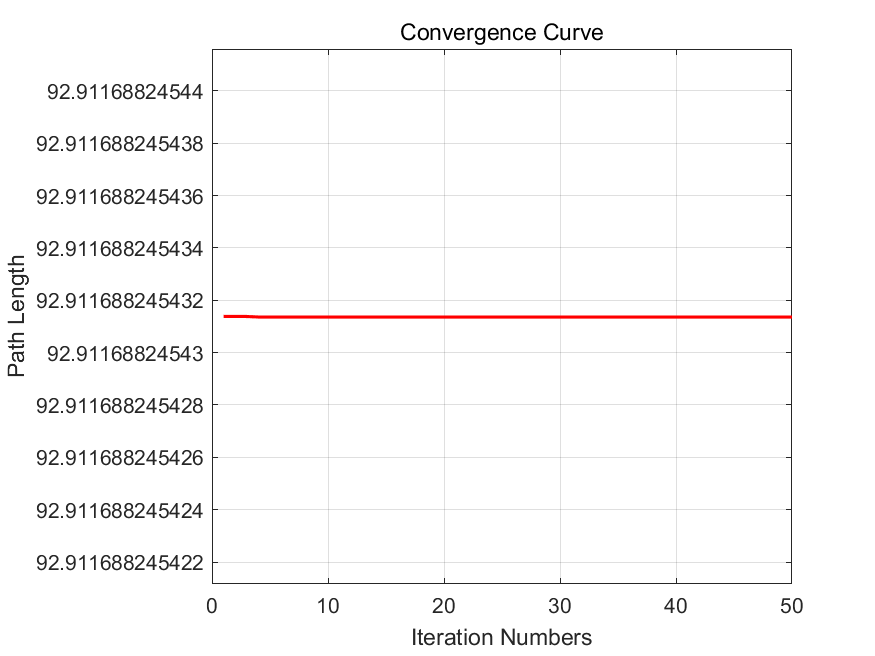
Figure 9. Convergence curve under a situation of a labyrinth.

Figure 6 and Figure 7 present a more complicated situation and the performance under this circumstance. The result shows that with five iterations, the optimal path is determined.

From Figure 4 to Figure 7, we can find that this path planning generator using the CGO algorithm has a relatively high efficiency and speed.

Figure 8 and Figure 9 show an easy labyrinth situation. The result shows that this path planning generator finds the optimal path at the first iteration, which leads to a horizontal line in its convergence curve graph.

4. Conclusion

A novel approach for generating optimal paths based on the Chaos Game Optimization (CGO) method is presented in this study. The CGO algorithm leverages the principles of chaos theory and the chaos game, providing a nature-inspired optimization technique that can handle complex and non-linear optimization problems more efficiently. The CGO algorithm can find better solutions in scenarios with multiple local optima and non-convex objective functions. Moreover, the CGO algorithm incorporates the self-similarity of initial qualifying points and uses a random selection procedure to estimate the average value for each qualified point in the search space. This helps to explore the search space in a random and chaotic manner, increasing the randomness and unpredictability of the generated paths. Additionally, the CGO algorithm can handle complex and dynamic environments, and it can generate optimal paths even in scenarios with randomly generated blocks or complex labyrinth environments. The paper's MATLAB simulation results demonstrate the effectiveness of the CGO algorithm in generating optimal paths.

To sum up, the path planning generator that utilizes the CGO algorithm, as described in this paper, presents a promising method for improving the capabilities of autonomous robots. By utilizing the principles of chaos theory and the chaos game, this generator offers an effective and sturdy solution for path planning in complex and ever-changing environments.

For further work, the performance of different path planning methods can be compared and evaluated with this path planning generator. In this work, the map is built as a 20x20 grid graph. However, it can be larger and more complicated so that the performance of this generator can be evaluated more accurately. The CGO algorithm, with its efficiency, could also be applied to other areas such as motion planning, real-time planning, and so on.