1. Introduction

As data privacy and security issues have received increasing attention worldwide, how to effectively utilize distributed data while protecting personal privacy has become an important research topic. The purpose of federated learning (FL) proposed by Google in 2016 is to resolve data silos and data privacy concerns and has become an innovative solution to this challenge. Federated learning significantly enhances data privacy and security by allowing multiple devices or servers to collaborate to train shared models while keeping data local and avoiding sending raw data to central servers.

In the context of the continuous development of federated learning technology, the impact of the choice of optimization algorithm on model performance has become particularly important. Karimireddy et al. proposed Stochastic Controlled Averaging for Federated Learning (SCAFFOLD), which aims to reduce client drift by controlling random updates, thereby significantly improving efficiency and model performance [1]. Chai et al. studied and discussed the common federated learning algorithms Federated Stochastic Gradient Descent (FedSGD) and Federal Averaging (FedAvg), emphasizing that FedAvg is more effective in reducing communication costs [2]. Federated Proximal (FedProx) proposed by Sahu et al. solves the problems of heterogeneous data and unstable network connections by adding regularization terms, thereby enhancing the stability and performance of federated learning [3]. Nowadays, FedAvg, FedSGD, SCAFFOLD and FedProx are several commonly used and representative federated learning algorithms. These algorithms have their own characteristics. FedAvg optimizes by averaging the model weights of the client, FedSGD optimizes by averaging the gradients of the client, SCAFFOLD and FedProx improve the model performance by corrected optimization and regularization methods respectively. This paper compares and analyzes the performance of these algorithms based on the Fashion-MNIST dataset, which not only helps to understand their advantages and disadvantages, but also provides a strong guide for the selection of algorithms in practical applications.

In addition to these algorithms, there are several other studies that have made significant contributions to the development of federated learning. The FedML framework is discussed for its wide application in real-world scenarios, especially on mobile devices, demonstrating that federated learning can be used broadly and effectively [4]. The application of federated learning in mobile keyboard prediction shows that it can significantly improve prediction accuracy without uploading user data, further emphasizing the privacy advantage of federated learning [5].

Communication efficiency is another key aspect of federated learning. The FedAvg algorithm is known for its communication efficiency in learning deep networks from decentralized data, while reducing communication costs while maintaining high model performance [6].

On the other hand, the Fashion-MNIST dataset, introduced as a more challenging alternative to MNIST, has been widely used in federated learning research to benchmark algorithms [7]. For example, a study using CNN to classify clothing in the Fashion-MNIST dataset showed high accuracy, indicating that federated learning models are capable of handling complex image classification tasks [8,9]. Finally, Konečný et al. explored strategies to improve communication efficiency in federated learning and proposed structured updates and compressed updates, which significantly reduced communication costs while maintaining model performance [10].

The motivation behind this study is to address several key challenges in federated learning, including optimizing model performance, improving communication efficiency, and ensuring robustness in heterogeneous and unstable network environments. By comparing and analyzing various federated learning algorithms, this study aims to provide insights and guidance for selecting the most appropriate algorithm for different practical applications.

Based on the Fashion-MNIST dataset, this paper deeply explores and compares these four commonly used algorithms in federated learning. This paper first implements LSTM, ResNet, CNN, and FCNN in the experiment, and finally selects the CNN model to evaluate the four algorithms of FedAvg, FedSGD, SCAFFOLD, and FedProx through experimental data analysis to comprehensively analyze the performance of each algorithm on the same model. Specifically, this paper evaluates the performance of each algorithm in terms of model convergence speed, accuracy, and communication cost through experiments to explore their potential and applicability in practical applications.

This paper consists of the following main contributions:

1. Implemented a variety of federated learning algorithms (such as FedAvg, FedSGD, SCAFFOLD, FedProx), and conducted experimental comparisons under the same model.

2. Through experiments, the performance differences of different federated learning algorithms on the same model are revealed, their applicability in practical applications is analyzed, and reference data and insights are provided for the selection of federated learning algorithms, supporting algorithm selection in practical applications and further research.

2. Data Exploration and Visualization

Fashion-MNIST is an image dataset that replaces the traditional MNIST handwritten digit recognition dataset. It was proposed by Zalando to provide a more challenging dataset for benchmarking in the machine learning community. The design of Fashion-MNIST is similar to the original MNIST dataset, but instead of handwritten digits there are images from 10 fashion products.

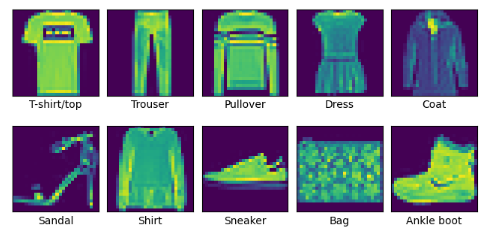
Figure 1. Fashion-MNIST dataset category display [7]

As can be seen from Figure 1, the Fashion-MNIST dataset has 10 categories, including T-shirts/tops, pants, pullovers, dresses, coats, sandals, shirts, sneakers, bags and boots, and each picture is a 28x28 pixel grayscale picture with a pixel value of 0-255.

3. Federated Learning Algorithms

In this section, we will explore several key algorithms for federated learning, each of which addresses unique challenges and optimizes different aspects of the training process. Federated learning is an innovative approach that decentralizes model training, enhances data privacy, and leverages the computing resources of multiple clients. The algorithms discussed in this section - Federated Averaging (FedAvg), Federated Stochastic Gradient Descent (FedSGD), Federated Proximal (FedProx), and Stochastic Controlled Averaging for Federated Learning (SCAFFOLD) - were each selected for their unique approach and ability to handle various issues such as communication cost, data heterogeneity, and model convergence.

These algorithms were selected to provide a comprehensive understanding of the prospects of federated learning, focusing on solutions to common problems such as communication efficiency, data heterogeneity, and the need for robust convergence mechanisms. The unique characteristics and mechanisms of each algorithm make it suitable for different federated learning scenarios, providing researchers and practitioners with a wealth of choices.

3.1. FedAvg Algorithm

3.1.1. Overview. Federated Averaging (FedAvg) is a pivotal algorithm in federated learning that facilitates decentralized model training by leveraging local computations on multiple clients. Initially, a global model is distributed to all clients, who then independently train it on their local datasets. After receiving training in the local setting, clients submit their updated model parameters to a central server, Who calculates a weighted average by utilizing the quantity of data samples for every client used to aggregate these updates. The aggregated parameters update the global model, and this process iterates over multiple rounds until the model converges or meets a predefined stopping criterion. This approach effectively maintains data privacy and reduces the need for data centralization.

3.1.2. Process. As shown in Figure 2, each client first trains a local model on its data for multiple epochs. The updates sent locally are then transferred to the central server. At the end of the process, the server combines these updates to generate a global model.

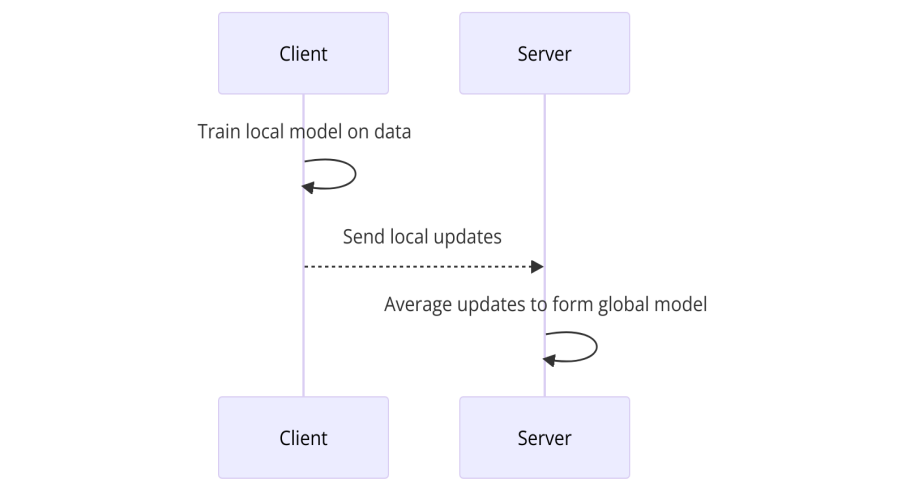
Figure 2. Flowchart of FedAvg algorithm (Photo/Picture credit : Original)

3.1.3. Advantages. Reduce communication cost: By cutting down on the frequency of communication between the server and the client. (by uploading updates after multiple rounds of local iterations), it is suitable for situations with high communication costs or limited bandwidth.

Improve model performance: Since each client can train on local data for multiple cycles before uploading, the model's performance is aided by it.

3.1.4. Disadvantages. Inadequate processing of non-IID data: If there are significant variations in the distribution of client data, parameter averaging alone may not be enough to fully utilize the information of all clients, which may lead to uneven model performance.

3.2. FedSGD Algorithm

3.2.1. Overview. Federated Stochastic Gradient Descent (FedSGD) is a federated learning algorithm where, instead of averaging model parameters, the clients compute and send the gradients of the loss function with respect to their local data to a central server. The server then aggregates these gradients by averaging them and uses the result to change the parameters of the global model. Iterative repetition is used for this process, allowing the global model to be optimized based on the collective gradient information from all clients, thereby enabling model training without requiring direct access to the clients' data.

3.2.2. Process. As shown in Figure 3, before sending the gradient to the central server, each client calculates the change in direction of the local loss function. Finally, these gradients are averaged by the server and the global model is updated.

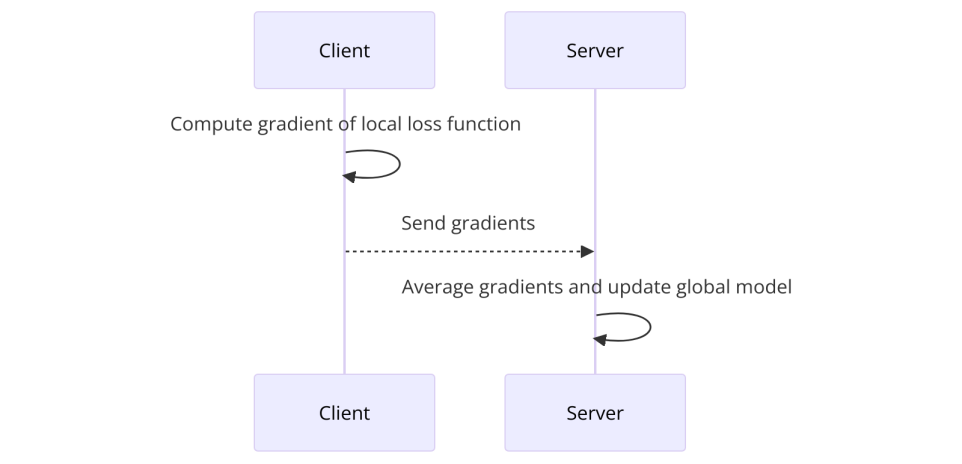
Figure 3. Flowchart of FedSGD algorithm (Photo/Picture credit : Original)

3.2.3. Advantages. Simple implementation: Each client calculates the gradient and then sends it to the central server for averaging, which is relatively straightforward to implement.

Fast response: Suitable for applications that require fast model updates.

3.2.4. Disadvantages. High communication cost: Gradients need to be uploaded every time a local calculation is completed, which is not friendly to applications that are sensitive to communication costs.

Poor processing of non-IID data: Directly averaging gradients may not handle the heterogeneity of client data well.

3.3. FedProx Algorithm

3.3.1. Overview Federated Proximal (FedProx) extends the FedAvg algorithm to better manage heterogeneous data across clients by incorporating a proximal term in the local objective function, which acts as a regularizer. This proximal term penalizes the difference in updates for the local model from the global model, thereby stabilizing training and improving convergence when clients' data distributions and computational capabilities are diverse. This makes FedProx particularly effective in real-world federated learning scenarios where client data is non-IID (non-Independent and Identically Distributed) and clients may have varying amounts of computational power and data.

3.3.2. Process. As can be seen from Figure 4, it is similar to FEDAVG, but the issue of client variation is solved by incorporating a proximal term into the local objective. Secondly, the regularization term penalizes large deviations from the global model.

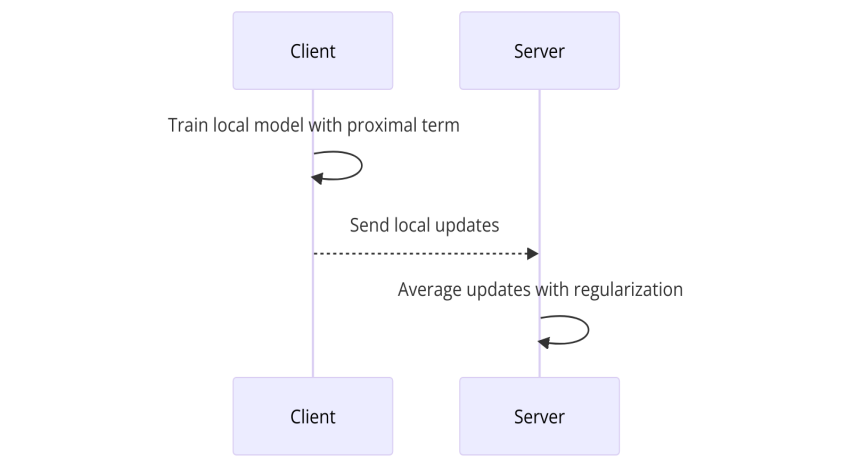
Figure 4. Flowchart of FedProx algorithm (Photo/Picture credit : Original)

3.3.3. Advantages. Adapt to data heterogeneity: Adding regularization terms (surrogate terms) to local loss functions helps deal with uneven data distribution.

Stabilize the training process: Regularization terms can reduce the differences in model updates of individual clients, making global model updates smoother and more stable.

3.3.4. Disadvantages. Regularization parameter adjustment: The strength of the regularization term needs to be carefully selected, which may require experimentation and adjustment based on the specific application.

May affect model flexibility: Too strong regularization may limit the model from learning useful patterns unique to the client.

3.4. SCAFFOLD Algorithm

3.4.1. Overview. Stochastic Controlled Averaging for Federated Learning (SCAFFOLD) is an advanced algorithm that addresses the client drift issue, which arises due to the heterogeneity of data and local updates in federated learning. SCAFFOLD uses control variates, which are corrective terms, to adjust the local updates and mitigate the divergence between local and global models. Each client maintains a control variate that captures the variance among its local and global gradients, and this control variate is used to correct the local model updates. By doing so, SCAFFOLD ensures that the aggregated updates are more consistent and aligned with the global objective, thereby improving convergence and performance in federated learning environments with highly diverse data distributions.

3.4.2. Process. As can be seen from Figure 5, each client first uses the control variables to correct the local model update, and then the server also maintains and updates these control variables. Finally, the advantages of local SGD and control variables are combined to achieve more accurate updates.

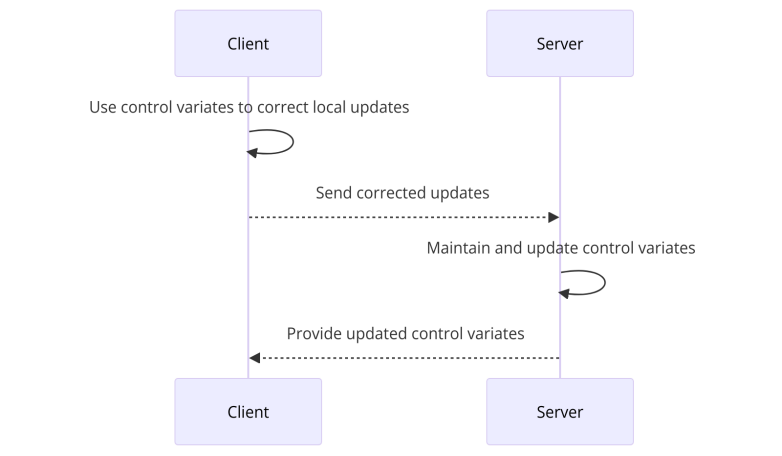
Figure 5. Flowchart of SCAFFOLD algorithm (Photo/Picture credit : Original)

3.4.3. Advantages. Solve client bias: Correcting client updates by control variables can effectively solve the model drift problem caused by non-IID data.

Improve model convergence speed and accuracy: Optimize model updates through correction mechanisms, speed up convergence, and improve prediction accuracy.

3.4.4. Disadvantages. High algorithm complexity: Additional control variables need to be maintained, which increases the complexity and computational burden of implementation.

More tuning may be required: In order to achieve optimal performance, the use and update strategy of control variables may need to be carefully adjusted.

4. Experimental Result

4.1. Experimental setup

Scale pixel values to [0, 1]. Federated learning settings:Training rounds are set to 10 and the number of clients is set to 5. Optimizer and loss function:Use Adam optimizer and sparse_categorical_crossentropy loss function.

4.2. Experimental evaluation indicators

Model evaluation involves not only using the test set to test the accuracy of the model, but also multiple metrics to gain insight into the performance of the model in different aspects. This article uses the test set data to calculate the following metrics.

4.2.1. Model accuracy:Reflects the model's ability to correctly predict test set samples. Model Precision:Measures the proportion of true positive predictions among all positive predictions.

4.2.2. Model recall:Assesses the model's ability to identify true positive samples. Model F1 Rate:Combines precision and recall to evaluate the model's overall performance.

5. Model Selection (based on FedSGD algorithm)

5.1. Evaluation metrics analysis

This study conducted a detailed analysis of the performance of different models on the Fashion-MNIST dataset.This paper analyzes the LSTM, ResNet, FCNN, and CNN models based on experimental data. The analysis and comparison of the data in Table 1 indicates that:

Table 1. Model testing outcomes

5.1.1. Accuracy. The observation reveals that among the evaluated models, the FCNN with an accuracy of 0.8106 and the CNN with an accuracy of 0.8092 demonstrate the highest performance, significantly surpassing the LSTM with an accuracy of 0.7323 and the ResNet with an accuracy of 0.7204. The superior performance of FCNN and CNN can be attributed to their efficacy in feature extraction and the capture of spatial hierarchies, which are critical for image classification tasks such as the Fashion-MNIST dataset. In contrast, the LSTM's design, tailored for sequential data, and the overcomplexity of ResNet for this relatively simple dataset, have led to suboptimal accuracy.

5.1.2. Precision. The observation indicates that FCNN achieves the highest precision at 0.8236, closely followed by CNN with a precision of 0.8122. In comparison, LSTM and ResNet exhibit lower precision scores at 0.7474 and 0.7628, respectively. The exceptional effectiveness of FCNN and CNN can be ascribed to their aptitude in efficiently extracting and utilizing local features within the picture data. This capability is vital for catching the intricate nuances and spatial connections required for precise categorization. On the other hand, LSTM, designed for sequential data processing, may not efficiently handle the spatial nature of image data, leading to less accurate predictions. ResNet, although capable of learning hierarchical features, may suffer from overfitting or excessive complexity for the relatively simple structure of the Fashion-MNIST dataset.

5.1.3. Recall. The observation shows that FCNN achieves the highest recall at 0.8106, closely followed by CNN with a recall of 0.8092. In comparison, LSTM and ResNet exhibit lower recall scores at 0.7330 and 0.7204, respectively. The superior recall performance of FCNN and CNN indicates their robustness in identifying true positive samples, which is crucial for accurate image classification. In contrast, LSTM, designed for sequential data processing, and ResNet, which may face complexity issues, struggle to match the recall performance of FCNN and CNN.

5.1.4. F1-score. The observation shows that FCNN leads in F1-score with 0.8129, followed by CNN at 0.8055. In contrast, LSTM and ResNet have lower F1-scores of 0.7283 and 0.7096, respectively. The strong F1-scores of FCNN and CNN reflect their balanced precision and recall, making them well-suited for Fashion-MNIST tasks. The lower F1-scores of LSTM and ResNet are due to their lower precision and recall, stemming from their design focus and complexity issues, respectively, as discussed earlier.

5.2. Visual analysis of model results

In addition to the above indicator analysis, this paper also realizes the visualization of its accuracy results, as shown in Figure 6.

Figure 6. Comparing the accuracy of various models during training sessions (Photo/Picture credit : Original)

In experiments with FedSGD training, the four models showed varied performance on the Fashion-MNIST dataset. The ResNet, due to its complexity, suffered from overfitting and did not effectively utilize local data, leading to large accuracy fluctuations and a downward trend overall. The LSTM, designed for sequence data, struggled with image processing, yielding stable but unimpressive results. By comparison, the FCNN and CNN models demonstrated both stability and high accuracy, thanks to their proficiency in extracting local features and learning spatial hierarchies, which gave them an edge in image classification.

6. Algorithm Comparison (based on CNN model)

6.1. Algorithm Performance Analysis in Federated Learning

This study conducted a detailed analysis of the performance of different federated learning algorithms on the Fashion-MNIST dataset, and ultimately found that the FedProx algorithm was the most effective in predicting the Fashion-MNIST dataset. This article will analyze the Federal Averaging (FedAvg), Federated Stochastic Gradient Descent (FedSGD), Stochastic Controlled Averaging for Federated Learning (SCAFFOLD), and Federated Proximal (FedProx) algorithms in the form of group comparison.

Table 2. Algorithm results comparison

Upon analyzing and comparing the data presented in Table 2, significant disparities in the performance of various federated learning algorithms on the Fashion-MNIST dataset become apparent. Regarding accuracy, FedProx achieves the highest score at 0.9159, followed closely by SCAFFOLD at 0.8998, FedAvg at 0.8995, and FedSGD trailing with 0.7943. The superior accuracy of FedProx can be attributed to its regularization of the proximal term, which enhances stability and consistency across clients with diverse data distributions.

In terms of precision, FedProx again leads with a score of 0.9156, closely followed by SCAFFOLD at 0.9007, FedAvg at 0.8992, and FedSGD with a lower precision at 0.8026. The regularization approach of FedProx effectively addresses variations in client data distributions, thereby improving precision. SCAFFOLD's use of control variates reduces client drift, resulting in a slight precision advantage over FedAvg.

For recall, FedProx maintains the highest rate at 0.9159, with SCAFFOLD at 0.8998 and FedAvg at 0.8995 following behind, while FedSGD exhibits the lowest recall at 0.7943. The robust recall of FedProx suggests its effectiveness in identifying true positives, a testament to the impact of its proximal term design.

Finally, in terms of the F1 score, FedProx secures the highest value at 0.9155, with SCAFFOLD at 0.9001 and FedAvg at 0.8989 showing similar performance, and FedSGD lagging with the lowest F1 score at 0.7855. FedProx's balanced performance in precision and recall contributes to its optimal F1 score. SCAFFOLD's corrective terms and FedAvg's multi-step local training both play a role in enhancing their F1 scores. In contrast, FedSGD's lack of comprehensive local training leads to suboptimal F1 scores, highlighting its overall performance deficit.

6.2. Discussion

The performance of these federated learning algorithms is largely determined by their ability to handle the non-IID nature of client data and the extent of local training allowed before aggregation. FedSGD, the worst performer, uses a simplistic approach with a single gradient update per client, leading to slow convergence and poor generalization. FedAvg, which performs multiple local updates, significantly improves convergence and performance, reducing communication overhead and better adapting to local data. SCAFFOLD theoretically offers better bias correction through control variates, but its actual performance gain over FedAvg is minimal, indicating that for datasets like Fashion-MNIST, FedAvg's multiple local updates are already highly effective. FedProx, the best performer, uses a regularization approach to stabilize training by limiting the deviation of local updates, ensuring consistent model updates across clients with diverse data distributions, thereby significantly enhancing performance and robustness in federated learning scenarios.

7. Conclusion

This study compares four federated learning algorithms (FedAvg, FedSGD, SCAFFOLD, and FedProx) on the Fashion-MNIST database and shows the performance differences of these algorithms in different models. This article discovers that algorithms that more efficiently process non-IID data, such as multiple local updates (FedAvg) and normalization (FedProx), are often better represented. In comparison, FedSGD has certain advantages in terms of processing data variability, while SCAFFOLD has advantages in regards to enhancing model stability and dealing with data that is not IID. As explained above, the Union learns computational choices by thoroughly considering data features and application scenarios to find the best balance between probability, stability and communication.

This paper compares the performance of federated learning algorithms on homogeneous data sets and models, addressing gaps in algorithm selection research. It aids researchers in choosing suitable methods, enhancing model training efficiency. While focused on the Fashion-MNIST dataset, the findings may apply broadly. For evenly distributed data, FedAvg is preferable; for high variability, FedSGD, SCAFFOLD, and FedProx are more suitable. Limitations include the dataset scope, necessitating future research on diverse data types and scenarios. Further optimization strategies will be explored to reduce communication costs and improve training efficiency, promoting wider adoption of federated learning.