1. Introduction

Introduced by Goodfellow et al. in 2014, Generative Adversarial Networks (GAN) consist of two neural networks: the discriminator and the generator. More specifically, the generator will generate data from the training dataset, and the discriminator will distinguish between produced and actual data [1]. The networks are trained in a minimax game where the generator tries to fool the discriminator, and the discriminator seeks to correctly discriminate between actual and fake data. Since they were first introduced, they have been used to develop amazing projects, such as generating images, improving the resolution of images, and predicting missing information [2,3]. While these GANs and their competing generator and discriminator models have been able to achieve great success, there have been several drawbacks of the network.

J-S divergence is commonly used to measure the difference between the generated and real data distributions when utilizing classic GANs. On the other hand, when the discriminator is overly powerful, J-S divergence may result in vanishing gradients, which could lead to training instability. Furthermore, the generator of a typical GAN produces a restricted range of samples, a phenomenon known as model collapse. In the case of convergence failure, the model fails to produce optimal or high-quality results. In the case of pattern collapse, the model fails to produce unique images that repeat similar patterns or qualities [4].

To improve traditional GANs, Wasserstein GAN (WGAN) was introduced by Arjovsky, M., Chintala, S., & Bottou, L. in 2017 [5]. The Wasserstein distance—also referred to as the Earth-mover distance—is used by WGAN. A more useful indicator of distribution similarity is the Wasserstein distance, which calculates the least amount of mass that must be transported to change one distribution into another. This approach provides a more meaningful measure of distribution similarity and offers several advantages over traditional GANs. Although WGAN is better than traditional GAN, it also has a problem. Weight clipping is not a useful technique for enforcing a Lipschitz limitation [6]. It could take some time for the weights to reach their limits when the clipping parameter is large, which makes it challenging to train the critic to optimality. On the other hand, vanishing gradients may result from small clipping parameters, particularly in deep networks or in situations where batch normalization is not used.

The gradient penalty was proposed as a better way to enforce the Lipschitz constraint and lessen the problems caused by weight clipping in WGANs. Weight clipping has drawbacks that are addressed by gradient penalty, which penalizes the model directly if the gradient norm deviates from a given value, usually set to 1. This guarantees that the gradients stay within a predetermined range, which enhances training stability.

2. Method

WGAN is an improvement over the standard GAN designed to address some of the training difficulties associated with GANs, such as instability and mode collapse. Instead of employing the Jensen-Shannon divergence, WGAN measures the difference between the created and real data distributions using the Wasserstein distance, also known as Earth Mover's Distance. As a result, training experiences a smoother and more meaningful gradient, which aids in improving convergence and stability. In WGAN, a critic takes the position of the discriminator. A score proportionate to the Wasserstein distance between the generated and real distributions will be produced by the critic. The goal of the critic is to increase this separation.

Weight clipping in GAN (GAN-CP) is a neural network training approach where the weights of the network are clipped to lay within a given range. This means that after each update during the training process, the weights are adjusted to ensure they fall within the predefined minimum and maximum values. In Wasserstein GAN training, one well-known method for regulating the critic's Lipschitz constant is weight clipping. The critic's parameters are all clipped to a predetermined range after each training iteration, which has an impact on the optimizer's performance [6]. However, weight clipping also has some drawbacks, if the clipping parameter is too large, the weights may not be constrained effectively. This makes it more difficult for the network to enforce the Lipschitz constraint and stabilize training. Enforcing a Lipschitz constraint with weight clipping is inefficient. It is challenging to train the critic as effectively as possible when the clipping parameter is huge since it takes a while for the weights to approach their limitations. On the other hand, vanishing gradients may result from a small clipping value, particularly in deep networks or in situations where batch normalization is not applied [5]. Therefore, this work introduces the gradient penalty to optimize the training process.

Gradient penalty in GAN (GAN-GP) is used in WGANs to subject the critic (or discriminator) to the Lipschitz constraint. It acts as a substitute for weight clipping, which has several disadvantages [7]. By penalizing the norm of the gradients of the critic's output with regard to its input, the gradient penalty technique promotes more effective and consistent training. For every training iteration, find the gradient between the critic's input and output. Usually, this is carried out for points produced by the generator and points that are sampled from the data distribution. A differentiable function f is 1-Lipschitz if and only if it has gradients with norm at most 1 everywhere.

For f, the gradient norm of the points that were interpolated between the generated and actual data should be 1. WGAN-GP penalizes the model if the gradient norm diverges from the goal norm value of 1 rather than applying clipping. In addition, the discriminator (critic) avoids batch normalization because it establishes correlations between data in the same batch. Experiments confirm that this has an impact on the gradient penalty's efficacy [8].

3. Experiment and Result

3.1. Dataset

For the experiments, the author utilized the Fashion Modified National Institute of Standards and Technology (MNIST) and Canadian Institute for Advanced Research (CIFAR)-10 datasets [9,10]. The Fashion MNIST dataset consists of 70,000 grayscale photos of fashion items at 28x28 pixels. The CIFAR-10 dataset contains 60,000 color, 32x32 pixel images divided into 10 categories.

The quality of images generated by WGAN-GP was consistently higher than those produced by WGAN-CP. One notable disadvantage of WGAN-GP was the longer training time. The addition of the gradient penalty term significantly increased the computational complexity.

3.2. Training Detail

The Pytorch version used in the experiment is 2.4.0. Several significant hyperparameters are used in this WGAN-CP implementation to improve the training procedure. A gradual and steady learning pace is ensured by setting the learning rate to 0.00005. 64 is the batch size used for training, which strikes a balance between training stability and computing efficiency. To keep the gradients of the critic under the Lipschitz restriction, a weight clipping limit of 0.01 is applied. Five critic iterations follow each generator iteration, enhancing the critic's capacity to distinguish between generated and true data. Because it works well in this particular GAN variation, the RMSprop optimizer is used for both the generator and the discriminator.

In this implementation of the WGAN-GP, several key hyperparameters are used to optimize the training process. The learning rate is set to 0.0001, facilitating a balanced pace of learning. The Adam optimizer is employed with betas of (0.5, 0.999), ensuring effective momentum and variance control during optimization. The model trains using a batch size of 64, providing a good balance between training stability and computational efficiency. Five critic iterations follow each generator iteration, improving the critic's capacity to discern between created and genuine data. Furthermore, a gradient penalty lambda term of 10 is introduced, which strengthens the enforcement of the Lipschitz constraint and promotes stable training dynamics.

Figure 1. Generated images on CIFAR-10 dataset (Figure Credits: Original).

3.3. Result Comparison

The results demonstrate a trade-off between generated image quality and training duration. While WGAN-CP benefits from faster training times, it often suffers from instability and lower-quality outputs. On the other hand, WGAN-GP, despite its longer training time, provides more stable training and higher quality images. The improved performance of WGAN-GP can be attributed to the gradient penalty, which better enforces the Lipschitz constraint compared to weight clipping in WGAN-CP. This leads to more robust training dynamics and superior image quality.

In practical applications, the choice between WGAN-CP and WGAN-GP may depend on the specific requirements. For scenarios where training time is critical, WGAN-CP might be preferred. However, for applications demanding high-quality outputs, WGAN-GP is the superior choice despite the increased computational cost.

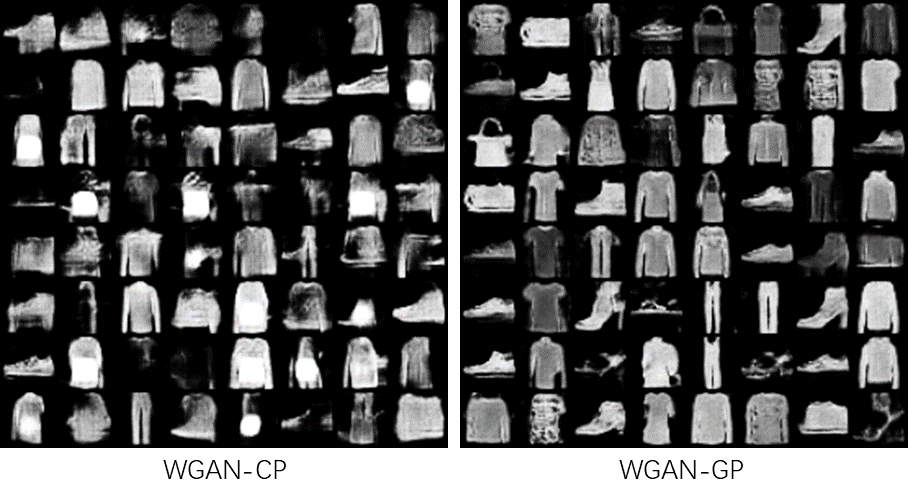
Figure 2. Generated images on Fashion MNIST dataset (Figure Credits: Original).

4. Discussion

To address problems like mode collapse and training instability, WGAN is an enhanced version of GAN. Both WGAN-CP and WGAN-GP are variations of WGAN that use distinct methods to impose the Lipschitz constraint required for the Wasserstein distance.

Weight clipping is WGAN-CP's method of enforcing the Lipschitz constraint, which guarantees restricted gradients for the critic (discriminator) function. The advantage of WGAN-CP includes simplicity and computational efficiency. In specific, weight clipping is straightforward to implement and the training is faster due to the simplicity of weight clipping. It does, however, also have certain drawbacks. These include training instability and picture quality, which implies that, in comparison to more sophisticated methods, the training process's stability and image quality may not be at their best. The reason is that weight clipping can lead to training instability and suboptimal performance. The clipping parameter needs to be finely tuned; too large a value fails to enforce the Lipschitz constraint effectively, while too small a value can led to vanishing gradients.

On the other hand, WGAN-GP applies the Lipschitz constraint with the help of the gradient penalty rather than weight clipping. The gradient penalty method in WGAN-GP has several benefits, such as better convergence and smoother gradients due to its effective enforcement of the Lipschitz constraint, which also improves training stability. Additionally, the model performance is superior, with generally higher quality generated images and more stable training dynamics compared to WGAN-CP. However, there are also some disadvantages. The computational complexity is higher, as calculating the gradient penalty is resource-intensive and leads to longer training times. Furthermore, the implementation is more complex, requiring careful tuning of the lambda term to achieve optimal results.

In short, both WGAN-CP and WGAN-GP have their unique strengths and weaknesses. WGAN-CP is simpler and computationally efficient but may suffer from training instability and lower-quality outputs. In contrast, WGAN-GP has more stable training and better image quality at the cost of increased computational complexity and longer training times. The choice between WGAN-CP and WGAN-GP should be guided by the specific requirements of the application, such as the importance of training stability, image quality, and computational resources available.

5. Conclusion

This work specifically compares the WGAN-CP and WGAN-GP WGAN models. The research done using the Fashion MNIST and CIFAR-10 datasets makes it evident that every strategy has certain advantages and drawbacks. Weight clipping is utilized by WGAN-CP to enforce the Lipschitz constraint, making it easier to construct and more computationally efficient, resulting in faster training times. However, this simplicity may come at the expense of less-than-ideal image quality and possible training instability since the approach might not properly enforce the Lipschitz constraint, which could result in problems like vanishing gradients. In terms of training stability and generated image quality, WGAN-GP performs better than other methods since it employs a gradient penalty. Gradients are smoother and convergence is more stable when the gradient penalty approach is used to impose the Lipschitz constraint more successfully. However, this approach is computationally more demanding and requires careful tuning of the lambda term, leading to longer training times.

In conclusion, the choice between WGAN-CP and WGAN-GP should be guided by the specific needs of the application. If computational efficiency and simplicity are paramount, WGAN-CP may be the preferred choice. However, for applications where the quality of the generated output and training stability are critical, WGAN-GP is likely the better option despite the increased computational cost. Future work may explore hybrid approaches or further optimizations to balance these trade-offs more effectively.