1. Introduction
In astronomical research, high-quality images are crucial for accurate observation and analysis of celestial objects [1]. However, astronomical images are often affected by sensor noise, which can degrade image clarity and lead to errors in scientific data interpretation [2-3]. Thus, effectively removing sensor noise[3] to enhance image quality is a key challenge in astronomical image processing. Traditional denoising methods often struggle to balance noise reduction with detail preservation, especially when handling the complexities of astronomical images [2]. Therefore, developing techniques that can achieve this balance is of great importance. The focus of this study is to develop a deep learning-based approach to improve the quality of astronomical images. This research proposes an enhanced Pix2Pix generative adversarial network model that incorporates Residual Blocks and Self-Attention mechanisms to boost performance in denoising tasks [4-7]. While Pix2Pix has shown promise in various image transformation tasks, incorporating Residual Blocks helps mitigate the vanishing gradient problem in deep networks, capturing finer details of the images. Meanwhile, the Self-Attention mechanism allows the model to capture global information more effectively, leading to improved denoising results [8]. This study compares the denoising capabilities of five different techniques: traditional denoising methods, standard Pix2Pix, Pix2Pix with Residual Blocks, Pix2Pix with Self-Attention, and Pix2Pix with both Residual Blocks and Self-Attention. The author evaluates these methods using Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) as performance metrics [9-10]. The results demonstrate that the Pix2Pix model, enhanced with Residual Blocks and Self-Attention, significantly outperforms other methods in both noise reduction and detail preservation. This research offers an effective solution for high-quality processing of astronomical images, contributing to more accurate astronomical data analysis.
2. Literature review
In the field of astronomical image denoising, traditional methods such as mean filtering, Gaussian filtering, and median filtering have been widely used. While these techniques reduce noise by smoothing the image, they often lead to the loss of important image details. More sophisticated methods like wavelet transform denoising and Non-Local Means have shown effectiveness in specific scenarios, but they struggle to balance noise reduction and detail preservation when handling complex astronomical images. The advent of Generative Adversarial Networks (GANs), particularly the Pix2Pix model, has introduced significant advancements in image denoising. Pix2Pix, as a conditional GAN model, has been successfully applied to various image processing tasks, including denoising and image restoration. However, despite its success in generating high-quality images, Pix2Pix can face limitations in complex noise environments, particularly in simultaneously removing noise and preserving fine image details. To enhance denoising capabilities, the introduction of Residual Blocks in deep learning models has proven beneficial. Residual Blocks, with their skip connections, effectively mitigate the problem of vanishing gradients in deep networks, allowing for successful training of deeper architectures. In denoising tasks, Residual Blocks help improve noise reduction while retaining subtle image structures, as demonstrated in Gurprem Singh's ResDNN: deep residual learning for natural image denoising [11]. At the same time, the application of Self-Attention mechanisms in image processing has gained considerable attention. Self-Attention enables models to focus on different regions of an image, capturing richer global information. This mechanism has been shown to effectively remove noise while preserving critical image details, as seen in works like Meng Li's SACNN and Zheming Zuo's IDEA-Net [12-13]. Consequently, Self-Attention has demonstrated significant potential in image generation and restoration tasks. Recent research has begun to explore the integration of Residual Blocks and Self-Attention mechanisms in deep learning models to enhance image processing performance. This combination leverages the local detail-preserving capability of Residual Blocks and the global information capture of Self-Attention, offering a more robust approach to image denoising. For instance, models like Long-Chen Shen's SAResNet and Huibin Zhang's RatUNet have shown the benefits of this integration [14-15]. This innovative combination provides a new perspective on image processing, helping to achieve a better balance between detail preservation and noise reduction.
This study will propose an improved Pix2Pix model that integrates Residual Blocks and Self-Attention mechanisms, specifically optimized for reducing sensor noise in astronomical images. Compared to existing denoising methods, our approach enhances the Pix2Pix architecture to effectively remove noise while preserving maximum image details. This method offers a robust solution for high-quality astronomical image processing, supporting more precise scientific data analysis.
3. Methodology
The dataset used in this study consists of TIF-format astronomical images provided by the European Space Agency (ESA) [16]. These images are high-resolution and contain various levels of sensor noise, making them ideal for testing and evaluating different denoising methods. By utilizing ESA's official dataset, the author ensures the quality and reliability of the images, providing a solid foundation for our denoising experiments [16].
During the preprocessing phase, the original images were cropped to a size of 256x256 pixels to standardize input dimensions and improve the efficiency of model training. Each type of noise was added using specific functions that generate noise based on parameters such as mean, standard deviation, and blending coefficients. As a result, two distinct image sets were created: one set of noise-free images, serving as a reference and target output, and another set with artificially added noise, used to train the model to learn effective noise reduction.
The model used in this study is an enhanced version of the Pix2Pix generative adversarial network (GAN), specifically designed for astronomical image denoising. This model integrates Residual Blocks and Self-Attention mechanisms into the traditional Pix2Pix architecture to improve its ability to reduce noise while preserving image details.
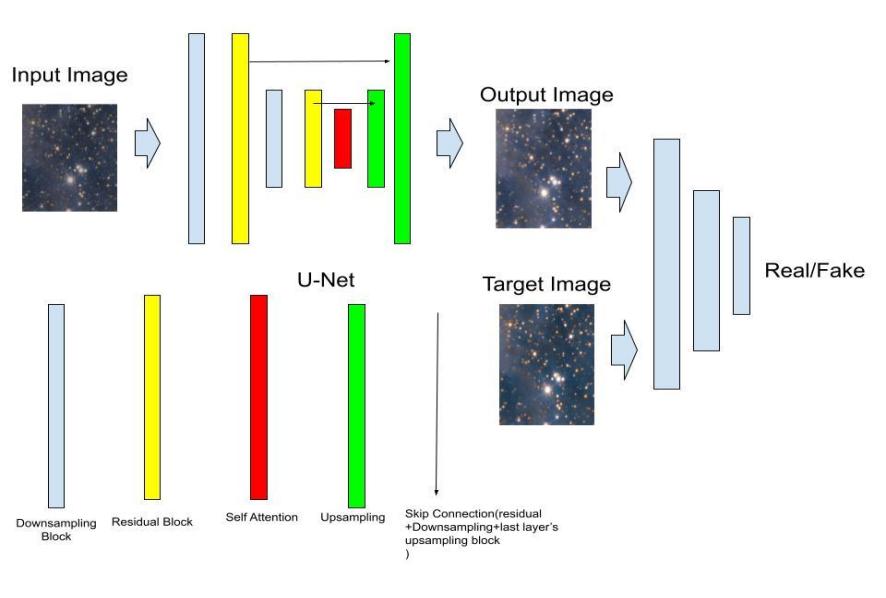
Figure 1. Model Structure.
Figure 1 shows the overall architecture of the model, which includes both the generator and the discriminator components. The generator is constructed using a series of convolutional and transposed convolutional layers, augmented with Residual Blocks and Self-Attention layers. The network begins with an initial down-sampling layer, followed by multiple encoding layers, each composed of a Block module. These block modules consist of convolutional layers, instance normalization, and activation functions (ReLU or Leaky ReLU), designed to extract and encode features at various scales [17-21].
To enhance the model's capability to capture intricate details and handle noise, Residual Blocks are introduced after each encoding step. These blocks, by incorporating shortcut connections, help retain high-frequency information and address the vanishing gradient problem. A key innovation in this model is the inclusion of a Self-Attention layer within the bottleneck structure of the generator. This layer enables the model to focus on different regions of the image, capturing long-range dependencies and global context, which are crucial for effectively distinguishing noise from meaningful structures in astronomical images. Additionally, a Residual Block with Layer Normalization is employed to stabilize training and ensure effective feature scaling [22].
On the decoding side, the network uses up-sampling layers to gradually reconstruct the image from the encoded features. These layers utilize transposed convolutional operations to increase resolution, combined with outputs from previous encoding layers via skip connections, ensuring the preservation of spatial information. The final layer of the generator applies a Tanh activation function to produce an output image with pixel values normalized between -1 and 1[23].
The discriminator is designed to differentiate between real (noise-free) and generated (denoised) images. It takes both the input image and the output of the generator as inputs, concatenates them, and processes them through a series of convolutional layers. Each layer increases the number of feature maps while reducing spatial dimensions, effectively extracting features to determine the authenticity of the images. The final layer outputs a single-channel feature map, indicating the probability that regions of the image are real or generated.
3.1. Training strategy and loss functions
During training, the optimization alternates between the generator and the discriminator. The discriminator aims to maximize its ability to distinguish between real and denoised images, while the generator is trained to minimize a combination of binary cross-entropy loss from the discriminator's output and the L1 loss with respect to the ground truth images. This combined loss ensures that the generator not only fools the discriminator but also produces images that closely resemble the actual noise-free images. Specifically, the discriminator's loss function ( \( {L_{D}} \) ) is defined as:
\( {L_{cGAN}}(G,D)={E_{y}}[logD(y)]+{E_{x,z}}[log(1-D(x,G(x,z))] \) \( (1) \)
where D represents the discriminator, x is the input noisy image, y is the target noise-free image, and G(x,z) is the denoised image generated by the generator.
The generator's loss function ( \( {L_{G}} \) ) combines adversarial loss and L1 loss to ensure the generated images are both realistic and close to the ground truth:
\( {L_{cGAN}}(G,D)={E_{x,y}}[logD(x,y)]+{E_{x,z}}[log(1-D(x,G(x,z))]+ λ({E_{x,y}}[‖y-G(x,z)‖1] \) \( (2) \)
where 𝜆 is a weighting parameter that balances the impact of adversarial loss and L1 loss.
Final goal function is:
\( {G^{*}}=arg{\frac{min}{G}\frac{max}{D}{L_{cGAN}}(G,D)+λ{L_{L1}}(G)} \) \( (3) \)
Furthermore, to stabilize the training process and accelerate convergence, optimization techniques such as learning rate scheduling and gradient scaling are employed. These strategies help the model produce high-quality denoised images while maintaining training stability and convergence speed.
3.2. Experimental environment
The experiments were conducted on a system equipped with an NVIDIA RTX 4090 GPU and an AMD Ryzen 9 7950X CPU, paired with 48GB of DDR5 RAM running at 5200 MHz. The operating system used was Windows 11. The deep learning models were implemented using PyTorch version 2.3.1, with CUDA version 11.8 and cuDNN version 8.2 for GPU acceleration. Additional Python libraries such as NumPy, OpenCV, and TensorBoard were employed for data manipulation, image processing, and visualization. The Pix2Pix model implementation was based on the GitHub repository by Aladdin Persson, which was further extended and customized to meet the specific requirements of this study [24]. The use of these specific hardware and software configurations ensured efficient training and testing of the models, providing consistent and reproducible results.
4. Experiment design and analysis
4.1. Training flow
The training process for the enhanced Pix2Pix model is structured to ensure effective learning and convergence. The dataset is first split into training and validation sets. In each training iteration, the discriminator and generator are updated alternately to improve their respective performances. The discriminator is provided with both real (noise-free) images and fake (denoised) images. The real images are paired with their corresponding noisy images, while the fake images are generated by passing the noisy images through the generator. The discriminator's task is to correctly identify the real images and distinguish them from the generated ones. It evaluates both sets and updates its weights based on the calculated loss, which measures its ability to differentiate between real and fake images. After the discriminator's update, the generator is trained to generate images that can successfully deceive the discriminator. It takes noisy images as input and produces denoised images, which are then evaluated by the discriminator. The generator's loss is calculated based on its ability to deceive the discriminator and how closely the generated images resemble the actual noise-free images, using L1 loss for this purpose. The generator's weights are updated to minimize this combined loss. This process is repeated over multiple epochs to continuously improve the performance of both the generator and the discriminator. Periodic evaluations on the validation set are conducted to monitor the model’s performance and prevent overfitting, ensuring the selection of the best-performing model.
4.2. Optimization methods
To ensure efficient training and faster convergence, several optimization techniques are employed. The Adam optimizer is used for updating the weights of both the generator and discriminator. Adam is preferred for its ability to handle sparse gradients and noisy gradients, combining momentum and adaptive learning rate adjustment to facilitate faster convergence. Learning rate scheduling is implemented to further enhance the model's performance. Techniques such as Cosine Annealing are used to dynamically adjust the learning rate during training [25]. This helps in finding the optimal learning rate at different stages of training, avoiding local minima and accelerating convergence [25]. Additionally, gradient clipping and scaling techniques are applied to address the issues of exploding and vanishing gradients commonly encountered in GAN training. Gradient clipping limits the maximum norm of gradients, while mixed-precision training with gradient scaling improves training stability and efficiency.
4.3. Result presentation
As shown in table 1, the data indicates that incorporating residual blocks and self-attention mechanisms into the standard Pix2Pix model significantly enhances image denoising performance. Particularly, the version with residual blocks alone performs exceptionally well in both PSNR and SSIM, demonstrating its effectiveness in improving image quality. While the combination of residual blocks and self-attention did not achieve the highest PSNR, it still offers excellent performance in preserving image details.
Table 1. Different Pix2Pix Model Performance in Image Denoising.
PSNR | SSIM | |
Pix2Pix | 36.78 | 0.9408 |
Pix2Pix-self-attention | 37.64 | 0.9524 |
Pix2Pix-residual block | 38.02 | 0.9588 |
Pix2pix+residual block+self attention | 37.7 | 0.9554 |

Figure 2. Denoising Results of Astronomical Images by Different Pix2Pix Model Variants.
In Figure 2, it is evident that various Pix2Pix model variants demonstrate commendable performance in denoising astronomical images, producing outputs that closely resemble the ground truth. However, an intriguing observation emerges from the analysis: despite the significant reduction in noise, the output images exhibit noticeably lower saturation compared to the target images. This phenomenon likely results from the models' tendency to overly suppress color intensity during the noise reduction process, potentially leading to a loss in detail and vibrancy of colors. This insight suggests a need for further refinement in the models to balance noise suppression with color preservation, ensuring that essential image qualities are not compromised in the quest for clarity.
5. Limitations and future trends
While the enhanced Pix2Pix model proposed in this study shows significant improvements in denoising tasks, there are still limitations that require further investigation. Although incorporating Residual Blocks and Self-Attention mechanisms enhances noise removal and detail preservation, these modifications can increase model complexity and computational demands. This poses a challenge for practical applications, especially when processing large-scale astronomical datasets, where computational efficiency remains a critical concern. Another limitation is the use of software-simulated noise to validate the model's effectiveness. While these simulated noises provide a controlled environment to test the model's capabilities, they may not fully represent the complexity of real-world noise encountered in astronomical observations. This discrepancy might explain the limited performance differences observed among the various models tested. Future research should incorporate real observational noise types, such as sensor noise, light pollution, and background noise, to better evaluate and enhance the model's robustness and applicability in real scenarios.
Additionally, although high-resolution image datasets were used in this study, future work could explore the application of this model to even higher resolutions or full-image scales to capture finer details in astronomical images. Achieving this will require further optimization of the model design and training strategies to handle larger inputs and more complex features effectively. Future research could also involve integrating this model with other advanced deep learning techniques, such as Transformer architectures, to further improve denoising performance and flexibility. Moreover, developing automated data preprocessing and augmentation techniques could enhance the model's generalization across different datasets and observational conditions.
Addressing these challenges and expanding the scope of research could make the enhanced Pix2Pix model a more effective and versatile solution for astronomical image denoising, providing clearer and more reliable images for scientific analysis.
6. Conclusion
This study presents an enhanced Pix2Pix model specifically designed for denoising astronomical images affected by sensor noise. By incorporating Residual Blocks and Self-Attention mechanisms, the model demonstrated significant improvements in noise reduction and detail preservation. Compared to traditional denoising methods and other Pix2Pix variants, this enhanced model achieved superior performance in terms of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM), especially in scenarios where maintaining image details is crucial. The use of Residual Blocks effectively mitigated the vanishing gradient problem in deep networks and helped retain high-frequency information. The Self-Attention mechanism improved the model's ability to capture global context, making it more effective at distinguishing noise from meaningful structures. Experimental results confirmed that these enhancements contribute to the model's robustness and accuracy in denoising tasks.
However, there are limitations to this study, including increased computational complexity and reliance on simulated noise. Future research should focus on incorporating real observational noise to validate the model’s effectiveness in practical applications. Additionally, further optimization of the model architecture and training strategies is needed to handle larger datasets and higher resolution images. Exploring the integration of other deep learning techniques, such as Transformer architectures, could also enhance the denoising performance and flexibility of the model.
In conclusion, this enhanced Pix2Pix model offers an effective solution for denoising astronomical images, providing clearer and more accurate data for scientific analysis. The study highlights the potential of advanced deep learning techniques in addressing the challenges posed by sensor noise, paving the way for more precise astronomical observations.
References
[1]. Kastner, J. H. 1998. Imaging science in astronomy. Pattern Recognition, pp. 172-174.
[2]. Misra, D., Mishra, S., and Appasani, B. 2018. Advanced Image Processing for Astronomical Images. arXiv preprint arXiv:1812.09702. DOI: https://doi.org/10.48550/arXiv.1812.09702
[3]. Zhu, H.J., Han, B.C., and Qiu, B. 2015. Survey of Astronomical Image Processing Methods. In Zhang, Y.J. (ed) Image and Graphics. Lecture Notes in Computer Science, vol. 9219. Springer, Cham. DOI: https://doi.org/10.1007/978-3-319-21969-1_37
[4]. Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. 2016. Image-to-Image Translation with Conditional Adversarial Networks. arXiv preprint arXiv:1611.07004. DOI: https://doi.org/10.48550/arXiv.1611.07004
[5]. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. 2014. Generative Adversarial Networks. arXiv preprint arXiv:1406.2661. DOI: https://doi.org/10.48550/arXiv.1406.2661
[6]. He, K., Zhang, X., Ren, S., and Sun, J. 2015. Deep Residual Learning for Image Recognition. arXiv preprint arXiv:1512.03385. DOI: https://doi.org/10.48550/arXiv.1512.03385
[7]. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. 2017. Attention Is All You Need. arXiv preprint arXiv:1706.03762. DOI: https://doi.org/10.48550/arXiv.1706.03762
[8]. Wang, X., Girshick, R., Gupta, A., and He, K. 2018. Non-local Neural Networks. arXiv preprint arXiv:1711.07971. DOI: https://doi.org/10.48550/arXiv.1711.07971
[9]. Gonzalez, R. C., and Woods, R. E. 2008. Digital Image Processing. 3rd ed. Prentice-Hall, Inc., Upper Saddle River, NJ, USA.
[10]. Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 4 (April 2004), 600-612. DOI: https://doi.org/10.1109/TIP.2003.819861
[11]. Singh, G., Mittal, A., and Aggarwal, N. 2020. ResDNN: Deep Residual Learning for Natural Image Denoising. IET Image Processing, 14, 11 (Sep. 2020), 2425–2434. DOI: https://doi.org/10.1049/iet-ipr.2019.0623
[12]. Li, M., Hsu, W., Xie, X., Cong, J., and Gao, W. 2020. SACNN: Self-Attention Convolutional Neural Network for Low-Dose CT Denoising With Self-Supervised Perceptual Loss Network. IEEE Transactions on Medical Imaging, 39, no. 7, pp. 2289-2301. DOI: 10.1109/TMI.2020.2968472
[13]. Zuo, Z., Chen, X., Xu, H., Li, J., Liao, W., Yang, Z-X., and Wang, S. 2022. IDEA-Net: Adaptive Dual Self-Attention Network for Single Image Denoising. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) Workshops, pp. 739-748.
[14]. Shen, L.-C., Liu, Y., Song, J., and Yu, D.-J. 2021. SAResNet: Self-Attention Residual Network for Predicting DNA-Protein Binding. Briefings in Bioinformatics, 22, Issue 5, September 2021, bbab101. DOI: https://doi.org/10.1093/bib/bbab101
[15]. Zhang, H., Lian, Q., Zhao, J., Wang, Y., Yang, Y., and Feng, S. 2022. RatUNet: Residual U-Net Based on Attention Mechanism for Image Denoising. PeerJ Computer Science, 8 DOI: https://doi.org/10.7717/peerj-cs.970
[16]. ESA Webb. ESA Official TIF Astronomical Images. Available at: https://esawebb.org/images/
[17]. Aladdin Persson. Machine Learning Collection. Available at: https://github.com/aladdinpersson/Machine-Learning-Collection
[18]. Gotmare, A., Keskar, N. S., Xiong, C., and Socher, R. 2018. A Closer Look at Deep Learning Heuristics: Learning Rate Restarts, Warmup and Distillation. arXiv preprint arXiv:1810.13243.
[19]. Zhang, J., He, T., Sra, S., and Jadbabaie, A. 2019. Why Gradient Clipping Accelerates Training: A Theoretical Justification for Adaptivity. arXiv preprint arXiv:1905.11881.
[20]. Daubechies, I., DeVore, R., Foucart, S., Hanin, B., and Petrova, G. 2022. Nonlinear Approximation and (Deep) ReLU Networks. Constructive Approximation, 55(1), pp. 127-172.
[21]. Xu, J., Li, Z., Du, B., Zhang, M., and Liu, J. 2020. Reluplex Made More Practical: Leaky ReLU. In 2020 IEEE Symposium on Computers and Communications (ISCC), pp. 1-7.
[22]. Xu, J., Sun, X., Zhang, Z., Zhao, G., and Lin, J. 2019. Understanding and Improving Layer Normalization. Advances in Neural Information Processing Systems, 32.
[23]. Nam, H., and Kim, H. E. 2018. Batch-Instance Normalization for Adaptively Style-Invariant Neural Networks. Advances in Neural Information Processing Systems, 31.
[24]. Apicella, A., Donnarumma, F., Isgrò, F., and Prevete, R. 2021. A Survey on Modern Trainable Activation Functions. Neural Networks, 138, pp. 14-32.
[25]. Kalman, B. L., and Kwasny, S. C. 1992. Why tanh: Choosing a Sigmoidal Function. In Proceedings 1992 IJCNN International Joint Conference on Neural Networks, Vol. 4, pp. 578-581.
Cite this article
Xu,M. (2024). Denoising astronomical images using an enhanced Pix2Pix model. Applied and Computational Engineering,88,253-260.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 6th International Conference on Computing and Data Science
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Kastner, J. H. 1998. Imaging science in astronomy. Pattern Recognition, pp. 172-174.
[2]. Misra, D., Mishra, S., and Appasani, B. 2018. Advanced Image Processing for Astronomical Images. arXiv preprint arXiv:1812.09702. DOI: https://doi.org/10.48550/arXiv.1812.09702
[3]. Zhu, H.J., Han, B.C., and Qiu, B. 2015. Survey of Astronomical Image Processing Methods. In Zhang, Y.J. (ed) Image and Graphics. Lecture Notes in Computer Science, vol. 9219. Springer, Cham. DOI: https://doi.org/10.1007/978-3-319-21969-1_37
[4]. Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. 2016. Image-to-Image Translation with Conditional Adversarial Networks. arXiv preprint arXiv:1611.07004. DOI: https://doi.org/10.48550/arXiv.1611.07004
[5]. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. 2014. Generative Adversarial Networks. arXiv preprint arXiv:1406.2661. DOI: https://doi.org/10.48550/arXiv.1406.2661
[6]. He, K., Zhang, X., Ren, S., and Sun, J. 2015. Deep Residual Learning for Image Recognition. arXiv preprint arXiv:1512.03385. DOI: https://doi.org/10.48550/arXiv.1512.03385
[7]. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. 2017. Attention Is All You Need. arXiv preprint arXiv:1706.03762. DOI: https://doi.org/10.48550/arXiv.1706.03762
[8]. Wang, X., Girshick, R., Gupta, A., and He, K. 2018. Non-local Neural Networks. arXiv preprint arXiv:1711.07971. DOI: https://doi.org/10.48550/arXiv.1711.07971
[9]. Gonzalez, R. C., and Woods, R. E. 2008. Digital Image Processing. 3rd ed. Prentice-Hall, Inc., Upper Saddle River, NJ, USA.
[10]. Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. 2004. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 4 (April 2004), 600-612. DOI: https://doi.org/10.1109/TIP.2003.819861
[11]. Singh, G., Mittal, A., and Aggarwal, N. 2020. ResDNN: Deep Residual Learning for Natural Image Denoising. IET Image Processing, 14, 11 (Sep. 2020), 2425–2434. DOI: https://doi.org/10.1049/iet-ipr.2019.0623
[12]. Li, M., Hsu, W., Xie, X., Cong, J., and Gao, W. 2020. SACNN: Self-Attention Convolutional Neural Network for Low-Dose CT Denoising With Self-Supervised Perceptual Loss Network. IEEE Transactions on Medical Imaging, 39, no. 7, pp. 2289-2301. DOI: 10.1109/TMI.2020.2968472
[13]. Zuo, Z., Chen, X., Xu, H., Li, J., Liao, W., Yang, Z-X., and Wang, S. 2022. IDEA-Net: Adaptive Dual Self-Attention Network for Single Image Denoising. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) Workshops, pp. 739-748.
[14]. Shen, L.-C., Liu, Y., Song, J., and Yu, D.-J. 2021. SAResNet: Self-Attention Residual Network for Predicting DNA-Protein Binding. Briefings in Bioinformatics, 22, Issue 5, September 2021, bbab101. DOI: https://doi.org/10.1093/bib/bbab101
[15]. Zhang, H., Lian, Q., Zhao, J., Wang, Y., Yang, Y., and Feng, S. 2022. RatUNet: Residual U-Net Based on Attention Mechanism for Image Denoising. PeerJ Computer Science, 8 DOI: https://doi.org/10.7717/peerj-cs.970
[16]. ESA Webb. ESA Official TIF Astronomical Images. Available at: https://esawebb.org/images/
[17]. Aladdin Persson. Machine Learning Collection. Available at: https://github.com/aladdinpersson/Machine-Learning-Collection
[18]. Gotmare, A., Keskar, N. S., Xiong, C., and Socher, R. 2018. A Closer Look at Deep Learning Heuristics: Learning Rate Restarts, Warmup and Distillation. arXiv preprint arXiv:1810.13243.
[19]. Zhang, J., He, T., Sra, S., and Jadbabaie, A. 2019. Why Gradient Clipping Accelerates Training: A Theoretical Justification for Adaptivity. arXiv preprint arXiv:1905.11881.
[20]. Daubechies, I., DeVore, R., Foucart, S., Hanin, B., and Petrova, G. 2022. Nonlinear Approximation and (Deep) ReLU Networks. Constructive Approximation, 55(1), pp. 127-172.
[21]. Xu, J., Li, Z., Du, B., Zhang, M., and Liu, J. 2020. Reluplex Made More Practical: Leaky ReLU. In 2020 IEEE Symposium on Computers and Communications (ISCC), pp. 1-7.
[22]. Xu, J., Sun, X., Zhang, Z., Zhao, G., and Lin, J. 2019. Understanding and Improving Layer Normalization. Advances in Neural Information Processing Systems, 32.
[23]. Nam, H., and Kim, H. E. 2018. Batch-Instance Normalization for Adaptively Style-Invariant Neural Networks. Advances in Neural Information Processing Systems, 31.
[24]. Apicella, A., Donnarumma, F., Isgrò, F., and Prevete, R. 2021. A Survey on Modern Trainable Activation Functions. Neural Networks, 138, pp. 14-32.
[25]. Kalman, B. L., and Kwasny, S. C. 1992. Why tanh: Choosing a Sigmoidal Function. In Proceedings 1992 IJCNN International Joint Conference on Neural Networks, Vol. 4, pp. 578-581.









