1 Introduction

Traditional scheduling problems in hybrid flow assembly workshops are mainly divided into two phases: matching operations with machines and determining the sequence of operations. The first phase of the hybrid flow shop model studied in this article involves batching the assembly tasks, i.e., determining the specific quantity of each product per batch. The second phase involves selecting parallel machines, where machines in real production can operate at different speeds during assembly. This phase aims to optimize workshop scheduling by considering the operating speed of parallel machines, associated energy consumption, idle energy consumption of machines, energy consumption of different operations, and the energy and time costs of switching between different operations on different machines. The third phase determines the sequence of operations on each machine. Considering the different preparation times for switching between operations on parallel machines, this phase explores the optimal assembly schedule. The three-phase scheduling problem flow model for the hybrid flow assembly workshop studied in this article is shown in Figure 1.

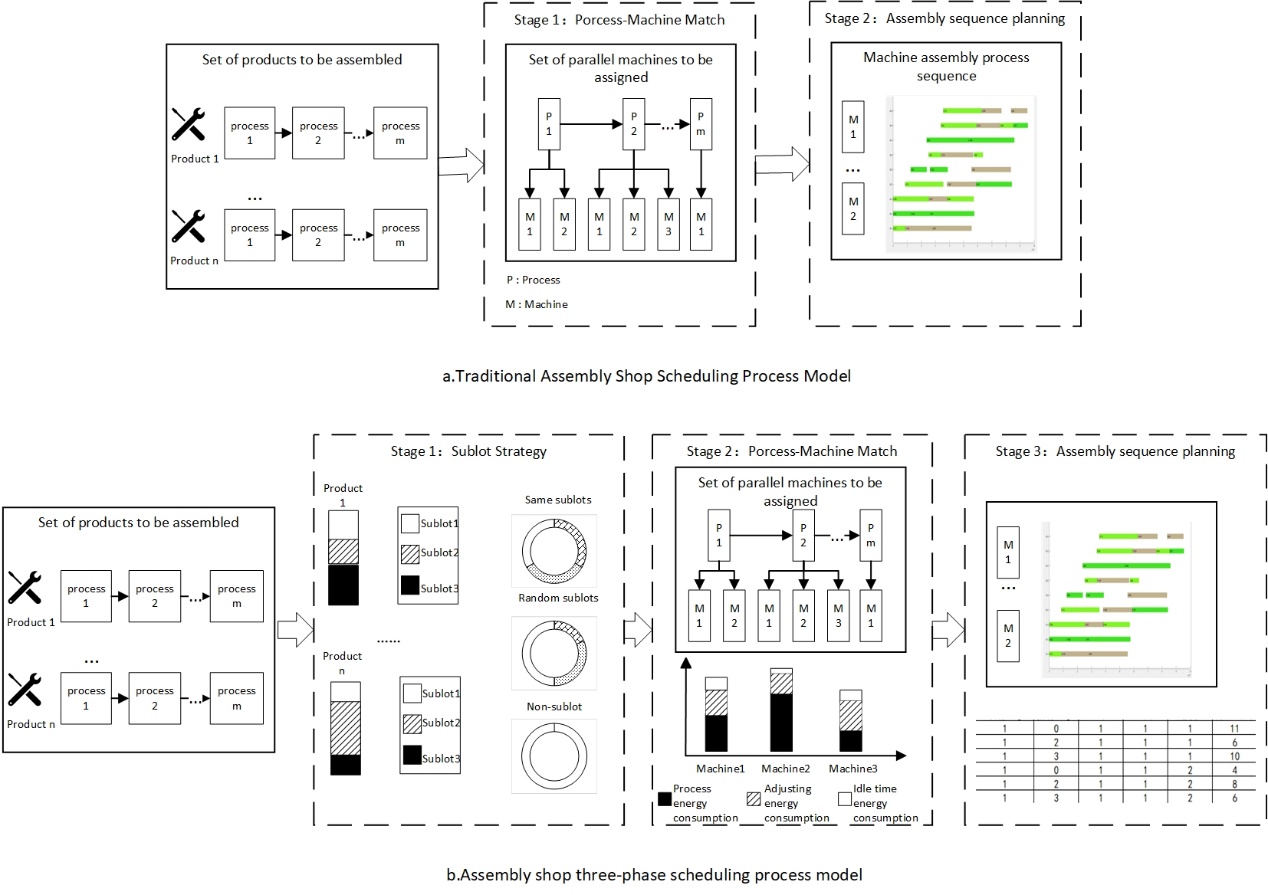
Figure 1 The three-phase scheduling problem flow model for the hybrid flow assembly workshop

2 Literature Review

In real-world applications, the problem of scheduling hybrid flow shops is prevalent in industries such as automobile manufacturing, aerospace component assembly, and complex military product assembly. Hybrid flow shops introduce parallel heterospeed machines to the traditional flow shop setting, complicating the constraints faced in solving these scheduling problems, which are considered NP-Hard. Addressing these challenges can significantly enhance a company's production efficiency, reduce energy consumption and production costs, thus boosting its competitiveness.

Different production environments have diverse requirements for scheduling objectives. Hybrid flow shop scheduling optimization goals can be categorized into single-objective and multi-objective optimization problems. Currently, research on solving multi-objective optimization problems using intelligent algorithms is abundant and can be broadly divided into four categories:

Population-based intelligent algorithms: Yankai W et al. [1] analyzed constraints in the actual operation of hot rolling workshops and designed an improved whale algorithm that considers time and energy parameters. These population-based algorithms, primarily inspired by animal behavior, excel at generating a large number of feasible solutions. Current research mainly focuses on how to better select the next generation of populations to achieve superior solutions.

Intelligent algorithms based on human behavior learning: Song C et al. [2] introduced a hybrid teaching optimization algorithm supporting five decoding rules to reduce workshop energy consumption without altering the total completion time. Algorithms based on human behavior typically involve mutual learning among individuals, with current research emphasizing how to achieve higher learning efficiency and better outcomes among individuals.

Evolutionary intelligent algorithms: Liu Z et al. [3] addressed complex relationships between heating furnaces and other equipment in forging production by proposing a model that minimizes manufacturing time and energy consumption. This model establishes new rules for identifying optimal transportation sequences and timings using evolutionary algorithms. Han W et al. [4] incorporated the impact of operators into the constraints and proposed a multi-objective evolutionary algorithm that combines four rules for assigning machine and worker priorities, and introduced the earliest deadline rule to further enhance the algorithm's performance.

Hybrid algorithms: Schulz S et al. [5] demonstrated the importance of energy-aware scheduling in operational management and proposed a new multi-stage iterative local search algorithm to compute a three-dimensional Pareto frontier involving completion time, workshop energy consumption, and peak load. Zhang B et al. [6] considered different energy consumption ratios, sequence-dependent setup, and inter-machine transport operations to propose a decomposition-based three-stage multi-objective method to solve the problem. Fu Y et al. [7] proposed an adaptive multi-population parallel genetic algorithm considering multiple time parameters, improving the algorithm's efficiency by allowing multiple populations to search in parallel within multiple intervals.

3 Multi-objective Energy-efficient Scheduling Algorithm

In real manufacturing scenarios, machines used differ in their power consumption rates and completion times. Typically, faster completions incur higher energy costs, creating a trade-off relationship. Thus, addressing this issue in multi-objective hybrid flow shop batch energy-efficient scheduling is crucial. The problem considers minimizing the maximum completion time and the energy consumption in assembly workshops as a multi-objective issue, with completion time and power consumption inversely related. Reducing completion time necessitates increased energy expenditure, and vice versa. Machine speed is key to determining the exact relationship between maximum completion time and energy usage, implying that controlling the speed of each machine can adjust the relationship between maximum completion time and power consumption. To tackle this multi-objective problem, the following variables are defined:

3.1 Variable Definitions

To establish a mathematical model for the described problem, the following variables are defined. Table 1 provides parameters needed for model construction, describing the actual production environment of the assembly workshop. It includes the process routes of products, machines' available start times, two temporal characteristics of machines (processing time, inter-operation adjustment time), three energy characteristics of machines (processing energy consumption, inter-operation adjustment energy consumption, idle energy consumption), and the quantity contained in each sub-batch of products.

Table 1 Model Parameters

3.2 Objective Functions and Constraints

\( Minimize F1 = c_{max} \)

\( Minimize F2 = p_{max} \)

\( c_{max}≥ct_{j,n,i} \)

\( p_{max}≥\sum_{}^{} (PW_{m,i,s}×v_{r,m,i,j,n,s}×λ_{j,n}×T_{n,m,i,s})+\sum_{}^{} (SW_{m,i,s}×v_{r,m,i,j,n,s}×ST_{m,i,n,p,s}) \)

\( +\sum_{}^{} PI_{m,i}×[c_{max}-\sum_{}^{} v_{r,m,i,j,n,s}×(λ_{j,n}×T_{n,m,i,s}+ST_{m,i,n,p,s})] \)

\( st_{j,n,i}≥st_{j,n,i-1}+λ_{j,n}×T_{n,m,i,s}+λ_{j,n}×ST_{m,i,n,p,s} \)

\( \hat{t}_{1,m,i}-v_{1,m,i,j,n,s}×(λ_{j,n}×T_{n,m,i,s}+ST_{m,i,n,0,s})-θ×x_{1,m,i,j,n}+θ≥MC_{m,i} \)

\( \hat{t}_{r,m,i}-\sum_{}^{} v_{r,m,i,j,n,s}×(λ_{j,n}×T_{n,m,i,s}+ST_{m,i,n,p,s}) \)

\( -θ(y_{r-1,m,i,p}+x_{r,m,i,j,n})+2θ≥\hat{c}_{r-1,m,i} \)

Equation (1) represents the objective constraint of minimizing the maximum completion time, while Equation (2) aims to minimize the workshop's energy consumption. Equation (3) imposes the completion time constraint, ensuring that the completion time of any sub-batch in the scheduling plan is greater than or equal to its actual completion time. Equation (4) sets the workshop's energy consumption constraint, where the total energy consumption of the workshop must be greater than or equal to the sum of processing energy, adjustment energy, and idle energy of all machines in the scheduling plan. Equation (5) ensures that the start time of the succeeding operation of the same sub-batch is later than the completion time of the previous operation plus the adjustment time between the two operations. Equation (6) stipulates that the start time of the first operation of a machine executing operation i must be after the completion time of the first adjustment of the machine executing operation i (assuming the first operation on this machine is processing the jth sub-batch of the product). Equation (7) calculates the start time of machine adjustment during its rth run, excluding adjustment time if the adjacent runs on the same machine process the same product's same operation. To effectively reduce the overall completion time, preparation for the next sub-batch of a product can start before the assembly of the preceding sub-batch is completed, directly reducing the overall assembly time after adjustment completion.

3.3 Algorithm Design

In solving the aforementioned problem, this paper designs a multi-objective hybrid flow shop batch energy-efficient scheduling algorithm based on the improved non-dominated sorting genetic algorithm II (NSGA-II) with an elite reserve strategy (MO-HFSP-Batch). Figure 2 details the algorithm flow designed in this section. To address the problem of uneven spatial distribution of populations caused by random initialization and high uncertainty, a population strategy based on the initialization of excellent points is introduced. After crossover and mutation operations based on the process of non-dominated sorting genetic algorithm, non-dominated sorting and crowding distance calculation are performed. Subsequently, a hybrid selection strategy based on roulette selection and elite retention is designed to select the population, improving the algorithm's optimization capability through multiple iterations to generate satisfactory Pareto optimal solutions successively.

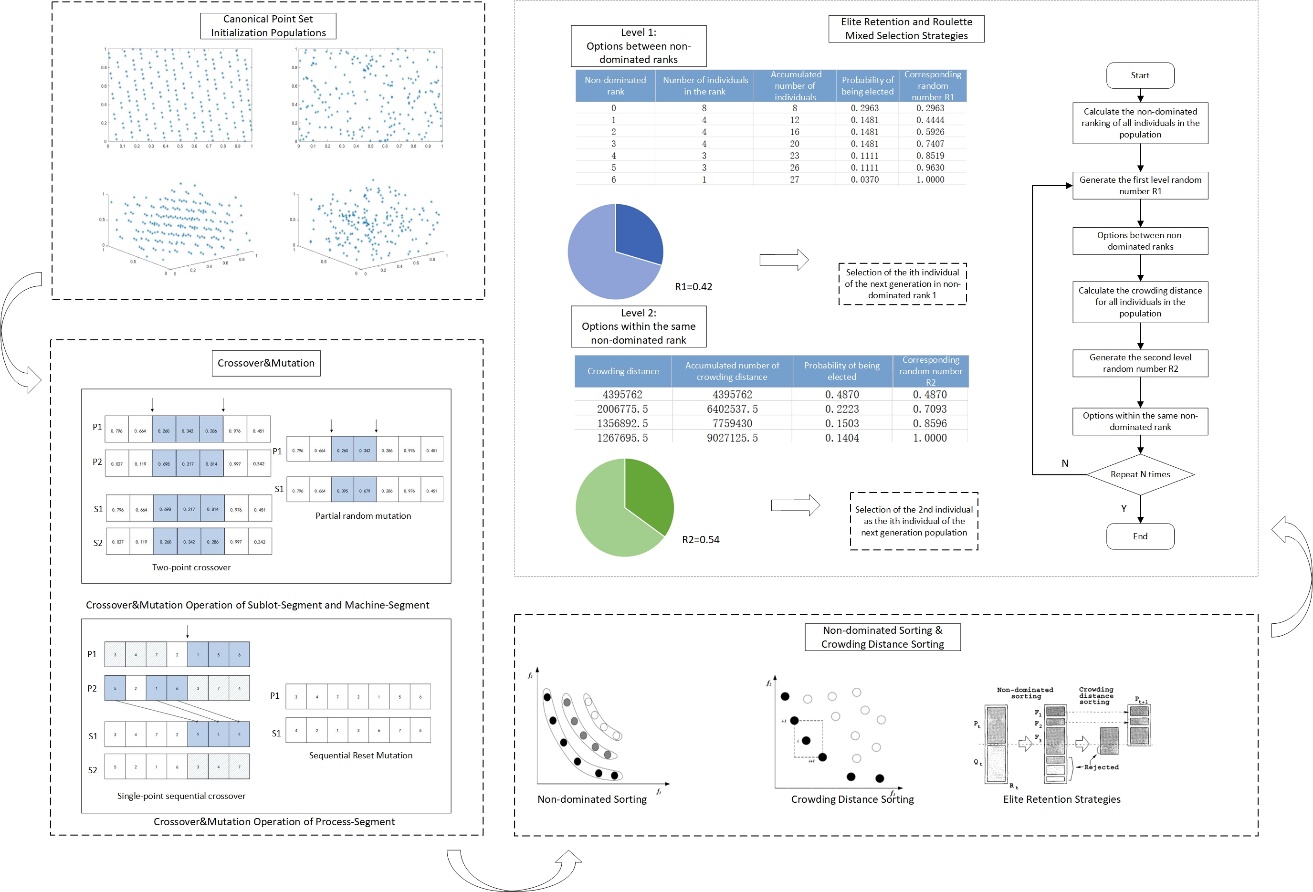
Figure 2 MO-HFSP-Batch Algorithm Flowchart

In this scheduling, there are three major decision stages: selection of assembly task sub-batches, selection of parallel machines for each operation, and scheduling of assembly operations. Therefore, a three-layer chromosome encoding is designed to solve the above three types of selections. The chromosome is divided into three segments: the left part (Sublot-Segment) is encoded with random numbers, representing the size of each batch of sub-lots for each operation, denoted as \( α_{j,n} \) , taking values in the range [0,1], with a coding length equal to the sum of all sub-lots of all products. The middle part (Machine-Segment) is encoded with random numbers, representing the speed levels and machine codes, denoted as \( β_{j,n,i} \) , taking values in the range [0,1], with a coding length equal to the product of the sum of all sub-lots of all products and the maximum number of operations required for products. The right part (Process-Segment) is encoded with integers, representing the sequence of the first operation assigned to each sub-batch, with a coding length equal to the sum of all sub-batches of all products. The sub-lot number on the left corresponds to the position of the right part, indicating the order in which the first operation of each sub-batch is assigned to a machine. The specific parallel machine selection follows the model constraints, considering the available start time for each parallel machine. The specific decoding method is illustrated in Figure 3.

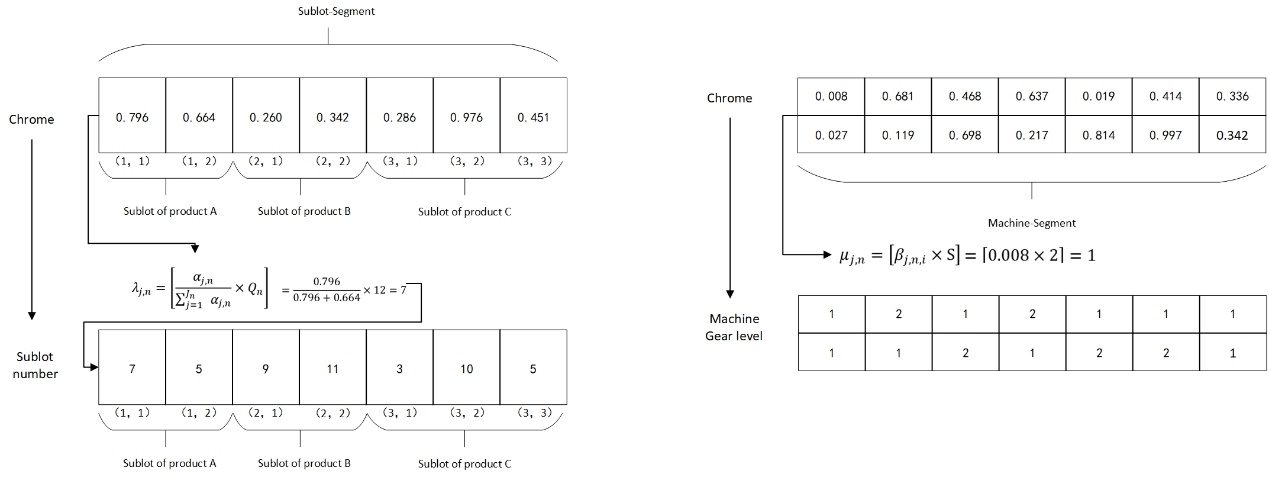
Figure 3 Chromosome Decoding Method

For the left and middle parts encoded with random numbers, two-point crossover and partial random mutation are employed. For the right part encoded with integers, single-point sequence crossover is adopted to ensure the executable nature of chromosomes after crossover and mutation operations. During mutation operations, a sequence reset mutation strategy is used to maintain the chromosome's executability. This mutation method helps increase population diversity and enhance the search capability of the genetic algorithm.

4 Experiment Analysis

This paper conducts a comparative analysis on the completion time, workshop energy consumption, and stability of the Pareto solution set using four different algorithms for four test sets of the energy-optimized hybrid flow shop. The algorithms compared are the MO-HFSP-Batch algorithm proposed in this paper, the NSGA-II algorithm, the Teaching-Learning-Based Optimization (TLBO) algorithm, and the improved TLBO (TLBO-Ch) using the method developed in this paper. By applying these four algorithms to the datasets and solving for completion time and workshop energy consumption, the data output reflects the ability of the algorithms to address these two objectives to some extent. The comparison of the Pareto fronts for each dataset, as shown in Figure 4, effectively illustrates the quantity and distribution of the non-dominated solutions.

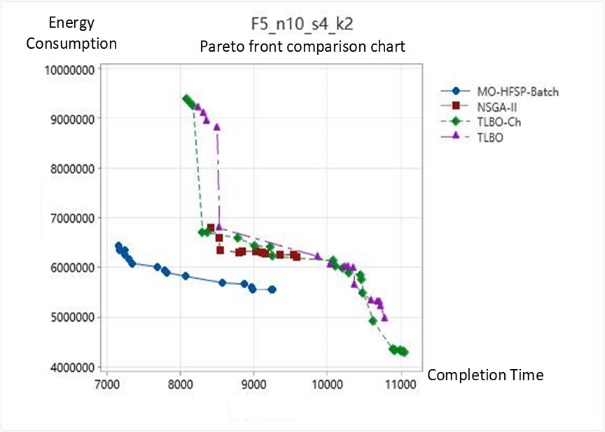
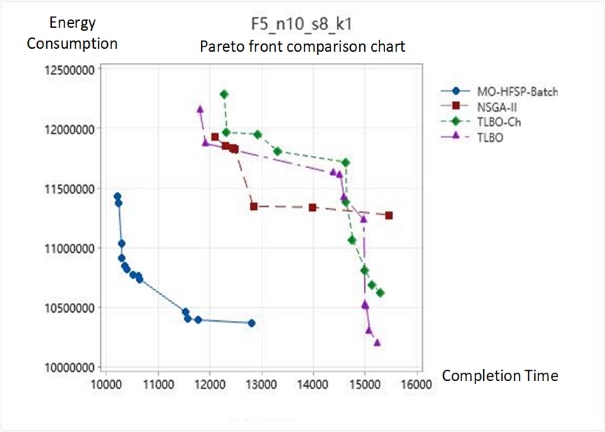
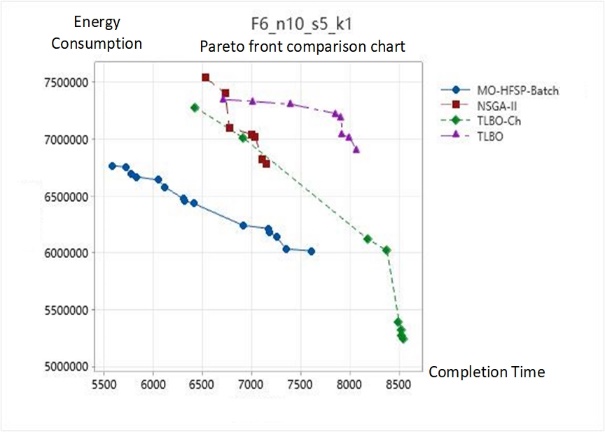
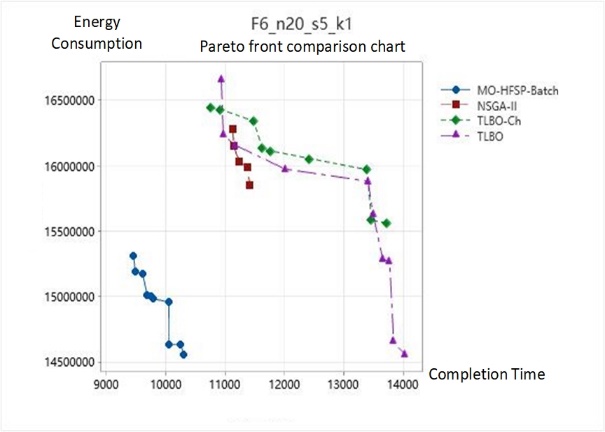
Figure 4 Comparison of Pareto Fronts for Dataset Solutions by the Four Algorithms

5 Conclusion

After analyzing the operational mode of the hybrid flow shop and identifying two critical indicators reflecting the level of workshop management, this paper establishes a multi-objective optimization model for hybrid flow shops aimed at minimizing the maximum completion time and minimizing energy consumption in the workshop. To meet the practical assembly needs of the workshop, batch flow assembly for components and consideration of idle and adjustment energy consumption for machinery were integrated into the operational considerations. To solve the aforementioned problems, the MO-HFSP-Batch algorithm based on an improved NSGA-II is proposed, which optimizes the initial and iterative population selection processes and features a three-layer chromosome structure that accounts for batches, parallel machines, and operation sequences. Extensive empirical data demonstrates that this algorithm can effectively optimize both objectives, particularly offering stable optimization in terms of completion time. Additionally, the distribution of the non-dominated solution set obtained by the algorithm is quite stable and more aligned with actual hybrid flow shop assembly scenarios, where there is no significant preference for either objective. The algorithm consistently outperforms others in terms of the average completion time; in test datasets, it can reduce processing time by up to 30.2% and reduce workshop energy consumption by up to 28.9%. Furthermore, the standard deviation of both indicators is also more stable when compared to other algorithms. By combining the comparison of Pareto fronts, it is evident that the scheduling plans generated by this algorithm show a nearly equal preference for the two objectives to optimize, resulting in outcomes that are within a more stable range. In scenarios where workshop decision-makers do not have a clear preference for either objective, this algorithm can output effective and stable scheduling decisions.