1. Introduction

Depth estimation is a crucial part in the field of computer vision, with extensive applications in navigation tasks. The ability to accurately perceive and interpret the three-dimensional structure of the environment from a two-dimensional image is vital for machines to interact correctly and efficiently in real life.

Historically, depth estimation has been approached through a variety of methods. Traditional techniques, like stereo vision, rely on multiple cameras to mimic human binocular vision, inferring depth from the disparity between two images captured from slightly different viewpoints. Other methods include structured-light systems that project a pattern onto the scene and measure deformations of this pattern to deduce depth. However, such methods often require specific hardware setups and controlled lighting conditions, limiting their applicability in dynamic environments.

The advent of deep learning has revolutionized this domain, with convolutional neural networks (CNNs) setting new benchmarks in accuracy and robustness. Early machine learning approaches involved feature extraction and regression techniques. Later, models such as AlexNet [1] and subsequent architectures like VGG [2] and ResNet [3] also pushed the boundaries by enabling feature learning directly from data, eliminating the need for manual feature design and greatly improving the accuracy and efficiency of the model. Recent researchers have put forward more advanced architectures such as UNet [4] and FCN [5] for pixel-level predictions, allowing for detailed depth maps from single images. Innovations in network design, such as DenseNet [6] and the introduction of attention mechanisms [7], have further refined the accuracy of depth predictions under various conditions. However, these deep learning-based methods often struggle with generalization. Furthermore, the computational efficiency of deep learning models and their ability to operate in real-time on edge devices remain a concern, particularly for applications in mobile robotics and navigation systems.

This paper proposes a hybrid network model, which is a novel approach that combines the strengths of ResNet and UNet architectures for robust feature extraction and depth map reconstruction [8]. Furthermore, it innovatively incorporates a SoftHebbLayer, inspired by Hebbian learning principles through dynamic feature weighting, enhancing the adaptability of the network. This layer allows the network to self-adjust and improve based on individual learning principles instead of only backpropagation (bp) algorithm, which states that the efficiency of neurons increases when they are simultaneously activated, thus strengthening their connection. By integrating these elements, our model aims to not only tackle the traditional challenges of depth estimation but also to improve the learning process, making it more suited for diverse and dynamic environments encountered in real-world scenarios. While keeping a good performance at the same time, this model greatly improves the efficiency of computational resources, making it a lighter and more convenient model in applications. The broad applications of this technology range from improving the operational efficiency of autonomous vehicles in unstructured environments to enhancing interactive user experiences in augmented and virtual reality. Looking forward, the model’s potential for adaptation and efficiency opens new avenues for research, particularly in optimizing architecture for even broader application scenarios and further reducing the computational demands for complex depth estimation tasks. As the technology matures, integrating multi-model sensory inputs—combining visual data with radar, LIDAR, and other sensor inputs—could enhance depth estimation accuracy and reliability, paving the way for more intelligent and autonomous systems capable of operating in diverse conditions and environments.

2. Method

In this section, we will discuss the relevant method for training a navigation neural network using visual inputs, random movements, and the mechanism of grid cells and Hebbian learning. There are several key elements in the system: a CNN for processing visual inputs, a movement with random noise for simulating the real-world conditions, and a learning mechanism inspired by Hebbian learning. The principal goal of the system is to teach the model how to find the desired vector towards the target based on visual inputs, while also handling noise and uncertainty as animals do in real life.

2.1. Visual Input and CNN Processing

2.1.1. Visual Input

The system receives visual inputs in the form of images captured at different positions both indoors and outdoors during the navigation. Each input image corresponds to the current view of the agent. All these images are pre-processed (resized rotated and normalized) before being fed into the CNN for feature extraction. The input images should have a consistent view and resolution, representing the fixed field of vision in mammals’ eyes.

2.1.2. CNN Architecture

To better process visual inputs and effectively extract meaningful features from the images, we employ a mixed CNN architecture that combines UNet and ResNet structures. This structure helps us to segment the image, find the target, and finally handle complex spatial information and greatly improve the accuracy of the navigation neural network.

At the core of the encoder module, ResNet’s proven architecture, specifically the ResNet-34 variant, is employed for its efficiency and effectiveness in feature extraction. The ResNet backbone is modified to suit depth estimation tasks by adapting its final layers to produce feature maps that retain more spatial information, which is essential for subsequent depth decoding process. The decoder module of the model utilizes a UNet architecture, which excels in precise localization needed for detailed depth map reconstruction. The decoder consists of a series of upsampling layers that refine these features to recover fine details lost during the downsampling in the encoder.

2.1.3. Evaluation Criterion

The choice of loss function significantly impacts the performance of deep learning models, especially in tasks like depth estimation where precision is critical. Traditional loss functions such as Mean Squared Error (MSE) and Mean Absolute Error (MAE) are commonly used due to their straightforwardness and effectiveness in penalizing prediction errors. However, these loss functions have limitations that can affect the model’s ability to accurately predict depth maps in more complex scenarios.

While MSE is excellent for large errors due to its squaring of residuals, it can lead to the model disproportionately focusing on larger errors, sometimes at the expense of overall accuracy. This can result in models that perform well on average but miss finer details in depth maps. MAE provides a linear evaluation of errors, which makes it robust against outliers to some extent. However, its linear nature might not adequately penalize larger errors, which are more detrimental in depth estimation tasks, potentially leading to underfitting in scenarios with significant depth differences.

Instead of using MSE or MAE directly, we choose to use Huber Loss, which combines elements of both MSE and MAE, bring the best of both criteria in terms of sensitivity and robustness.

\[ L_\delta\leq ft(y,\widetilde{y}\right)=\begin{cases}\frac{1}{2}(y - \widetilde{y})^{2}, *(y - \widetilde{y}*)≤δ \\ δ*(y - \widetilde{y}*) - \frac{1}{2}δ^{2}, *(y - \widetilde{y}*)\text{>}δ\end{cases}\Biggl \] (1)

In our model, the threshold is 20% of the largest error in the batch. By introducing this dynamic threshold, the loss function can adapt to the range of errors in each training step, ensuring that the loss calculation remains sensitive to smaller errors while controlling the impact of larger errors.

2.2. Hebbian Learning Mechanism

The connection between CNN outputs and final results is updated using the Hebbian Learning Rule with the SoftHebbLayer [9]. In biology, the Hebbian rule is often summarized as “cells that fire together, wire together.” If two neurons are activated concurrently, the connection between them strengthens [10]. In this model, the update rule is given by:

\( \mathrm{\Delta}\omega_{ij}=\eta\cdot x_i\cdot y_j\Biggl \) (2)

Where \( \omega_{ij} \) is the weight between the i-th input neuron and the j-th grid cell, \( x_i \) and \( y_j \) are binary variables (value is 1 when active, value is 0 when inactive), and \( \eta \) is the learning rate (1e-5). Through the Hebbian Learning Mechanism, the network can better adjust the connection between CNN-extracted features and the spatial information in the final results, allowing the model to improve its performance in navigation tasks.

2.3. Training and Optimization

There are two major training processes involved in the model. The first process involves backpropagation (bp) and gradient descent [11] in CNN, making it possible to update weights and better extract features from the input images. Another process is the Hebbian Learning Mechanism layer. This process helps adjust the connections between CNN’s decoders based on their co-activation.

3. Results

3.1. Dataset

The results of the experiment strongly demonstrated the effectiveness of the proposed UNet + ResNet combined with Hebbian Learning Mechanism for solving navigation tasks. The model was trained on the DIODE dataset [12], which contains diverse high-resolution color images with accurate, dense, far-range depth measurements. In the dataset, there are both indoor and outdoor scenes with RGBD pairs, as illustrated in figure 1 showing example RGBD pairs from the dataset. This variety allows the network to generalize well across the environment.

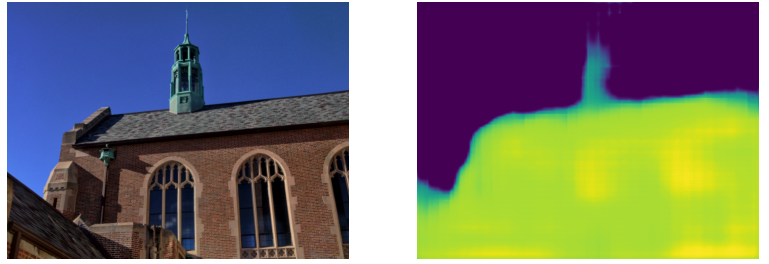
(a) Orginal image (b) Predicted depth map

Figure 1. DIODE Sample.

3.2. Evaluation Metrics

The model’s performance was evaluated using several metrics, including MSE, RMSE, Absolute Relative Error (ARE), and Log10 error. The results are summarized in following points:

The model achieved a MSE of 0.0800 on the validation set, showing its great ability to minimize prediction errors between the generated outputs and the ground truth. Such result shows that there are no larger errors as MSE is sensitive to outliers. The final model has a RMSE of 0.2805, providing an estimate of how far, on average, the predictions are from the ground truth. Although also sensitive to outliers, RMSE has the same units as the original values, making it easier to interpret. Log10 error focuses on the order of magnitude differences between predictions and actual values. In our model, the error is 0.5519, suggesting a small relative difference in the depth estimation.

4. Discussion

The results showed that the proposed hybrid network of UNet and ResNet, augmented with Hebbian learning mechanism, offers great advantages in solving complex visual tasks.

4.1. The Role of Hebbian Learning

One of the most important features of this project is the integration of Hebbian learning, which adjusts the weights between CNN layers based on co-activation. This biologically inspired mechanism enabled the model to better handle spatial features from the images. The Hebbian update rule, which strengthens connections between co-active neurons, allowed the network to refine its predictions over time, improving overall performance in complex environments.

4.2. Hybrid Network Architecture

The use of a hybrid network combining UNet and ResNet allowed the model to extract hierarchical features while preserving both local and global spatial information from the image. With the encoder-decoder structure, where the network decoder gradually reduces the spatial dimensions and the decoder restores spatial dimensions to make pixel-wise predictions, the features are effectively extracted. Also, the skip connections in the hybrid network architecture allow for training much deeper networks by addressing the vanishing gradient problem, making it possible for such a deep network to learn more complex features. By integrating ResNet as the backbone of the UNet encoder, the model’s ability of convergence is greatly improved.

4.3. Limitations and Future Improvements

Despite the promising results, there are still plenty of areas for improvement. Firstly, the current model is computationally expensive due to its complex architecture, particularly when dealing with high resolution images. Additionally, we use mixed precision training to accelerate the process and reduce memory usage. This technique greatly reduces the training time by taking advantage of the computational power of GPU. However, it will also lead to numerical instability. Gradients might lose precision in 16-bit representation, leading to slower or less accurate convergence. Optimizers like Adam or RMSprop are also highly sensitive to precision issues, which can lead to unstable training or poor performance.

Future work can explore better integrating the CNN with Hebbian layer to reduce the complexity of the current model. By improving the network structure using more lightweight architectures, the numerical instability issues may be alleviated. Also, future studies can pay attention to the system’s robustness to extremely high noise levels, as certain scenarios in the experiments indicated a slight performance drop under intense disturbance.

5. Conclusion

This paper proposes a novel hybrid network model that combins ResNet, UNet and SoftHebbLayer. By synergizing the robust feature extraction capabilities of ResNet with the precise depth reconstruction of the UNet architecture, and leveraging the adaptive capacities of the SoftHebbLayer, the model significantly improves depth estimation performance. Performance evaluations indicate that while our model achieves significant improvements in some metrics such as MSE and RMSE, challenges remain in areas such as absolute relative error. These insights point to the necessity for continued refinement of the model, particularly in enhancing its sensitivity to subtler depth cues and improving its robustness against more complex backgrounds and lighting variations.

In conclusion, the hybrid model marks a significant step forward in the pursuit of more reliable and versatile depth estimation tools. Our work contributes to the broader dialogue on how deep learning architectures can be ingeniously modified and combined, not just for incremental improvements but also for substantial leaps in performance and applicability in real-world applications. The journey to perfect depth estimation continues, and it is hoped that our contributions will serve as a valuable foundation for future innovation.