1. Introduction

Nowadays, with the rapid development of the field of artificial intelligence, the field of artificial intelligence has gradually entered people's vision. A major research goal in the field of Artificial Intelligence (AI) is to achieve fully autonomous agents [1]. The agent can derive optimal behavior based on its environment. Machine learning, as the core technology in the field of artificial intelligence, provides the most basic learning power for the agent. With the unremitting efforts of many scholars, various machine learning algorithms emerge in endlessly. However, since most of the intelligent decision-making algorithms adopt fixed decision-making processes and models, a large amount of computing resources is consumed [2]. Therefore, the exploration of machine learning algorithms is a necessary and important thing.

Reinforcement learning is one of the branches of machine learning. Reinforcement learning endows agents with self-supervised learning ability, enabling them to interact with the environment autonomously and make continuous progress in trial and error [3]. The Markov chain becomes the foundation of the subsequent reinforcement learning algorithm. Markov chain is a random process of transformation from one state to another [4], and the state of the next moment depends only on the current state. In order to interact with the environment in the whole process and win the maximum reward in the environment, a Markov decision process emerged [5]. The action value function defines an expectation that an action taken by a certain state will be rewarded. In order to maximize the rewards for each action, the greedy strategy is adopted during the execution of the action to obtain the optimal action [6]. Watkins et al. proposed the Q learning algorithm by combining the time series segmentation algorithm with other optimization algorithms [7].

Q-Learning algorithm, as a classical reinforcement learning algorithm, is of great significance. Considerable research achievements have been made in topology optimization [8], vehicle networking [9] and information technology [10]. As a model-free prediction algorithm, Q-Learning is mainly used to solve the problems related to Markov decision process. Q-learning algorithm is a relatively intuitive reinforcement Learning algorithm, the key is to construct a rewards table about status-actions, that is, Q table. The table records the rewards brought by each action in each case. In the algorithm, the author will pay attention to the optimal order decision following the Q table [11]. Among all possible actions, the author will select the action with the largest rewards and randomly select the action with a small probability to promote the exploration of the agent.

In this paper, the process restoration and hyperparameter research of Q-Learning algorithm will be carried out, and the "Cliff Walking" problem will be used as a visual effect measurement carrier.

2. Methodology

2.1. Data source and description

Gym is a commonly used Python based reinforcement learning library. This experiment will be based on the example "Cliff Walking" given in gym library to verify the feasibility of the algorithm and debug the algorithm. The "Cliff Walking" environment provides a relatively small number of discrete states and operating Spaces that are easy to learn.

The rule of "Cliff Walking" is that in a 4 × 12 grid, the agent starts at the bottom left corner of the grid and ends at the bottom right corner of the grid, with the goal of moving the agent to the final position (Figure 1).

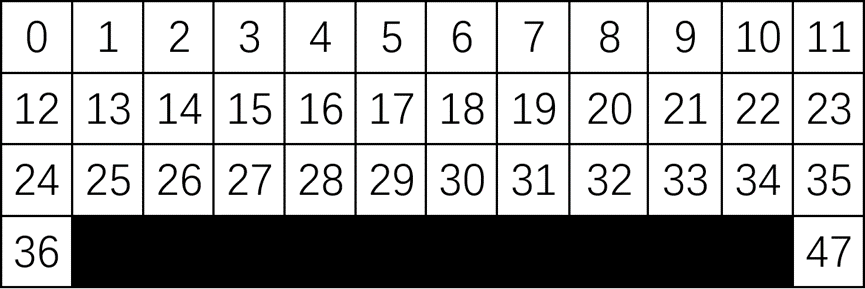
Figure 1. Cliff Walking

This paper limits it to the following:

Restrict 1: The agent is not allowed to move out of the grid, but the action that moves extra toward the network is still recorded as an action and is rewarded with -1 units as if it were a normal action.

Restrict 2: If the agent falls off a cliff, it will return to the starting point and receive a bonus of -100 units.

The goal is to reach the destination in the least number of steps, and it is easy to conclude that optimal solution is reward= -13.

2.2. Indicator selection and description

There are only 4 discrete types of Action Space and 48 discrete types of Observation Space in this experiment.

During the experiment, the following data will be mainly recorded. State is used to record the current state of the environment. Action is used to represent the four discrete motion modes. Reward is used to record the corresponding reward for each state. Epsilon is the probability constant in the greedy strategy. Alpha is the updating amplitude of the data. That is the learning rate. Gamma is the discount factor, used to indicate the degree of discount for future rewards (Table 1).

Table 1. Indicator introduction

2.3. Method introduction

The algorithm chosen in this experiment is Q-Learning algorithm. In essence, Q-Learning algorithm is sequential difference control of different strategies. In the process of learning different strategies, there are two different strategies, goal strategy and behavior strategy. The former is more conservative and similar to the general direction of the whole learning behavior, while the behavior strategy is more radical. This paper chooses the ε-greedy strategy to maintain a certain degree of agent exploration.

In order to implement Q-Learning, this paper needs to create and initialize an action-state table, select and execute an action a, get the current and future rewards, and then update the table through the Bellman equation. Here is the pseudo-code for Q-Learning (Table 2):

Table 2. Q-Learning

3. Results and discussion

3.1. Training results

The algorithm process of Q-Learning was restored through python, and training was carried out. By debugging the program, a usable Q-Learning model is obtained.

In the figure 2, the solid line represents rewards. Since rewards will cause strong shocks due to the uncertainty of the agent's decision, this paper introduces a smoothing reward. The way of Smoothing rewards is to use this \( \ reward(t)\ast0.1\ +reward(T - 1)\ \ast0.9 \) , which will effectively reduce the size of the reward shock. It can be seen from the image that after 250 turns, the reward has been very close to the optimal solution -13, and the subsequent image vibration is due to the fact that this paper sets the minimum coefficient ε of the greed function to 0.01, so it fails to reach the optimal solution of the current situation.

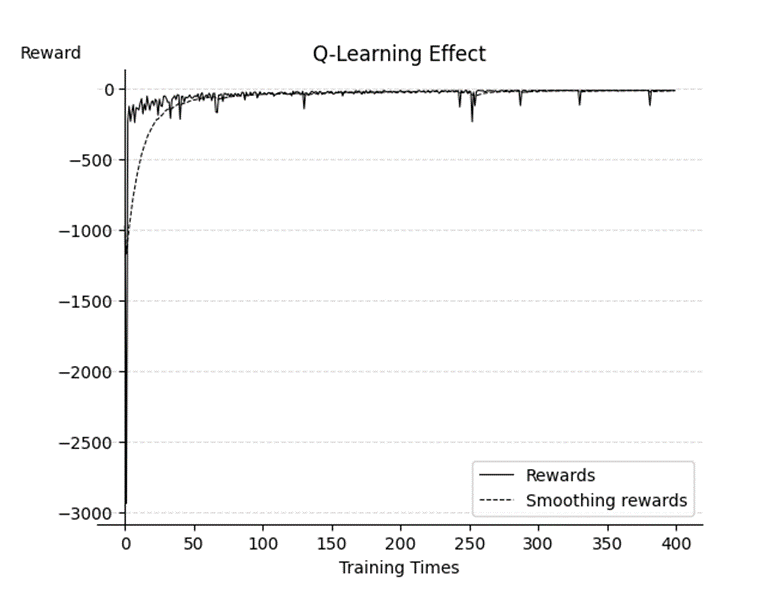
Figure 2. Q-Learning Effect

So, it follows that in the face of such a relatively simple problem, the coefficient ε of the greed function can be as small as possible. The trained model is tested for 30 times, and the test results are as follows (Figure 3).

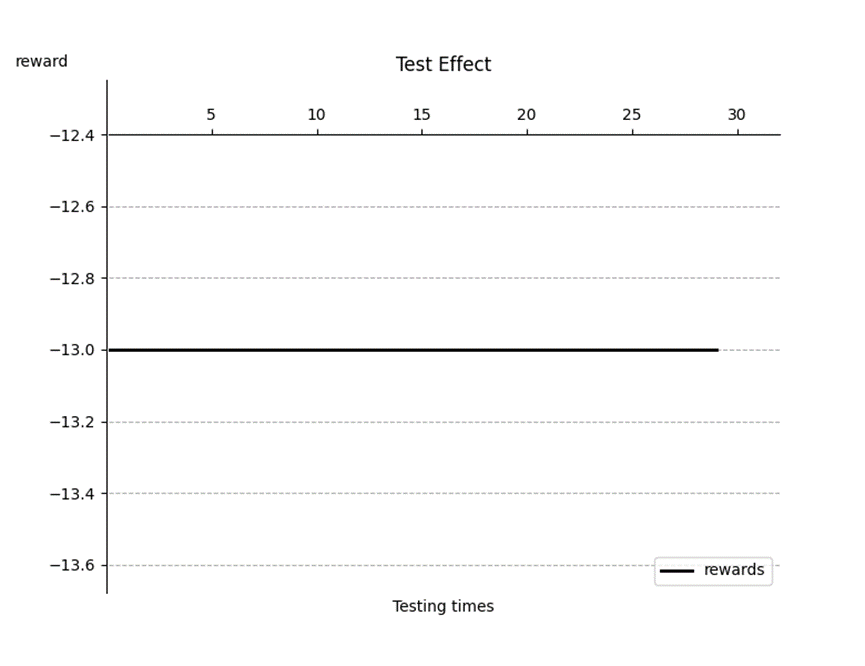
Figure 3. Test Effect

It can be observed that the agent model obtained by Q-Learning is quite good, and the results of 30 tests are all the optimal solution -13.

3.2. Hyperparameter Gamma

Gamma is studied in this experiment. Gamma is the discount factor, indicating how much the agent attaches importance to the future reward, or how much the future reward will affect the current decision. By influencing the decision, the training speed of the model will be affected.

Gamma value from 0.5 to 1.5, step size is 0.01, each gamma value is trained 200 times the full training process. The author believes that training success is defined by the fact that the average value of smoothing rewards for nearly ten consecutive times is greater than -13.1, and the training frequency at this time is recorded. Finally, the average value of 200 complete training times is calculated as the training frequency corresponding to this gamma value. The final training results are as follows (Figure 4):

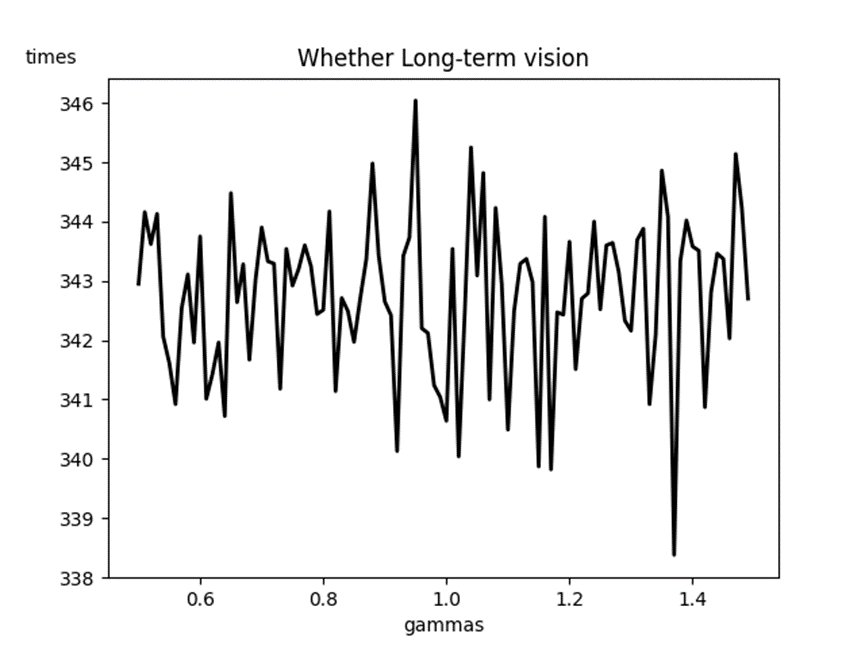
Figure 4. Gamma Effect on the Number of Training Sessions

As can be seen from the figure, the function image vibrates very violently, and the absolute value of the difference between the maximum value and the minimum value is even less than 10 times. It can be seen that in relatively simple experiments like this one, the effect of gamma on the model is much less than that of training times.

3.3. Hyperparameter alpha

Alpha was studied in this experiment. Alpha is the learning rate, which represents the degree of influence of new data on old data in the process of iterating Q-table, and determines whether the model accepts the data aggressively or not.

Gamma is evaluated from 0.1 to 0.5, with a step size of 0.01, and each alpha value goes through the full training process 200 times. The author thinks that training is successful when the average value of smoothing rewards for nearly ten consecutive times is greater than -13.1, record the training times at this time, and finally calculate the average number of 200 complete training times as the corresponding training times of this alpha value. The final training results are as follows (Figure 5):

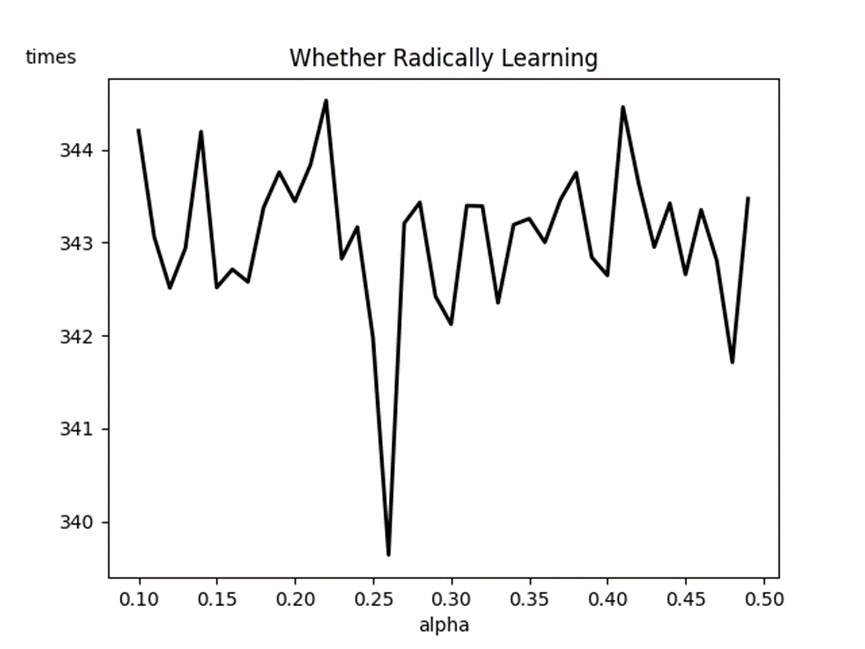
Figure 5. Alpha Effect on the Number of Training Sessions

4. Conclusion

Through the "Cliff Walking" problem, this experiment studies the application of Q-Learning algorithm and the influence of hyperparameter gamma on the entire agent training process, and draws the following conclusions:

The agent model obtained by Q-Learning is quite effective. The results of 30 tests are the optimal solution -13. Before 50 training sessions, the absolute difference between reward and the optimal solution is very large, and then gradually becomes stable, approaching the optimal solution -13 at about 250. In the end, there is a shock phenomenon, which is the random behavior of greedy algorithm that leads it away from the optimal solution.

Gamma-time function image and alpha-time function image oscillate very violently, and the absolute value of the difference between the maximum value and the minimum value is even less than 10 times. It can be seen that in relatively simple discrete model experiments such as this experiment, The effect of gamma and alpha on the model is much less than the effect of training times on the model.