1. Introduction

In the cold and dry winters of northern China, enhancing indoor lighting and heat absorption has become a critical aspect of building energy efficiency. Glass windows, as the primary medium for indoor lighting, significantly impact indoor temperature and lighting conditions due to their transmittance and thermal insulation properties. Sunlight spans a broad spectrum of wavelengths, with the 300-2000 nm range being particularly crucial for indoor heating [1]. Therefore, optimizing the thickness of glass to maximize the transmission of solar energy within this range holds substantial practical value for improving indoor comfort and reducing heating demands in cold climates.

Recent advancements in the study of light transmission and thermal insulation properties of multilayer windows have highlighted the significant influence of glass thickness and layering on the optical properties of windows. Research by Garlisi et al. demonstrated that solar radiation is affected by the optical characteristics of glass, including transmittance, absorbance, and reflectance, which can be further modified by coatings [2]. Additionally, employing multilayer glass structures has been shown to enhance the control of solar radiation effectively. Sun et al. reported that double glazing could reduce heating energy consumption in buildings, contributing positively to energy conservation and heat retention during winter in cold regions [3].

Intelligent optimization algorithms have gained significant attention in the design of building materials and structures, particularly for their capability to address complex optimization challenges. The Artificial Fish Swarm Algorithm (AFSA) has emerged as a powerful tool in material science and engineering, owing to its robust performance in optimizing intricate design problems [4]. For instance, Huang et al. utilized a modified AFSA to optimize the layout of fiber Bragg grating sensor networks, achieving improvements in convergence accuracy, speed, and network coverage, thus demonstrating the algorithm's potential for optimizing complex structural designs [5]. Building on this context, the current study establishes a transmittance model for solar energy passing through glass within the 300-2000 nm range using theoretical analysis and experimental data. The research employs AFSA to optimize the thicknesses of triple glazing (L1, L2, and L3) by iteratively updating the combination of thicknesses to maximize incident solar energy. This study aims to provide both theoretical insights and practical guidance for the energy-efficient design of building heating systems in cold regions [6].

2. Models and methods

2.1. Glass transmittance model

The optimization objective of this study is to maximize the amount of solar energy entering the room through the glass by adjusting the thickness of the triple glazing (L1, L2, L3). The process of incident light entering the room through the triple glazing can be viewed as the model shown in Figure 1:

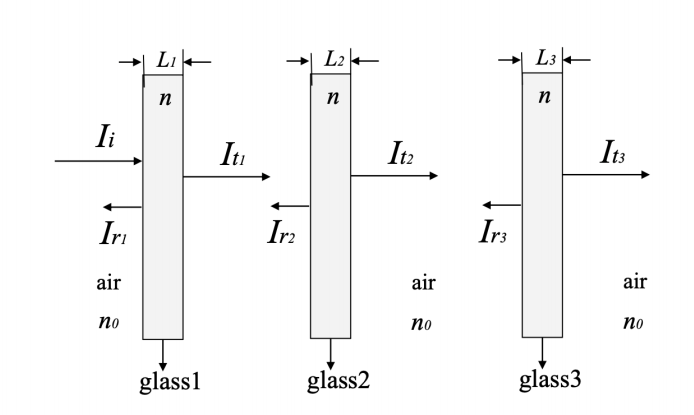
Figure 1. Transmission and reflection of sunlight on triple glazed surfaces (Photo credit: Original).

Let the refractive index of the glass material be n and the refractive index of air be n0. The reflectance R can be calculated by the following formula:

\( R={(\frac{n-{n_{0}}}{n+{n_{0}}})^{2}} \) (1)

For each wavelength λ of the incident light, the transmission energy can be calculated from the transmittance T of the glass:

\( T=\frac{{I_{t}}}{{I_{i}}}=\frac{{(1-R)^{2}}}{{(1-R)^{2}}+4R{sin^{2}}(kL)} \) (2)

Where k is the wave number and L is the thickness of the glass. The variation of transmission coefficient with wavelength for single-layer glass is shown in Figure 2:

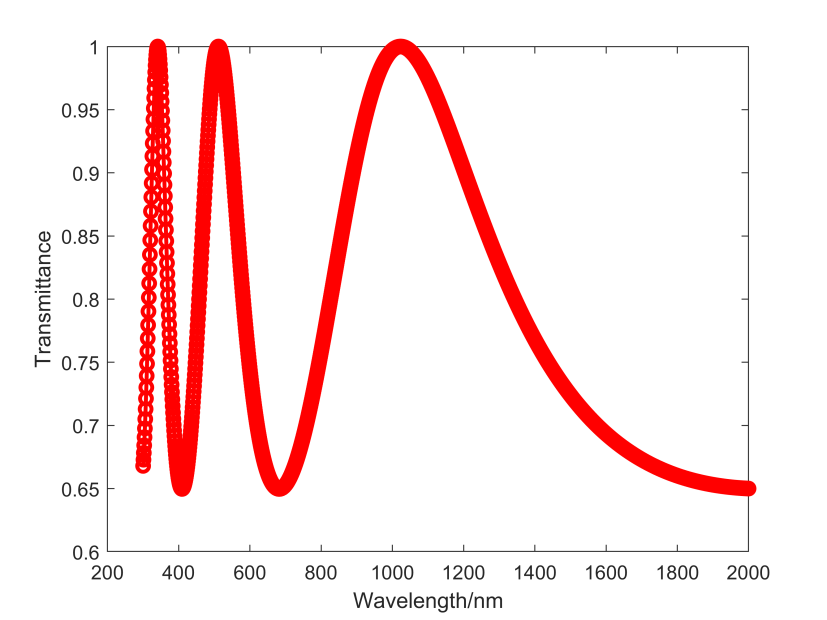
Figure 2. Variation of transmission coefficient of single-pane glass (Photo credit: Original).

Assume that the incident spectral intensity of sunlight \( {I_{i}} \) follows a Gaussian distribution, the center wavelength of the incident spectrum is \( {λ_{0}} \) (580 nm), the maximum incident intensity is 1000, and the standard deviation is σ [7]. The incident intensity model is formed as shown in Figure 3. \( { I_{i}} \) of the incident light intensity model is shown in Figure 3:

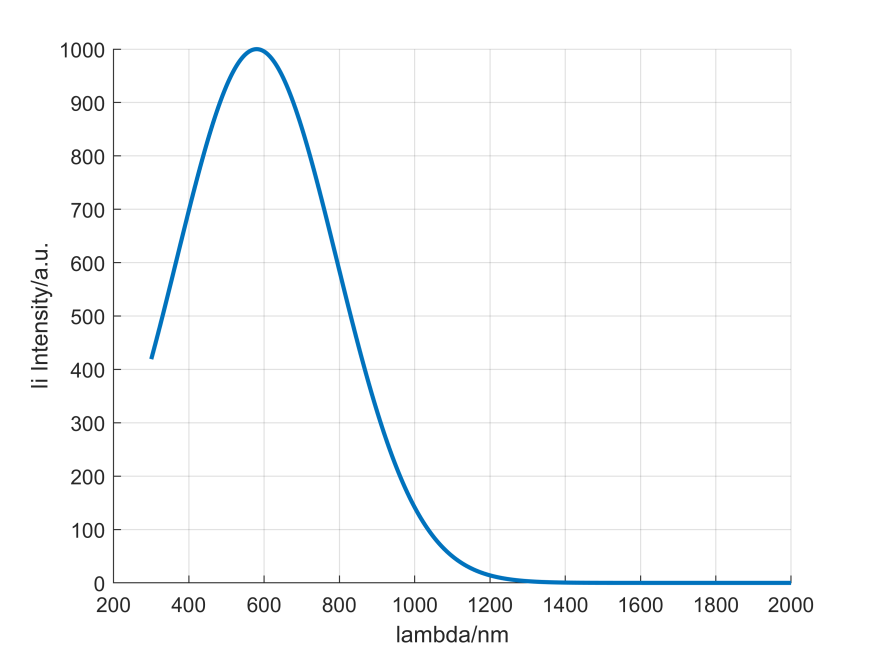
Figure 3. Gaussian distribution of incident light intensity (Photo credit: Original).

The expression for the incident spectral intensity is:

\( {I_{i}}=1000exp{(-\frac{(λ-{λ_{0}}{)^{2}}}{2{σ^{2}}})} \) (3)

The standard deviation σ is calculated as:

\( FWHM=2\sqrt[]{2ln2}∙σ \) (4)

FWHM is Full Width at Half Maximum, which is set to 500 nm [8].

For each layer of glass, the transmitted light intensity can be obtained by integrating a Gaussian distribution. Total incident energy \( {E_{total}} \) is the sum of all transmitted light intensities in the wavelength range of 300-2000 nm:

\( {E_{total}}=\sum _{300nm}^{2000nm}I(λ){T_{1}}(λ){T_{2}}(λ){T_{3}}(λ) \) (5)

The objective is to optimize the combination of thicknesses of L1, L2, and L3 by making the \( {E_{total}} \) reach the maximum.

2.2. Introduction to AFSA

Artificial Fish Swarm Algorithm (AFSA) is a bionic swarm intelligence optimization algorithm that simulates the collaboration and competition of a school of fish in behaviors such as prey, following, and swarming. The algorithm ultimately converges to the global optimal solution through the movement and position updates of each artificial fish within the search space. Figure 4 shows the flowchart of the algorithm:

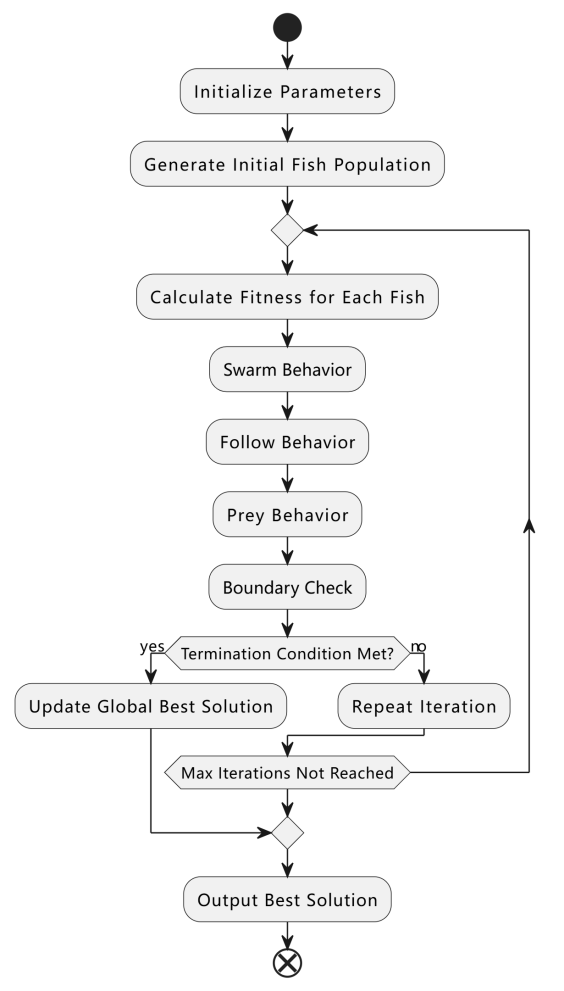
Figure 4. Flowchart of artificial fish swarming algorithm (Photo credit: Original).

The main behaviors of AFSA include:

Swarming behavior: fish decide whether to move together or not based on the location and fitness values of neighboring fish.

Following behavior: fish decide whether to follow the movement based on the position of the most adapted fish in their sensory range.

Prey behavior: fish explore the search space randomly to find more optimal food locations.

These behaviors ensure that the algorithm strikes a balance between global and local search by dynamically adjusting parameters such as step length, visual range, and crowding factor.

2.3. Algorithm implementation

In this study, the detailed implementation steps of the AFSA are as follows:

Initializing the fish swarm: Generate a certain number of artificial fish that are randomly distributed in a search space of three glass thicknesses. The position of each fish represents a set of glass thickness combinations.

See the `AF_ init` function for code implementation.

Calculation of the fitness function: the fitness value, i.e., the total energy incident into the room at the current thickness combination, is calculated for each fish based on the previous transmittance model.

See the `AF_ foodconsistence` function for code implementation.

Behavioral update: Each fish dynamically adjusts its position according to swarming, following and prey behaviors, gradually converging to the global optimal solution.

See `AF_ swarm`, `AF_ follow`, `AF_ prey` functions for code implementation.

Boundary check: Ensure that the position of each fish is within reasonable physical limits, i.e. that the thickness of each pane of glass does not exceed the upper and lower limits specified in the design (between 1 mm and 10 mm).

The code implementation is shown in the boundary checking logic in each function.

3. Results and discussion

3.1. Parameter setting

In the optimization algorithm, the number of fish population is set to 50 and the maximum number of iterations is 50. To improve the algorithm convergence, the perceived range(visual), the step size (step) and the crowding factor (delta) are set to 0.01, 0.001 and 0.00518 respectively. The thickness of the glass is set within the range of 1 mm to 10 mm, and the validity of the combinations of these parameters is tested through several runs.

3.2. Optimization results

The algorithm finally converges to a set of glass thickness combinations, L1, L2, and L3 of 0.0058 m, 0.0060 m, and 0.0058 m. With this set of thickness combinations, the solar energy incident to the room is maximized. At this time the energy intensity of incident sunlight penetrating the three layers of glass into is shown in Figure 5:

Figure 5. Optimized energy incidence intensity of triple glazing (Photo credit: Original).

The maximum value obtained is 387495.22. The optimization process of the algorithm is shown in Figure 6: This result demonstrates the strong capability of AFSA in such multi-peak optimization problems. In addition, by comparing the optimization results under different parameter configurations, it can be observed that:

The setting of the step size has a significant impact on the convergence speed and final result of the algorithm [9]. While a larger step size speeds up convergence and avoids falling into a local optimum, it also increases the risk of missing the global optimal solution, as the algorithm may not be able to perform sufficiently fine searches close to the optimal solution.

The perception distance affects the global search ability of the fish population. A larger perception distance enhances the global search capability of the algorithm, but may also lead to a search space that is too large to converge.

The crowding factor plays a key role in controlling the degree of fish aggregation. A smaller crowding factor encourages fish to disperse and thus explore the entire search space more fully. As shown in Figure 6.

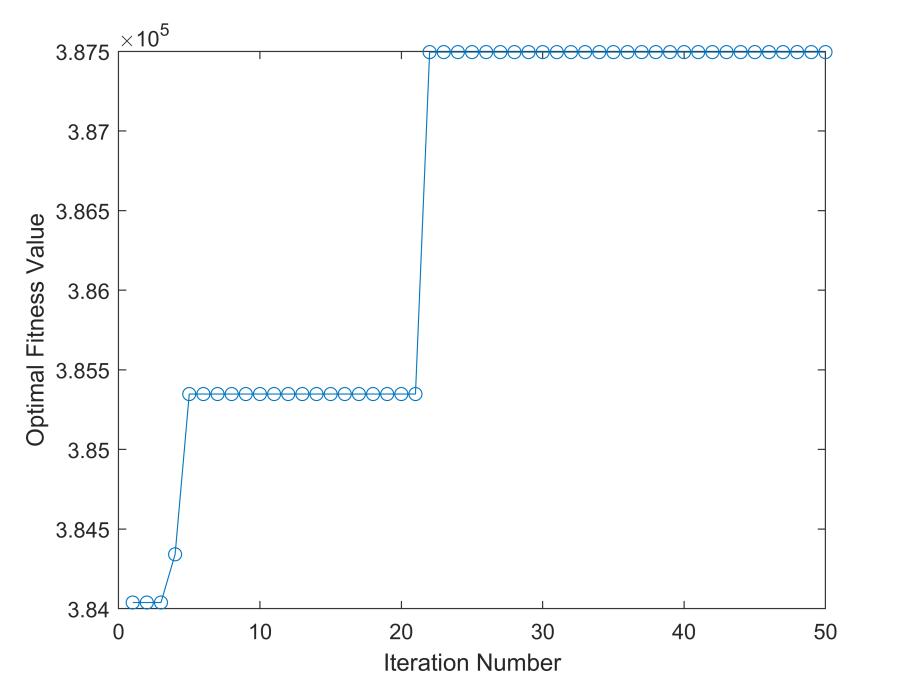
Figure 6. Iterative process of artificial fish swarm algorithm (Photo credit: Original).

3.3. Discussion

Although the optimization results show that the AFSA performs well in the triple glazing thickness optimization problem, there are still some issues that need to be further explored:

Initial fish distribution: in the multidimensional search space, the initial distribution of fish has a large impact on the final convergence result. How to effectively generate diverse initial solutions is an important direction for subsequent research.

Improvement of the fitness function: the current fitness function only considers the transmitted light intensity, and in future study, factors such as heat transfer and manufacturing costs can be considered to formulate a multi-objective optimization problem [10].

Comparison of multiple algorithms: artificial fish swarm algorithm can be compared with other intelligent optimization algorithms such as genetic algorithm and particle swarm optimization to explore the strengths and weaknesses of different algorithms in solving such problems.

4. Conclusion

This study successfully applied the Artificial Fish Swarm Algorithm (AFSA) to optimize the thickness of triple glazing, maximizing solar energy transmission within the critical wavelength range of 300-2000 nm. By developing a detailed transmittance model and iteratively adjusting the glass thicknesses, the research demonstrated the significant impact of optimal glazing configurations on enhancing indoor heating efficiency in cold northern climates. The results confirm the efficacy of AFSA in addressing complex optimization challenges in building material design, providing valuable theoretical support and practical guidance for energy-efficient architectural solutions.

Future research could focus on expanding this study in several directions. Multi-objective optimization should be explored to incorporate additional factors such as thermal insulation properties, manufacturing costs, and environmental impacts, creating a more comprehensive design approach. Enhancing the AFSA with adaptive techniques, such as dynamic step sizes and variable sensing ranges, could further improve its global search capabilities and accuracy in complex optimization tasks. Practical application verification, including laboratory testing and real-world building trials, is also crucial to validate the optimization results and ensure the proposed designs perform effectively under actual conditions. These future directions will deepen the understanding of advanced optimization algorithms in sustainable building design, contributing to the development of more energy-efficient and environmentally friendly construction technologies.