1. Background

In modern control theory, PID (Proportional-Integral-Differential) control, as a classical control strategy, is widely used in industrial control systems because of its simple structure, easy to understand and implement. PID controllers control the error of the system through the interactions of the proportional, integral and differential links to achieve precise control of the system output. However, when applied to systems with time-varying and nonlinear characteristics such as intelligent trajectory trolleys, traditional PID controllers face some limitations. During the operation of an intelligent trajectory trolley, the control of its speed and direction is affected by a variety of factors, such as road conditions, vehicle dynamics, and external disturbances[1]. These factors make the dynamic behaviour of the trolley complex and it is difficult to achieve accurate control with traditional PID control algorithms[2].

Yajiang Du et al [3] combine the multi-valued logic control of Pan-Boolean algebra with PID algorithm to construct a multi-valued logic controller based on Pan-Boolean algebra, and the experimental results show that compared with the traditional PID control, the Pan-Boolean PID control has a better stability, faster response and smaller overshooting, but the parameter adjustment is more complicated. Changjian Zhang et al [4] proposed a composite control method combining fuzzy control and PID algorithm applied to quadrotor UAV dynamics model, simulink simulation results show that compared with traditional PID control, the system under fuzzy PID control has faster response speed and higher control accuracy and sensitivity, but the dependence on the expert is stronger and there is a certain degree of blindness. Xiaogan Zheng et al [5] proposed a fuzzy fractional-order PID control algorithm based on improved particle swarm algorithm to optimise the robot motion controller, and the comparative analysis results show that the particle swarm optimised fuzzy PID control has a faster control response and better stability compared to the ordinary PID and the general fuzzy PID, but the pre-testing time is a little longer. Observing the previous research, it is not difficult to find that the existing methods have a greater dependence on the PID adjustment parameters, and this process requires the accumulation of rich experience, which makes it difficult for beginners to get started.

With the rise of artificial intelligence technology, especially the deep learning technology that has emerged in recent years, it also provides a new optimisation pathway for PID control. Neural networks are able to discover the intrinsic laws and nonlinear relationships of the system by learning a large amount of data, so as to adjust and optimise the parameters of the PID controller online and improve the control performance. Ziyu Guo et al [6] proposed a PID control strategy based on fuzzy radial basis function (RBF) neural network, compared with the simulation results of other controllers to obtain, the fuzzy RBF neural network controller that effectively combines the fuzzy PID and the RBF neural network, to achieve the output of real-time calibration of the PID parameters, and the speed control of stepping motors is more rapid and accurate, but there is also a large dependence on the parameter settings and population size, requiring professional personnel to control the stepping motor. However, it also has the problem of large dependence on parameter setting and population size, which requires professional personnel to continuously adjust and optimise.

Therefore, if PID control can be combined with fuzzy control, neural network and other intelligent optimisation algorithms, it has become a research hotspot in the field of closed-loop control of intelligent trajectory trolley[7]. This method of integrating multiple control strategies can not only improve the control accuracy of the running speed and direction of the trolley, but also enhance the robustness and adaptability of the system, which is of great significance for promoting the development of intelligent trajectory trolley and even the whole intelligent control system[8-9].

In this paper, the Bayesian optimisation algorithm is combined with PID control to present a study on the application of Bayesian optimisation and PID control in intelligent trailing vehicle. The Bayesian optimisation algorithm pre-searches the three parameters of PID within the specified range to obtain the initial Kp, Ki, Kd, and further updates the parameter increments of PID online using the objective function to output the optimal PID parameter values, and builds a closed-loop control simulation model of intelligent tracing vehicle using Python to simulate and verify the Bayesian optimisation improved traditional PID algorithm, and finally builds a Finally, the closed-loop control experimental platform of intelligent trajectory trolley is built for further experimental verification, which proves that the algorithm has good dynamic performance.

2. Fundamentals

2.1. PID Control Algorithms

PID control consists of three parts, namely, proportional part, integral part and differential part. Proportional part (P) is based on the set value and the actual value of the difference (i.e., the size of the deviation) to a certain proportion of the control volume, its role is to adjust the control volume according to the size of this deviation initially, so that the system can more quickly reach the set value. The integral part (I) is the accumulation of the deviation and adjusts the control quantity according to this accumulation, and its function is to eliminate the steady state error of the system and ensure that the system is stable near the set value for a long time. The differential part (D) is the rate of change of the deviation to adjust the control quantity, and its role is to predict the future deviation changes, and reduce the overshooting and oscillation of the system.The PID controller obtains the final control quantity by adding up the outputs of the three parts, whose mathematical formula is[10]:

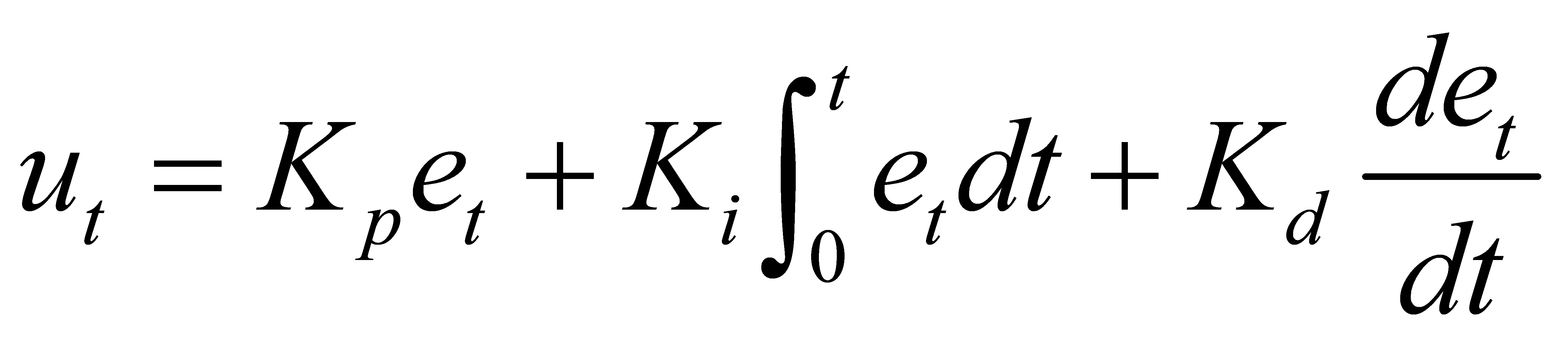
(1)

where ut is the control quantity, et is the deviation, Kp is the proportionality coefficient, Ki is the integration coefficient, and Kd is the differentiation coefficient.

The block diagram of the PID control system is shown below:

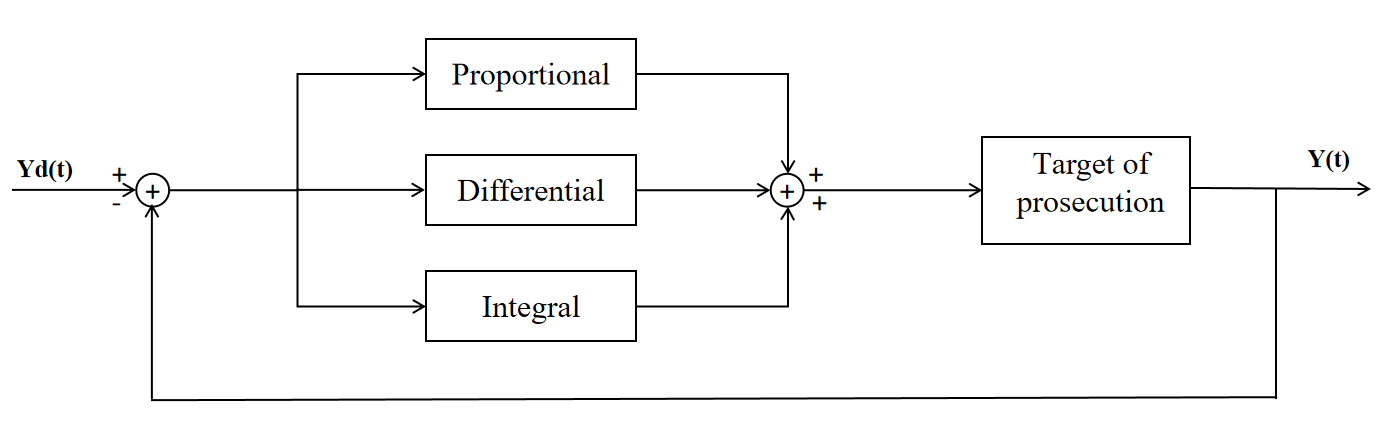
Figure 1. Block diagram of PID control system

2.2. Bayesian Optimization

Bayesian Optimization is a method of searching for global extremes of an objective function based on the guidance of Bayes' theorem, in which an iteration is carried out by observing the results of the historical iterations and searching for the optimal solution on the basis of merit. Bayesian optimisation is implemented in the form of surrogate optimisation, where both the objective function f(x) and its derivatives are unknown, and a function that approximates the original objective function is fitted by constructing a surrogate function, capturing multiple points near the extremes, and continuously updating the surrogate function[11]. Bayesian optimisation achieves finding a better solution in a finite amount of time, which is an obvious advantage over relatively inefficient and time-consuming methods such as Ant Colony Algorithm and Genetic Algorithm.The process of Bayesian optimisation is[12]:

(1) Initialise a prior distribution for the agent function;

(2) Select appropriate data points x such that the acquisition function a(x) achieves the maximum value;

(3) Substitute the objective function c(x) to evaluate the data point x and obtain its result y;

(4) Update the proxy function using this new data (x,y) to obtain a posterior distribution that serves as the prior distribution for the next step;

(5) Repeat the above steps until the maximum number of iterations is reached.

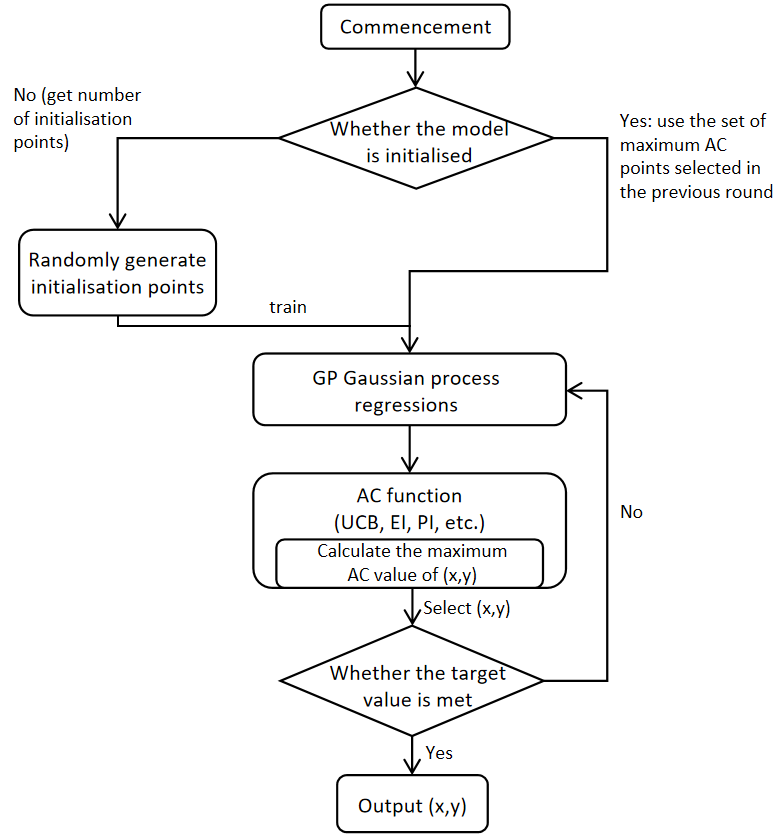
Figure 2. Bayesian optimisation flowchart

Among them, the Prior Function mainly adopts Gaussian process regression, while the Acquisition Function needs to continue searching near the current minimum, making it possible to reasonably utilise the current developed region (Exploitation), and also needs to search in the unsearched region, i.e., exploring the undeveloped Exploration), so as to improve the probability of obtaining the global optimal solution, which mainly includes UCB (Upper confidence bound), PI (probability of improvement) and EI (Expected improvement)[13].

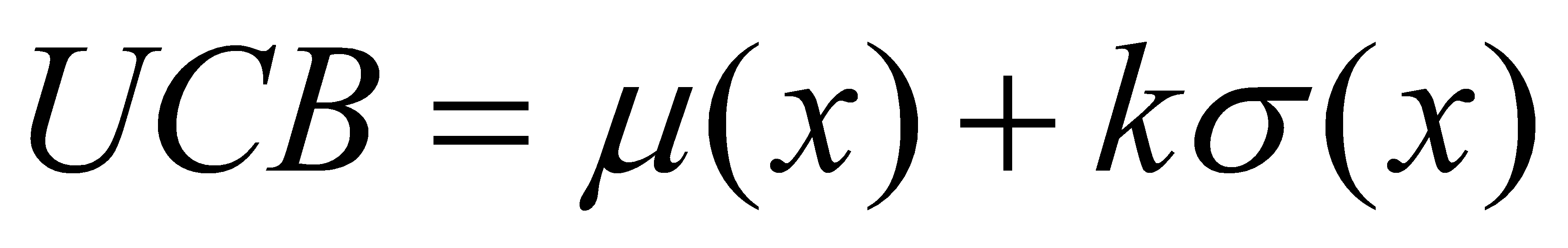
(2)

where k is the conditioning parameter, i.e., the upper confidence bound, μ(x) is the mean of all observations, and σ(x) is the standard deviation of all observations.

(3)

where the hyperparameter υ is used to regulate Exploitation and Exploration, υ = 0 tends to converge around f(x+), Φ denotes the normal cumulative distribution function, and f(x+) denotes the maximum value available.

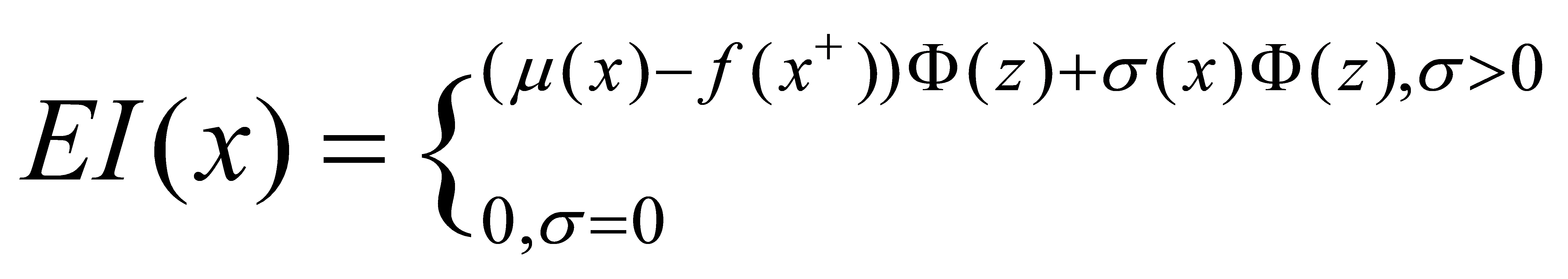
(4)

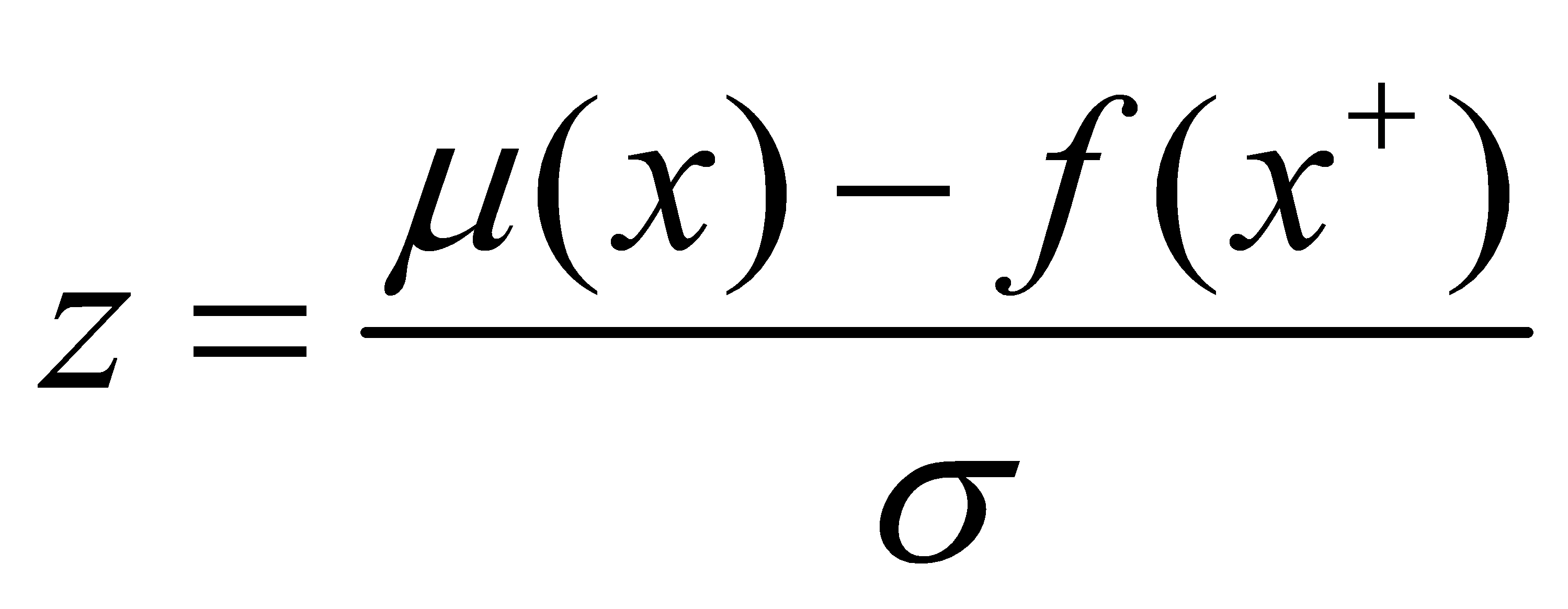
(5)

The EI function solves for the expectation that the value of the function at the unknown point is larger than f(x+), taking into account the question of how much larger the unknown point is than the largest known point[14].

It can be seen that the core of Bayesian optimisation lies in the construction of the prior and acquisition functions.

3. Modelling

The conventional control differential equation for PID (Proportional-Integral-Differential) control is as follows:

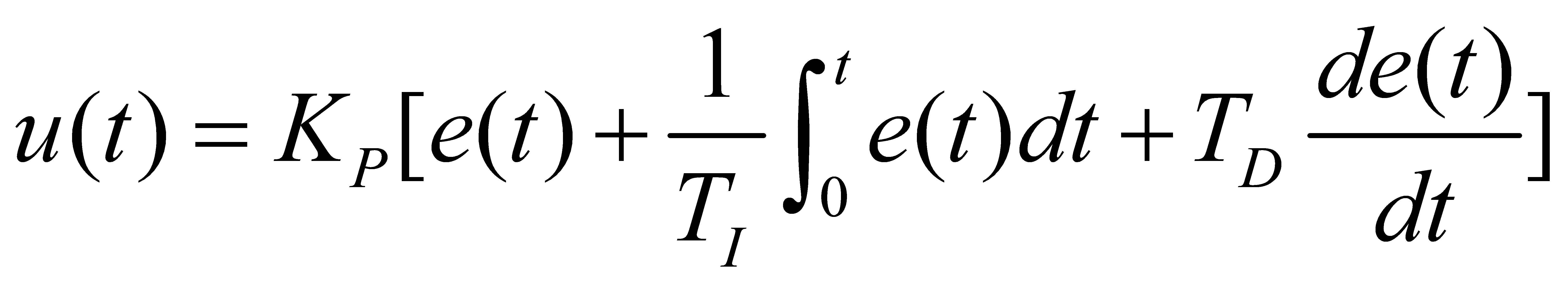
(6)

Where t is the time interval required from the start of regulation to the output of the current control quantity, e(t) denotes the amount of deviation between the given value and the controlled variable, KP is the proportional gain, TI is the integration time and TD is the differential time[15].

In control system design, the parameter settings of PID controllers have a crucial impact on system performance. Traditional PID parameter tuning usually relies on empirical or trial-and-error methods, which are not only time-consuming and labour-intensive, but also often do not guarantee to find the optimal parameter combinations. Bayesian optimisation provides a more efficient method of parameter tuning, which is able to find a near-optimal solution through a smaller number of trials.

With the help of Simulink, PID control can be realised, where control signals are calculated in accordance with the set P, I and D parameters and applied to the control system. Bayesian optimisation is performed by constructing the posterior distribution of the objective function in the parameter space. It starts by building a Gaussian process model based on some initial evaluation points and then selects the next most promising point for evaluation based on the predictions of this model. This process is carried out iteratively, gradually reducing the search space until an optimal solution is found[16].

A set of values of P, I, and D is set randomly, the PID control system is run, and each sample point is selected to record the corresponding performance index under the determined value interval. Based on the data of the sample points, a Bayesian probabilistic agent model is established and an evaluation function is defined to quantify the performance of the PID control system. The difference between the corresponding sample point indicator Pi(i=1,2,3,……,n) and the expected final value P0, Hi(t), can be calculated from the following equation, respectively:

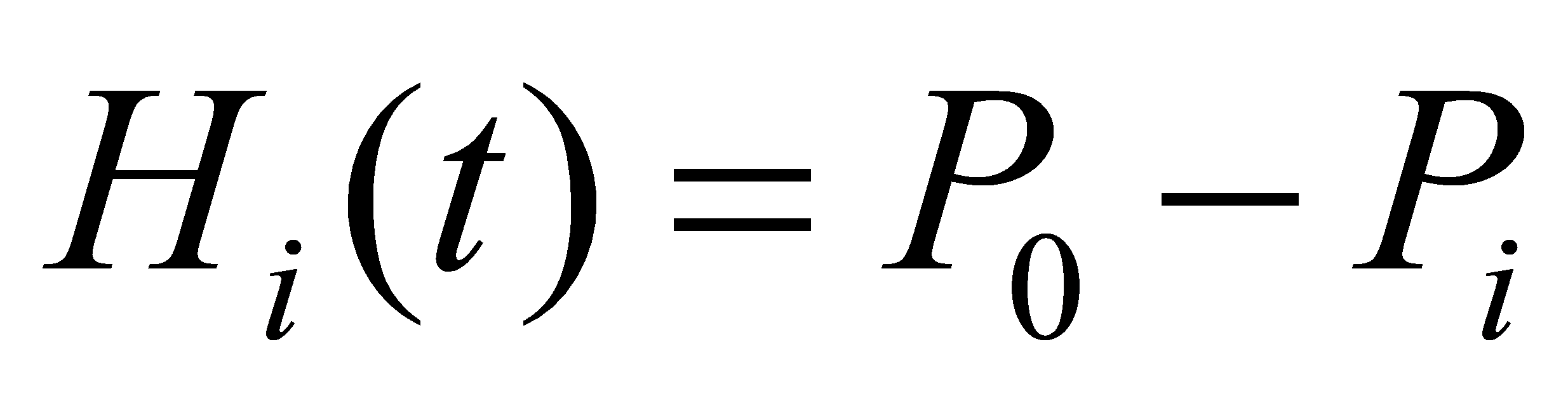
(7)

The individual differences obtained are averaged to obtain the loss function output value H(t) corresponding to the set of P, I and D parameters[17]:

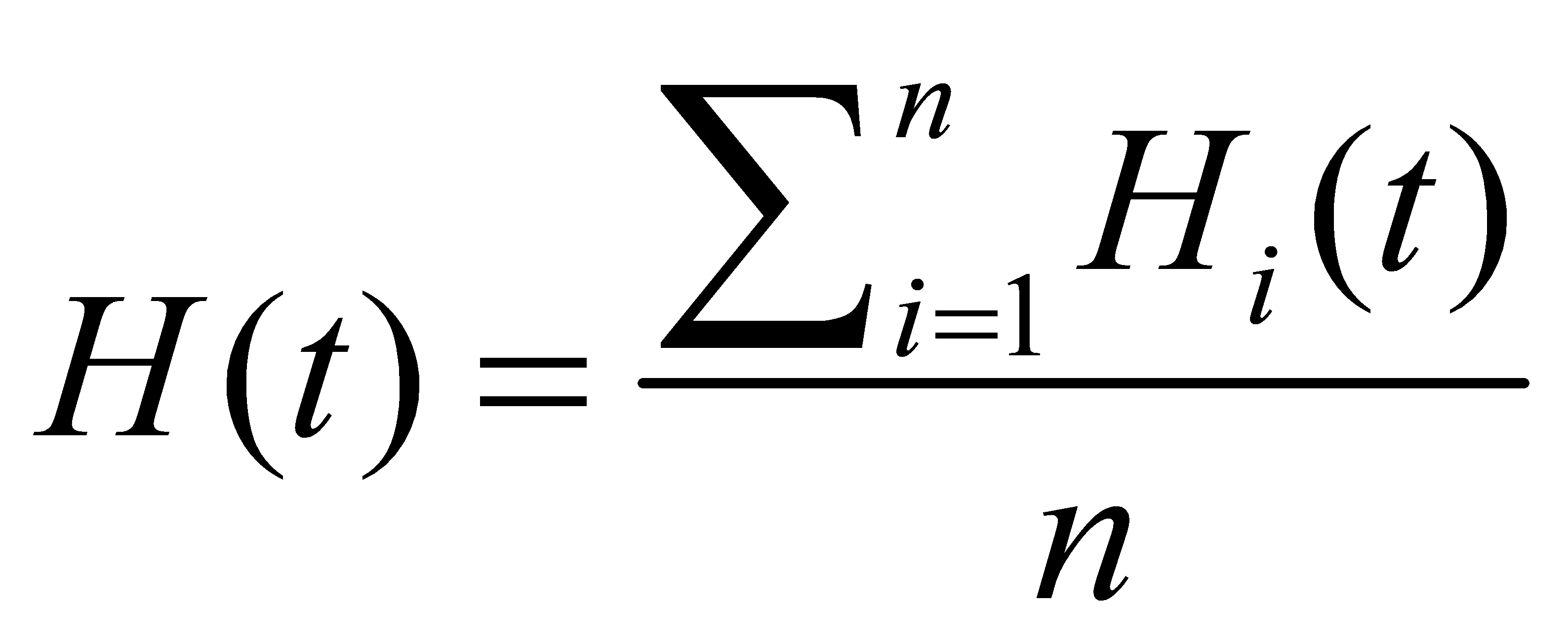
(8)

where n is the number of sample points.

Repeat the above steps to select a new combination of P, I, and D parameters, and after re-running the PID control system, record the new performance metrics and calculate the corresponding new loss function output values until the preset number of iterations is reached or the system satisfies the convergence conditions. The Bayesian optimisation process is analysed to find the minimum objective loss function value MIN[H(t)], thus determining the optimal P, I, D parameter combination[18].

The optimised P, I and D parameters are validated using test data sets to ensure that the control performance is maintained at a better level under different operating conditions. The finally obtained optimised parameters can be implemented into the actual control system to enhance the overall performance and reliability of the system.

Therefore, Bayesian optimisation provides an efficient and automated solution for parameter tuning of PID controllers in hyperparameter tuning of PID control. Through the iterative modelling and optimisation process, the optimal PID parameter combinations can be gradually approximated, thus significantly improving the system performance.

4. Data analysis

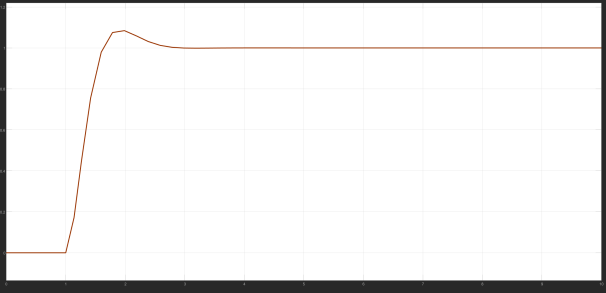
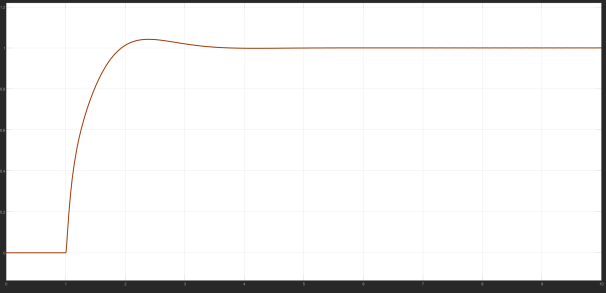
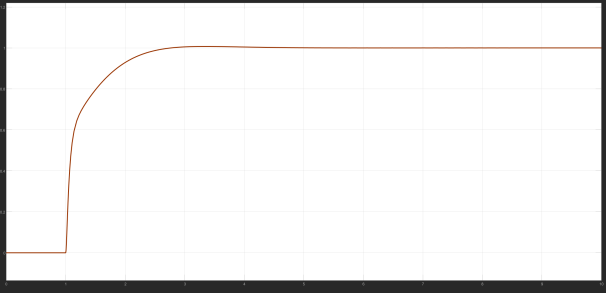
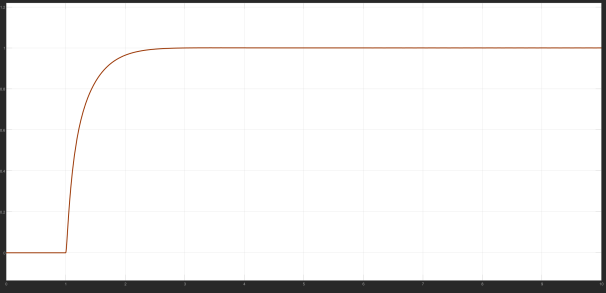
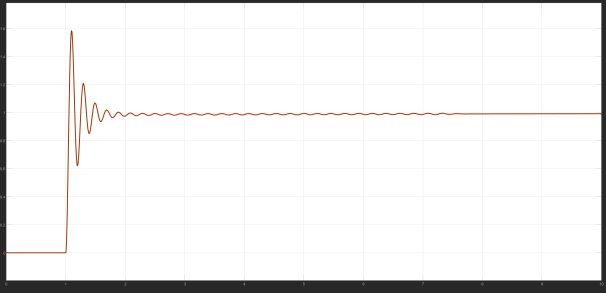
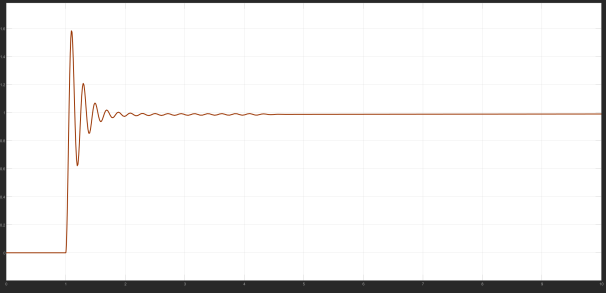
For the stepper motor speed problem, brought into the model, the Bayesian process will be based on different control results, different PID control parameter adjustment, the different iteration number of control results for the output, the final output control image is as follows:

Number of Iterations=10	Number of Iterations=15
Number of Iterations=30	Number of Iterations=35
Number of Iterations=100	Number of Iterations=120

According to the graph, it can be found that the operating curve of the motor is constantly stabilising, and its parameters are constantly being adjusted, and the optimal control parameters are finally obtained as P = 1025, I = 42 and D = 0, when the stability of the control is best.

At the same time, in order to prove the stability of the model, the number of iterations and the image of the loss function are analysed, and it is found that in the case of a shorter number of iterations, a better control effect can be obtained, so it is considered that the model has a better stability.

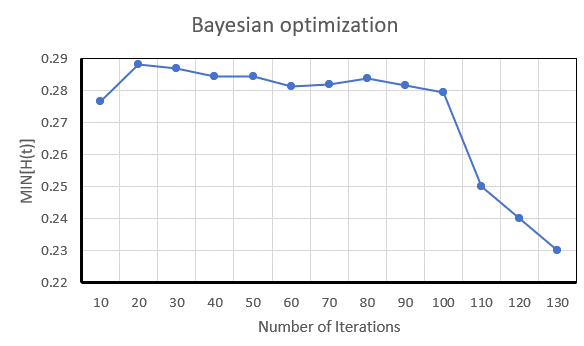
Figure 3. Loss function for Bayesian optimisation

In order to prove the stability of Bayesian optimisation, the use of traditional random forest algorithms for the comparison of experimental conclusions, the use of the same data for the iteration, found that although the random forest can also be output in a relatively short period of time the optimal solution, but the control effect is not stable, in the actual control process there is no way to achieve stable control, for the operation of the motor will cause damage, so that this paper is considered to be better control of the model has a better control of the robustness[19].

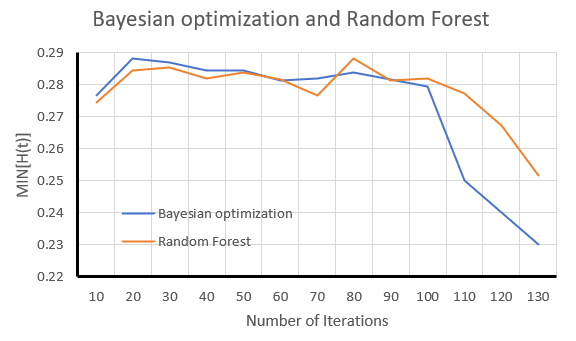
Figure 4. Bayesian optimisation versus random forests

As a result, Bayesian optimisation is able to continuously learn and correct the prior distribution by constructing a probabilistic model of the parameter space, thus gradually approaching the real optimal parameter region. This data-driven optimisation approach can significantly improve the adjustment accuracy of PID parameters and achieve better control results. This method has significant advantages over traditional PID control methods. In traditional PID control methods, parameter adjustment often requires a large number of experimental iterations, and each adjustment needs to be verified in actual operation, which is a time-consuming and costly process. In contrast, Bayesian optimisation, guided by a probabilistic model, can effectively reduce unnecessary sampling and quickly locate the potentially optimal region. This means that in a shorter period of time, Bayesian optimisation is able to find more appropriate parameter configurations, greatly speeding up the design and debugging process of PID controllers.

5. Conclusions

In the realm of intelligent trajectory trolleys, optimizing dynamic operations is vital for performance enhancement. Traditional PID control methods face significant limitations in adapting to the dynamic characteristics of complex systems. To address this, this paper introduces a novel approach utilizing Bayesian optimization to construct a hyperparametric optimization model for predicting optimal PID controller parameters.

Given the variable operating environments of intelligent trajectory trolleys, conventional PID control struggles to adjust parameters in real-time, impacting performance and efficiency. The proposed Bayesian optimization framework effectively navigates high-dimensional search spaces, continuously updating the understanding of unknown functions based on prior knowledge and observations. This iterative process allows for efficient identification of optimal hyperparameters.

A comprehensive comparison with advanced optimization algorithms, including fuzzy control and neural networks, demonstrates the superior prediction accuracy and reduced computational time of the Bayesian hyperparametric optimization method[20]. This highlights its significant contributions to enhancing PID controller performance in intelligent trajectory trolleys.

However, the research acknowledges limitations related to the dataset's size and diversity. Future work should aim to incorporate broader data sources and larger datasets to further validate and enhance the applicability of Bayesian hyperparametric optimization methods in this field[21].