1. Introduction

As the realm of quantum computing advances rapidly, its profound capabilities pose unprecedented challenges to current cryptographic systems which rely predominantly on classical algorithms. Quantum algorithms, particularly Shor's and Grover's, have demonstrated potential to drastically speed up the decryption processes, rendering the conventional cryptosystems vulnerable to attacks. The growing concern hinges on the fact that quantum computers could soon feasibly break the encryption that safeguards everything from government secrets to personal data. The urgency to adapt and enhance cryptographic resilience is thus pivotal to securing digital communications in the quantum era.

Current research has pivoted towards developing Post-Quantum Cryptography (PQC) to counteract the looming quantum threats. The National Institute of Standards and Technology (NIST) has been at the forefront, spearheading efforts to standardize PQC solutions that promise robust security against quantum decryption tactics. Despite significant progress, the transition from traditional to post-quantum cryptography involves complex challenges ranging from technical implementation to organizational adoption. These include ensuring the new cryptographic standards are compatible with existing systems and understanding the resource implications of adopting such standards.

This paper delves into the practicalities and implications of migrating to PQC, anchored by a thorough analysis of the quantum computing principles that threaten modern encryption methods. [1] We outline NIST's timeline for PQC standardization and discuss the technical and strategic considerations for adopting these standards. [2] Moreover, we explore the specific vulnerabilities of both symmetric and asymmetric cryptography in the quantum context, providing a detailed assessment of how quantum algorithms could potentially exploit these systems. [3] Finally, the paper proposes a framework for beginning the migration to PQC, emphasizing the need for proactive organizational strategies to manage the transition effectively, thus ensuring continued data security against future quantum capabilities.

2. Cryptography overview

In the electronic key system, cryptography is used to maintain the security of digital environments. It guarantees the security in three ways: 1) Confidentially. It ensures that no third party can comprehend the message being transmitted. 2) Integrity. It guarantees no third party can alter the message without triggering detection. 3) Authenticity. It prevents third party from imitating the communicating parties.

2.1. Symmetric key cryptography

Bob receives the ciphertext and decrypts it using the same key with the decryption algorithm:\( m=D\left(k,\ m\right) \). The name ‘symmetric-key' stems from the identity of the key in Alice's and Bob's hands. Symmetric-key algorithms implement fastest among all the algorithms in software and hardware and is typically useful when processing large data set [1]. In order to make sure Alice and Bob securely share the key\( k \), there should be a channel for this transition to guarantee the confidentially of the key. This leads to the usage of public keys. As show in the table 1.

Table 1. Notations for symbols mentioned in the digital signature algorithm.

2.2. Asymmetric key cryptography

Each party holds a private key, known only to them, and a public key, which is available to others. If Alice wants to transmit message to Bob, she first acquires the public key generated by Bob and encrypts the message. Bob receives it and decrypts it with the private key to recover the message. It means that everyone can message to Bob with the public key, but no third party can read the content of the message. This guarantees the authenticity of the transmission. RSA is a commonly used algorithm in asymmetric key cryptography and its process is illustrated in the following content.

Firstly, the party generates the keys. Two random large distinct primes,\( p \)and\( q \)are selected. The numbers should be large but have similar bit size to increase the security level. Then compute\( n=p\ \times\ q \)and\( \emptyset\left(n\right)=\left(n - 1\right)\times(q - 1) \).\( \emptyset\left(n\right) \)represents a number smaller to\( n \)and is co-prime with\( n \). The following step requires selecting the public key\( e \), which is an integer satisfying\( 1\text{<}e\text{<}\ \)\( \emptyset\left(n\right) \)and\( \gcd{\left(e,\ \emptyset\left(n\right)\right)}=1 \).\( e \)is usually chosen to be a relatively small prime number compared to\( p \)and\( q \)to balance between security requirements and performance. The public key for the party is\( \left(e,\ n\right) \). Calculate\( d \), the modular multiplicative inverse of\( e \)mod\( n \), i.e.,\( d\ \times\ e\ \equiv1\ (mod\ \emptyset\left(n\right)) \)(\( mod\ n \)is equal to the remainder of an integer divided by integer\( n \)).\( \left(d,\ n\right) \)is used as the private key. RSA's security is rooted in the difficulty of factorization of a large number for a classical computer. Any party except for the key generator is not able to obtain\( p \)and\( q \).

In combination with the symmetric key algorithms, the message being encrypted is the symmetric key. RSA protects the symmetric key and ensures this distinct key is shared only between Alice and Bob.

2.3. Digital signatures

The party A generates a public key. How do other parties trust that the key is indeed generated by A? Signatures are signed as a verification of signer's identity. Like signing paper documents with handwritten signature, there are electronic documents with digital signatures. If the party A signs on the electronic documents, it indicates A has known and agreed to its content.

The digital signature process contains three parts [2]. It is utilized to create a digital signature for the electronic documents or messages. It must be secure and not accessible to others, as anyone own this key can imitate as the legitimate owner. The public key is made widely available, enabling everyone to use it to verify the signature. This asymmetric key generation is discussed previously. An example is using RSA to generate the private key\( \left(d,\ n\right) \)and the public key\( \left(e,\ n\right) \).

The second part is the algorithm of generating the signature. The meanings of some symbols are shown in Table 1. The signer computes\( \widetilde{m}=R(m\ ) \), where\( \widetilde{m} \)is an integer within the range\( \left[1,\ n - 1\right] \),\( \widetilde{m}\ \in M_R \)and\( m\in M \).

The last part is the verification of the signature. The verifier obtains the public key\( \left(d,\ n\right) \)from the signer. Then it computes\( \widetilde{m}=\ s^e\ mod\ n \).\( M_{R\ }=\left\{\ R\left(m\right)\right|m\ \in M\} \). The signature is rejected if the verification of\( \widetilde{m}\ \in M_R \)fails. If\( \widetilde{m}\ \in M_R \), then recover the message with\( m=R^{ - 1}(\widetilde{m}) \), where\( R^{ - 1} \)is the inverse of the redundancy function\( R \). In RSA,\( e \)and\( d \)have the property\( ed\ \equiv1\ mod\ n \), so that\( s^e\equiv{\widetilde{m}}^{ed} \)\( \equiv\widetilde{m}\ mod\ n \). This explains why the verification works.

2.4. Hash functions

A hash function is a specific type of algorithm that transforms bit strings of any length into fixed length outputs. It processes a message or a data file as input and produces a result called a hash value, digest, or hash in simple [3]. The hash value is used to represent the message or the data file and depends on the content of the message or the data file [4]. It can be presented as\( h:{{0,\ 1}}^t\ \rightarrow\ {{0,\ 1}}^n,\ m\rightarrow h(m) \).

where\( h \)is the symbol of hash function,\( t \)is an arbitrary finite integer,\( n \)is a fixed integer typically between\( 128 \)and\( 512 \)bits and\( t\text{>}n \). This is a many to one map, indicating that collisions (input pairs with identical output) cannot be avoided. If the mapping is equally distributed, every output is mapped by\( 2^{t - n} \)inputs [5]. The probability of collisions is calculated by\( 2^{t - n}\div2^t=\ 2^{ - n} \). Note that this is solely determined by the size of the hash value. Although the collisions exit, it will take the computer so long time to execute such that the operation is not considered effective within a reasonable timeframe, even with the most powerful computer. This is referred to as computational infeasible. There are three basic properties for the hash function:

This characteristic is also referred to as the one-way property [6]. The preimage resistance is N if the computational work is\( 2^N \). The anticipated preimage resistance of a hash function corresponds to the bit-length of the output. For a hash function with an L-bits output, the security strength is L.

The strength of this resistance is measured by the computational effort needed to have a high probability of finding a second preimage for the hash function..

Notice that this resistance differs from the second preimage resistance as\( x_1 \)is not known. Collision resistance is determined by the amount of computational effort needed to achieve a high likelihood of identifying collisions within a hash function. The anticipated security strength for collision resistance is half the bit-length of the hash output. The security strength is L/2 for an L-bits hash function.

If an application concerns more than one resistance, the weaker strength dominates the security strength. For example, the digital signatures remand both second preimage resistance and collision resistance. In this case, the security strength is described as the collision resistance strength, because the collision resistance strength\( (\sfrac{L}{2}) \)of a hash function is lower than its second preimage resistance strength\( (L) \).

3. Quantum threats

3.1. Quantum computing

Each bit can be either\( 0 \)or\( 1 \). The bits are controlled by physical quantities, for example, the voltage. A low voltage corresponds to\( 0 \)whereas a high voltage represents\( 1 \). The operations of bits follow classical physics rules. In contrast, in quantum computing, quantum bits, or simply qubits, are created and controlled by physical systems that exhibit properties like superposition and entanglement, such as photon spins and trapped ions [7]. Thus, the behaviors of quantum bits are governed by the quantum mechanics of these subatomic particles.

\( \left|\ \varphi\text{>}\ =\ \alpha\right|\emptyset_1\text{>}\ +\ \beta|\emptyset_2\text{>} \)(1)

Where\( \emptyset_1 \)and\( \emptyset_2 \)are the basis states of wave and their inner product is\( 0 \). (1) indicates that, rather than being confined to a certain state, the wave exists as a superposition of two states. A key principle in quantum mechanics is that a system can simultaneously exist in a superposition of several states. An explicit wave function remains unknown until it is measured.

\( \text{<}\vec{u},\ \vec{v}\text{>}\ =\left[u_1,\ u_2\ldots,u_d\right]\left[\begin{matrix}v_1\\\ldots\\v_d\\\end{matrix}\right]=\ {\vec{u}}^T\vec{v} \)(2)

Where\( {\vec{u}}^T \)is the conjugate transpose of\( \vec{u} \). Because\( \text{<}\emptyset_1,\ \emptyset_2\text{>}\ =0 \),\( \emptyset_1 \)and\( \emptyset_2 \)are orthogonal. When the system is measured, it will collapse to state\( |\emptyset_1\text{>} \)with probability\( {|\alpha|}^2 \)or state\( |\emptyset_2\text{>} \)with probability\( {|\beta|}^2 \). Because these are the only two basis states, the total probability must equal\( 1 \):

\( {|\alpha|}^2+{|\beta|}^2=1 \)(3)

This is a fundamental law in quantum mechanics.\( \emptyset_1 \)and\( \emptyset_2 \)are orthogonal and normalized, forming an orthonormal basis in the Hilbert space. Any state in this system is a superposition of these two states and measurement causes the superposition to collapse into one certain state.

The quantum computing takes advantage of superposition and entanglement and manipulate the quantum states with quantum bits. While the classical bits are binary and has only one output in each operation, the quantum bits can process many possible outcomes simultaneously. This is called parallelism.

3.2. Grover's algorithm

It finds a specific item in an unsorted data base of\( N \)items in\( O(\sqrt N) \)[8]. The problem is:

Given:\( f:\ {{0,\ 1}}^n\ \rightarrow\left\{0,1\right\} \), find the bit string\( w \)such that\( f\left(w\right)=1 \). The existence of\( w \)is guaranteed.

In classical algorithms, the length of the input is\( N=\ 2^n \). One needs to loop through the sequence of input and calculate\( f \)one by one until finding\( w \). The time complexity of classical algorithm is\( \mathcal{O}(N/M) \), provided that there are\( M \)solutions precisely, i.e.,\( M=|\left\{x:f\left(x\right)=1\right\}| \)[9].

Grover's algorithm contains two key components: An oracle that flips the phase of the target state and a phase operation that amplifies the likelihood of measuring this desired state. The oracle evaluates the state and flips the phase if the solution is found, and the solution is then enhanced by the second oracle.

3.3. Shor's algorithm

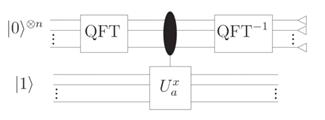
Figure 1. The circuit implementation of Shor's algorithm (Photo credit: Original).

As show in the figure 1. The problem is: given\( N=pq \)for some unknown\( p,q \)such that\( \gcd{\left(p,q\right)}=1, \)find\( p \)and\( q \).

In modular arithmetic, the remainder of\( a^x \)divided by\( N \)is periodic, allowing the factorization problem to be transformed into an ordering-finding problem. This can be effectively solved using quantum algorithms.

This transforms the superposition of states to an approximate superposition of periods. Upon measurement, the system collapses to an estimate related to the period. The possibility of finding the period is amplified by QFT.

The time complexity for determining the order of a random element in\( Z_n^\ast \), i.e.,\( Z_n^\ast={k\in\mathbb{Z}|1\le k\text{<}n\ and\gcd{\left(k,\ n\right)}=1} \)with the quantum algorithms is\( \mathcal{O}(\left(logN\right)^2loglog\left(N\right)logloglog\left(N\right)) \), which is a polynomial of\( log\left(N\right) \). Compared to the classical algorithms that has a time-complexity of\( e^{\mathcal{O}\sqrt{logNloglogN}} \), Shor's algorithm speeds up the factorization exponentially.

3.4. Security assessment

Table 2. Examples of widely deployed cryptographic systems and their conjectured security levels.

Table 2 shows that the security levels against attacks with pre-quantum algorithms verses post-quantum algorithms.

Grover's algorithm directly targets this problem by speeding up the brute-forcing attack quadratically. Grover's algorithm, as is depicted in Figure 2, reduces the attack time against AES-\( n \)from\( 2^n \)operations to\( 2^{n/2} \)operations, halving the security level. Implementing Grover's algorithm in practice demands a large amount of resources and cost, making it currently impractical for real-world attacks. For AES-\( 128 \), it is estimated to evolve\( 3000 \)to\( 7000 \)logical qubits and\( 1000 \)to\( 2000 \)quantum gates per phase flip operation [10].

In contrast, the security of information encoded via asymmetric key algorithms like RSA rests on the computational infeasibility of prime factorization of large numbers using classical computers.

4. Migration to Post-Quantum cryptography

4.1. Start the migration now

Businesses and organizations must guarantee that their sensitive data, e.g., national security documents, medical records and trade secrets, that are encrypted using traditional cryptography, stays indecipherable for many years; Moreover, there are long-lifespan projects including vehicles, infrastructures, etc., that lives from the pre-quantum era to post-quantum era; Besides, the transition to PQC takes a long time. It contains both hardware and software transitions.

4.2. NIST's standardization

Figure 2. The timeline of PQC competition arranged by NIST [11].

As show in the figure 2. The standardization of PQC ensures security and efficiency of the migration. Institutes rigorously decide the most robust algorithms for secure communication among systems. Standardization provides organizations a clearer path of migration.

It has approved standardization of XMSS and LMS schemes, which are both stateful hash-based signature schemes. It has also standardized some symmetric key scheme. Right now, NIST is working on public key PQC algorithms.

NIST also receives comments from the public. In\( 2020 \), NIST selected fifteen candidates for the third-round scheme. Seven of them were chosen to be ‘finalists', while the others are labelled as ‘alternatives'. NIST considered the finalist algorithms to be the most compromising to fit most common cases. The set of elements in the alternatives are potential candidates for further standardization, probably in the next round of scheme. Among\( 9 \)algorithms in the finalists, there are\( 5 \)KEMs and\( 4 \)digital signature schemes.

The algorithms are CRYSTAL-KYBER (KEM), CRYSTAL-Dilithium (digital signature) and SPINCS+ (digital signature). The three standards are designed with future security in mind, and NIST is urging system administrators to start adopting these new standards without delay.

5. Conclusion

This paper has thoroughly examined the exigent shift required from traditional cryptographic systems to Post-Quantum Cryptography (PQC) due to the evolving quantum threat landscape. We have highlighted the vulnerabilities exposed by advanced quantum algorithms such as Shor's and Grover's, which threaten to compromise current encryption methods that are foundational to securing sensitive digital communications. The discussion detailed the current efforts led by the National Institute of Standards and Technology (NIST) in establishing a standardized approach towards adopting robust PQC solutions. These efforts are crucial to not only mitigating the risks posed by quantum computing capabilities but also in setting a proactive pathway for future cryptographic applications. Moreover, the paper analyzed both the technical and organizational challenges inherent in the transition process, emphasizing the need for a structured migration strategy that aligns with NIST's standards to ensure seamless integration and security continuity. Directions for Future Research: Looking forward, the field of quantum-resistant cryptography must focus on several key areas to further bolster the security of digital systems. Future research should aim to develop more efficient and scalable PQC algorithms that can be seamlessly integrated into existing infrastructure with minimal disruption. There is also a pressing need to explore more advanced cryptographic protocols that can operate effectively under the constraints of both current and emerging quantum technologies. Additionally, further studies should investigate the long-term implications of quantum computing on data privacy and security, particularly in sectors where highly sensitive information is routinely processed, such as healthcare, finance, and national security.