1 Introduction

PID controllers play an important role in industrial control and automation systems [1]. As a classical control strategy, PID controller can stabilize the system and optimize its dynamic performance by adjusting three parameters of the controller (proportional gain Kp, integral time constant Ki, and differential time constant Kd) [2]. Especially in robot dynamics, PID controller is widely used in motion control, path tracking and attitude control. However, robot dynamics systems tend to be highly nonlinear and coupled, greatly affected by external perturbations, and more sensitive to changes in system parameters [3]. This complexity makes the traditional PID control often show insufficient performance when dealing with multi-variable and nonlinear systems, such as slow response speed, large steady-state error and poor robustness [4][5][6]. Therefore, to improve the performance of the control system, the optimization of PID controller parameters is particularly important. In order to solve the above problems, this paper aims to optimize the parameters of the PID controller by using the particle swarm optimization (PSO) algorithm to improve the control performance of robot dynamics system.

2 Method

2.1 Experimental scheme design

The purpose of this paper is to automatically adjust the parameters of the PID controller by using the particle swarm optimization (PSO) algorithm to improve its control performance in complex dynamic systems [7]. PSO algorithm is an optimization technique based on swarm intelligence, which is inspired by the foraging behavior of birds. It can effectively search for the global optimal solution in multidimensional space and is suitable for solving the complex problem of PID parameter optimization, which is multi-peak and multi-variable [8]. This study will verify the significant improvement of PSO-optimized PID controllers in control accuracy, response speed and steady-state performance through simulation experiments, and compare and analyze with traditional unoptimized PID controllers.

2.2 Simulation experiment

Based on PSO algorithm, the simulation experiment of PID controller parameter optimization is carried out by MATLAB. The simulation system adopts a second-order transfer function representing the dynamics of the mobile robot [9]:

\( G(s)=\frac{K∙ω_{n}^{2}}{s^{2}+2ζω_{n}S+ω_{n}^{2}} \) (1)

In this equation, K is the system gain, \( ω_{n} \) is the system's natural frequency, and ζ is the damping ratio. The transfer function can well simulate the robot system's dynamic response.

In the simulation experiment, the parameters of PID controller are randomly initialized and iteratively optimized by PSO algorithm. The initialization of a particle swarm consists of 30 particles, each representing a set of PID parameters (Kp, Ki, Kd). Through 100 iterations, the algorithm gradually adjusts the position and velocity of the particle to find the optimal PID parameter combination.

\( C(s)=K_{p}+\frac{K_{i}}{s}+K_{d}∙s \) (2)

In each iteration, the algorithm computes the system response curve for the PID parameter corresponding to the current particle and evaluates its performance by integrating absolute error (IAE).A smaller IAE indicates that the response of the system is closer to the ideal output and the control performance is better [10]. The experimental results show that the PID parameters after PSO optimization are significantly better than the parameters before optimization, which indicates that PSO algorithm has good application potential in PID control optimization.

In this simulation experiment, IAE and ISE were selected as the main performance indicators because they can comprehensively evaluate the controller's ability to minimize errors in the whole response process [11].

\( IAE=\int_{0}^{T}|r(t)-y(t)|dt \)

\( ISE=\int_{0}^{T}(r(t)-y(t))^{2}dt \) (3)

2.3 Analysis of optimal PID algorithm under the condition of multivariable and nonlinear system control performance

Simulation experiment results:

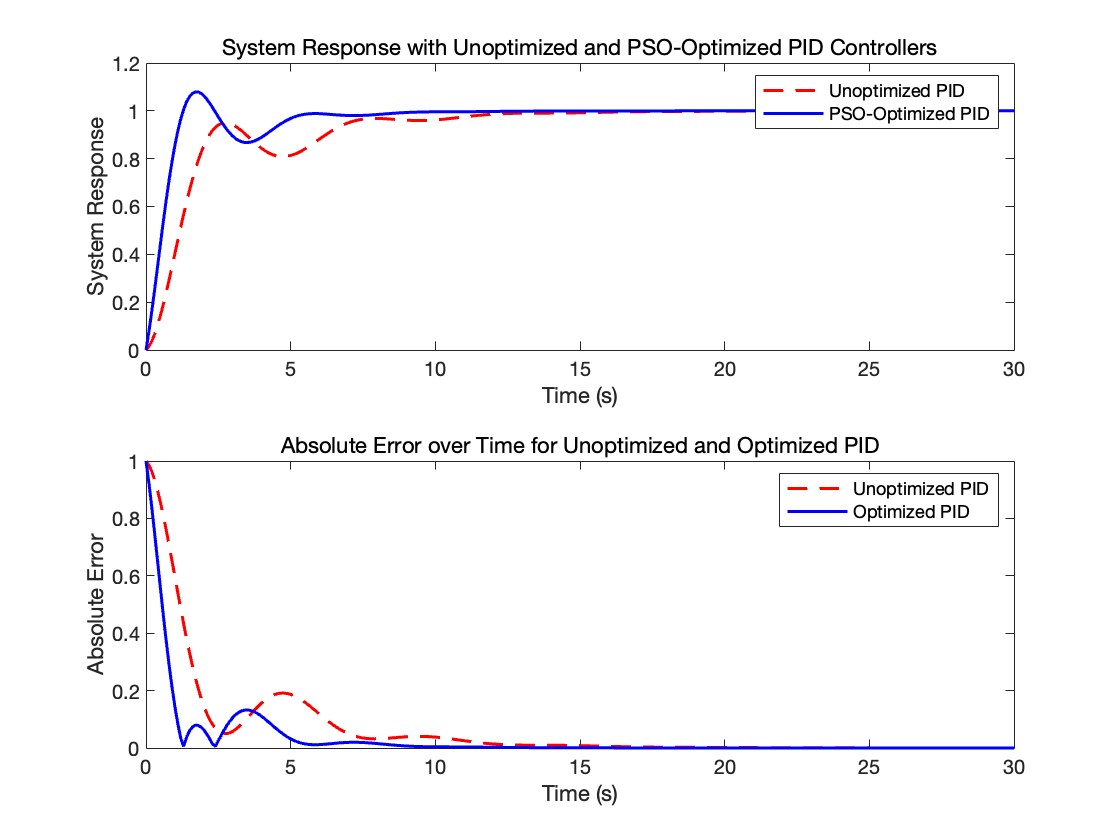
Figure 1a. System Response speed comparison diagram.

As shown in Figure 1 a, the performance of the PID controller before and after optimization can be compared and analyzed, and the effect of PSO optimization on improving system response speed and accuracy can be clearly seen.

In Figure 1 a, a comparison of system response speed, control accuracy, and steady-state performance is shown. First of all, from the perspective of response speed, the unoptimized PID controller (red dotted line) shows a slow response speed, the system takes a longer time to stabilize, and there is obvious oscillation after the initial step input, indicating that the system needs a longer time to reach the expected output. The PSO-optimized PID controller (solid blue line) showed a faster response, with the system reaching the desired output quickly and oscillations reduced, indicating a shorter rise time and a more agile response to input changes. Secondly, from the perspective of control accuracy, the unoptimized PID controller overshoots greatly during the initial response, and the oscillation amplitude is obvious, and it is difficult to maintain the output close to the set point. The PSO-optimized PID controller has higher control accuracy, reduced overshoot, and reduced oscillation amplitude, and the system is able to closely track the desired output from the beginning and maintain a more accurate response throughout the transient phase. Finally, analysis of steady-state performance shows that unoptimized PID controllers take longer to maintain a steady state, and the oscillation duration is longer, resulting in greater steady-state errors. The steady-state performance of PSO-optimized PID controller is better, and the system not only reaches steady-state faster, but also can maintain the expected output with minimal error, indicating that the optimized controller successfully eliminates steady-state error and can achieve fast and accurate output.

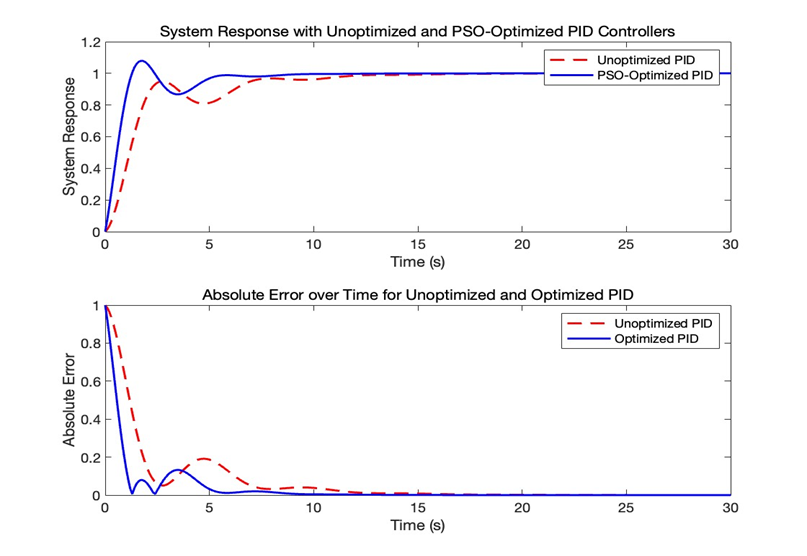
Figure 1b. AE vs. Time comparison diagram.

In Figure 1 b, the performance of the controller before and after optimization can be analyzed in the following aspects. First of all, the initial SE values of both controllers are high, close to 1, indicating a large initial error. Subsequently, the error of both controllers dropped rapidly in the first few seconds, but the optimized PID controller reduced the error faster and showed better dynamic response. In terms of steady-state behavior, the error of the PSO-PID controller tends to stabilize earlier, approaching zero in about 5 seconds, while the unoptimized PID controller takes a longer time to reach stability, and shows poor steady-state performance with certain oscillations during the period. Finally, from the perspective of overall performance, the optimized PID controller has a lower SE in the whole process, indicating that its error minimization effect is better and the area under the SE curve is smaller, which further verifies the advantages of the optimized PID controller in control accuracy and response speed.

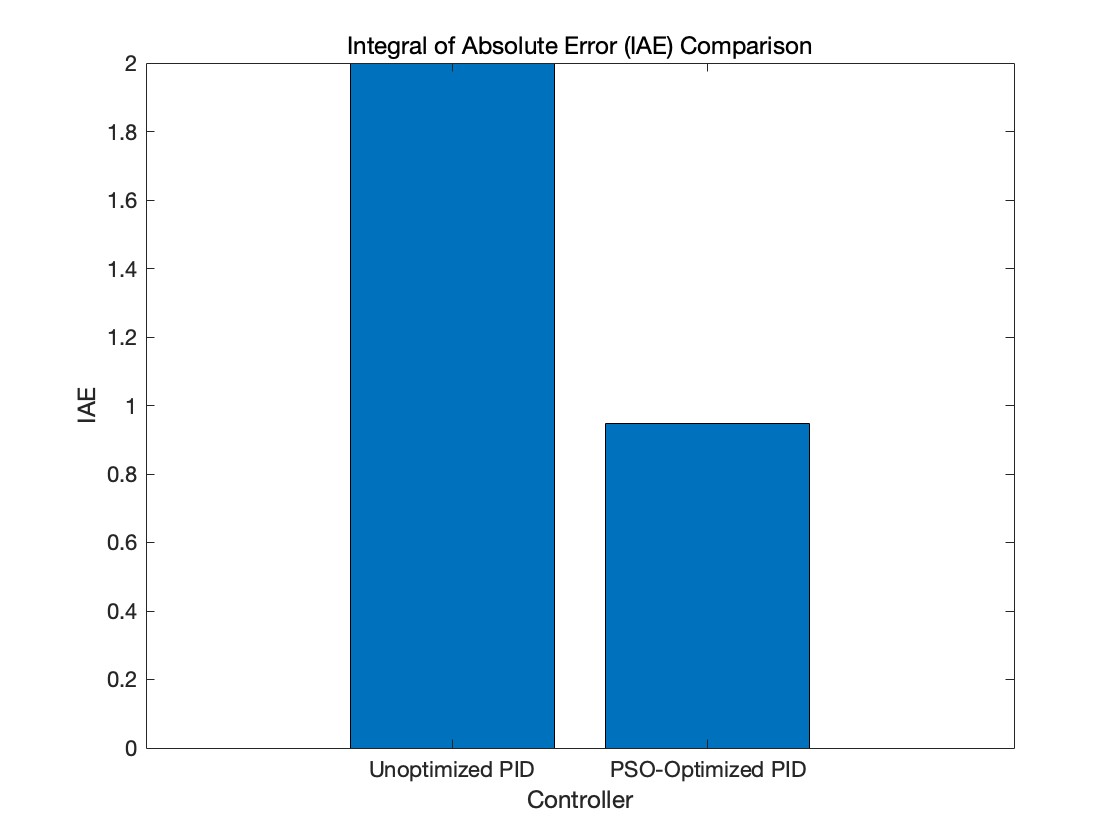
Figure 2. IAE integration comparison diagram.

Figure 2 by a comparison of the two controllers IAE integral further confirmed these findings. The IAE integral quantifies the error accumulated over time. For PSO-optimized PID controllers, the IAE integral is significantly smaller, indicating that the control system is more accurate and efficient. This result clearly validates the effectiveness of using PSO to enhance PID controller performance in complex dynamic systems.

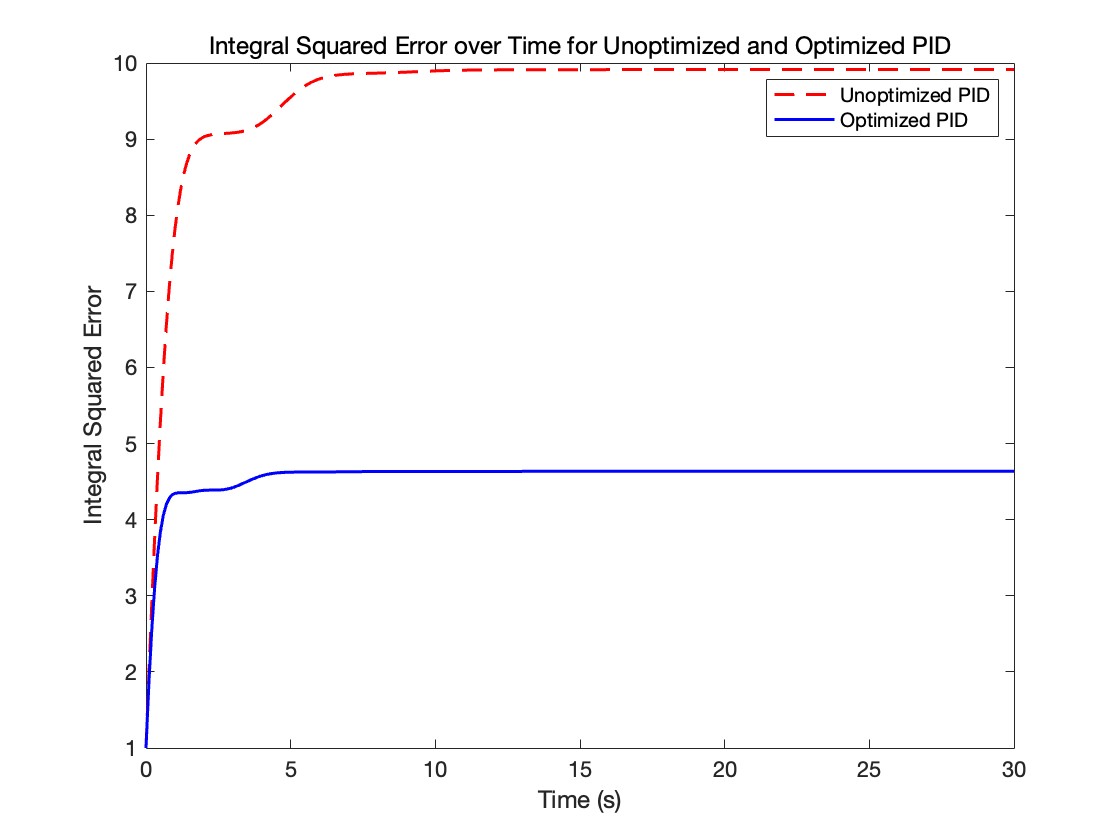
Figure 3. ISE comparison diagram.

As shown in Figure 3, the ISE of the unoptimized PID controller increases rapidly in the initial phase and finally stabilizes at about 10. Such a high ISE value indicates that the system has accumulated significant errors over time, indicating that the performance of the unoptimized PID controller is poor. The PSO-PID starts out with a low ISE value and quickly stabilizes around 4.5. This shows that after optimization, the error is obviously reduced and the efficiency of the control system is significantly improved. The optimized PID controller is obviously better than the unoptimized one. Not only is the ISE value lower, but it also stabilizes faster. This means that the responsiveness and accuracy of the system are improved through optimized PID parameter adjustment.

In summary, the PSO optimization algorithm performs well when dealing with multivariable and nonlinear control systems, not only speeding up the response speed of the system but also improving the control accuracy and steady-state performance. These improvements are important for improving the robustness and adaptability of the robot's dynamic control system.

3 Conclusion

This experiment proves the effectiveness of the PSO algorithm in PID controller parameter optimization through simulation experiments. For mobile robot systems with complex dynamic characteristics, traditional PID controllers are often difficult to provide an ideal control effect. By introducing PSO optimization technology, the dynamic response speed, control accuracy and steady-state performance of the system can be significantly improved, so as to meet higher control requirements.

The results show that PSO-optimized PID controller has significant advantages in dealing with nonlinear and multivariable control problems. This optimization strategy is not only applicable to mobile robots, but also can be extended to other complex control systems, such as drones and autonomous vehicles. In addition, the fusion of the PSO algorithm and other advanced optimization algorithms has a broad prospect. In the future, we can try to combine PSO with machine learning, deep learning, and other adaptive technologies to achieve automatic tuning and real-time optimization of the controller, so as to improve the intelligence level of the system. In addition, the extended application of the PSO optimization algorithm is not limited to the field of robotics, but can also be applied to the optimization control of automated production lines, intelligent transportation systems, and complex energy systems in the context of Industry 4.0. Through further research and practical application, PSO optimization technology is expected to become one of the core tools of intelligent control systems and promote the innovation and breakthrough of modern control technology.