1. Introduction

In the realm of contemporary industrial and service robotics, trajectory tracking control is a crucial research topic. When performing complex tasks, robots must move precisely along a predetermined trajectory to ensure the successful completion of the task. However, trajectory tracking control faces many challenges due to the nonlinearity, uncertainty and external interference of the robot system [1]. Sliding Mode Control (SMC), known for its robustness and superior anti-interference capabilities, is widely employed in the management of robot trajectory tracking.

Current methods for robot trajectory tracking control encompass proportional-integral-derivative (PID) control, adaptive control, fuzzy control, and more [2]. These methods solve the trajectory tracking problem to a certain extent, but their effectiveness is limited when faced with nonlinearity, uncertainty, and external disturbances. Although PID control is widely used, it cannot compensate for inertia changes and coupling torque, so it is difficult to adapt to changing payloads and high-speed operation. Although adaptive controls can handle uncertainties in robot kinematics and dynamics, they usually require complex implementations and may have difficulty dealing with non-holonomic constraints [3]. in addition, traditional fuzzy controllers have limitations, including steady-state errors and parameter optimization challenges [4-5], and therefore cannot meet the increasing complexity and accuracy requirements of control systems alone.

SMC is a control strategy that stands out because of its resilience to variations in system parameters and its ability to counter external disturbances [6]. Traditional SMC reaches its objectives by constructing a sliding surface and implementing switching control laws, ensuring the system state glides along this surface. However, traditional SMC has the problem of high-frequency jitter, which not only impacts control accuracy but also potentially harms the actuator. To solve this problem, researchers have proposed a variety of improved methods, including integral sliding mode control (ISMC) [7] and adaptive neural network sliding mode control (ANNSMC).

ISMC improves system robustness and dynamic performance by incorporating integral terms into the sliding framework, effectively reducing the high-frequency oscillations phenomenon. ANNSMC combines the self-learning ability of neural networks with the robustness of SMC, realizes online adaptive adjustment of control parameters, and further improves the adaptability and control accuracy of the system.

The objective of this study is to explore the utilization and impact of SMC on the accuracy and efficiency of robot trajectory tracking. This paper will review the application of traditional SMC, ISMC and ANNSMC in robot trajectory tracking control, assess the strengths and weaknesses of each method and evaluate their real-world applications. This paper will first introduce the basic principles and mathematical models of SMC, then analyze the main technical difficulties faced throughout robot trajectory tracking, and then evaluate the application effects of traditional SMC, ISMC and ANNSMC in different robot systems through specific cases. Finally, it summarizes the shortcomings of current SMC in robot trajectory tracking and proposes future research directions.

Through in-depth research on SMC and its improvement methods, I hope to provide more effective solutions for robot trajectory tracking control and promote the further development of robotics in various fields. The robustness and anti-interference ability of SMC enable it to perform well in complex environments, while the introduction of ISMC and ANNSMC further improves the dynamic performance and adaptability of the system, providing new ideas and methods for achieving high-precision trajectory tracking.

2. Sliding mode control principle

The core concept behind SMC is to reach the control objective by designing a sliding surface, ensuring the system state glides along it. Typically, designing a sliding mode controller involves two crucial steps: crafting the sliding layer and formulating the control strategy.

2.1. Sliding surface design

The sliding surface is typically formulated as a linear blend of state variables, expressed as:

\( s(x)=Cx\ \ \ (1) \)

Where s(x) is the sliding layer, C is the structural matrix, x is the system state vector.

In a standard second-order system, the sliding layer can be constructed as:

\( s(x)=\dot{e}+λⅇ\ \ \ (2) \)

Where \( e={x_{d}}-x \) is the tracking discrepancy, \( λ \) is a positive factor, \( {x_{d}} \) is the desired trajectory.

Designing the sliding layer must satisfy the attainment criterion, which is:

\( \dot{s(x)}=0\ \ \ (3) \)

This ensures that the system status can attain the sliding layer and remain there within a finite period.

The key to sliding layer design is to select appropriate parameter \( λ \) so that the system demonstrates strong dynamic performance and robustness while on the sliding surface. Usually, the selection of parameter \( λ \) can be determined by experiments or optimization algorithms.

2.2. Control law design

The SMC law is crafted to guarantee that the system state swiftly reaches and maintains its position on the sliding surface. Common control law forms are:

\( u={u_{eq}}+{u_{sw}}\ \ \ (4) \)

Where \( {u_{eq}} \) is equivalent control and \( {u_{sw}} \) is toggle control.

Equivalent control ensures the system stays on the sliding layer and is designed using the system's nominal model. In the context of a second-order system, the expression for equivalent control is:

\( {u_{eq}}=\frac{1}{b}(x_{d}^{n}-αx-λ\dot{e})\ \ \ (5) \)

Where \( α \) and \( b \) are system parameters.

Toggle control is employed to guide the system state toward the sliding layer, and its design is based on the sign function of the sliding layer. Common toggle control forms are:

\( {u_{sw}}=-ksign(s(x))\ \ \ (6) \)

Where \( k \) is a positive parameter and \( sign(s(x)) \) is the sign function of the sliding layer.

To mitigate quick oscillatory phenomenon, continuous switching control can be used, with techniques like saturation or power functions:

\( {u_{sw}}=-k\frac{s(x)}{|s(x)|+ε}\ \ \ (7) \)

Where \( ε \) is a small positive constant.

3. Classification of sliding mode control in robot trajectory tracking control

The technical difficulties faced by robot trajectory tracking control significantly affect its performance and reliability.

First, model uncertainty is a core issue in trajectory tracking, affecting all aspects of the process [8]. Robot systems often have complex dynamic characteristics, which are affected by factors such as parameter changes, wear and external environment, resulting in differences between the preset model and the actual behavior. Second, external disturbances, including unexpected external forces, friction changes and load fluctuations, further increase the control difficulty of trajectory tracking [9]. Underactuation issues frequently occur in robotic systems, particularly when there are fewer control inputs than the number of independent parameters within the system. This not only makes the design and adjustment of the control system more complicated, but also may reduce the system's ability to suppress disturbances [10]. For example, in an underactuated robot arm, some joints may not be able to be driven directly and need to be controlled through the coupled motion of other joints, which increases the difficulty of achieving accurate trajectory tracking. In addition, despite SMC widespread use in robot trajectory tracking for its robust performance, its switching logic may induce high-frequency chattering [11]. This chattering not only excites unmodeled dynamic responses, increases system wear and energy consumption, but also may cause actuator fatigue and system instability, which in turn impacts the precision and stability of trajectory tracking [12].

To address the above challenges, researchers and engineers are constantly exploring and developing advanced control strategies. Although traditional S is favored for its robustness, its inherent high-frequency chattering problem has stimulated the pursuit of improved algorithms. Integral sliding mode control (ISMC) came into being. By introducing an integral link, it not only effectively alleviates the chattering phenomenon, but also ensures that the robustness of the system is maintained [13]. At the same time, adaptive neural network sliding mode control (ANNSMC) represents another innovative direction. It combines the self-learning ability of neural networks with the toughness of SMC, and can intelligently adjust the controller parameters to adapt to the nonlinearity and uncertainty of the robot system [14].

3.1. Traditional Sliding Mode Control (SMC)

Traditional sliding mode control (SMC) is recognized for its robust performance in managing variations in system variables and mitigating external perturbations. This stems from the formulation of its switching control law, which can effectively handle unpredict abilities and interferences, while maintaining system state stability on the sliding mode surface. Simultaneously, SMC demonstrates rapid response abilities, ensuring the system swiftly reaches its desired state. In addition, its implementation process is relatively simple, primarily encompassing the creation of suitable sliding mode surfaces and the application of switching control laws. Nonetheless, SMC also presents some challenges. High-frequency chattering is a significant problem, which results from high-frequency switching of the control law, resulting in swift oscillations near the slip surface. In addition, under certain circumstances, SMC may cause an overshoot phenomenon, that is, the system state exceeds the expected value and then returns again. Simultaneously, designing the parameters for a sliding mode controller is intricate, necessitating a thorough understanding of the system's dynamic characteristics and inherent uncertainties. These problems need to be paid attention to and solved in practical applications.

SMC has been effectively utilized across a spectrum of robotic systems, such as skid-steer mobile robots [15] and wheeled mobile robots [16].

Muhammed Alhelou and his team thoroughly investigated the trajectory following issues of a skid-steering mobile robot. They proposed two distinct dynamic modeling strategies and evaluated their respective performances (Figure 1). This research highlighted the potential of SMC in tracking the trajectory of skid-steering mobile robots and emphasized the importance of conventional SMC in robot trajectory tracking control applications, especially in the face of complex dynamic environments and bounded disturbances.

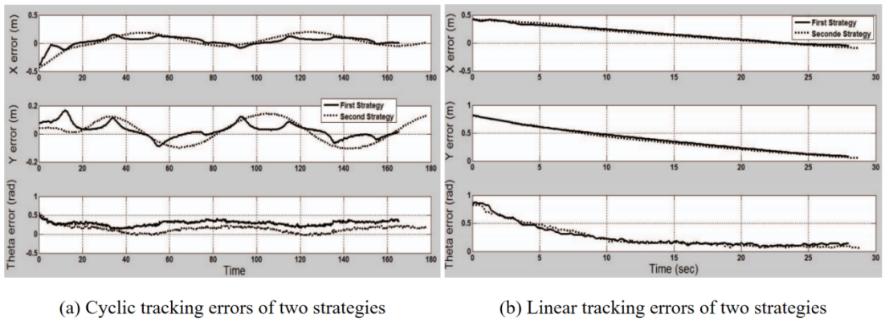
Figure 1. Comparative analysis of tracking errors in different strategies [15].

In the concluding segment of Razvan Solea et al.'s investigation into trajectory tracking control for wheeled mobile robots, real-time tests verified the effectiveness of the proposed control strategy. The PatrolBot mobile robot was utilized for a series of experiments and the findings indicated that the suggested control approach could successfully track the predefined trajectory across various mass conditions. The experimental data showed that the lateral, longitudinal and directional errors all tended to zero, proving the robustness of the method in the face of mass changes.

These studies demonstrate the effectiveness of SMC in achieving asymptotic stability of tracking errors for various trajectories, including circular and linear paths. Experimental results show improved convergence speed, tracking accuracy, and resilience against parameter instabilities and environmental disruptions. The versatility of SMC is reflected in its application in kinematic and dynamic models of mobile robots, making it a valuable control strategy for robot trajectory tracking. However, SMC may be limited under high-precision control requirements due to high-frequency jitter problems, which require filters or other methods to reduce the effects of jitter.

3.2. Integral Sliding Mode Control (ISMC)

Integral sliding mode control (ISMC) has become a stable technology for mobile robot trajectory tracking. By incorporating the integral term into the sliding plane, ISMC is proficient in minimizing the system's steady-state deviation and enhancing control precision. The introduction of the integral term enables the control system to compensate for the accumulated error, thereby reducing the error in the steady state. This approach is especially apt for high-precision control systems, as it markedly enhances control performance without adding to system complexity.

In addition, ISMC alleviates the high-frequency chattering problem to a certain extent. High-frequency chattering, often stemming from the rapid switching of control inputs, is a prevalent issue in SMC. By introducing the integral term, the change of the control input becomes smoother, thereby reducing the impact of high-frequency chattering. This not only improves the stability of the system, but also extends the service life of the actuator.

In the trajectory tracking control of mobile robots, ISMC can greatly enhance the system's steady-state accuracy and effectively counteract external disturbances [17]. For example, in mobile robot navigation, external disturbances such as uneven ground, wind, etc. can cause the robot to deviate from the predetermined path. Although traditional SMC can cope with these disturbances, it may have certain errors in the steady state. Introducing ISMC enhances the system's ability to compensate for disturbances, thereby boosting the accuracy of path tracking. In addition, ISMC is also used to solve the trajectory tracking complication of wheel-based mobile robots under conditions of uncertainty. The results show that this method can eliminate the arrival stage that cannot be solved by SMC and minimize the mismatch interference problem, improving the robustness and tracking accuracy of the system [18]. It can be seen that ISMC shows strong robustness in practical applications, even under challenging conditions such as payload changes and friction [17], and therefore can effectively cope with the operation of robotic arms in complex environments. various disturbances and uncertainties.

3.3. Adaptive Neural Network Sliding Mode Control (ANNSMC)

Adaptive neural network sliding mode control (ANNSMC) was proposed to address the limitations of traditional SMC, which is able to eliminate jitter and compensate for uncertainty without needing prior system knowledge [19]. ANNSMC combines the nonlinear mapping prowess of neural networks with the resilience of SMC, ensuring effective management of variabilities and external perturbations in robot trajectory tracking. In mobile robot trajectory tracking, ANNSMC uses neural networks to perform real-time estimation and compensation for system uncertainties, thereby improving the accuracy of trajectory tracking [20]. For example, Thanh Nguyen Truong and others applied the new ANNSMC algorithm that combines integral SMC, radial basis function (RBF) neural network and adaptive technology to a three-degree-of-freedom parallel manipulator to improve its accuracy, reduce jitter and speed up the convergence speed. The simulation outcomes reveal (Figure 2), Compared with traditional SMC, the newly proposed control strategy shows significant advantages in tracking accuracy and fast convergence. The designed controller can approach the desired trajectory more quickly, and the chattering in the control signal is notably diminished [21]. In addition, Xingmin Fan's team devised an adaptive sliding mode controller leveraging an RBF neural network to enhance the trajectory tracking control of mobile robots. Experimental outcomes indicate that this method effectively handles system variabilities and external perturbations, and significantly improve the accuracy of trajectory tracking [22]. In space robot trajectory tracking control, ANNSMC addresses system dynamic uncertainties and environmental disturbances. By employing the RBF neural network to estimate uncertainty terms, in conjunction with a terminal sliding mode controller devoid of singularities, the researchers achieved stable control and trajectory tracking of the space robot system. Simulation outcomes indicate that this method excels in error convergence speed and control accuracy [23]. In controlling the trajectory of a manipulator, ANNSMC approximates the nonlinearity and uncertainty in the system through the neural network, and eliminates the approximation error through the sliding mode controller. Wang Song's team introduced an enhanced ANNSMC, leveraging the particle swarm optimization algorithm to fine-tune the neural network's structural parameters, thereby minimizing chattering. Based on experimental outcomes, the method demonstrates significant enhancements in both control accuracy and robustness [24]. These examples demonstrate the wide application and significant effects of ANNSMC in trajectory tracking of the proposed robot, especially its advantages in coping with uncertainty and improving control accuracy.

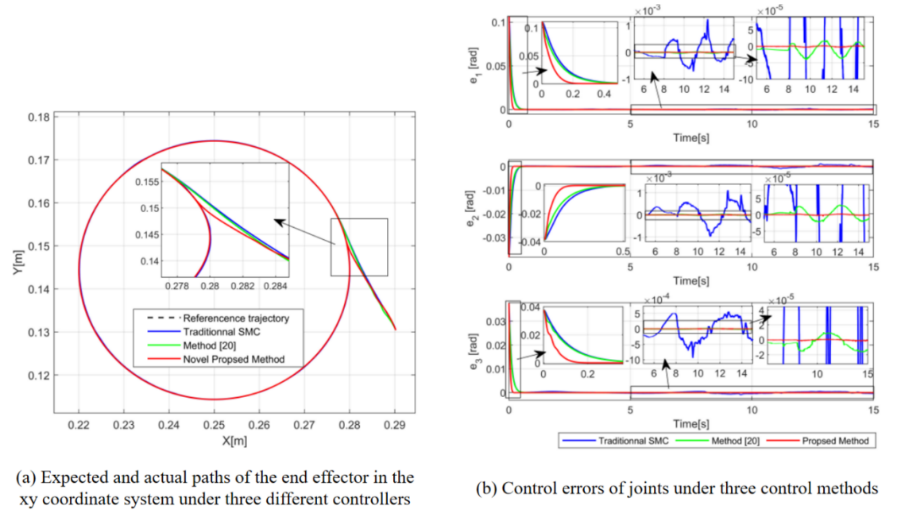
Figure 2. Analysis of end effector path and joint control error under three control methods [21].

4. Conclusion

In summary, the application of SMC in robot trajectory tracking has evolved from SMC to ISMC and then to ANNSMC. Each method solves the system chattering problem to varying degrees and improves trajectory tracking accuracy and stability. However, SMC still has problems such as high-frequency chattering, design complexity, and lack of robustness in robot trajectory tracking.

Future research can further explore how to combine different control strategies to deal with disturbances and uncertainties in more complex practical application scenarios. For example, it is possible to consider combining SMC with other advanced control methods (such as fuzzy control, predictive control, etc.) to design a more intelligent and efficient control system to meet the high precision and high reliability requirements of robotic arms in industrial, medical and other fields. In addition, research on more effective vibration suppression methods and their application in multi-robot systems will also be an important direction in the future. Through these improvements, the application of SMC in robot trajectory tracking will be more extensive and in-depth.