1. Introduction

Bipartite graphs, a fundamental concept in graph theory, are widely used in various fields such as computer science, biology, and social sciences. These graphs consist of two disjoint sets of vertices, where each edge connects a vertex from one set to a vertex in the other set. Applications of bipartite graphs include modeling relationships between two different types of entities, such as students and courses, users and items, or computers and networks. They simplify many computational problems, including matching, assignment, and scheduling, making them invaluable in areas like web search engines, social networks, and data mining​. This paper delves into algorithms related to bipartite graphs, specifically focusing on the Depth-First Search (DFS) algorithm and its applications. The primary objectives are to: Discuss the use of DFS in determining whether a graph is bipartite through the graph coloring algorithm. Explain the Hungarian algorithm for finding the maximum matching in bipartite graphs.

The study employs both literature research and experimental methods. Literature research involves reviewing existing studies and algorithms related to bipartite graphs. The experimental method includes implementing the discussed algorithms in C++ to demonstrate their practical applications and effectiveness.

Understanding and applying algorithms for bipartite graphs is crucial for solving complex problems in various domains. This research lays the groundwork for further exploration and innovation in graph theory and its applications, potentially leading to more efficient algorithms and solutions in computer science and related fields.

2. Depth-First Search and Concept of Bipartite Graphs

Definition of backtracking and common steps of backtracking. The backtracking algorithm is a search attempt process similar to enumeration, mainly in the search attempt to find a solution to the problem, when it is found that the solution conditions are not satisfied, it is "backtracking" back to try another path. Backtracking is a kind of optimal search method, which searches forward according to optimal conditions to reach the goal. However, when the exploration reaches a certain step, it is found that the original choice is not optimal or does not reach the goal, and it is taken back a step to choose again [1].

2.1. Common steps of backtracking

Determine the solution domain of the given problem

Determine the extended search rules for the node

Traverse the solution domain (pruning function can be used to appropriately avoid invalid searches)

Depth-First Search (DFS) algorithm

Depth-First Search (DFS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. It traverses a graph or tree as deeply as possible along each branch and uses a stack to remember the next vertex to visit. The algorithm begins at the root node and explores as far as possible along each branch before backtracking. If the condition is not found to be satisfied during the traversal, backtracking is performed [2] [3].

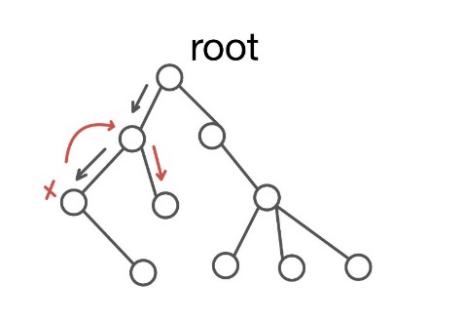
Figure 1: Example of backtracking

For example, in this graph above, we take the top node as the root, and then we will explore as far as possible along each branch when the conditions are satisfied. If the condition is not satisfied, it returns to the previous node to continue searching for another path [4][5].

Then we need to understand the concept of bipartite graphs. In discrete mathematics, a bipartite graph is a special type of graph in which the vertices can be divided into two disjoint sets, and every edge connects a vertex from the first set to a vertex in the second set. In other words, if you partition the set of vertices into two parts, then every edge has one endpoint in each part.

Bipartite graphs have many applications in various fields, including computer science, biology, social sciences, and operations research. They are commonly used to model relationships between two different types of entities, such as students and courses, users and items, or computers and networks. The bipartite structure of these graphs simplifies many computational problems, such as matching, assignment, and scheduling [6][7].

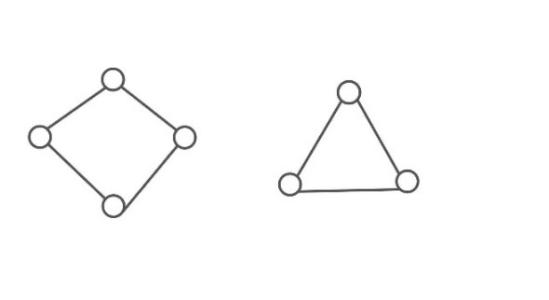
Figure 2: Examples of a bipartite graph and non-bipartite graph

There is a very simple example of what is a bipartite graph and what is a non-bipartite graph. The left graph is bipartite, because we can divide all vertices into two sets and there are only edges between the two sets, and no edges within the set. However, for the right graph, there is no way to make the two sets separated without edges within both sets.

3. Judgment of Bipartite Graph: Graph Coloring Algorithm

The method of determining whether a graph is a bipartite graph is often referred to as the "Coloring Algorithm". In this method, each vertex of the graph is assigned a color in such a way that no two adjacent vertices have the same color. If such a coloring is possible, then the graph is bipartite; otherwise, it is not. This method is based on the concept of bipartite graphs, which are graphs whose vertices can be divided into two disjoint sets such that no two vertices within the same set are adjacent [8][9].

3.1. Realization

·Start with an arbitrary vertex and assign it a color

·Color all of its neighbors with the opposite color

·Repeat this process for all vertices, ensuring that each vertex is assigned a color different from its neighbors

·If at any point it becomes impossible to assign colors to vertices without violating the condition that no two adjacent vertices have the same color, then the graph is not bipartite

·If all vertices can be colored without conflict, then the graph is bipartite

3.2. C++ implementation code

In this algorithm, we use 1 and 2 to represent the two different colors, assuming that a point is colored as c, then all points adjacent to it should be the color 3-c. For each point, we use a depth-first search to search. For vertex u, we color it as c, then we traverse the points that are adjacent to u, if the adjacent point has no color, then the point is colored as 3-c, recursively processed. If it was already colored, determine whether the color is 3-c. If we traverse the whole graph and don't find a contradiction, then return true, which means the graph is bipartite.

bool dfs(int u, int c)

{

color[u] = c; //color vertice u

for (int i = h[u]; i != -1; i = ne[i]) //traverse the points that are adjacent to u

{

int j = e[i];

if (!color[j]) //if the adjacent point has no color, then the point is recursively processed.

{

if (!dfs(j, 3 - c)) return false; //if c=1,then 3-c=2

//if c=2,then 3-c=1

}

else if (color[j] == c) return false;

//if it was already colored, determine whether the color is 3-c

}

return true;

}

The coloring method provides a practical way to determine whether a given graph is bipartite without having to exhaustively search for the presence of odd cycles, which is another characteristic of bipartite graphs. Instead, it relies on the property that bipartite graphs can be colored using only two colors.

4. Maximum Bipartite Matching Problem: Hungarian Algorithm

Now that we know how to determine whether a graph is a bipartite graph, we will focus on the maximum number of matches for a bipartite graph, that is, to find the largest possible set of edges in a bipartite graph such that no two edges share a common vertex. The algorithm is known as the Hungarian algorithm [10][11].

detailed steps

·Initialization: Begin with an initial feasible labeling of the graph. This labeling typically involves assigning zero potentials to all vertices in the first partite set (U) and initializing potentials for the vertices in the second partite set (V) such that they correspond to the maximum weight of edges incident to each vertex.

·Improving the Labeling: If no augmenting paths can be found, improve the labeling to make the graph more amenable to finding augmenting paths. This step often involves adjusting the potentials assigned to the vertices to create opportunities for augmenting paths to emerge.

·Repeat: Repeat steps 2 and 3 until no more augmenting paths can be found.

·Termination: Once no more augmenting paths can be found, the current matching is the maximum matching for the given bipartite graph.

The idea of the Hungarian algorithm is to take a bipartite graph that has been divided into two sets, go through the vertices in one set, and look for the vertices adjacent to it in the other set to match if the adjacent vertices have already been matched, then try to change this match, if not, then the matching attempt fails.

Take this bipartite graph as an example, we start from this vertex x, and match it to this vertex b, then this vertex y, we match it to a, then we go to this vertex z, and we find that the vertex adjacent to it in the right set is the vertex b, which has already been matched to x. So we tried to change this match, and fortunately, we found that x can be matched to d, in that case, the previous match between x and b is canceled, and we match z and b, x and d successfully. After the whole traversal, we can get the maximum number of matchings in the bipartite graph [12][13][14].

​C++ implementation code

bool find(int x) { //Hungarian Algorithm

for (int j = 1; j <= n; j++)

if (!st[j] && g[x][j]) {

//All unmarked points connected to x in the right set

st[j] = true; //Mark it to prevent multiple traversals

int t = match[j]; //match point for that point x in the right set

if (!t || find(t)) {

//If there is no object for t, it can match x. If there is, try to change the object, and if it can be changed, t matches x, and if it cannot change, then match failed

match[j] = x;

return true;

}

}

return false;

}

Recent studies have further optimized the Hungarian algorithm, explored new combinatorial approaches and improving computational efficiency [15][16]. These advancements contribute to faster and more efficient solutions for maximum bipartite matching, highlighting the ongoing evolution of algorithmic techniques in graph theory [17][18].

5. Conclusion

This paper comprehensively discusses the DFS algorithm and its application in determining whether a graph is bipartite using the graph coloring method. It also covers the Hungarian algorithm for finding the maximum matching in bipartite graphs. The C++ implementations provided demonstrate the practical application of these algorithms, highlighting their effectiveness in solving related problems. Current limitations and future improvements one of the limitations of this study is the lack of in-depth exploration of more advanced and recent algorithms related to bipartite graphs. Future research could focus on integrating machine learning techniques to enhance the efficiency of these algorithms. Additionally, expanding the experimental section to include real-world datasets and more complex scenarios would provide a more comprehensive understanding of their practical applications. Future studies should explore the development of new algorithms that can handle larger and more complex bipartite graphs efficiently. Integrating these algorithms with modern technologies such as big data analytics and artificial intelligence could unlock new possibilities and applications. Furthermore, investigating the use of bipartite graphs in emerging fields like bioinformatics and network security could provide valuable insights and advancements in these areas. By addressing these areas, future research can contribute significantly to the advancement of graph theory and its applications, paving the way for more innovative solutions to complex problems.