1. Introduction

With globalization progressing rapidly, international trade and transportation volumes continue to grow steadily, positioning shipping as a fundamental element in the global logistics system. Statistics reveal that shipping handles the majority of the world's trade, and ro-ro ships, due to their capability to load and unload vehicles and large goods quickly and efficiently, have emerged as crucial carriers in maritime transport. As transportation demands continue to rise, optimizing routes and enhancing transportation efficiency in the face of challenging maritime conditions have become critical issues that shipping companies must address urgently. Moreover, in today's context, where fuel costs are soaring and environmental regulations are becoming increasingly strict, route optimization is not just essential for improving economic performance but also plays an important role in advancing the sustainability of the maritime industry.

Currently, research on optimizing ship routes primarily revolves around two key types of methods: traditional optimization techniques and intelligent optimization algorithms. Traditional approaches, such as dynamic programming and linear programming, are quite effective when applied to smaller problems. However, as the scale of the problem expands, these methods often encounter difficulties related to a rapid increase in computational complexity, limiting their practical application in large-scale or highly complex scenarios. Additionally, traditional techniques tend to easily fall into local optimal solutions, meaning that they often fail to identify the best possible solution when confronted with multi-dimensional constraints. In recent years, intelligent optimization algorithms, including genetic algorithms and particle swarm optimization, have gained more attention and have been widely adopted in route optimization studies. These intelligent methods can overcome some of the challenges associated with traditional techniques to some degree. However, they also suffer from issues such as getting stuck in local optima and slow convergence, particularly when dealing with environments that undergo dynamic changes.

On the other hand, the Ant Colony Optimization (ACO) algorithm, which is inspired by biological behavior, has demonstrated clear advantages when tackling complex path optimization problems. This is mainly due to its strong global search ability and its efficiency in processing multiple tasks at once. The algorithm simulates the foraging behavior of ants, using pheromones to mark paths and guide ants toward the shortest route. This allows the algorithm to adjust paths dynamically to avoid getting stuck in local optima, gradually improving towards the best overall solution by using feedback mechanisms driven by pheromones. Consequently, the ant colony algorithm proves to be highly applicable and adaptable for complex, multi-constraint optimization challenges, such as optimizing routes.

Although the ant colony algorithm has been applied with success in areas like land-based logistics and transportation network optimization, its use in optimizing routes for ro-ro ships is still relatively limited. Most of the current research in this field has focused on container ships, with fewer studies aimed specifically at ro-ro ships, which have distinct operational characteristics. Moreover, many existing studies do not fully consider the combined influences of various factors like port berthing costs, ship loading efficiency, and weather conditions on the route selection process. Therefore, this study seeks to address these gaps by applying the ant colony algorithm to ro-ro ship route optimization, tackling key challenges that arise in this context, and providing shipping companies with scientific guidance on how to improve operational efficiency and lower fuel consumption.

In this research, an optimization model based on the ant colony algorithm will be developed to minimize the total costs of ro-ro shipping routes. The model will take into account factors such as the cost of berthing at ports, fuel consumption, and sailing time. Additionally, the study will analyze the effects of adjusting certain parameters, such as pheromone initialization, the rate at which pheromones evaporate, and the size of the ant colony, to ensure the results of the optimization are stable and efficient. By applying this model, the research aims to offer a practical solution for optimizing ro-ro ship routes, significantly reducing operating costs and providing essential technological support for shipping companies to compete effectively in the global market.

2. Method

2.1. Literature review

In the research background of route optimization based on ant colony algorithm to reduce the operating cost of ro-ro ship, it is particularly important to analyze the existing route optimization methods. As one of the core issues in the field of shipping management, route optimization aims to improve ship navigation efficiency and significantly reduce operating costs through scientific and reasonable planning. In recent years, with the rapid development of artificial intelligence technology, especially the unique advantages of ant colony algorithm in solving complex combination optimization problems, its application in the field of route optimization is increasingly widespread, which has brought revolutionary changes to the traditional shipping industry.

Ant colony algorithm, a bionic algorithm that simulates the foraging behavior of ants in nature, has achieved remarkable results in solving classical NP-hard problems such as traveling salesman problem (TSP) and vehicle routing problem (VRP) with its strong global search ability and adaptability. In the field of route optimization, ant colony algorithm can effectively explore the optimal or near-optimal route scheme connecting multiple ports or loading points by simulating the mechanism of pheromone deposition and volatilization during map search. For example, the work of Tsou MC and Cheng HC demonstrated the potential of ant colony algorithms to improve the efficiency of ship route planning, successfully reducing fuel consumption and operating time of ships by constructing efficient pheromone updating rules and heuristic strategies.[1]

In addition to the pure ant colony algorithm application, the hybrid algorithm strategy has gradually become a research hotspot. For example, the hybrid artificial bee colony algorithm proposed by Tong M et al. is optimized for the multi-warehouse multi-travel agent problem.[2] Although its direct application field is not route optimization, this study shows the possibility of improving the robustness and solving efficiency of the system by integrating the advantages of different algorithms. This method provides a new idea for route optimization research, that is, by combining ant colony algorithm with other meta-heuristic algorithms (such as genetic algorithm, particle swarm optimization, etc.), it may further break through the limitations of a single algorithm and achieve more precise and efficient route planning.

Specifically to the optimization of loading and route allocation scheduling of car ferries, Chen Pu's research uses integer programming method, although it does not directly use ant colony algorithm, but also reflects the effectiveness of mathematical programming method in solving specific types of route optimization problems.[3] Through accurate modeling, integer programming can find the optimal solution or feasible solution under given constraints, especially for small scale or clear structure problem scenarios. However, in the face of large-scale and dynamic route networks, relying solely on integer programming may face challenges of high computational complexity and insufficient flexibility.

Zhu Junjie's research considers the joint optimization of itinerant ship scheduling and speed under the influence of tides, which suggests that we must consider the influence of natural environment factors on navigation efficiency comprehensively when optimizing routes[4]. Such studies broaden the perspective of route optimization, emphasize the realistic adaptability and environmental sensitivity of the model, and provide important inspiration for the subsequent research on route optimization based on ant colony algorithm, that is, more variables and constraints in actual operation should be incorporated into the algorithm design.[5]

To sum up, the current route optimization methods are various, from traditional mathematical planning to modern heuristic algorithm, each has its own merits. Ant colony algorithm shows great potential in the field of route optimization with its unique advantages, but it also faces challenges such as how to further improve algorithm efficiency, enhance model adaptability and integrate various optimization techniques. Future research should be devoted to exploring more efficient, flexible and practical route optimization strategies, especially combining ant colony algorithm with other advanced technologies, so as to effectively reduce the operating costs of ro-ro ships and promote the sustainable development of the shipping industry while ensuring shipping safety and improving service quality.

2.2. Data

2.2.1. Port distance

Since the distance between ports has a direct impact on both sailing time and fuel consumption, it serves as a core parameter in the route optimization process. The distance data in this article comes from the Port Distance website, which provides detailed distance information between major ports in the world. The distance matrix will be used as a key input in the optimization algorithm[6].

2.2.2. Cargo volume

The cargo volume between ports is crucial to optimizing route selection and can help determine the priority of different ports. The cargo volume data used in this article comes from Clarksons Research, a database covering the flow of car carriers between ports and forecast information. These data will be used to evaluate the transportation demand and revenue of each route.

2.2.3. Ship operating costs

The operating cost of a ship is a key factor in route optimization, involving fuel consumption, crew wages, maintenance costs, etc. The operating cost data used in this article comes from the shipping-related cost calculation formula and the data of shipping supporting service providers. These data can accurately reflect the actual operating expenses of ro-ro ships and provide reliable cost input for the model, so as to minimize the total cost when optimizing routes.

2.2.4. Port charges

Port charges include parking fees, loading and unloading fees, pilotage fees and other costs, which vary from port to port. This article obtains port charge data through the official websites of multiple ports and the port charge standards issued by the government. These data are used to calculate the comprehensive berthing costs of different ports, which in turn affects the route selection and the estimation of total operating costs.

2.3. Analysis of the current situation of the newly opened route of ship

2.3.1. Route and port of call

The RO-ro shipping Routes selected in this study are based on the statistical data of "Major Seaborne Car Trade Routes" in the Clarkson Car Carrier Trade & Transport 2023 report. The report provides detailed analysis and statistics on the major automobile maritime trade routes worldwide, providing information on the core routes of automobile RORo transportation between various countries and regions. In this study, routes from Asia-Pacific, Middle East and Europe are selected as the basic data source for RO-RO shipping routes. After identifying countries and regions with large automotive exports and imports (such as Japan, South Korea, EU/UK, China, and Turkey), etc. In order to further refine the construction of the route model, this study selects the port with the highest vehicle throughput in the past 12 months as the representative port from the major ports of various countries provided in the Clarkson report to ensure the timeliness of the data and simplify the route planning process. To further clarify the model, the portion not listed in the main route is treated as 0 cargo volume.

After the port is determined, this paper uses the data of ship communication network and port distance to calculate the sailing distance between ports. Specifically, through the statistics of the average sailing distance between different ports, this study obtained accurate shipping distance data, which provided basic support for the calculation of sailing cost, fuel consumption and ship configuration. The final route network and port list are shown in Table 1, which details the ports of departure and destination of each route, the countries or regions in which they are located, and the specific sailing distance between the two ports.

Table 1. Information about each route

2.3.2. Route cost calculation

This paper refers to the cost structure in the literature, and mainly considers the unit voyage cost and berthing cost of three ship types. Due to the differences in shipping capacity, fuel consumption and maintenance costs, the unit voyage cost and port berth cost of different sizes of ships are significantly different. Therefore, in the cost calculation, the sailing and docking costs of each ship type are analyzed in detail.

1. Unit voyage cost

Unit sailing charges include fixed charges and fuel charges. Fixed expenses mainly refer to the unavoidable expenses in the daily operation of the ship, such as crew salaries, maintenance costs, etc. Fuel costs are calculated based on the fuel consumption rate and range of each ship type. According to the literature, the unit sailing cost per nautical mile is obtained by synthesizing all the costs.

2. Parking charges

Berthing charge refers to the port charge payable when a ship berthing in a port. Due to the different scale, facilities and service level of each port, the parking fees are also different. The charging standard of this paper is based on the charging standard of Chinese ports for different deadweight ton RO-ro ships. Detailed cost data are shown in Table 2.[7]

Table 2. Information and charges for different ship types

2.4. Optimization and analysis

2.4.1. Model assumption

In order to simplify the model and ensure the feasibility of calculation, this paper makes the following assumptions when constructing the RO-ro ship route optimization model:[6]

1. Demand certainty

It is assumed that the demand for automobile transportation between ports is certain and does not fluctuate with time, that is, the demand remains unchanged throughout the transportation process.

2. Fixed ship types and costs

Three ship types (4000RT, 5000RT, 6000RT) are considered in the model, and their unit sailing costs and berthing costs are known and fixed, and do not fluctuate with market prices or other factors.

3. Port loop route

The model assumes that the RO-ro ship travels in accordance with the loop route, that is, all ships start from the starting port, visit each designated port in turn and return to the starting port, forming a closed-loop structure.

4. No adverse weather

Assuming that there is no weather or other external factors affecting the entire transportation process, that is, the ship travels at a fixed speed between ports and there is no additional delay or disruption.

5. Port operation time is ignored

In the model, the loading and unloading time at each port is ignored, that is, it is assumed that the berthing time of the ship at each port is the same and has been included in the berthing cost, which will not affect ship scheduling.

2.4.2. Model establishing

1.Model symbol definition

To facilitate the expression of model structure and formula derivation, the following symbols are defined in this paper:

i,j: Port index number, i,j=1,2,... N, where n represents the total number of ports.

k: index number of ship type, k=1,2,3, corresponding to three different ship types (4000RT, 5000RT, 6000RT).

Dij: Sailing distance from Port i to Port j (in nautical miles).

Qij: Transport demand from Port i to Port j (units: vehicles).

Ck: The unit voyage cost (in USD/nautical mile) of ship type k, i.e. the cost per nautical mile traveled by ship type k.

Pk: The berthing fee of ship type k at the port (unit: USD/time), that is, the cost of each berthing at the port.

Lk: The single load capacity (unit: vehicles) of ship type k, that is, the number of vehicles that can be carried per ship of that ship type.

xijk: binary decision variable, if ship type k performs a voyage from port i to port j, then xijk=1, otherwise xijk=0.

Nijk: The number of ships required for ship type k to travel from Port i to Port j.

TC: Total transportation cost, is the optimization object of the objective function, representing the sum of the costs of the entire transportation network.

2.Objective function

The objective of this model is to optimize the route and ship configuration of RO-RO ships by ant colony algorithm to minimize the total transportation cost. To this end, the model establishes an objective function and introduces a series of constraints to ensure that the transportation demand between ports is satisfied and the route selection is optimal.

TC represents the total cost of the entire transport network and covers the sailing cost and berthing charges for each leg of the voyage. The formula for minimizing the total cost is defined as:

\( TC=\sum _{i=1}^{n}\sum _{j=1}^{n}\sum _{k=1}^{3}({D_{ij}}∙{C_{k}}∙{x_{ijk}}+{P_{k}}∙{N_{ijk}}∙{x_{ijk}})\ \ \ (1) \)

Among them:

Dij⋅Ck⋅xijk represents the sailing cost of ship type k from Port i to Port j. The Ck varies by ship type and is multiplied by the distance Dij to obtain the total voyage cost for each leg.

Pk⋅Nijk⋅xijk represents the total cost of berth in port for ship type kk. The berthing cost Pk is set according to the ship type, multiplied by the number of ships required for the voyage Nijk, to get the berthing cost of the section.

3. Constraint condition

In order to ensure the rationality and operational feasibility of the model, the following constraints are set:

(1)Demand satisfaction constraint

The ship configuration for each leg of the voyage needs to meet the demand between ports. To ensure that all cargo transportation tasks between ports are completed. Specifically, the capacity of all configured ship types should be greater than or equal to the demand:

\( \sum _{k=1}^{3}{L_{k}}∙{N_{ijk}}∙{x_{ijk}}≥{Q_{ij}} , ∀i,j \ \ \ (2) \)

Among them, Lk is Ship form k's single load capacity.

(2)Vessel selection constraints

Select the smallest vessel type that meets demand for each leg of the voyage to minimize costs. The ship type is selected based on the capacity to meet the demand and to ensure that the number of ships is as small as possible.

(3)Path uniqueness constraint

The navigation path from port i to port j must be unique, that is, each path can only be executed by one ship type. If one ship type chooses to perform a voyage from Port i to Port j, no other ship type can choose that route at the same time:

\( \sum _{k=1}^{3}{x_{ijk}}≤1 , ∀i,j \ \ \ (3) \)

(4)Number of ships constraint

The number of ships required for each leg of the voyage Nijk shall be calculated based on the demand and the loading capacity of the ship type to ensure that all demands are met and to avoid too many or too few ships.

\( {N_{ijk}}=⌈\frac{{Q_{ij}}}{{L_{k}}}⌉, ∀i,j,k \ \ \ (4) \)

(5) Closed-loop constraint

In order to ensure the closed-loop characteristics of the route, the route of all ships is required to form a complete loop, that is, to start from the port of origin and return to the port of origin after visiting other ports.

\( {x_{i(i+1)k}}={x_{(i+1)ik}} , ∀i=1,2,…,n,∀k\ \ \ (5) \)

(6) Non-negative constraint

All decision variables are non-negative integers, that is, the routing variable xijk and the number of ships Nijk must be non-negative integers.

\( {x_{ijk}}ϵ\lbrace 0,1\rbrace , {N_{ijk}}≥0 \ \ \ (6) \)

2.4.3. Model solving

The core goal of solving is to find the optimal ring route through ant colony algorithm, minimize the total transportation cost, and meet the transportation needs between ports. In the algorithm, it is assumed that there are several "ants" departing from the starting port, and each ant represents a possible route plan. [6]Each ant chooses a path based on its pheromone concentration and the path's attractiveness. In each iteration, the pheromone is updated based on the quality of the path, gradually guiding the ants toward the lowest-cost path choice. Finally, through multiple iterations and pheromone accumulation, the algorithm converges to the loop route with optimal cost.

1.Ship route strategy

In order to ensure the practicability of the model, the ship route strategy must meet the following conditions:

Meeting transportation needs: On each voyage, the appropriate ship type and number of ships must be configured to ensure that the transportation needs between ports are met.

Minimum cost configuration: Select the most economical ship type and the smallest number of ships for each leg of the voyage to minimize the total cost of transportation.

Loop loop: The route must form a closed loop, that is, start from the start port, visit all the target ports and return to the start port to ensure that the route is closed.

Specifically, the algorithm selects the smallest ship type to meet the requirements for each leg of the route and calculates the sailing and berthing costs for each leg. The ultimate goal is to choose a loop route with the lowest total cost.

2.Path construction of ant colony algorithm

During path construction, each ant builds a complete circular path from the starting port. The specific steps of path construction are as follows:

(1)Route selection

Each ant starts from the current port and selects the next port based on the pheromone concentration of other ports and the attraction of the path (the attraction of the path is determined by the reciprocal of distance and transportation cost). The selected probability calculation formula is as follows:

\( {P_{ij}}=\frac{{[{τ_{ij}}]^{α}}∙{[{η_{ij}}]^{β}}}{\sum _{k}{[{τ_{ij}}]^{α}}∙{[{η_{ij}}]^{β}}} \ \ \ (7) \)

Where:

τij is the pheromone concentration from port i to port j;

ηij =1 /distanceij/costij is the reciprocal of the path attraction;

• α and β are weight factors for pheromone and attraction, respectively.

(2)Path construction

Each ant selects the port in turn until a complete path is formed. For each section of the path, the type and number of vessels required are calculated, and navigation and berthing costs are accumulated. In this example, the ants select the smallest boat type that meets the demand and determine the number of ships needed by calculating the load capacity.

(3)Path loop

When the ant reaches the last port, it returns to the starting port, forming a complete circular path. This process ensures that all path structures meet the requirements of circular routes.

3. Pheromone renewal

After the path construction is complete, pheromone updates are performed at the end of each iteration. The steps of pheromone updating include two parts: pheromone volatilization and pheromone accumulation to help the algorithm converge to the optimal solution in multiple iterations.

(1)Pheromone volatilization

Pheromone will be volatilized in a certain proportion after each iteration to avoid the algorithm falling into local optimal. The formula of pheromone volatilization is:

\( {τ_{ij}}=(1-ρ)∙{τ_{ij}} \ \ \ (8) \)

Among them,ρis the volatilization rate of pheromone.

(2) Pheromone accumulation

For a lower-cost path in the current round, additional pheromones are added to make that path more attractive in subsequent iterations. The formula for pheromone increment is:

\( ∆{τ_{ij}}=\frac{Q}{{cost_{ij}}} \ \ \ (9) \)

Where Q is the pheromone increment factor and costij represents the cost of the path. Through the pheromone accumulation mechanism, the low-cost path will have a higher selection probability in subsequent iterations, thereby helping the algorithm gradually find the optimal path.

4.Process of algorithm solving

(1)Initialization

Set the number of ants, pheromone concentration, parameters and other initial values, initialize the pheromone matrix and the optimal path variable.

(2)Path construction

Each ant starts from the starting port, and gradually chooses the next port according to the pheromone concentration and path attraction to build a complete path. For each section of the route, the minimum ship type and number of ships that meet the requirements are selected and the path cost is calculated.

(3)Cost calculation

For each path constructed by an ant, the total cost of the path is obtained by summing up the sailing costs and berthing costs of all segments. The total cost is compared to the current best cost, and if it is better than the current best cost, the best path and the best cost are updated.

(4)Pheromone update

At the end of each iteration, the pheromone volatilization and accumulation operations are carried out on all paths to update the pheromone matrix. Pheromone increment depends on the path cost, and the low-cost path will obtain more pheromones, increasing its selection probability in subsequent iterations.

(5)Iteration

Repeat steps 2 through 4 until the maximum number of iterations is reached or convergence conditions are met.

(6)Output result

After the algorithm is finished, output the circular path with the lowest total transportation cost, as well as the ship type selection, the number of ships required and the corresponding cost for each voyage on the path[8].

3. Results

In this study, the RO-RO shipping route was optimized and a closed-loop loop route covering Shanghai - Pyeongtaek - Nagoya - Derince Burnu - Jebel Ali – Antwerp Bruges – Dammam - Shanghai was designed to meet the transportation needs between all ports and achieve the lowest transportation costs. The route passes through China, South Korea, Japan, Turkey, UAE, EU/UK, Saudi Arabia and other major ports in turn, and finally returns to China, forming a complete closed cycle. In the specific design, this paper takes this route as an optimization example to achieve the optimal cost control effect, and provides reference for other route design.

In this design, each leg of the voyage is selected according to the demand for the optimal type of ship to meet the traffic volume and the required minimum number of ships, to ensure that the demand between ports is met, while the total cost is kept to a minimum. The route is designed to take into account the operating costs and berthing costs of the ship during each leg of the voyage. Operating costs are determined by the distance a ship travels and unit voyage costs, while berthing costs include loading and unloading, inspection and other additional costs incurred while the ship is in port. The design concept is based on the principle of "demand matching and optimal distribution", that is, the smallest ship type meeting the demand is selected on each section of the route to ensure the maximization of transportation benefits.

In the optimization process, each "ant" starts from the starting port through the guidance of pheromones, and selects the next port in turn to form a complete navigation path. Specifically, the model avoids inefficient port routing by selecting routes with higher route attraction (determined by demand, distance, and navigation costs). The algorithm updates the pheromone after each iteration, making the low-cost path more attractive in subsequent iterations, thereby gradually converging to the optimal solution.

The basic concept of the optimal loop route design is "the lowest cost, meet the demand" as the core, taking into account the port needs, ship carrying capacity and navigation costs. Through continuous iteration and dynamic adjustment of pheromones, the model finally gets a cost minimization loop route, and achieves the exact match between cost and transportation demand on each route. This route design not only effectively reduces unnecessary transportation costs, but also optimizes the utilization rate of ships through reasonable allocation of ship type and number.

Figure 1 shows the route layout of a circular route. The optimized route geographic map shows the route layout, which is helpful for decision makers to intuitively understand the rationality of the route. The model optimization results show that ant colony algorithm has obvious practicability and applicability in complex ro-ro ship transportation network optimization.

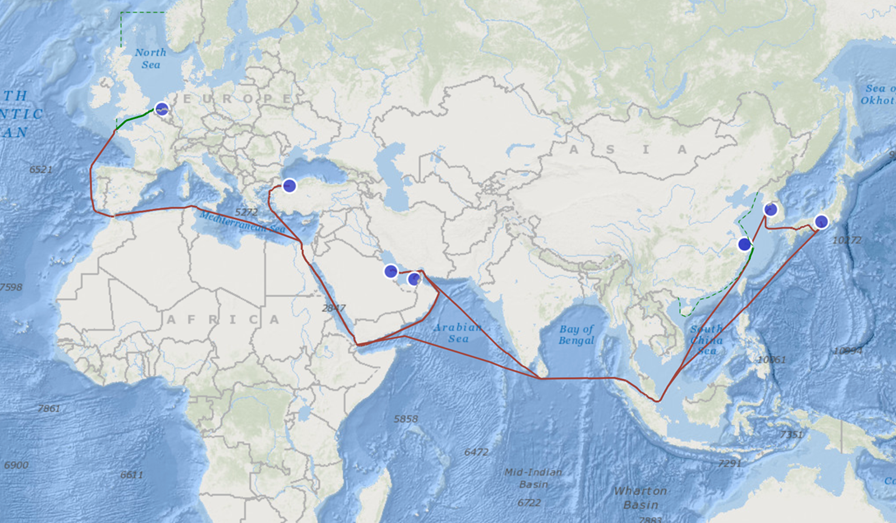
Figure 1. Ro-ro shipping route

4. Conclusion

In this study, ant colony algorithm is used to optimize the ring route in the RO-ro shipping network, and good cost control effect is achieved. However, although the model successfully reduces the total transportation cost and improves the transportation efficiency, there are still some problems worthy of further discussion in its practical application, and there can be more room for further research in the future.

First, the model assumes that transport demand and costs between ports remain constant throughout the transport cycle. However, in fact, transportation demand is often affected by market fluctuations, seasonal changes and other factors, showing dynamic changes. Such fluctuations in demand can lead to overcrowding or underloading on existing routes at certain times, affecting operational performance. In order to solve this uncertainty, future research can introduce a demand prediction model, and on this basis, combined with a dynamic adjustment mechanism, so that the route can be flexibly adjusted with the change of demand, so as to improve the applicability of the model and the elasticity of the route.

Secondly, this model only considers the direct transport between ports, and does not involve the design of trans-shipment and layered network. In actual high-demand areas, shipping companies often use a combination of hub and feeder ports to build a multi-tiered transport network. This layered mode can effectively divide the cargo and improve the transportation efficiency, which helps to allocate the transportation capacity more rationally. In the future, transport conditions can be incorporated into the model to establish a "center-branch" multi-level network structure. In this model, the main routes can concentrate on handling large-scale shipments, while the feeder ports are responsible for the distribution of small, dispersed cargo flows. This not only relieves the strain on the capacity of a single route, but also further reduces the total transport cost through rational allocation of capacity.

In addition, although ant colony algorithm has strong global search ability and dynamic adaptability in route selection, it may still fall into local optimal solutions in complex transportation networks, resulting in unsatisfactory solutions. In order to improve the stability and solving effect of the model, future research can try to combine ant colony algorithm with other optimization algorithms (such as genetic algorithm and particle swarm optimization algorithm) to build a hybrid optimization model. Through the complementary advantages of various algorithms, the hybrid model can effectively find a more balanced result between the initial solution and the local optimal solution, so as to improve the computational efficiency and solution accuracy of large-scale route optimization.

Finally, the model does not consider the tradeoff between fuel costs and carbon emissions. Under the trend of global carbon emission reduction policies, shipping companies should not only pay attention to economic benefits, but also need to control carbon emissions. Therefore, the introduction of environmental factors into the route optimization model and the comprehensive consideration of fuel efficiency and carbon emissions will be more in line with the current needs of green shipping development. By increasing the cost of carbon emissions or setting limits on carbon emissions, the model can strike a balance between economic benefits and environmental requirements, providing a more reasonable solution for the future development of sustainable shipping.

In summary, the ant colony algorithm is used in this study to optimize the ring route design of the RO-ro ship successfully and achieve good results in cost control. If the factors such as demand dynamic prediction, transport conditions, multi-algorithm integration and environmental constraints can be combined, future research will help to further enhance the practical application value of the model and provide more comprehensive guidance for the optimization of the RO-ro ship transport network.