1. Introduction
Currently, Proportional-Integral-Derivative (PID) controllers offer advantages such as fast response times and low dynamic error, making them widely used in the measurement of pressure and temperature in industrial production [1]. However, conventional PID controllers face challenges in maintaining system stability, as they are prone to various interference factors that can result in system instability, overshoot [2], and difficulty in achieving precise control. Traditional PID algorithms have immutable parameters, whereas neural network models demand extensive raw data for their training, neural network-based improvements to PID controllers often lack universality, presenting significant technical limitations.
Speaking about the stability of nonlinear systems, both domestic and foreign research has generally been involved in designing new approaches to enhance response time and precision of PID controllers. However, due to the inherent nonlinear characteristics of these systems, certain challenges remain, including but not limited to: 1. Although integrating neural network methodologies into the PID control algorithm has significantly improved control precision and expanded its applicability across various models, the initial parameters of the controller are highly sensitive to experimental data [3], which reduces the robustness of the algorithm. As a result, this sensitivity complicates the tuning process, making it more difficult to achieve optimal system performance; 2. Training neural network models requires substantial computational resources and large amounts of raw data, which can pose challenges in control systems with limited computational capacity.
Given the wide variety of neural networks, this paper provides a comprehensive review of PID controllers enhanced through neural networks, both domestically and internationally. First, it summarizes the most widely applied neural network algorithms, highlighting their advantages and disadvantages. Next, it examines the shortcomings of mainstream algorithms and compiles a summary of these limitations. On this basis, the paper introduces specific optimization methods for improving these algorithms, providing valuable references for future research on the integration of neural networks and control systems.
2. Introduction to the Principle of the PID Algorithm
PID is a control algorithm based on proportional, integral, and derivative operations. Due to its simple structure, robust stability, fast adjustment speed, and well-developed theoretical foundation, PID has been widely applied in the stability control of various systems, such as those regulating temperature, pressure, and flow. The proportional operation, as the basic control component of the algorithm, is the core part of the PID algorithm. It reflects the system's error in proportion to the magnitude of the deviation but is unable to eliminate steady-state errors. The integral operation eliminates the system's steady-state failures. The integral action's power is time-dependent; unless the steady-state mistake is removed, the integral effect gets weaker as the time constant increases.
The derivative operation, on the other hand, accelerates the system's response time. It accurately reflects the rate of change of the system error and promptly introduces corrective actions before the system error signal escalates significantly, thereby significantly reducing the system's overall reaction time. The formula for the PID controller is expressed as follows:
\( u(k)={K_{p}}e(k)+{K_{i}}\sum _{n=0}^{k}e(n)+{K_{d}}(e(k)-e(k-1)) \) | (1) |
In the PID control formula, u(k) represents the output curve, \( {K_{p}} \) is the proportional gain or scale coefficient, \( e(k) \) represents the error curve, The integral time constant is \( {K_{i}} \) , and \( { K_{d}} \) is the derivative time constant.
In control systems, most systems are inherently nonlinear. The state of the system and its output variables, influenced by external conditions, cannot be accurately described by a linear relationship. Traditional linearized models struggle to maintain the stability of various system parameters when large disturbances occur. As a result, these models often fail to provide adequate control performance in nonlinear environments.
3. Improved nonlinear stability control based on neural network
3.1. PID algorithm enhanced by RBFNN algorithm
In the literature, Radical Basis Function Neural Networks (RBFNN) [4] have been employed to further improve the PID controller algorithm based on the nonlinear U model [5]. This enhancement significantly
|
| |
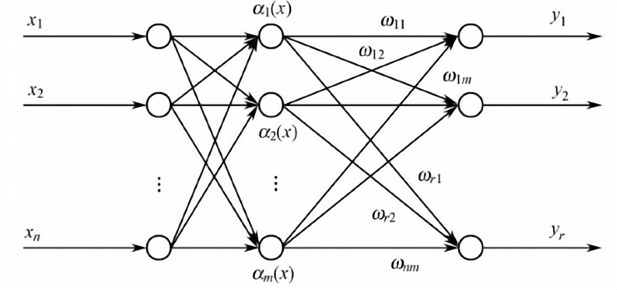
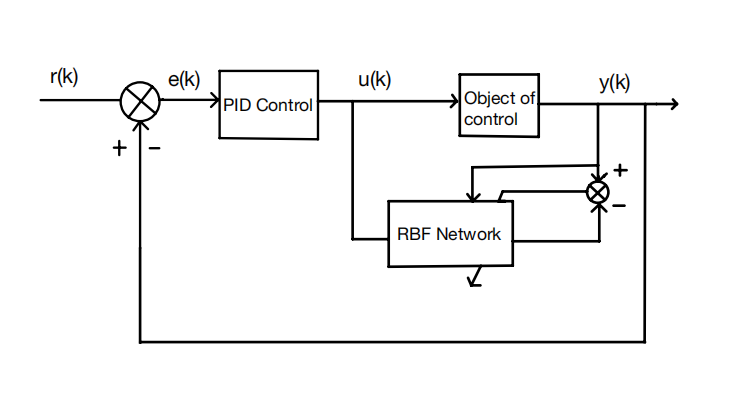
Figure 1: Structure diagram of RBFNN. | Figure 2: RBF neural network tuning PID parameter control structure. |
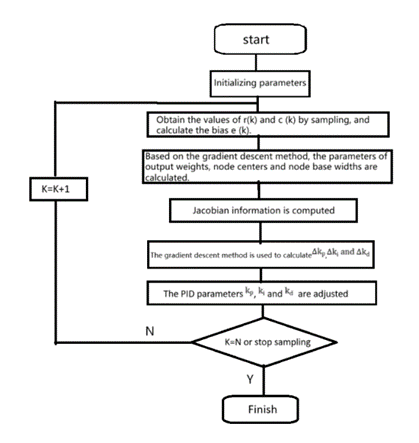
Figure 3: Flow chart of PID control optimization by RBF neural network.
improves the anti-interference capability and control accuracy of the controller, extending its applicability far beyond that of traditional PID controllers.
The basic principle of the U model mentioned in the literature is to establish a time-varying relationship between the system's output and control signal, utilizing output feedback signals to represent a class of nonlinear systems. The U model is highly applicable to nonlinear systems due to its flexibility and adaptability. This is how it is expressed:
\( y(t)=\sum _{j=0}^{M}{a_{j}}(t){u^{j}}(t-1)+{e_{j}}(t) \) | (2) |
In the U model expression, M represents the order of the nonlinear system, y(t) represents the output of the nonlinear system, and \( {a_{j}}(t) \) represents the timing coefficient in the nonlinear system expression.
Radial Basis Function Neural Networks (RBFNN) are a specialized type of feed-forward neural network that possess the capability to effectively overcome local minima problems and attain rapid convergence. Figure 3 depicts the structure of an RBFNN, which has three layers. Input layer: Composed of several sensing units, this layer represents the source node input; Hidden layer: Contains
radial basis neurons that perform nonlinear mapping, transforming low-dimensional, non-linearly
|
| |
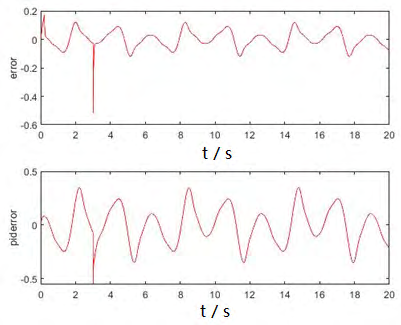
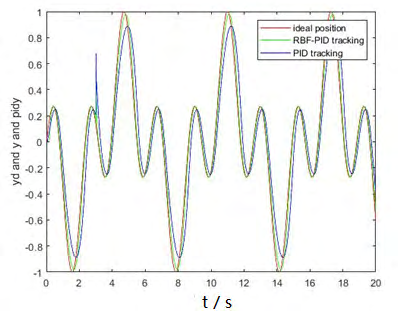
Figure 4: Error comparison of the two algorithms [6]. | Figure 5: Output comparison of the two algorithms. |
separable inputs into a high-dimensional separable space; Output layer: Composed of linear neurons, this layer performs linear weighting on the information provided by the hidden layer neurons, outputting the result of the entire neural network.
RBF neural networks often employ the Gaussian function as their basis function, which is represented as follows:
\( {y_{j}}(x)=exp(-\frac{{‖x-{c_{j}}‖^{2}}}{2σ_{j}^{2}}) j=1,2......,m \) | (3) |
Where \( {c_{j}} \) represents the output of the j-th hidden layer node, X= \( {({X_{1}},{X_{2}},……, {X_{i}},……,{X_{n}} )_{T}} \) , i=1,2,…,n, is the input sample vector; \( {C_{J}} \) =( \( {C_{j1}} \) , \( {C_{j2}} \) ,…… \( {C_{Jji}} \) ,……, \( {C_{jjn}} \) ) represents the center vector of the Gaussian function at the j-th node of the hidden layer; \( σ_{j}^{2} \) is the normalization parameter of the j-th node, which determines the scope of the central basis function. The output range of the hidden node is between 0 and 1, and the distance between the center and the input sample is inversely proportional to the response of the hidden node.
In the literature, a new nonlinear PID control structure is proposed by combining the U model and the Radial Basis Function Neural Network (RBFNN). The structure in figure 4 consists of two main parts: the PID controller and the RBF network. The PID controller is responsible for the direct closed-loop control of the controlled object, while the RBF network adjusts the PID controller based on system input information, achieving more stable control. This adjustment demonstrates the self-learning capability [7] of the neural network. The flowchart of PID control optimization is shown below. Finally, the designed control algorithm, along with the traditional PID control algorithm, was rigorously tested using a nonlinear triangular complex function as the input signal, and the comparative results of this analysis are presented in the accompanying figures.
As seen from figure 6 and 7, the error fluctuation of the RBF-improved control algorithm is smaller, and the output is more consistent with the input signal. Therefore, the literature conclusively demonstrates that the RBF-PID controller network exhibits superior performance compared to the traditional PID controller.
The literature also highlights that the traditional PID controller, optimized using RBF and the U model as the nonlinear model, significantly improves system stability and control accuracy compared to the traditional PID controller. These improvements address many of the shortcomings of traditional nonlinear PID controllers. However, during MATLAB simulations, multiple adjustments to the neural network's parameters, learning rate, and momentum factors were required. This indicates that the initial system parameters still have a considerable impact on the control model, limiting its applicability across different systems. Future study could concentrate on enhancing the control algorithm's resilience and minimizing its susceptibility to starting settings.
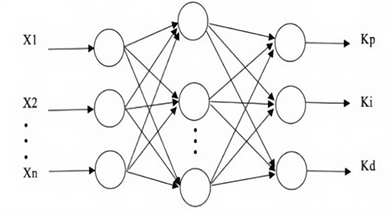
Figure 6: Structure diagram of BP neural network.
|
| |
Figure 7: A BP neural network-integrated PID control system. | Figure 8: Step response curves of the two systems. |
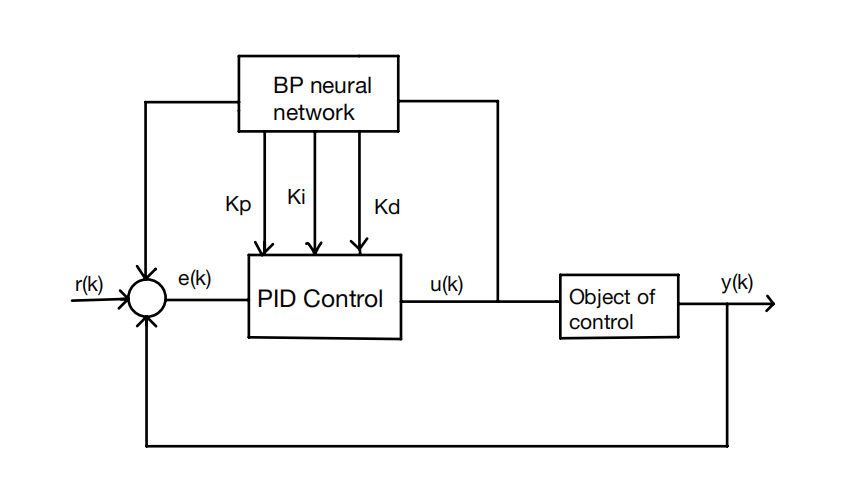
3.2. Improved PID algorithm based on BP neural network
In industrial furnace temperature control, the controlled object often exhibits characteristics such as non-linearity and time variability. In this paper, a PID control method utilizing a Back Propagation neural network is proposed to enhance the accuracy and stability of the temperature control system.
BP neural networks are multi-layer feed-forward neural networks that are trained utilizing an error back propagation technique. [9]. They possess powerful nonlinear mapping capabilities and can adjust weights through the back propagation of errors, allowing the network output to gradually approach the desired value. By utilizing a BP neural network, the parameters of the PID controller can be dynamically adjusted in accordance with real-time conditions, thereby optimizing the overall dynamic performance of the system.
Similar to the RBF neural network mentioned earlier, the BP neural network has three layers: input hidden and output layers. In this study, the parameters of the neural network were first adjusted based on the structure and characteristics of the furnace temperature control system, and the network was trained to develop the controller model. Subsequently, a specific controller was designed using the PID control parameters obtained from the training process.
The working principle of the system operates as follows: by effectively leveraging the nonlinear function approximation and robust learning capabilities of the BP neural network, the output neurons within the BP network are specifically designed to correspond to the three critical parameters, namely KP, Ki, and Kd , in the PID controller. These parameters are adjusted dynamically to optimize the target performance indicators. In this system, r(k) represents the set input, y(k) is the actual output of the controlled object, u(k) represents the output generated by the PID controller.
To assess the efficacy of the developed controller, MATLAB simulations were conducted. The settings for the BP neural network are as follows:
• Number of layers: 3
• Number of hidden layer: 8
• Number of input layer : 3
• Number of output layer : 3
• Activation function: Sigmoid
• Weight initialization algorithm: Gaussian distribution
• Network weight update frequency: each iteration
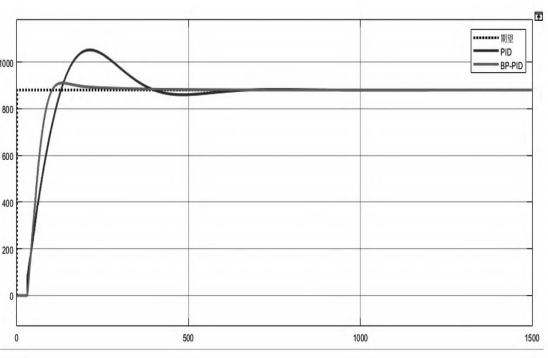
The BP-PID controller and a traditional PID controller were introduced into the system, and a nonlinear, time-delay induction heating system was used as the controlled object in the simulation experiments. According to the curve displayed in the accompanying figure, it is evident that the BP-PID controller boasts a faster response speed compared to the conventional PID controller. Additionally, when the system attains a steady state, the overshoot generated by the BP-PID controller is markedly smaller. It can be concluded that the PID control system designed in this paper, based on the BP neural network, demonstrates excellent robustness and dynamic stability. Even in systems subject to significant environmental disturbances, the BP-PID controller shows superior performance and can achieve more accurate control of furnace temperature.
4. Discussion
In recent years, the evolution of neural networks has notably broadened the horizons for research across various domains. Combining nonlinear PID controllers, known for their robustness and computational accuracy, with neural networks that possess strong learning capabilities has become a prominent research direction. However, current nonlinear control algorithms, improved by neural networks, still exhibit limitations and require adjustments for different control systems. This paper primarily introduces several recent cases where the combination of nonlinear PID and neural network algorithms has been applied for system improvements. The advantages and disadvantages of these approaches, compared to previous improvements, are summarized and analyzed as follows:
A RBF neural network [1] was used to enhance the performance of the controller, allowing for real-time adjustments based on the system's input information. This yielded a controller that could have improvement in learning and adaptation capabilities. From the output comparison chart, it is clear that the PID controller enhanced with the RBF neural network shows smaller error fluctuations and better alignment to the given input signals. In the process of debugging, however, great changes had to be effected in the neural network parameters, the learning rate, and the disturbance factors. This makes it clear that these initial parameters have much to do with system performance. If the starting values are not correctly set, it may affect the system's true applicability in practice. This could probably be another study in designing neural networks that are not sensitive to initial parameters, which would go a step further in enhancing system performance.
A BP neural network was integrated with PID control [2], utilizing the learning capabilities of the BP neural network to autonomously tune PID parameters. This approach addressed the limitations of traditional PID controllers when handling the nonlinear, time-varying characteristics of industrial furnace temperature control. However, one notable shortcoming of the BP neural network is that it necessitates a considerable and comprehensive amount of historical data for effective training. In certain scenarios, acquiring sufficient data may be challenging, making it difficult to establish an effective controller model. Additionally, in complex nonlinear system environments, while the BP neural network can adjust parameters automatically [10], its accuracy and response speed may not always be adequate, potentially impacting overall control effectiveness.
Improved PID controllers based on neural networks can give full play to the learning ability of neural networks and have obvious advantages in overcoming the deficiencies of traditional PID control systems facing nonlinear complex environments. The simulation tests for improved PID controllers and traditional PID controllers were performed for several real-world application scenarios; it was proved that enhanced PID controllers have better dynamic performance and robustness. But there is one important obstacle: most of the neural networks are very sensitive to the starting parameters. Further research could be directed at creating neural networks that are less sensitive to initial conditions, for further achievement in controller performance. Moreover, integrating genetic algorithms (GA) [11] and particle swarm optimization (PSO) [12] with neural networks may enhance the initialization and tuning of PID parameters. Another promising approach involves using dual neural networks [13] —one to identify system parameters and the other to optimize PID parameters based on the identified results—potentially mitigating the sensitivity to initial parameters.
In conclusion, PID controllers improved by neural networks have demonstrated significant advantages in managing nonlinear, time-varying, and complex systems. Future research could focus on further optimizing the structure and algorithms of neural networks to address the adaptability issues of the controller and enhance their overall performance.
5. Conclusion
This paper first introduces the principle of PID algorithm and the advantages of PID controller in actual industrial production. Then it analyzes the two PID control algorithms based on neural network improvement that are currently used more: the PID control algorithm based on RBF neural network improvement and the PID algorithm based on PB improvement. It introduces the control algorithm principle and the structure of neural network. And it discusses the advantages and current defects of the two algorithms in actual application environment respectively. The RBF neural network can adjust the controller in real time according to environmental factors to make the error smaller, but it is greatly affected by the initial parameters. The BP neural network can handle nonlinear environments well, but it needs a large amount of historical data to train it to achieve stable control effects. Finally, the paper summarizes the current PID control algorithms based on neural network improvement and looks forward to the areas that need to be improved: improving the controller using neural networks with low sensitivity to parameters using genetic algorithms or designing dual neural network controllers.
References
[1]. A Haiyang, Z., Yu, S., Deyuan, L., & Hao, L. (2016). Adaptive neural network PID controller design for temperature control in vacuum thermal tests. 2016 Chinese Control and Decision Conference (pp. 458-463).
[2]. Nguyen, N., & Nguyen, P. (2018). Overshoot and settling time assignment with PID for first‐order and second‐order systems. IET Control Theory & Applications, 2023.
[3]. Li, J., Peng, T., Zhang, S., & Liu, C. (2023). Improved PID Controller Based on BP Neural Network. Journal of Physics: Conference Series, 2479.
[4]. Attaran, S., Yusof, R., & Selamat, H. (2016). A novel optimization algorithm based on epsilon constraint-RBF neural network for tuning PID controller in decoupled HVAC system. Applied Thermal Engineering, 99, 613-624.
[5]. Mao, Q., & Ge, S. (2020). A Parallel Nonlinear Control System of Improved Generalized Predictive Control and Single Neuron PID Based on U-model. 2020 7th International Conference on Information Science and Control Engineering (pp. 1595-1599).
[6]. Nie, L., Jiayi, G., Lu, C., Zheng, H., & Zhishuai, Y. (2018). Longitudinal speed control of autonomous vehicle based on a self-adaptive PID of radial basis function neural network. Iet Intelligent Transport Systems, 12, 485-494.
[7]. Lei, Y., Ma, J., Liu, M., & Liu, P. (2021). Research on Intelligent PID Control Algorithm Based on Neural Network. 2021 International Conference on Intelligent Transportation, Big Data & Smart City (pp. 325-328).
[8]. Li, J., Peng, T., Zhang, S., & Liu, C. (2023). Improved PID Controller Based on BP Neural Network. Journal of Physics: Conference Series, 2479.
[9]. Hameed, A., Karlik, B., & Salman, M. (2016). Back-propagation algorithm with variable adaptive momentum. Knowl. Based Syst., 114, 79-87.
[10]. Lu, H.; Ma, X. & Ye, Y. (2023). Energy coupling control of bridge crane based on adaptive fuzzy strategy. Journal of Physics: Conference Series, 2479, 012055.
[11]. Rodríguez-Abreo, O., Rodríguez-Reséndiz, J., Fuentes-Silva, C., Hernández-Alvarado, R., & Falcón, M. (2021). Self-Tuning Neural Network PID With Dynamic Response Control. IEEE Access, 9, 65206-65215.
[12]. Yang, X., Chen, X., Xia, R., & Qian, Z. (2018). Wireless Sensor Network Congestion Control Based on Standard Particle Swarm Optimization and Single Neuron PID. Sensors (Basel, Switzerland), 18.
[13]. Na, L. (2013). Improved Neural Network PID Controller of Joint Robots. Control Engineering of China, 20.
Cite this article
Fu,X. (2025). Neural Network-Enhanced Nonlinear PID Control: Advances in Stability, Robustness, and Real-World Application. Applied and Computational Engineering,127,82-89.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 5th International Conference on Materials Chemistry and Environmental Engineering
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. A Haiyang, Z., Yu, S., Deyuan, L., & Hao, L. (2016). Adaptive neural network PID controller design for temperature control in vacuum thermal tests. 2016 Chinese Control and Decision Conference (pp. 458-463).
[2]. Nguyen, N., & Nguyen, P. (2018). Overshoot and settling time assignment with PID for first‐order and second‐order systems. IET Control Theory & Applications, 2023.
[3]. Li, J., Peng, T., Zhang, S., & Liu, C. (2023). Improved PID Controller Based on BP Neural Network. Journal of Physics: Conference Series, 2479.
[4]. Attaran, S., Yusof, R., & Selamat, H. (2016). A novel optimization algorithm based on epsilon constraint-RBF neural network for tuning PID controller in decoupled HVAC system. Applied Thermal Engineering, 99, 613-624.
[5]. Mao, Q., & Ge, S. (2020). A Parallel Nonlinear Control System of Improved Generalized Predictive Control and Single Neuron PID Based on U-model. 2020 7th International Conference on Information Science and Control Engineering (pp. 1595-1599).
[6]. Nie, L., Jiayi, G., Lu, C., Zheng, H., & Zhishuai, Y. (2018). Longitudinal speed control of autonomous vehicle based on a self-adaptive PID of radial basis function neural network. Iet Intelligent Transport Systems, 12, 485-494.
[7]. Lei, Y., Ma, J., Liu, M., & Liu, P. (2021). Research on Intelligent PID Control Algorithm Based on Neural Network. 2021 International Conference on Intelligent Transportation, Big Data & Smart City (pp. 325-328).
[8]. Li, J., Peng, T., Zhang, S., & Liu, C. (2023). Improved PID Controller Based on BP Neural Network. Journal of Physics: Conference Series, 2479.
[9]. Hameed, A., Karlik, B., & Salman, M. (2016). Back-propagation algorithm with variable adaptive momentum. Knowl. Based Syst., 114, 79-87.
[10]. Lu, H.; Ma, X. & Ye, Y. (2023). Energy coupling control of bridge crane based on adaptive fuzzy strategy. Journal of Physics: Conference Series, 2479, 012055.
[11]. Rodríguez-Abreo, O., Rodríguez-Reséndiz, J., Fuentes-Silva, C., Hernández-Alvarado, R., & Falcón, M. (2021). Self-Tuning Neural Network PID With Dynamic Response Control. IEEE Access, 9, 65206-65215.
[12]. Yang, X., Chen, X., Xia, R., & Qian, Z. (2018). Wireless Sensor Network Congestion Control Based on Standard Particle Swarm Optimization and Single Neuron PID. Sensors (Basel, Switzerland), 18.
[13]. Na, L. (2013). Improved Neural Network PID Controller of Joint Robots. Control Engineering of China, 20.