1. Introduction

Tracking moving targets has become a crucial problem in many domains including robotics, computer vision, surveillance, and autonomous navigation in today's fast evolving technological world. The increasing complexity of modern systems and environments demands more sophisticated tracking solutions that can handle various challenges such as occlusions, noise, and rapid movements. In order to monitor moving targets effectively, researchers must carefully select the right filtering algorithm from a wide array of available options. The problem of choosing the best filters to ensure precise and dependable target tracking frequently confronts researchers, as different scenarios require different approaches. From classical methods like Kalman filters to advanced particle filters and deep learning-based solutions, each technique offers unique advantages and limitations. Therefore, researchers must thoroughly understand the theoretical concepts, implementation requirements, and practical applications of these filtering methods. This understanding is essential for developing robust tracking systems that can perform reliably in real-world applications, where factors such as computational efficiency and accuracy are paramount.

2. The Kalman filters

The choice of filters for tracking moving targets depends on factors like the complexity of the surroundings, the observation system's features, and the target's speed. For linear and Gaussian systems, the Kalman filter is usually the best option. This filter improves the estimation of unknown variables over time by using a sequence of observed data, even if the data includes noise and errors. Introduced by R. E. Kalman in 1960, it has become widely recognized as the standard for optimal estimation [1].

The Kalman filter has been extensively used in the domains of orbit calculation, target tracking, and navigation, including tracking moving targets, GPS location, and orbit computation of spacecraft, due to its real-time, swift, effective, and robust anti-interference properties [2]. Moreover, it is crucial in the domains of sensor data fusion, microeconomics, integrated navigation and dynamic positioning, and, most notably, digital image processing and the hottest areas of research right now, such as pattern recognition. The effect of the Kalman filter is shown in Figure 1.

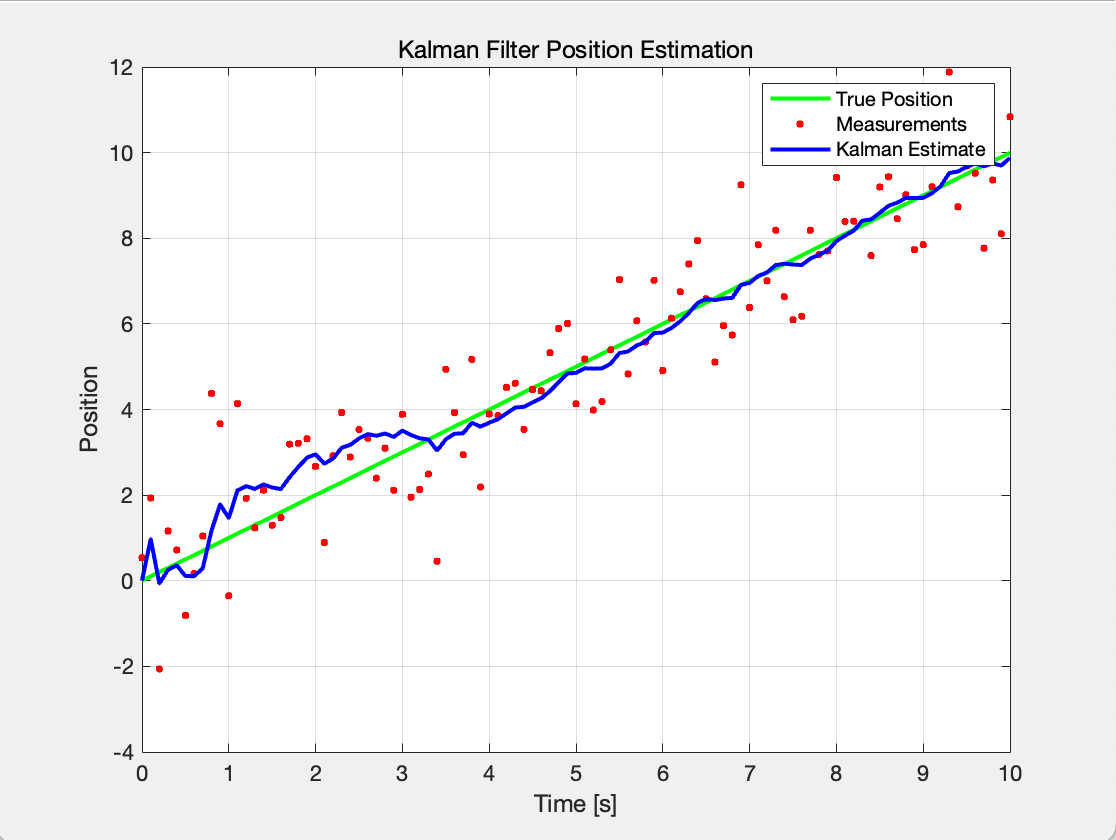
Figure 1: Kalman Filter Position Estimation (Photo/Picture credit: Original).

There are many different types of Kalman filters: the Kalman filter is a variable estimation method for linear systems, known for its ability to minimize variance in estimations. However, KF is also limited in that it can only be used on linear systems and requires Gaussian white noise for the noise. Unfortunately, practically all of the systems are non-linear systems in real life, which limits the use of the conventional Kalman filter, as shown in Figure 2.

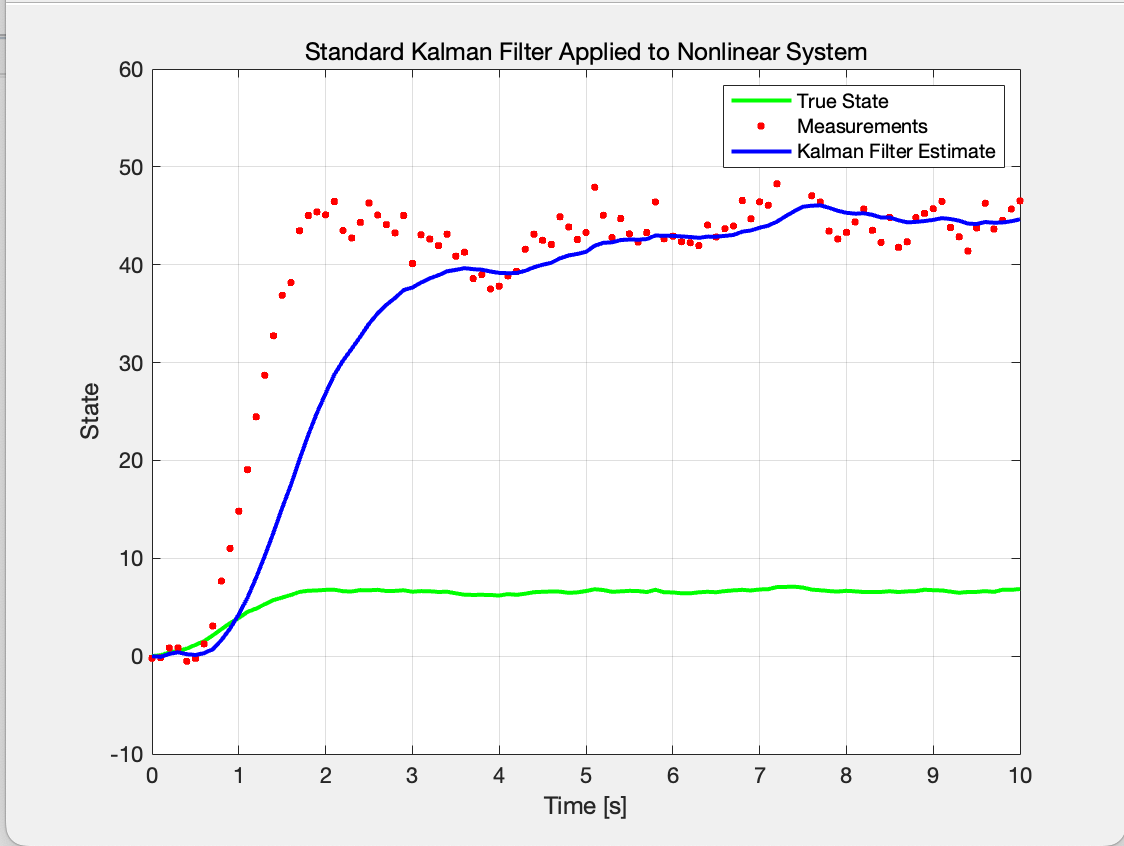
Figure 2: Standard Kalman Filter Applied to Nonlinear System (Photo/Picture credit: Original).

When applied to nonlinear systems, the extended Kalman filter (EKF) linearizes the nonlinear system to the first order in order to approximate filtering. When it comes to target tracking, the EKF works well with somewhat nonlinear systems, like targets that follow intricate routes. The performance of EKF is reliant on status and observation noise. Errors would build if neither of the noise covariance matrices was calculated with sufficient accuracy, leading to divergence in the EKF [2].

In order to increase approximation accuracy, the unscented Kalman filter (UKF), which is also utilized for nonlinear systems, uses the unscented transformation rather than first-order linearization. As a result, the UKF is more suitable for precise target tracking in challenging situations and more stable under highly nonlinear conditions. Because the unscented Kalman filter is more accurate and has a faster convergence rate for solving nonlinear problems, it is closer to the true value of the status system based on statistical features. The square-root Kalman filter, often known as square-root KF, breaks down the covariance matrix into its square root to increase computational accuracy and numerical stability. The square-root Kalman filter might be taken into consideration in target tracking scenarios when computational precision is highly required. Therefore, when researchers decide to use a Kalman filter, they should choose the appropriate type.

A Kalman filter (KF) can be used to represent the beliefs by the moment representation, or the mean and covariance, for a linear Gaussian system (Figure 3). This will result in Gaussian posterior beliefs that are propagated recursively and have closed-form solutions. The extended Kalman filters (EKFs) overcome the linearity limitations by utilizing nonlinear functions to describe both the measurement and the future state probability. This allows them to compute a Gaussian approximation to the real belief [3]. Significant errors in the real posterior are allowed by the EKF, as noted by Wan et al., which may result in less-than-ideal results or even divergence [4]. Subsequently, an alternative to the EKF was proposed: the unscented Kalman filter (UKF), which uses sample points to describe the state distributions [5]. There is polynomial time tracking available for all of the previously described Gaussian filters [6].

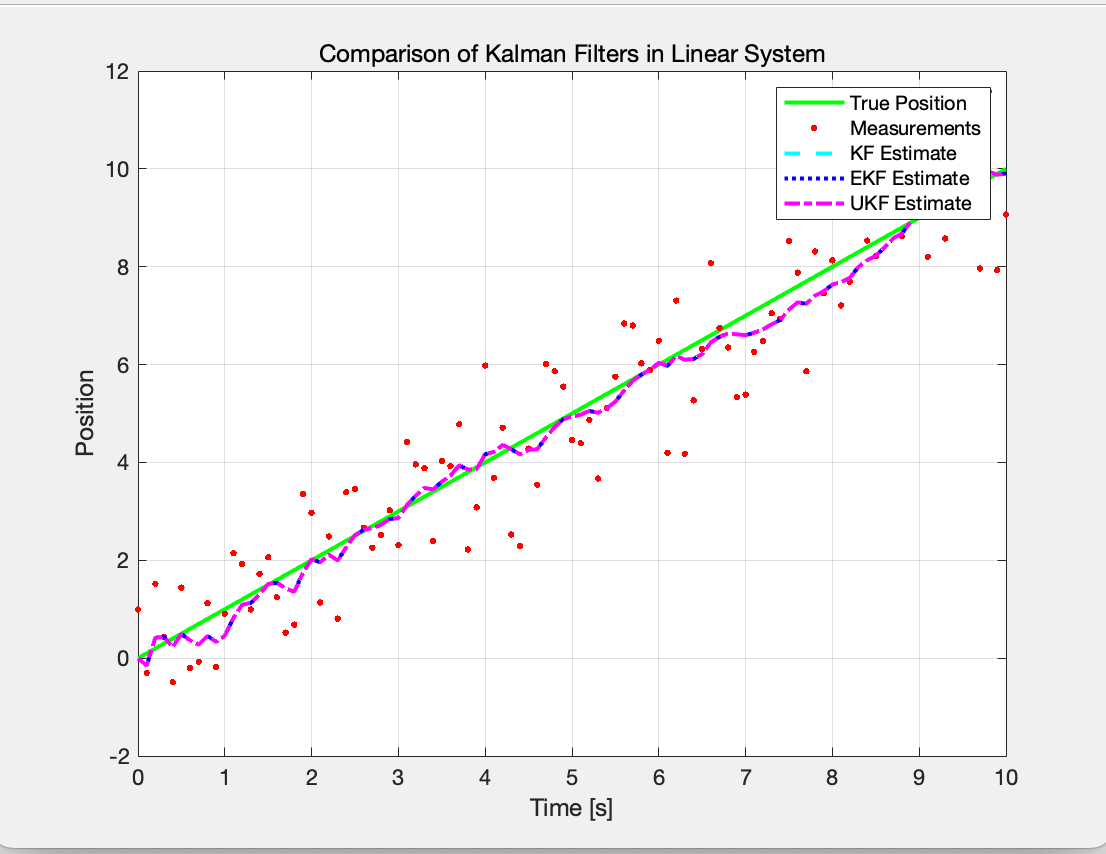
Figure 3: Comparison of Kalman Filters in Linear System (Photo/Picture credit: Original).

3. Particle filter

Particle filters, sometimes referred to as condensation or sequential Monte Carlo, have shown to be effective image tracking techniques in recent years. These approaches' simplicity, adaptability, and methodical handling of nonlinearity and non-Gaussianity are what make them effective [7][8]. The Particle Filter (PF) is a state estimation method designed for nonlinear and non-Gaussian systems. It approximates the probability distribution of the system state using random samples, known as particles. The basic steps of the particle filter:

Initialization: Create a number of particles with equal starting weights to represent potential state. Make a prediction about each particle's future state using the system model as a guide.

Update: Particle weights are updated according to observational data; particles with higher weights correspond to better observations.

Resampling: To prevent degeneration, choose particles according to their weights, retaining heavier particles and eliminating lighter ones.

In this example, the real system is a nonlinear model and the position update contains a sine term: x_true(k) = x_true(k-1) + v * dt + 0.5 * sin(0.5 * t(k)) . This nonlinearity makes the traditional Kalman filter (linear model assumption) a poor estimate of the system state (Figure 4).

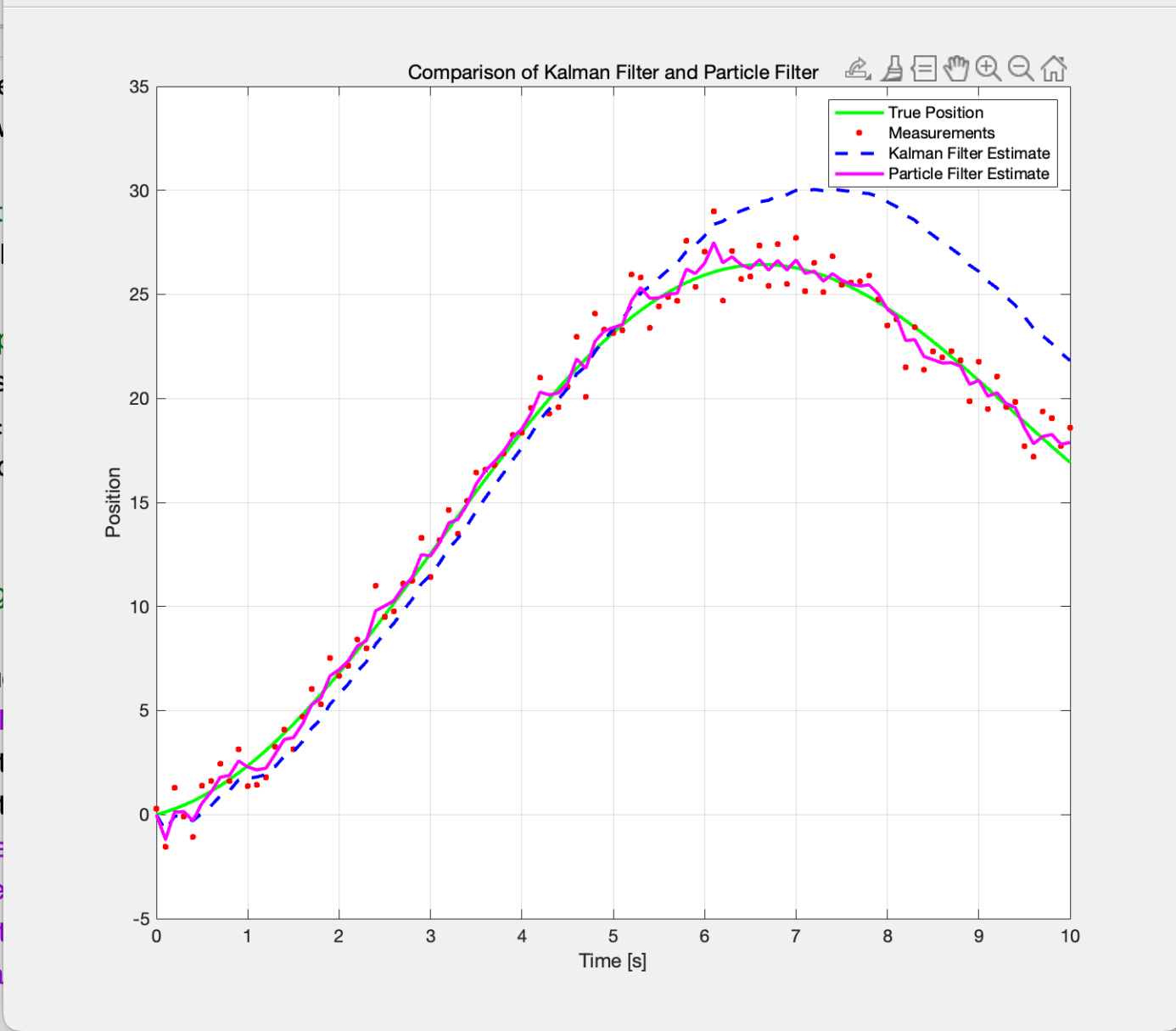
Figure 4: Comparison between the Kalman filter and the particle filter (Photo/Picture credit: Original).

3.1. Statistical model of particle filter

The state sequence {xₜ; t ∈ ℕ}, xₜ ∈ ℝⁿ} is considered in non-Gaussian state-space models to be an unobserved (hidden) Markov process with an initial distribution p(x₀) and a transition distribution p(xₜ | xₜ₋₁), where nₓ is the state vector's dimension. This transition model maps to a typical autoregressive dynamic model in tracking system. Given the process {xₜ; t ∈ ℕ} with marginal distribution p(yₜ | xₜ), where nᵧ is the dimension of the observation vector, the observations {yₜ; t ∈ ℕ*}, yₜ ∈ ℝⁿʸ, are conditionally independent [9].

3.2. Boosted particle filter

There are two significant extensions of the MPF introduced by the boosted particle filter. Initially, Adaboost is used in the proposal distribution creation, which significantly enhances the algorithm's robustness. It is often acknowledged that proposal distributions that take into account the most recent observations-in this paper case, the Adaboost detections-perform significantly better than naive transition prior proposals [10]. Adaboost offers a method for acquiring and preserving the mixture representation, which is the second feature [9]. Once more, this method outperforms the crude K-means clustering algorithm employed in for the same objective. Specifically, it enables us to effectively identify items that are entering and departing the scene [11].

3.3. Adaptive correlation filters

Adaptive correlation filter is a target tracking technology based on correlation filtering. It achieves accurate target tracking by continuously updating and adapting the filter model. The basic idea is to use the similarity between the image features of the target and the template to determine the location of the target through correlation calculations. The working process of the adaptive correlation filter can be summarized into the following steps: Initial training: The system generates a template or filter weight for the target by training a correlation filter within the target area. These weights are obtained by optimizing the associated loss function, usually computed efficiently using a Fourier transform. In each image frame, the correlation filter is applied to the current image area to generate a response map. The position with the highest response value is considered as the likely location of the target. The Adaptive Correlation Filter is a specific form of correlation filter-based tracking used for object tracking. It updates and modifies the filter model continually to accomplish accurate tracking of an object. The primary idea is to use correlation computing to find the target's position based on how comparable the target's and template's image attributes are. Correlation filters, though not widely used, have impressive capabilities. They can track complex objects more than 20 times faster than state-of-the-art methods. This high performance is maintained even in challenging conditions, such as occlusions, rotations, and other distractions [12]. Filter-based trackers use filters that have been trained on sample photos to represent how things appear [12]. A tiny tracking window centered on the object in the first frame is used to determine the target's initial selection. Tracking and filter training now function in tandem. The target is tracked by correlating the filter over a search window in the subsequent frame; the target's new position is indicated by the location corresponding to the maximum value in the correlation output. Based on the updated position, an online update is subsequently carried out.

3.4. Joint probabilistic data association filters

JPDA (Joint Probabilistic Data Association) is a multi-target tracking algorithm designed for complex environments with multiple targets. In these scenarios, the observation data provided by the sensor may match multiple targets, and JPDAF solves the correlation problem between multiple targets and observations by calculating probabilities to improve the accuracy and robustness of target tracking.

3.5. Operating principle

A filter, often a Kalman filter, is used to predict the target's state. This includes predicting the target's next location, speed, and other relevant parameters. Data association: For each frame's observation data, JPDAF associates each observation with the target prediction. It then computes the likelihood of each observation being connected to a distinct target. Joint probability calculation: Taking into account all potential combinations of observation-target pairs, JPDAF computes correlation probabilities based on the target's observed and forecasted positions (joint probabilities). Weight update: Probability weights are used to quantify the likelihood that each observation is connected to a distinct target, and these weights are used to update the target state. State update: JPDAF updates each state's weighted average based on the joint probability. JPDAFs (Joint Probabilistic Data Association Filters) are widely used methods for tracking multiple moving objects simultaneously. They calculate a Bayesian approximation of the relationship between the various items to be tracked and features found in the sensor data. Like most current multi-target tracking methods, JPDAFs employ Kalman filters to estimate the states of individual objects [13].

4. Conclusion

The choice of filter depends on various elements, including system linearity, noise characteristics, processing needs, and environmental complexity. This research investigates four basic filtering approaches for tracking moving targets. Kalman filters: The Kalman Filter (KF) is the best choice for linear systems that have Gaussian noise. These filters improve the estimation of unknown variables over time and handle measurement errors and noise well by processing sequential observed data. Nevertheless, many nonlinear systems in real-world applications do not meet the Gaussian white noise assumption that Kalman filters need, which restricts their usefulness.

Particle filters are employed to overcome the limitations of Kalman filters in nonlinear and non-Gaussian systems. They use a set of random samples, or particles, to approximate the probability distribution of the system state. With the help of this technique, particle filters may systematically tackle challenging tracking jobs and effectively adjust to nonlinearity and non-Gaussianity. Improved versions, such as the enhanced particle filter, significantly increase efficiency and resilience, particularly when tracking objects that are coming into or going out of the scene.

Adaptive correlation filters: These filters provide accurate and fast tracking by continually updating and modifying the filter model. This process is based on the degree of similarity between the visual attributes of the target and a template. They are able to follow complex objects even when there are rotations and occlusions by doing correlation computations. Because of this, they are especially helpful in dynamic settings where the target's appearance may fluctuate. JPDAFs, or Joint Probabilistic Data Association Filters, are intended for multi-target tracking in intricate situations where observations may be related to more than one target. They determine the likelihood that each observation belongs to each target in order to solve the association issue. JPDAFs efficiently handle scenarios with numerous targets and imprecise observations by updating target states based on weighted averages and estimating individual target states using Kalman filters and computing joint probability.

In conclusion, the study emphasizes how important it is to use the right filtering technique for target tracking applications in order to get the best possible performance. To achieve optimal results, the selection of the filtering technique should be tailored to the specific requirements and characteristics of the tracking task.