1. Introduction

The structure of the paper is organized as follows: Chapter 1 presents the introduction, outlining the research background and significance; Chapter 2 details the design process, including the construction of the truth table and optimization of logic expressions; Chapter 3 provides an analysis of delay and power consumption, examining the effects of supply voltage and gate capacitance; finally, the conclusion summarizes the findings of the study.

With the rapid advancement of integrated circuit technology, 4-bit absolute value detectors have found widespread application in signal processing and digital circuit design. These detectors effectively enhance the processing efficiency and reliability of systems[1]. This paper aims to explore methods for improving circuit performance while minimizing delay and power consumption in the design and optimization of a 4-bit absolute value detector, addressing increasingly stringent energy consumption constraints. The study encompasses the design process of the 4-bit absolute value detector, an analysis of delay and power consumption, and the implementation of optimization strategies.

2. Design Process

The initial parameters for the detector are as follows: the minimum energy for a delay that is 50% longer than the minimum delay, the parasitic capacitance is equal to the gate capacitance, CL = 32, VDD = 1 V, and 0 < VDDopt < 1 V.

The primary objective of designing a 4-bit absolute value detector is to compute the absolute value of the input signal. First, the functional requirements of the detector are clarified, which include accepting a 4-bit binary number as input, comparing its corresponding absolute value with a given reference value, and outputting the comparison result. To achieve this goal, the design process is divided into several modules, including the construction of a truth table, simplification of logic expressions, implementation of logic gates, optimization of circuit delay, and identification of the minimum power consumption of the circuit.

2.1. Construct the truth table

Before designing the 4-bit absolute value detector, it is essential to clarify its functionality and operational principles. By analyzing the various combinations of input signals, a corresponding truth table is constructed. The truth table lists all possible input states along with their corresponding output results, ensuring that the design can accurately compute the absolute value. The input signal range is represented as the two's complement of a 4-bit binary number, corresponding to decimal values from -8 to 7.

2.2. Simplify logic expression

Based on the truth table, Karnaugh maps are employed to simplify the logic expressions. The Karnaugh map is a graphical method that effectively reduces the number of terms in the logic expressions [2]. The Karnaugh maps corresponding to S2, S1, and S0 are illustrated in Table 1, Table 2 and Table 3.

The results indicate that the design can be implemented with fewer logic gates, thereby reducing the complexity and power consumption of the circuit. By mapping the truth table, the simplified expressions are as follows:

\( S0=A0 \) (1)

\( S1=A3 \prime A1+A1A0 \prime +A3A1 \prime A0 \) (2)

\( S2=A3 \prime A2+A3A2 \prime +A2A1 \prime A0 \prime \) (3)

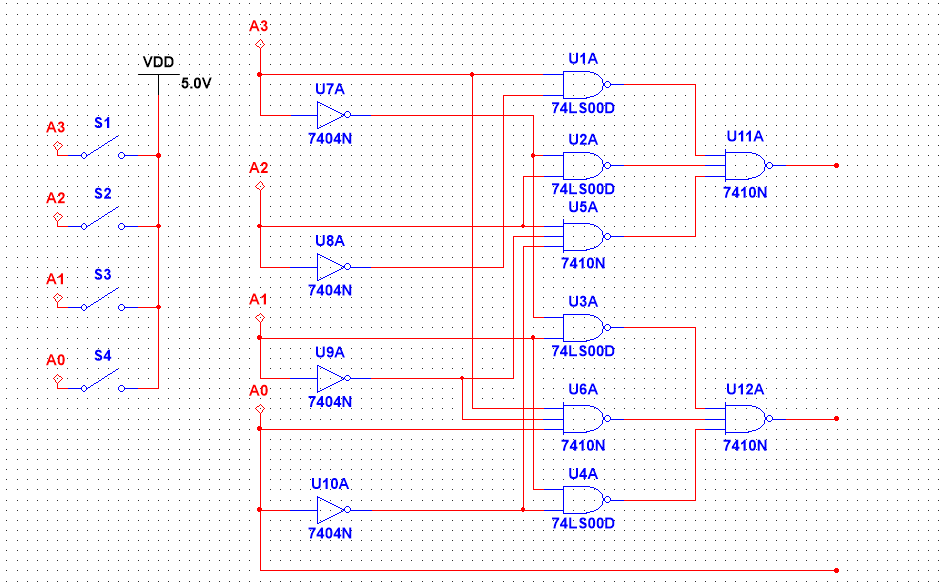
The above expressions will be used for the subsequent circuit implementation, allowing the drawing of the circuit. Figure 1 illustrates the realized circuit structure of the caculater, detailing the connections between various logic gates and their respective functions[3].

2.3. Logic Gate Implementation

In selecting the logic gates, a combination of NAND gates, NOR gates, and inverters was used due to their advantages in delay computation [4]. In this design, all logical functions can be implemented using these gates, eliminating the need for other types of gates and resulting in a more streamlined and analyzable circuit structure [5].

The following section demonstrates how to simplify the logic expressions for the comparator:

\( F=A3B3 \prime +(A3B3+A3 \prime B3 \prime )A2B2 \prime +(A2B2+A2 \prime B2 \prime )(A3B3+A3 \prime B3 \prime )A1B1 \prime \) (4)

\( A3B3+A3 \prime B3 \prime =\bar{A3 \prime B3+A3B3 \prime } \) (5)

\( A2B2+A2 \prime B2 \prime =\bar{A2 \prime B2+A2B2 \prime } \) (6)

2.4. Circuit Optimization

After implementing the preliminary design, circuit optimization was performed to reduce delay and power consumption. By analyzing the critical paths of the circuit, the parts with the most significant delay were identified and specifically optimized to achieve lower delay and power consumption while maintaining circuit functionality.

2.5. Design Verification

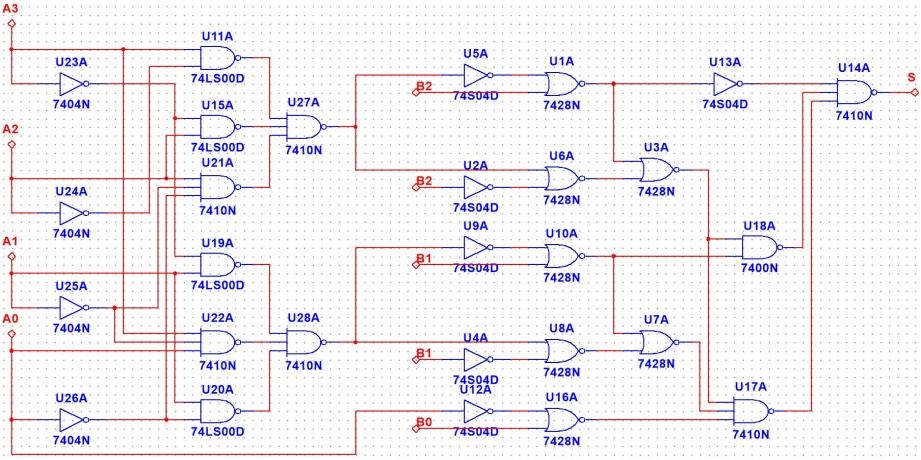
Upon completion of the design, simulation software was used to verify the circuit. Various input conditions were set to observe whether the circuit outputs met the expected results. During the verification process, delay and power consumption under different input conditions were recorded to ensure that the circuit could operate stably in practical applications and meet design requirements[6]. Figure 2 illustrates the overall circuit structure, demonstrating that this logic circuit effectively fulfills its intended function.

3. Delay and Power Consumption Analysis

In the design of circuits, delay and power consumption are two critical performance metrics that directly impact the overall performance and functionality of the circuit. Delay determines the time taken for a signal to propagate from input to output, excessive delay can reduce the circuit's response speed and adversely affect the system's real-time performance. Power consumption relates to the energy efficiency of the circuit. A low-power design not only extends the battery life of devices but also minimizes heat generation, thereby enhancing system stability [7]. Therefore, a comprehensive analysis of both delay and power consumption during the early stages of circuit design is essential to establish effective optimization strategies, ensuring the final product meets both performance and efficiency requirements.

3.1. Delay Analysis

After the design was completed, a thorough analysis of the delay of the 4-bit absolute value detector was conducted. Delay is a critical performance metric in digital circuits, directly impacting the operational speed of the system. By modeling each logic gate in the circuit, the propagation delay from the input signal to the output signal was calculated. The critical path was identified based on the circuit structure; this path represents the segment of signal propagation with the maximum delay[8].

Using the following formula to caculate the total delay:

\( Delay=\sum _{i=1}^{N}({p_{i}}+{g_{i}}×{h_{i}}) \) (7)

Stage effort:

\( {f_{i}}={g_{i}}×{h_{i}} \) (8)

Path electrical effort:

\( {H_{path}}={C_{out}}/{C_{in}} \) (9)

Path logical effort:

\( {G_{path}}=\prod _{i=1}^{N}{g_{i}} \) (10)

Path Delay:

\( D=\sum {D_{i}}=\sum {P_{i}}+\sum {G_{i}}×{H_{i}} \) (11)

In the formulas above, gate delay refers to the delay of each logic gate, while line delay represents the time required for the signal to propagate through the interconnecting lines. By adjusting the supply voltage and the dimensions of the gates, the delay was optimized to maintain the stability and reliability of the circuit within the target delay range.

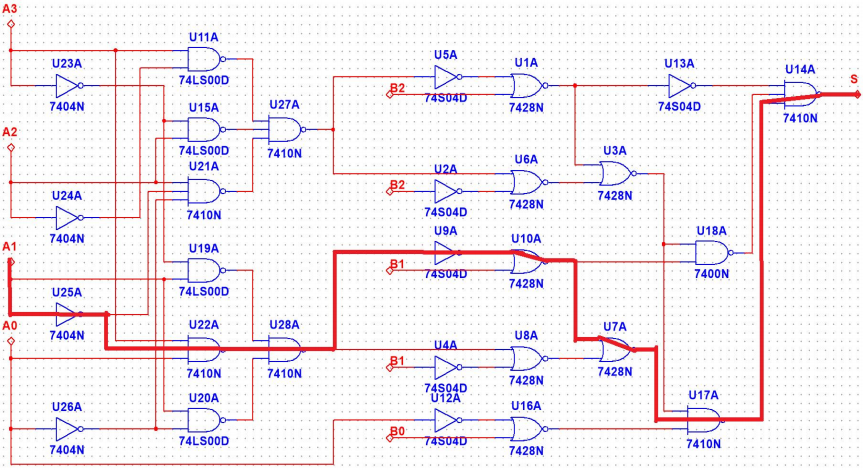
The delay of the critical path in the circuit was first calculated. Figure 3 illustrates the critical path of the circuit, which is the path that traverses the maximum number of logic gates[9].

Table 4 illustrates the stage effort calculated for each logic gate, which is related to the type of logic gate and the number of branches connected to it [10].

Use the formulas below to caculate the size of each gate in the critical path, shown in figure 4.

\( G=\prod _{i=1}^{8}{g_{i}}=g_{inv}^{2}×g_{3NAND}^{4}×C_{2NOR}^{2}={(\frac{5}{3})^{6}},H=32,B=1 \) (12)

\( F=GBH=685.87,f={F^{\frac{1}{N}}}=2.262,{C_{in}}=g\frac{{C_{out}}}{f} \) (13)

3.2. Power Consumption Analysis

Power consumption is another critical consideration in modern digital circuit design. With the advancement of integrated circuit technology, low-power design has become a prevalent trend. Power consumption primarily consists of static power consumption and dynamic power consumption, with dynamic power consumption dominating in most applications.

Assume that Vth=0.2V, the formulas for calculating power consumption are as follows:

\( D=\frac{K{V_{DD}}}{{({V_{DD}}-{V_{TH}})^{2}}} \) (14)

\( 1.5D=\frac{KV_{DD}^{opt}}{{(V_{DD}^{opt}-{V_{TH}})^{2}}} \) (15)

\( E={C_{L}}V_{DD}^{2}=105.67 \) (16)

\( {E_{opt}}={C_{L}}V_{DD}^{{opt^{2}}}=63.48 \) (17)

3.3. Impact of Supply Voltage and Input Capacitance

Analysis revealed that reducing the supply voltage can effectively decrease power consumption; however, it may also lead to an increase in delay. To find a balance between delay and power consumption, the effects of different supply voltage settings and input capacitance values on circuit performance were explored. Increasing input capacitance can reduce delay but may result in higher power consumption. Therefore, it is essential to consider the relationship between these two factors comprehensively during the design process to achieve optimal performance.

3.4. Optimization Strategies

To further optimize delay and power consumption, calculations were performed using MATLAB.

\( {C_{in}}={x^{8}} ,{C_{in}}∈[1,2] \) (18)

\( F=\frac{685.67}{{x^{8}}}, f=\frac{2.262}{x}, {C_{out}}=f\frac{{C_{in}}}{g} \) (19)

\( {C_{ain}}={x^{8}}, {C_{bin}}={x^{7}}, {C_{cin}}={x^{6}}, {C_{din}}={x^{5}}, {C_{ein}}={x^{4}}, {C_{fin}}={x^{3}}, {C_{gin}}={x^{2}}, {C_{hin}}=x \) (20)

\( D=Nf+P=\frac{18.1}{x}+18 \) (21)

Through calculations, it was found that simultaneously adjusting sizing and VDD could achieve minimum power consumption, leading to optimal performance. The implementation of these strategies effectively improved the overall performance of the circuit, ensuring that it met functional requirements while achieving ideal delay and power consumption metrics.

3.5. Result Verification

Finally, the performance of the optimized circuit was verified using simulation tools, recording delay and power consumption data under various supply voltage and input capacitance settings. Experimental results indicate that the optimized circuit achieved significant improvements in both delay and power consumption, providing an effective reference for subsequent designs. The results are listed in Table 5.

4. Conclusion

This study conducted an in-depth analysis of the design and optimization of a 4-bit absolute value detector. Through the construction of a truth table and simplification of logic expressions, the circuit structure was optimized, utilizing NAND, NOR gates, and inverters to achieve an efficient circuit design. In the analysis of delay and power consumption, the impact of supply voltage and internal capacitance was explored, proposing solutions to reduce delay while minimizing power consumption. Experimental results demonstrate that the optimized circuit significantly reduces power consumption while maintaining performance, meeting the demands of modern circuit design. Future research may further investigate adaptability and optimization methods in different application scenarios.