1. Introduction

With the invention of digital computers, the machine simulation of cognitive functions has been a challenging research field for decades. Researchers have spent large amount of effort and resources on this area, including the improvement of algorithms and computational capabilities. However, compared to the traditional digital computer using Boolean logic, digital representations, and clocked operations, the biological nervous system still performs better on various tasks, including pattern recognition, sensory processing, and motor control. Specifically, the biological nervous system carries out robust and reliable computation using hybrid analog/digital unreliable processing elements; They emphasize massively parallel, event- driven, collective, highly adaptable and flexible, and make extensive use of adaptation, self-organization and learning [1]. Additionally, Moore’s law is going to its end [2]. It seems a new type of computer system should be proposed and used in the future other than the computer with the Von Neumann architecture. The future of neuromorphic computing is more promising.

This paper first explains the basic dynamic and math embed in the cognitive systems. Then the author introduces the basic structure of neuromorphic computing. And then the paper explains and evaluates the advantages and disadvantages of researchers’ different methods to approach and simulate the autonomous cognitive system. The purpose of this paper is to compare different scholars’ work in order to propose a possible future for a more efficient cognitive system based on CMOS.

2. Neural dynamics

It would be important to introduce the basic principles behind animals’ cognitive systems. Even though nowadays there is a large amount of investigation into how mammals’ brain function, there are still a lot of things unknown for us. If we don’t know exactly how the nervous system works, in other words, how to compute, we cannot precisely simulate the cognitive process. However, we do know a lot about how our brains deal with information. We could focus on several important structures and their mechanisms first. They are neurons and synapse, the basic structure of cognitive system. First of all, the input of a neuron is an active potential, or “spikes”. An impulse would be the input to the neuron. When the active potential (membrane potential) is higher than the threshold value, an impulse or multiple impulse would be injected. The impulse will be transmitted through a synapse between the postsynaptic neuron and presynaptic neuron. The mathematical principle embed of mechanism of neuron and synapse has now been investigated clear enough for simulating [3].

It would be important to recognize the math behind the Spike trains and their dynamical models. Spikes is a series of impulses, and a single impulse is described as the following delta function:

\( p(t)=\sum _{i=0}^{k}δ(t-{t_{i}})\ \ \ (1) \)

Considering the existence of the noise caused by various factors and that each spikes happens independently (thus each event happened randomly), the generation of spikes could be simulated as Poisson distribution. Given the time of \( Δt \) , the probability of n spikes happening is:

\( P(n)= \frac{{e^{-rt}}}{n!}{(rt)^{n}}\ \ \ (2) \)

Now we have the basic math model for spikes. For membrane potential, its increasing variables rises faster than its recovery variables. In order to faithfully simulate the real-time process of membrane potential, we have to consider about both increasing factors and recovery factors. Eugene Izhikevich proposes a first order differential equation for the simulation:

\( \frac{dv}{dt} = a{v^{2}}+bv+o+I\ \ \ (3) \)

\( \frac{du}{dt} = k(pv-u)\ \ \ (4) \)

\( if v≥{v_{peak}}, then c→v, g+d→g.\ \ \ (5) \)

Here, u and v are dimensionless variables, k, p, c, d are dimensionless parameters, and t is time. I is the synaptic currents went through the coma. With these basic equations and the emergence of nano-scale memrisive devices, a neuromorphic circuit for stochastic learning behavior would be possible to design. Memrisive devices could be integrate with CMOS chips [4]. They have to be non-volatile and have a nano-scale footprint. Scholars have developed CMOS for different tasks of learning, which will be discussed in the 3rd chapter [5].

3. The history and development of Neuromorphic computing

Neuromorphic computing was first proposed by Caltech professor Carver Mead in 1980 [6]. Mead proposed an analog silicon retina, which foreshadowed a new type of physical computations. Specifically, he invented floating-gate analog structures, which could store charge for a long period of time. This helped to solve the big problem for silicon neural network: everytime the networks were switched off, the charges were lost and the network would ‘forget’ the tasks they had learned. What Mead has invented help to solve this problem. More importantly, it would be possible then to design an analog circuit in order to mimic some of the functions of a real brain including the function of the retina. The first silicon neuron in the true sense is invented by Misha Mahowald and Rodney Douglas in 1991 [7]. They invented an analog circuit with the functions of real nerve cells. Specifically, based on the similarity of the conductivity of biological membranes and silicon, a silicon neuron could simulate the rapidly raising or decreasing membrane potential, which means that silicon neuron could emulate the iron currents causing nerve impulses. Many silicon neurons could be fabricated on a single silicon chip. This silicon neuron represents a step toward constructing artificial nervous systems. From then, plenty of neuromorphic chips have been invented including ARMbased simulated spiking neural networks (SpiNNaker) [8], Asynchronous simulation of neurons and synapses (Loihi) [9], Large-scale asynchronous spiking neural network (TrueNorth), Wafer-scale analog neural accelerators (BrainScaleS) [10], Real-time neuromorphic large-scale system (BrainDrop) [11], Real-time on-line learning neuromorphic chips (DYNAPs) [12]. They each are designed for different purpose and based on different ideas. For example, DYNAPs is a full custom analog/digital models of cortical circuits. And it is designed for implementing principles of neural computation in real-time behaving agents [12]. BrainScaleS is full custom large-scale analog/digital neural processing system, and it is designed for faithful reproduction of neuroscience simulations [10]. More recently, some new neuromorphic chips for different purpose is invented including Tianjic by Tsinghua University [13], Akida by Brainchip [14], GrAIOne by GrayMatterLabs [15], etc. As said above, different chips are designed for different purpose of using. For example, Tianjic is made for autodrive.

4. Recognition system

4.1. Early effort and development

Pattern recognition is one main field researchers focus on. There are already plenty of researchers developing models for machines to learn the patterns of specific graphs. Most researchers are focusing on using computer with traditional digital computers. In 2012, Geoffrey Hinton’s team posted AlexNet based on Convolutional Neural Network [16]. There are also other researchers who are focusing on using the technology of neuromorphic computing to make computers recognize patterns. In the past 20 years, with the invention of nano-scale memristive devices, it has become possible to design a circuit with complex and powerful computational properties, which is the same as a synapse’s computational properties. Nano-scale memristive devices offer a compact and efficient solution to modeling synaptic weights, and they could be integrated with Complementary Metal-Oxide Semiconductor (CMOS) chips. Indeed, to simulate some basic dynamical properties such as neurons and synapse, analog CMOS has been effectively employed on the simple neuromorphic circuits. In 1999, Timothy K. Horiuchi and Christof Koch described a neuromorphic system that could simulate the physical dynamics of the oculomotor system [17]. Other researchers have also done similar work. Ad hoc approaches were used to create these systems, however they were only able to implement relatively precise sensory-motor mappings or capabilities. Horiuchi and Koch design a read time modeling system to solve the tasks in the real world by an osculator system constructed using two different VLSI chips: One is for the mimicking the visual process of selecting the target, and the other is to simulate the muscle which drive the eye movement. However, they only use a single object as a target for their osculator system to recognize and capture. Horiuchi and Koch’s systems cannot keep track of multiple different objects moving together. The remaining task is to construct fully functional neuromorphic acting systems with cognitive capabilities using reactive artificial neural modules. In neuromorphic systems, the transition from reactivity to cognition is not simple because the fundamentals of cognition have not yet been fully understood. The formalization of these concepts and their successful use in hardware are currently active research areas. The construction of brain like processing systems able to solve cognitive tasks requires sufficient theoretical grounds for understanding the computational properties of such a complex system and effective methods to combine these components in neuromorphic systems. Researchers have worked toward this objective over the past 10 years by creating neuromorphic electronic circuits and systems and using them as the foundation for the creation of straight forward neuromorphic cognitive systems. These building blocks works similarly consider their translinear loop. As an example, the DPI circuit would be discussed in the next section [18].

4.2. DPI circuit

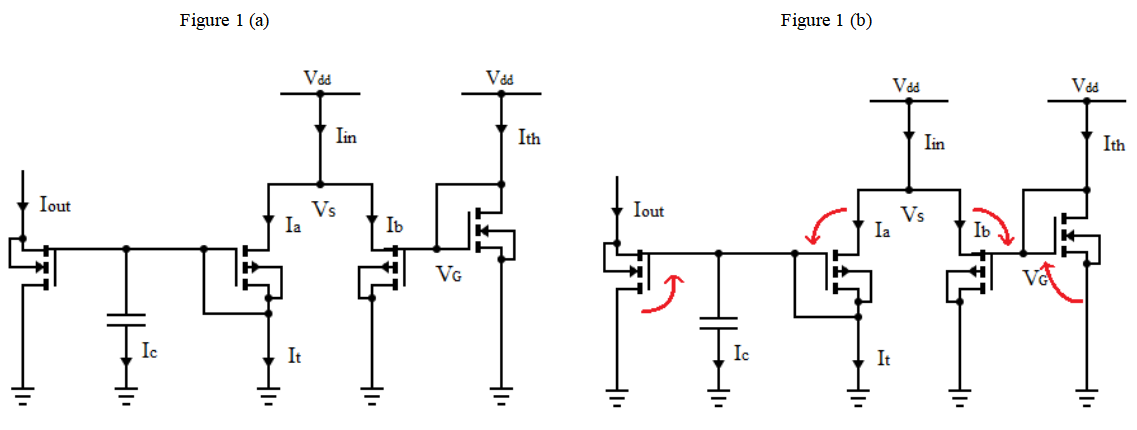
Since DPI circuit is introduced to implement both synapse and neuron models, it would be discussed first.

Consider the DPI circuit showed in Fig1. It is constructed by several n MOSFET and p MOSFET. The current-voltage characteristic can be expressed as multiplication of the current flowing across each transistor. We have:

\( {I_{out}}={I_{0}}{e^{\frac{k{V_{c}}}{{U_{t}}}}}\ \ \ (5) \)

\( {I_{c}}=C\frac{d{V_{c}}}{dt}\ \ \ (6) \)

\( {I_{in}}={I_{1}}+{I_{τ}}+{I_{c}}\ \ \ (7) \)

\( {I_{c}}=C\frac{{U_{T}}}{k{I_{out}}}\frac{d{I_{out}}}{dt}\ \ \ (8) \)

Here \( {U_{t}} \) represents the thermal voltage. \( {I_{d}} \) represents the dark current. k represents the subthreshold slope factor. And based on the translinear loop in the graph, for currents, there exists:

\( {I_{th}}({I_{in}}-{I_{τ}}-{I_{c}})=({I_{τ}}+{I_{c}}){I_{out}}\ \ \ (9) \)

Combining Equation 5-8 with Equation 9, the solution would be:

\( τ\frac{d{I_{out}}}{dt}+{I_{out}}=\frac{{I_{th}}}{{I_{τ}}}{I_{in}}\ \ \ (10) \)

\( τ=\frac{C{U_{T}}}{k{I_{τ}}}\ \ \ (11) \)

With DPI, LPF, and Tau-cells’ first order differential equation, a neuron’s basic dynamics and the transmission of information through synapse can be mathematically modeled. Then it would be possible to construct silicon neurons and synapses with these circuits [18].

Although building a cognitive system using noisy and inhomogeneous subthreshold analog VLSI constructed by the building blocks discussed above is very difficult, scholars have figured out different effective ways to build autonomous recognitive systems.

4.3. Recognitive system based on neuromorphic electronic circuits

Some scholars construct VLSI based on the building blocks above for the cognition system of sensory- motor processes. In 2013, Schöner constructed a neuromorphic network for the sequence generation of sensory-motor processes [19]. Using DPT, Schoner and his co-workers constructed a system that could recognize a sequence of actions. However, this system could only recognize different objects with different colors and manage its actions on these objects. If objects were changed into more complicated objects, the system wouldn’t be stable. The system Schöner created are still immature. But there is still something very advanced in this idea: The systems they created are highly noise-tolerated. The system can recognize the object and decide by itself.

Instead of focusing on designing a recognitive system for the machine to solve a specific given task, multiple scholars are working on a recognition system that could recognize and learn different objects. In other words, a general system that could solve more complicated problems happened in the real world.

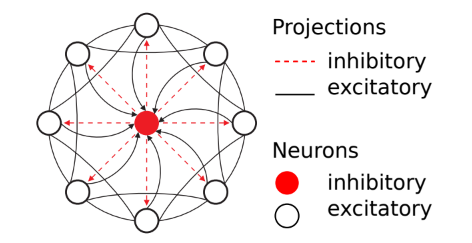
Some scholars use silicon neuron to construct recurrent neural networks that could produce context-dependent behavioral responses. In 2014 Sep 9, E Chicca, F Stefanini, Chiara Bartolozzi, and G Indiveri described some neuromorphic electronic circuits and systems for the realization of simple neuromorphic cognitive systems [20]. They used a soft Winner-Take-All (sWTA) network based on the artificial neural network (ANN) model: sWTA network is constructed by inhibitory neurons and excitatory neurons. It is constructed by the connection between synapse, inhibitory neurons and exhibitory neurons as shown in the Figure2. In response to an input stimulus, these neurons would compete against one another. The “winner”, the one with the highest response, would win the competition. It is so called the Soft Winner take all. They also constructed the chip using silicon neurons. Note that the AER input block used in the circuit uses a new asynchronous communication standard that allows VLSI neurons to use the impulse as an input. In this paper, scholars also do some experiments using these circuits. For example, scholars send a Poisson spike train of 55 HZ passion as a representation of the input pattern to the synapse, and the Poisson impulse would be sent to the exhibitory neurons, store in the memory, and generate the highly irregular dynamics of \( {V_{mem}} \) through the synaptic states. As a result, the circuits would gradually generate the pattern like the input pattern. What’s important in their work is that they propose a simple, low-power, and compact solution for an autonomous cognitive system. The idea of the circuits and networks they design is used in other scholars’ work to build autonomous cognitive systems for different purposes. This work, including the system of circuits and algorithms designed by Giacomo and his coworkers, provides the basis for more advanced recognitive system. They design a VLSI which is low energy consumed and highly efficient. It provides an example of the basic frame to construct a more complicated recognitive system for the real world tasks. More importantly, it recognizes different patterns in random noise.

However, the results Giacomo and his coworkers get in the experiment in their paper could be possibly improved by improving the algorithm. Specifically, they could set the Input frequency- Output frequency to be different functions. Instead of the ReLu activation function of ANN, there are other functions available such as sin functions or sigmoid functions. And also, the DPI neuron used in the article can be placed in different weights in order to maximize the output frequencies.

5. Conclusion

This paper introduces the math simulation of the neural dynamics, the history and development of recognitive systems, advantages and disadvantages of multiple scholars’ work, and some possible improvement of the recognitive systems. Based on the work done by multiple scholars, one potential improvement of the recognition system would be changing the structure of the memory system. As an example, we could create a random process for the system to “forget” value at some moment based on the random mask process. It might make the recognition system to be more flexible and robust at some given circumstance. It would be important to note that, the limitation still exist: the research nowadays is still not robust enough to solve the task in the real world. This paper propose that based on the work multiple scholars have done, a complex system containing robust algorithms and sophisticated circuit (especially the design of memory circuit) is needed in order to construct a reliable recognition system in the future. Until now, compared to the conventional standard engineering and technology fields, the rate of progress in the neuromorphic engineering area has been disappointingly slow. But with investment of the company and multiple companies, the area of Neuromorphic Engineering has a promising future. And also, with the development of ground theory of neuroscience, the simulation of the recognitive system in the brain would be more precise and thus better.