1. Introduction

With the rapid development of display technology, thin-film transistor liquid crystal display (TFT-LCD) has become a mainstream display technology and has been widely used in smart phones, TVs, laptops and other devices[1]. The quality of its display effect directly affects the user experience of terminal devices, and the quality of TFT-LCD is affected by a variety of production processes and material characteristics[2]. Traditional quality prediction methods usually rely on manual experience or rule-based detection methods. Manual detection is inefficient and subjective, and is easily affected by the experience and status of the inspector; traditional rule-based models lack robustness to changes in the production environment and are difficult to adapt to complex and changing industrial scenarios. With the accumulation of industrial data and the improvement of computing power, intelligent prediction methods based on machine learning have gradually become the main means to solve the problem of TFT-LCD quality prediction. However, TFT-LCD production data usually has high-dimensional features, multivariate nonlinearity and strong correlation. It is often difficult to achieve good results by directly applying traditional machine learning models[3].

Feature selection is an important step in solving high-dimensional data problems. By selecting the most critical features for the target variable from a large number of redundant or irrelevant features, the data dimension can be effectively reduced and the performance and generalization ability of the model can be improved. Among them, the feature selection method based on L1 regularization can directly compress the weights of unimportant features to zero due to its sparsity constraint ability, thereby realizing automatic feature selection. In terms of model design, ensemble learning and deep learning methods have been widely used in quality prediction tasks in recent years[4]. Gradient boosting decision tree[5] (such as XGBoost) has become one of the mainstream models in the industry due to its modeling ability and efficiency for feature importance; multi-layer perceptron (MLP)[6] in deep learning can capture the complex nonlinear relationship of data. Combining the advantages of these two types of models, the MLP-XGBoost ensemble model was proposed to simultaneously extract deep features and model complex decision boundaries, providing a new technical approach to solving complex industrial prediction problems. However, the hyperparameter tuning of the ensemble model faces great challenges in large-scale industrial data. Traditional grid search or random search methods are inefficient and difficult to meet actual needs. In recent years, optimization algorithms based on swarm intelligence, such as genetic algorithm (GA) and particle swarm optimization (PSO), have shown great potential in model optimization. Among them, the Salp Swarm Algorithm (SSA) [7] has gradually become an effective tool for hyperparameter optimization due to its strong global search capability and fast convergence characteristics.

2. Method

In order to better predict the quality of TFT-LCD, this paper proposes a model framework based on L1 regularized feature selection, SSA optimization and MLP-XGBoost fusion, which can be divided into three key modules: feature selection module, hyperparameter optimization module and regression prediction module. The algorithm flow is shown in Figure 1.

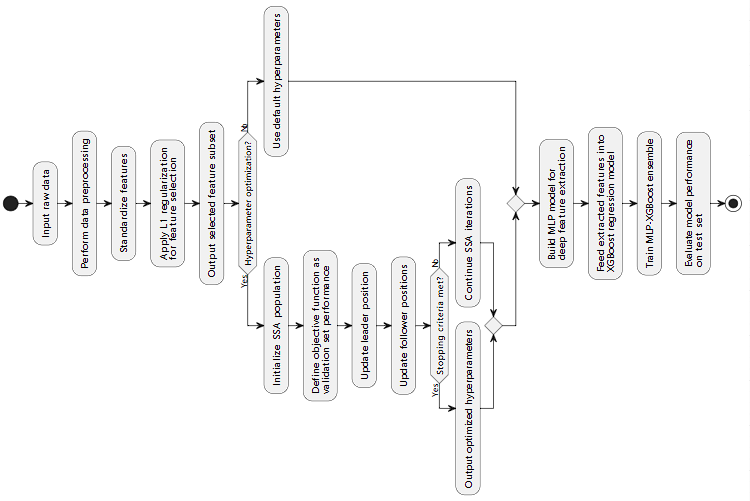
Figure 1: Algorithm flow

2.1. Embedded method based on L1 regularization

In TFT-LCD quality prediction, a large amount of data is usually involved, and these features may have significant redundancy or correlation. High-dimensional feature data will not only increase the computational complexity of model training, but may also reduce the generalization ability of the model, leading to overfitting problems. Therefore, feature selection is a key step in building an efficient regression model. L1 regularization is an embedded feature selection method that removes irrelevant features through sparse constraints while retaining the features that have the greatest impact on the target variable. Taking linear regression as an example, its objective function can be expressed as follows after adding the L1 norm constraint:

\( {min_{w}}(\frac{1}{2n}{\sum _{i=1}^{n}{(y_{i}}-{X_{i}}w)^{2}}+λ||w|{|_{1}})\ \ \ (1) \)

Where: n is the number of samples; \( {y_{i}} \) is the target variable of the i-th sample (such as the brightness value of TFT-LCD); \( {X_{i}}∈{R^{m}} \) is the feature vector of the i-th sample (containing m features); \( w∈{R^{m}} \) is the model parameter vector; \( λ \gt 0 \) is the regularization strength, which is used to control sparsity. By adjusting the regularization strength \( λ \) , the sparsity and fitting ability of the model can be balanced. The feature selection process is as follows:

(1) Data standardization: In order to ensure the consistency of the scale of different features, the feature matrix X is first standardized so that the mean of each column feature is zero and the variance is one.

(2) Model training: Construct an L1 regularized linear regression model, take the target variable y as the predicted value, and minimize the objective function with L1 regularization.

(3) Weight sparsification: After training, observe the model weight vector w. For the feature \( {x_{j}} \) of \( {w_{j}}=0 \) , it is determined that it has no significant effect on the target variable and the feature is removed.

(4) Result generation: Output the features of weight \( {w_{j}}≠0 \) to generate the feature subset \( {X_{selected}} \) after dimensionality reduction.

After the above steps, the feature selection module can effectively reduce the data dimension, retain the features with the highest correlation with the target variable, and provide a concise and efficient data foundation for subsequent modeling.

2.2. Global optimization strategy based on SSA

We selects MLP (multi-layer perceptron) and XGBoost (extreme gradient boosting) to construct a regression model for TFT-LCD quality prediction, mainly based on the complementarity of the two in feature processing and regression performance. MLP has strong nonlinear modeling capabilities through its multi-layer network structure and activation function. It can extract deep features from complex high-dimensional data and map redundant features into a more compact and discriminative representation. On the other hand, XGBoost is based on gradient boosting decision trees, is good at processing complex nonlinear decision boundaries, and has high robustness to noise and outliers.

The hyperparameters of MLP and XGBoost have an important impact on model performance. However, traditional grid search and random search methods are inefficient in searching in high-dimensional parameter spaces, and finding the global optimal solution is difficult. This paper uses SSA (Salp Swarm Algorithm) to optimize the model's hyperparameters. SSA is an optimization algorithm based on swarm intelligence, which completes the global search by simulating the movement behavior of willow leaf fish. The algorithm realizes the dynamic optimization of the objective function through the collaboration of individuals in the population.

(1) Population initialization: Let the population size be N, and each position represents a set of hyperparameter vectors \( {x_{i}}=[{p_{1}},{p_{2}},…,{p_{d}}] \) , where d is the hyperparameter dimension. The initial position matrix is:

\( X=[\begin{matrix}{x_{1,1}} & {x_{1,2}} & ⋯ & {x_{1,d}} \\ {x_{2,1}} & {x_{2,2}} & ⋯ & {x_{2,d}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ {x_{N,1}} & {x_{N,2}} & ⋯ & {x_{N,d}} \\ \end{matrix}]\ \ \ (2) \)

(2) Individual update rule:

The individual with the best objective function value is selected as the leader. The leader position update formula is:

\( x_{leader,j}^{(t+1)}=x_{leader,j}^{(t)}+{c_{1}}{r_{1}}({x_{target,j}}-x_{leader,j}^{(t)})\ \ \ (3) \)

Where \( {c_{1}} \) is the scaling factor, \( {r_{1}}∪(0,1) \) is a random number. The positions of other individuals are dynamically adjusted based on the leader:

\( x_{i,j}^{(t+1)}=\frac{x_{i-1,j}^{(t)}+x_{i,j}^{(t)}}{2},i≥2\ \ \ (4) \)

(3) Constraint processing: If the individual exceeds the hyperparameter range, it will be reinitialized.

(4) Stop condition: Optimization is terminated when the maximum number of iterations is reached or the objective function value converges.

2.3. MLP-XGBoost integrated modeling

The MLP-XGBoost integrated model combines the nonlinear feature extraction capability of deep learning and the regression prediction capability of XGBoost. Its overall structure is divided into two stages:

(1) MLP feature extraction: MLP consists of an input layer, a hidden layer, and an output layer, and generates high-dimensional feature representations through multiple layers of nonlinear transformations. The hidden layer output formula is:

\( {h^{(l)}}=f({W^{(l)}}{h^{(l-1)}}+{b^{(l)}})\ \ \ (5) \)

Where \( {W^{(l)}} \) and \( {b^{(l)}} \) are the weight matrix and bias vector, respectively, and \( f(∙) \) is the activation function.

(2) XGBoost regression prediction: The features generated by MLP are input into XGBoost, and the target variable is predicted using the gradient boosting decision tree. The objective function of XGBoost is:

\( L=\sum _{i=1}^{n} l({\hat{y}_{i}},{y_{i}})+\sum _{k=1}^{K} Ω({f_{k}})\ \ \ (6) \)

Where \( l(∙) \) is the loss function, \( Ω({f_{k}}) \) is the regularization term of the tree.

The integration process can be summarized as: using MLP to perform deep feature extraction on feature-selected data; inputting the extracted features into XGBoost to model the complex relationship between features and target variables; and finally outputting the predicted value \( \hat{y} \) .

3. Experimental analysis

3.1. Dataset and Experimental Settings

This study experimentally verifies the performance of the proposed MLP-XGBoost integrated model based on L1 feature selection and SSA optimization in the TFT-LCD quality regression prediction task. The experiment uses TFT-LCD production data collected from industrial production lines. The data set contains thousands of sample records, each of which corresponds to the process parameters and quality indicators of a TFT-LCD product, totaling 5000 data, 50 original features, and the target variable is TFT-LCD brightness (unit: cd/m²). The data set is randomly divided into training set, validation set and test set in a ratio of 7:2:1 for model training, hyperparameter tuning and performance testing. In order to ensure the fairness of the experiment, all features are standardized so that the mean of each feature is 0 and the variance is 1. In addition, the brightness value of the target variable is normalized so that its distribution range is scaled to [0,1]. In order to comprehensively evaluate the regression performance of the model, this paper uses the following three common indicators:

Mean Squared Error (MSE):

\( MSE=\frac{1}{n}\sum _{i=1}^{n}{(\hat{{y_{i}}}-{y_{i}})^{2}}\ \ \ (7) \)

Root Mean Squared Error, (RMSE):

\( RMSE=\sqrt[]{MSE}\ \ \ (8) \)

Coefficient of determination(R2):

\( {R^{2}}=1-\frac{\sum _{i=1}^{n}{(\hat{{y_{i}}}-{y_{i}})^{2}}}{\sum _{i=1}^{n}{({y_{i}}-\bar{y})^{2}}}\ \ \ (9) \)

3.2. Comparison model

In order to verify the effectiveness of the proposed method, the following classic models and their variants are selected for comparison. (1)Linear Regression (LR): A simple linear regression method as a baseline model. (2)Support Vector Regression (SVR): A kernel function-based regression method for dealing with nonlinear problems. (3)Random Forest Regression (RF): An integrated model based on decision trees that is good at dealing with high-dimensional nonlinear data. (4)XGBoost: An efficient gradient boosting decision tree model widely used in industrial prediction tasks. (5)MLP: A multi-layer perceptron model in deep learning, used to extract complex nonlinear features of data. (6)MLP-XGBoost (unoptimized): An integrated model combining MLP and XGBoost, but without SSA hyperparameter optimization. The following are the performance results of different models on the test set, as shown in Table1.

Table 1: Performance comparison of different models

Traditional linear regression and SVR methods have limitations in nonlinear feature modeling and poor prediction performance; Random forest and XGBoost models have better performance than traditional methods due to their good modeling ability for nonlinear features; MLP can capture complex nonlinear relationships, but due to the limitations of hyperparameter settings, its performance is not as good as that of the integrated model; The unoptimized MLP-XGBoost integrated model is worse than either MLP or XGBoost alone, indicating that the combination of the two has a synergistic gain effect; The model in this paper performs best in all evaluation indicators, verifying the contribution of L1 feature selection and SSA optimization to performance improvement.

3.3. SSA hyperparameter optimization effect

In order to verify the effect of SSA on hyperparameter optimization, the performance of the model before and after SSA optimization is compared, and the results are as follows, as shown in Table 2.

Table 2: Performance of hyperparameter optimization

The results show that SSA optimization significantly reduces the prediction error of the model and improves the model's fitting ability. Through experimental analysis, the MLP-XGBoost integrated model based on L1 feature selection and SSA optimization proposed in this paper performs well in TFT-LCD quality regression prediction. The experimental results verify the effectiveness of L1 feature selection for dimensionality reduction and feature extraction, the significant contribution of SSA to hyperparameter optimization, and the synergy of MLP and XGBoost in complex data modeling.

4. Conclusion

This study proposes a new framework for TFT-LCD quality regression prediction by integrating L1 feature selection, SSA-based hyperparameter optimization, and MLP-XGBoost ensemble modeling. Experimental results on real-world TFT-LCD production data show that the proposed model outperforms traditional machine learning methods and unoptimized models, achieving superior accuracy and reducing prediction errors.