1. Introduction

1.1. Background

Warehouse robotics is gradually being embraced by small and medium-sized businesses as technology develops and society advances, and e-commerce and online shopping proliferate, leading to a demand for efficient warehouse operations [1]. Traditional warehouse management relies on a large number of manual labors to handle, sort and manage goods, resulting in high labor costs, low efficiency and slow speed of manual handling and sorting in the warehouse. In the process of manual operation, there may be goods falling, equipment failure and other safety hazards. With the progress of society, warehouse automation gradually replaces manual labor [2]. In today's society, problems such as low computational efficiency, long waiting time for robots, and collision of multiple robots occur frequently in warehouse management, making warehouse transportation extremely inefficient.

Many traditional methods, such as the A* algorithm, can achieve good results in warehouses with fewer fixed obstacles in the number of goods and fewer mobile warehouse robots. However, as the number of fixed obstacles increases, the timeout problem becomes serious when the A* algorithm is applied to path planning for multiple warehouse robots. Compared with the A* algorithm, the RRT* algorithm is more advantageous in solving complex obstacles [3]. In each expansion step of the RRT* algorithm, the algorithm not only expands the nodes of the tree, but also tries to optimize the path by reconnecting existing nodes. This greatly improves the efficiency in dealing with multiple stationary obstacle problems.

The CBS algorithm is a widely used multi-robot path planning algorithm that finds optimal paths for multiple warehouse robots by resolving their optimal path conflicts [4]. The basic method is to plan the optimal path for each warehouse robot individually, if there is a conflict between the optimal paths of warehouse robots, CBS will generate child nodes, then calculate the global cost function of each child node, and then find the node with the smallest cost in the whole constraint tree [5]. This process is repeated until a path is found where all robots can reach their destinations safely. By this method, CBS can effectively deal with the conflict problem among multiple robots and find the global optimal solution [6]. Therefore, compared to the CBS algorithm and the A* algorithm, this thesis combines the RRT* algorithm with the CBS algorithm with the aim of improving the algorithmic runtime for warehouse robots facing complex obstacles. The difference between this algorithm (RRT* algorithm combined with CBS algorithm) and the traditional algorithms available in the market (A* algorithm combined with CBS algorithm) is that the RRT* algorithm referenced in this algorithm is progressively optimized, and with the increase in the number of iterations and sampling points, the obtained paths will be optimized accordingly, and thus the path planning time is shorter compared to the traditional algorithm (A* algorithm combined with CBS algorithm). Shorter path planning time. This algorithm (combination of RRT* algorithm and CBS algorithm) can be applied to the real problem of warehouse robotics, where warehouse robot path planning is faced with multiple robots and multiple obstacles.

1.2. Proposed idea

Conflict-Based Search (CBS) and Rapidly-exploring Random Tree Star (RRT*) are prominent algorithms used in robot path planning, each addressing different aspects of the problem. CBS is designed for multi-agent path planning, focusing on coordinating several agents navigating through a shared environment. It operates by initially finding a coarse solution that may have conflicts between agents and then iteratively resolving these conflicts through a high-level search strategy. This involves adding constraints to the problem and using a low-level path planning algorithm, such as A* or Dijkstra's, to find feasible paths that adhere to the new constraints [7]. The iterative nature of CBS helps in efficiently finding a conflict-free solution by progressively refining the agents' paths. On the other hand, RRT* is an extension of the Rapidly-exploring Random Tree (RRT) algorithm, aimed at optimizing paths for single-agent planning in continuous spaces. RRT* builds a tree by randomly sampling points and expanding the tree towards these points. It enhances path quality through a process called rewiring, where the newly added nodes are used to potentially shorten existing paths. This incremental optimization allows RRT* to converge to an asymptotically optimal path, making it suitable for scenarios where high-quality paths are required [8]. While CBS excels in managing multiple agents and avoiding collisions, RRT* is valued for its ability to refine paths and improve their quality over time. After seeing the pros of CBS and RRT*, it is easy to assume putting it together is a great idea, and that is exactly what we propose is this paper.

1.3. How it works

In the beginning each agent plans a path on its own using RRT*. To achieve this, the RRT* algorithm is used to help each agent identify an ideal route that spans its origin and destination locations without running into any obstacles.

Once the initial paths are planned, CBS look for conflicts between these paths. It results in a conflict if two or more of these agents are programmed to inhabit the same position (most often all-in) at some time, or if their paths get too close for comfort. If CBS finds a conflict, it handles this by adding constraints. The involved constraints require the affected agents to re-plan their trajectories using RRT* such that they do not yield within the conflict configurations.

Final Path: Paths that are free from conflict where each agent can navigate from its start state to the goal states while navigating through other agents. CBS (Conflict-Based Search) makes sure that the last paths are conflict-free and optimizes them using an RRT* path planner;

1.4. Pseudo Code

Initialize:

Start node q_start

Goal node q_goal

Create a tree `T' with 'q_start' as the root which is empty

While q_goal has not been reached:

a. Generate randomly node q_rand in the search space

b. Search within T for the node which is closest to q_rand, called it as q_nearest

c. Construct a new node q_new by moving in the direction towards q_rand starting at q_nearest, with a range Δq

d. Proceed and logic: If and only if the node q_new there are no obstacles, the node q_new is added to the tree T and the node is connected q_nearest to q_new: T.

e. If there is a distance δ e that compares the two initial newly created corners q_new and q_goal and if v is the distance adopted:

- Then put the goal q_goal into the tree T and cut off the running of the algorithm.

If q_goal has now been attained:

A path to q_goal from << q_start will be traced backwards by looking at the parent of each node.

Return the path

2. Result

Time taken (seconds) for path planning using different algorithms

In the simulations, different arrangements of obstacles is set to see the difference between RRT* and A* in different surroundings.

Test 1.

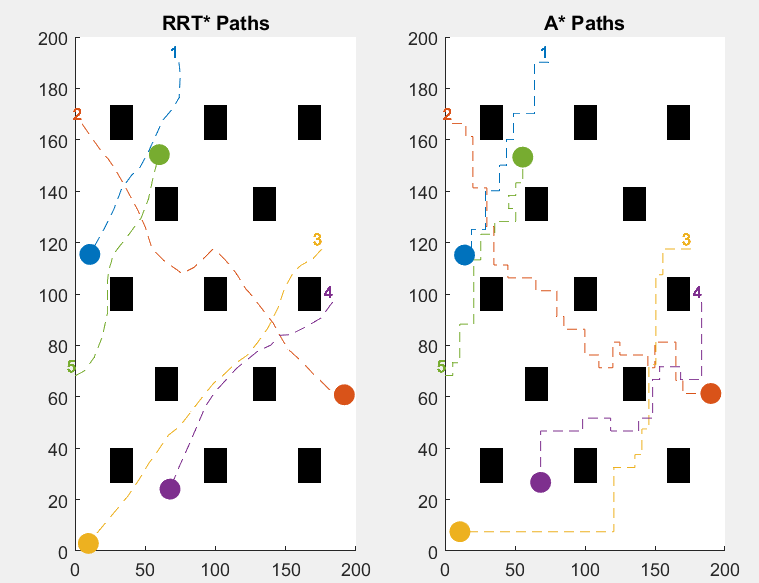
Figure 1. Pathfinding uses CBS with A* (right), and Pathfinding uses CBS with RRT* (left)

Table 1. Time spent by pathfinding using A* and CBS (below), and Time spent by Pathfinding using CBS with RRT* (above)

In the first simulation, all the obstacles are evenly distributed in the entire plain. And RRT* constantly outperforms the A* with their travel times. The travel time for RRT ranged from 21 seconds to 46 seconds while the travel time for A* ranged from 27 to 66. This suggests that in a complex situation, RRT* is more efficient than A* in navigation with multi agent path planning.

Test 2.

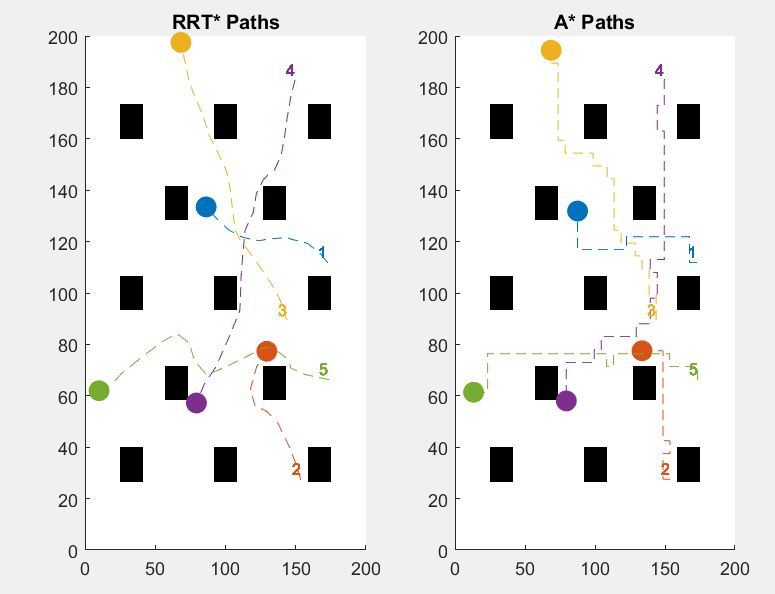
Figure 2. Pathfinding uses CBS with A* (right), and Pathfinding uses CBS with RRT* (left)

Table 2. Time spent by pathfinding using A* and CBS (below), and Time spent by Pathfinding using CBS with RRT* (above)

For the second simulation with the same terrain as the first one, RRT* once again outperformed A* by a lot. Especially shown in the first 3 agents. The time for the agents using RRT* to get to their destination ranged from 14 seconds to 36 seconds, while the time for the agents using A* to get to their destination ranged from 16 seconds to 43 seconds. Once again RRT* is faster than A* showing that the first graph isn’t a coincidence.

Test 3.

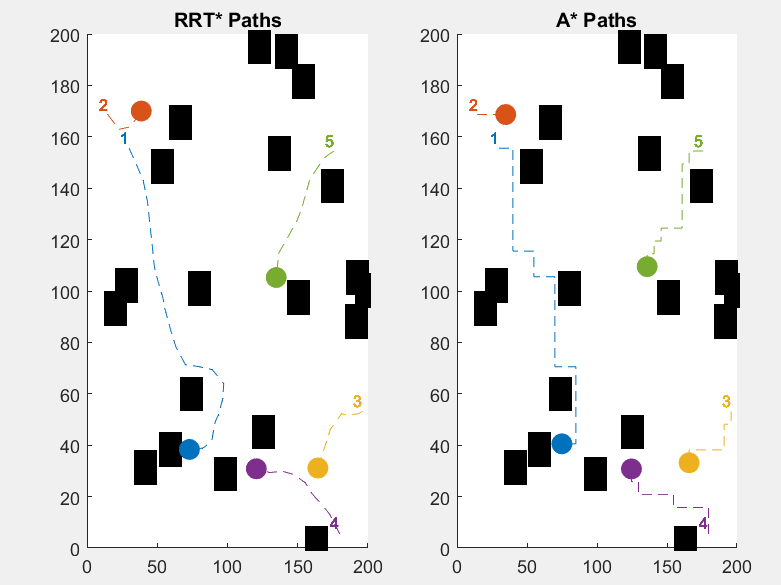
Figure 3. Pathfinding uses CBS with A* (right), and Pathfinding uses CBS with RRT* (left)

Table 3. Time spent by pathfinding using A* and CBS (below), and Time spent by Pathfinding using CBS with RRT* (above)

In the third simulation, the plain has lots of obstacles and they are high noisily located from each othe. In this case RRT* travel times are slightly faster overall—from 6 to 33 seconds. A* this time out competed RRT*in some cases, their time range is from 4-36. This is because since the obstacles are clustered it is likely that there is a straight forward path that A* can take which is often faster than the route RRT* provided.

Test 4.

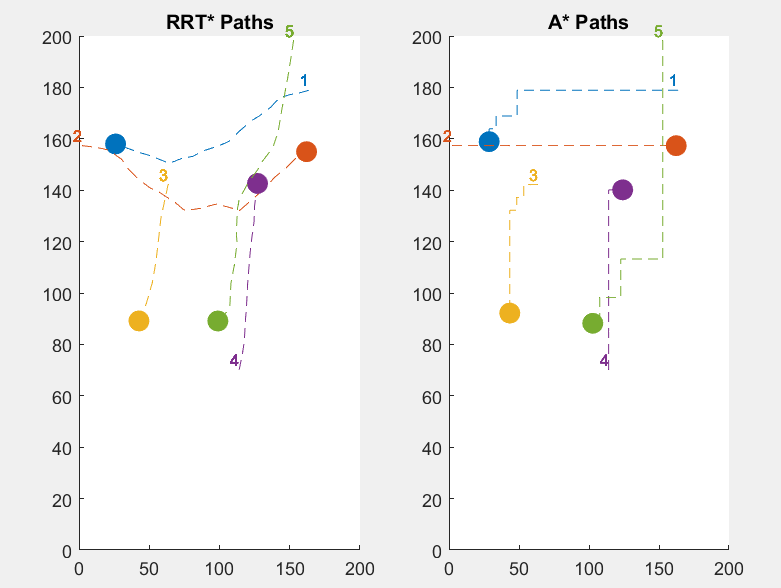
Figure 4. Pathfinding uses CBS with A* (right), and Pathfinding uses CBS with RRT* (left)

Table 4. Time spent by pathfinding using A* and CBS (below), and Time spent by Pathfinding using CBS with RRT* (above)

The fourth simulation is different. It uses a plain with no obstacles. Which is why some agent where able to arrive to their destination using RRT* and others using A*. This is because it is easy for A* to just find a straight path that requires a turn their being fast. However, if RRT* finds a straight path from start to end, it will still be faster than A*. This is shown in the result, the travel times for RRT* ranges from 15 to 34 seconds, while the travel time for A* ranges from 14 to 32 seconds, which indicate that both algorithms perform similarly when the path is clear, with RRT* still maintaining a slight advantage.

Test 5.

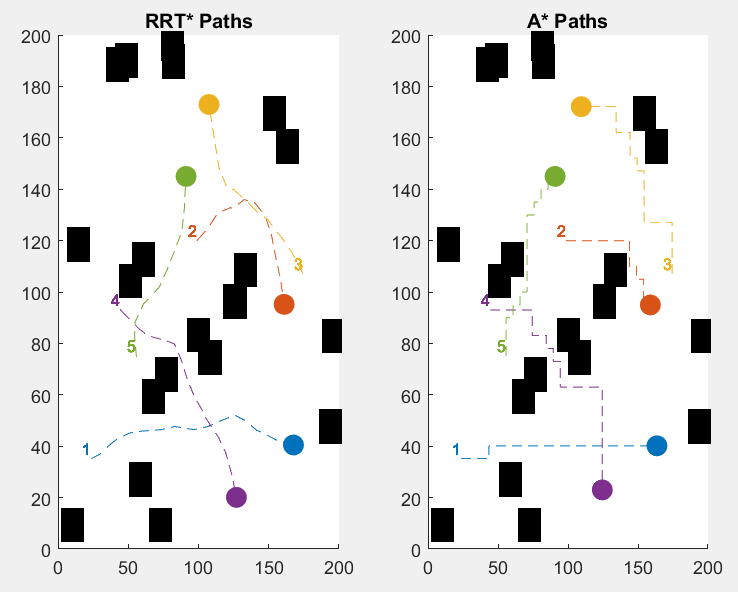
Figure 5. Pathfinding uses CBS with A* (right), and Pathfinding uses CBS with RRT* (left)

Table 5. Time spent by pathfinding using A* and CBS (below), and Time spent by Pathfinding using CBS with RRT* (above)

In the final test, which also have groups of obstacles clustered all together. Both algorithms show similar results, tut this time it is similar because the start and end are closer than most other simulations so it is easy for A* to just find one straight line to the end. But RRT* is still slightly faster when compared with A*. RRT* times range from 16 to 30 seconds, and A* times from 17 to 30 seconds. This shows that even when the situation is easier for A* RRT* still can be faster.

As shown in Figures 1 to 5, the warehouse robots utilize different algorithms for the same starting and ending points. The results are shown in Table 1; the warehouse robot mostly takes less time when the CBS with RRT* algorithm is applied. The main feature of the RRT* algorithm is the ability to find an initial path quickly and then, as the number of sampling points increases, optimize until the target point is found or a set maximum number of cycles is reached. The RT* algorithm is asymptotically optimized; as the number of iterations increases, the resulting path is more and more optimized, and the optimal path can never be derived in a finite amount of time.

3. Discussion

In the research of this thesis (CBS and RRT* combined algorithm) the optimal path algorithm for warehouse robots facing complex environments was solved. However, in the operation of the algorithm the following problem arises: the algorithm is not able to plan the path in continuous time, this problem makes the algorithm slow in the operation of the computation and not able to move the warehouse robot effectively at the same time. So, the algorithm will be optimized in the future so that the warehouse robot algorithm can solve the optimal path planning problem in the face of different robots with different speeds by reducing the discrete nature of the paths and increasing the time factor in continuous time.

4. Conclusion

With the increased demand for shopping by young people, the use of warehouse robots has become important in the efficient management of warehouses. Although there are many robot path algorithms in the society nowadays, many warehouse robot algorithms have many shortcomings to cope with the problem of complex obstacles. In this paper, we propose an improved robot navigation and multi-robot collision avoidance algorithm that combines the RRT* algorithm and the CBS algorithm. This algorithm eliminates the large amount of multi-obstacle processing in the A * algorithm compared to the A * algorithm, so that the robot can move in more directions, based on the CBS algorithm, thus effectively shortening the path planned by the robot. By testing the CBS and RRT* algorithms together several times in complex environments, this study found that the combination of the CBS and RRT* algorithms had a significant impact on complex obstacle problem solving in warehouses. It is expected that this algorithm will be utilized in today's productive society. Future research on warehouse robotics algorithms will focus on increasing the time factor into the algorithm, focusing on increasing the time efficiency of warehouse robot path planning. Additionally, these studies are currently based on computer simulations and more field experiments will be needed in the future to further refine them.

Acknowledgement

All the authors contributed equally to this work and should be considered as co-first author