1. Introduction

Image enhancement refers to the process of applying specific techniques to improve the visual quality of images or highlight certain features, making them more suitable for human observation, machine analysis, or specific application requirements. Therefore, image enhancement technology has an important use in daily life as well as in scientific applications, involving fields including medicine, agriculture, industry and other aspects, especially in medical imaging and scientific research image enhancement research is increasingly concerned. In these fields where the accuracy of details and the signal-to-noise ratio are high, the edges and lines often contain rich information and represent the characteristics of the image, and the enhancement of image edges can better highlight the effective information of the image.

Image enhancement processing techniques have a wide range, which mainly include contrast enhancement, sharpening, denoising, color enhancement and so on according to functional classification. Among them, contrast enhancement is mainly to adjust the grayscale and improve the contrast through histogram equalization [1], and sharpening is mainly to highlight the image edges through operators, i.e., edge enhancement. Denoising is mainly through spatial filtering to improve the signal-to-noise ratio of the image, and color enhancement includes gamma correction [2] and color spatial changes, which can mainly improve the saturation and brightness of the image; the above can be broadly categorized as spatial domain enhancement and frequency domain enhancement.

In the field of image processing, noise removal is a crucial step for improving image quality and enhancing the accuracy of feature extraction and subsequent analysis. Common types of noise, such as salt-and-pepper noise and Gaussian noise, can significantly degrade both the visual quality and analytical effectiveness of images, making efficient and targeted filtering methods essential. Among these, median filtering and Gaussian filtering are classical denoising algorithms that are widely used in practical applications [3, 4]. Median filtering excels at removing discrete pretzel noise due to its median-based robustness [5]. at the same time, it has a good ability to protect the edge of the image, which can be applied to industrial inspection, medical imaging and sensor image pre-processing [6]. Gaussian filtering, on the other hand, is based on the optimization of statistical distributions and the weight convolution of Gaussian distributions, which can effectively smooth Gaussian and random noises, and at the same time has good computational efficiency, and is widely used in the pre-processing stage of target detection, image segmentation and deep learning [7].

Edge enhancement is also one of the core tasks in image enhancement, which plays a crucial role in applications such as target segmentation, feature extraction and object recognition. Among many edge detection methods, Sobel and Laplace operators are two classical and widely used algorithms. Based on the mathematical properties of derivatives, these two algorithms are theoretically robust and reliable in edge detection and enhancement. Sobel algorithm is an edge detection method based on first-order derivatives, which can provide the strength and direction information of edges by calculating the gradient of the image in the horizontal and vertical directions, and it is especially suitable for the edge detection task with directional features [8]. The Laplace algorithm, on the other hand, is based on second-order derivatives and localizes edges by detecting acceleration changes in pixel intensities. It is capable of global edge enhancement but the nature of its second order derivatives makes it more sensitive to noise [9]. Although both Sobel and Laplace operators provide effective tools for edge detection, there are significant differences between the two in terms of the directionality of edge enhancement, response to noise, and applicable image types. Therefore, comparing the results of these two operators and their performance in practical applications can not only help to deeply understand their principles and properties, but also provide practical guidance for the selection and optimization of edge detection algorithms.

This article primarily focuses on the ability to capture detailed information in images and their practical applications. It provides a comparative study of classical algorithms for image denoising and edge enhancement, aiming to evaluate their performance and effectiveness in preserving image quality and highlighting important features for various applications. For image denoising, median filter and Gaussian filter are mainly chosen for comparison. In order to better understand the advantages and disadvantages of median filtering and Gaussian filtering for denoising tasks, and to provide a clear basis for selecting the appropriate image processing method for different types of noise, this paper conducts a comparative study of the effectiveness and applicable scenarios of both filters. By thoroughly analyzing the differences in their results, it has the potential to promote further optimization of subsequent denoising algorithms. In addition, for edge enhancement, this article will systematically explore the processing effect of Sobel and Laplace algorithms and their applicable scenarios, focusing on analyzing their practical application value in image segmentation, feature extraction and edge analysis, and providing theoretical support for the subsequent research and application.

2. Comparison of median filtering and Gaussian filtering for denoising

2.1. Principle of median filtering

The median filter works roughly as follows: first a filter window is defined (usually a rectangular area of 3x3, 5x5 or 7x7), which is moved over the image. The size of the window affects the filtering effect; the larger the window, the smoother the filtered image will be, but at the same time, more details will be lost. For each pixel in the image, the median filter takes the pixel as the center, removes all the pixel values within the window (including the center pixel and its surrounding pixel values), and arranges the extracted pixel values in order from smallest to largest. Then it selects the middle value, called median, from the sorted values. For a 3x3 window with 9-pixel values, it will sort and select the 5th value as the median. Finally the median filter replaces the original center pixel value with the median value. This process is repeated for each pixel in the image until the entire image has been processed.

2.2. Median Filter Processing and Characteristics of the Processed Image

The algorithmic implementation of the image median filter in Matlab is based on the above principle. First of all, using the principle of median filter and mathematical expression, define a median filter function mid_filter. then the input image is converted to grayscale photo output as the original image, with the definition of a good median filter function mid_filter processing of the original image, the output of the processed image. The median filter before and after processing is shown in Figure 1.

Figure 1: Original and Median filter processed plots

In order to make the contrast of the filtering effect more obvious, this paper chooses the original image with obvious noise as the processing object. As can be seen in Figure 1(a), there are a large number of black and white pixel dots and textured noise in the image, which are in strong contrast with the original image and seriously affect the human eye perception. One of these black and white noises is what we call pepper noise (salt is white dots, pepper is black dots), while the texture-like noise is likely to be high-frequency noise or gradient noise, which may originate from sensor noise, artifacts of texture data, electromagnetic interference, and other aspects in practical applications. These noises interfere with the detailed information of the image and cause breaks and discontinuities in the edge features.

While in Figure 1(b) it can be seen that the overall visual quality of the image is improved after median filtering. First of all, the pepper noise is greatly reduced. For example, the white noise on the dark side of the building, which contrasts strongly with the background, is almost completely eliminated after median filtering, and this satisfactory filtering result is closely related to the characteristic of median filtering that replaces the extreme pixel values by the median value of the window. Secondly, due to the nonlinear filtering feature of median filtering, the edge characteristics are well preserved in the processed image, and it can be observed that the contours of the building, the straight line features and the structural details are still clear after the filtering, and they are not blurred by the denoising. Even at the transition between the light and dark sides of the building in the lower right corner, the layers and edge details that were originally covered by the noise are presented, and the detail features are clearer. In addition the random texture-like noise in the processed image is also reduced compared to the original image, but the smoothing effect is limited, and there is still a large amount of high-frequency noise present.

2.3. Principle of gaussian filtering

Gaussian filter is a linear smoothing filter, the core of the idea lies in the convolution operation of an image using Gaussian function. Its main function is to reduce the noise in an image by smoothing while preserving the overall structural properties of the image.

The general principle is that a sliding window (Gaussian kernel) is shifted point by point across the image, weighting the neighborhood of each pixel with an average [10]. Then the weighted sum of the intensity values of all the pixels in the neighborhood and the corresponding Gaussian kernel value is used as the output pixel value, which determines the denoised image.

2.4. Gaussian filtering process and characteristics of the processed image

The algorithm is implemented in Matlab to apply median filtering to images. With sigma value set to 2 and the Gaussian kernel size left at its default setting, the results before and after Gaussian filtering are shown in Figure 2.

Figure 2: Original and Gaussian filter processed plots

The figure before processing was selected from the same original image as the median filter processing (Figure 2a), and there is obvious granular and textured noise in the figure, with broken and jagged edge lines. After Gaussian processing, as shown in Figure 2(b), the most significant change is the enhancement of the overall smoothness of the image. And it can be seen that both the gray scale and the luminance in the processed image become more continuous and the transition is more natural. For high-frequency textured noise, it is significantly weakened after Gaussian filtering, and the image looks softer and more uniform, and the background area becomes cleaner. For pretzel noise, it is also smoothed after Gaussian filtering, but it can be seen that the pretzel noise is not really removed, but only “spreads” to the surrounding pixels to form a blurred tiny bright spot.

Although the outline of the building remains intact in the Gaussian filtered image, the sharpness of the straight edges of the building is slightly reduced due to the blurring of the edges by the Gaussian filter itself, which shows a slight blurring. Gaussian filtering also weakens the high-frequency details present on the surface of the building in the process of smoothing the high-frequency noise, such as some texture structure features. In addition, the overall contrast of the image is slightly reduced due to the Gaussian filtering which weakens the extremes of the bright and dark points of the image, which on the one hand reduces the interference of the extreme brightness contrast in the image, while on the other hand it reduces the overall visual impact of the image.

2.5. Comparison of the two filters in practical applications

By comparing the denoising results of median filter and Gaussian filter on the same image, different denoising advantages and applicable scenarios can be found. As a nonlinear filter, the median filter can deal with pretzel noise (discrete noise) in a more targeted way, but it has limited smoothing effect on Gaussian noise, and it has to sort each pixel neighborhood, which has high computational complexity and may increase the computational cost when dealing with high-resolution or large-scale images. Therefore, in dealing with continuous noise and large-scale real-time image processing, Gaussian filtering is more advantageous, which is used as a linear smoothing filtering method to reduce the noise intensity by smoothing operation. However, Gaussian filtering also has a blurring effect on the edge details, which may lead to feature loss, thus based on the results of this filtering, it can be found that the median filtering is more capable of achieving a good balance between edge preservation and noise removal in scenes with high detail requirements.

In practical applications, the use of these two methods is often determined according to different noise types, image characteristics, and task requirements. For example, remote sensing images are often interfered by various noises in the acquisition process, including sensor noise, atmospheric interference, and pretzel noise. Median filtering performs well in removing scatter noise from remote sensing images. For example, in UAV aerial photography and monitoring, median filtering can retain the boundary characteristics of features while removing noise, thus improving the accuracy of information acquisition. Moreover, the median filter can better preserve the texture of the building appearance and improve the clarity. On the other hand, Gaussian filtering can also be applied in remote sensing image processing, it is more suitable for smoothing the wide range of background noise, especially in high-resolution remote sensing images, it can reduce the interference of high-frequency texture and sensor noise, and at the same time, Gaussian filtering is more suitable for dealing with the uneven background illumination of the remote sensing image to improve the overall image quality. However, for edge monitoring and other aspects, Gaussian filtering is rarely used in remote sensing.

In addition, noise removal in medical images (e.g., CT, MRI, and ultrasound images) plays a critical role in enhancing diagnostic accuracy and facilitating subsequent analysis. Median filtering has demonstrated outstanding performance in medical image processing. For example, in CT images, it effectively eliminates discrete noise caused by data transmission or hardware malfunctions while preserving critical edge and detail information, such as organ contours and lesion areas. In contrast, Gaussian filtering is often employed in medical imaging to smooth background noise, particularly in cases of Gaussian noise, such as random noise in MRI images. However, its potential to blur edges warrants careful consideration. Therefore, for medical imaging, the choice of an appropriate filtering method should be based on the specific noise type, and in some cases, a combination of both techniques may yield optimal results.

3. Comparison of Sobel and Laplace operators for edge enhancement

3.1. Principles of the Sobel and Laplace operators

Sobel operator highlights the edge features in horizontal and vertical directions by computing the gradient transform of the image pixel values [11]. To achieve this, the pixel values of the image need to be extracted first and then the pixel values its convolution operation to detect the edges in different directions.

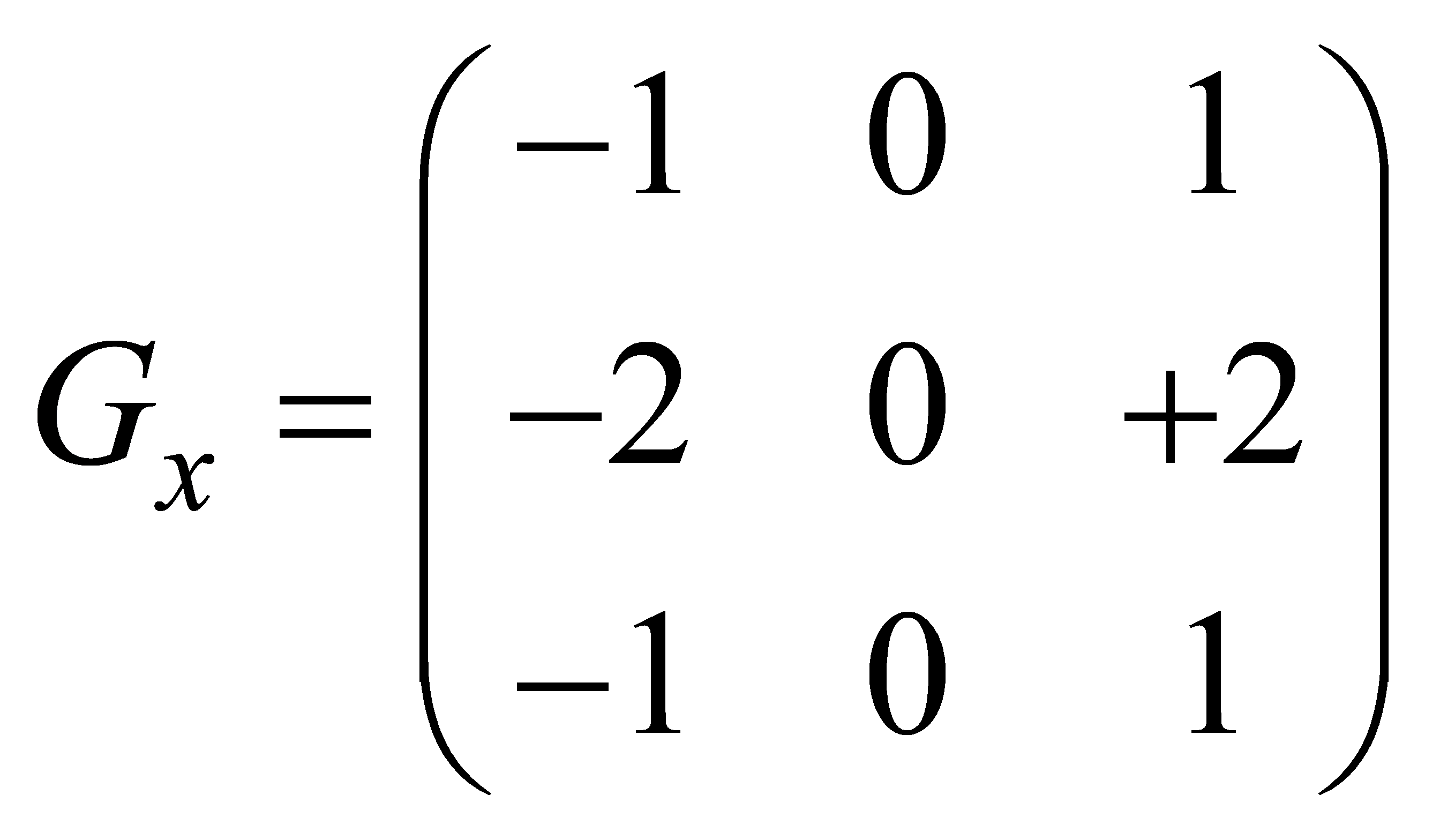(1)

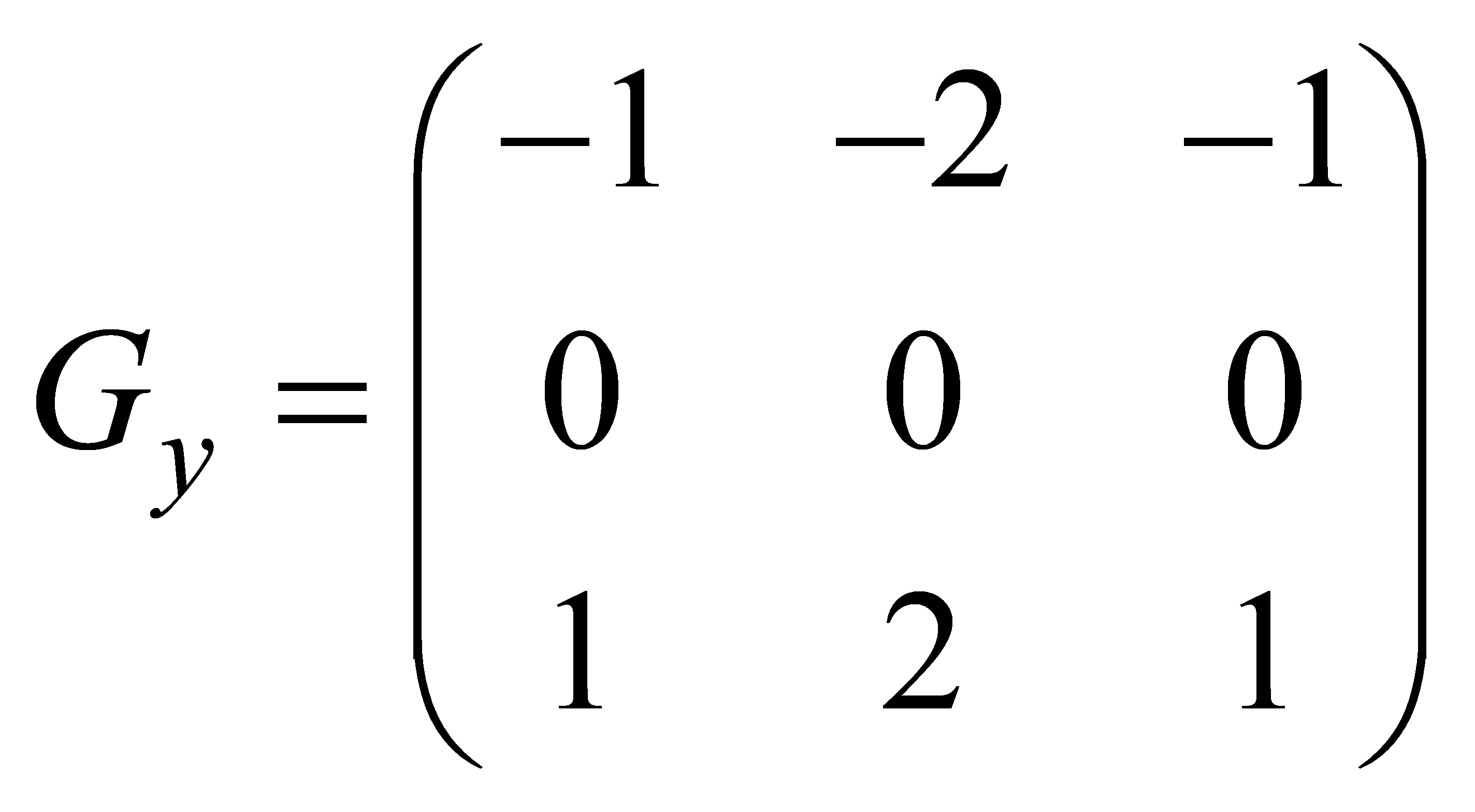(2)

The rate of change of pixel values in both directions is obtained by convolving the image using these two convolution kernels separately.

(3)

Finally, the edge information obtained from the Sobel operator is superimposed on the original pixel values to realize edge enhancement.

Laplace operator detects the edges by second order derivatives and superimposes them to the original image to realize the image enhancement. Firstly the second order derivatives of the image are calculated using Laplace operator and the Laplace operator selected in the implementation of the algorithm in this paper is as follows.

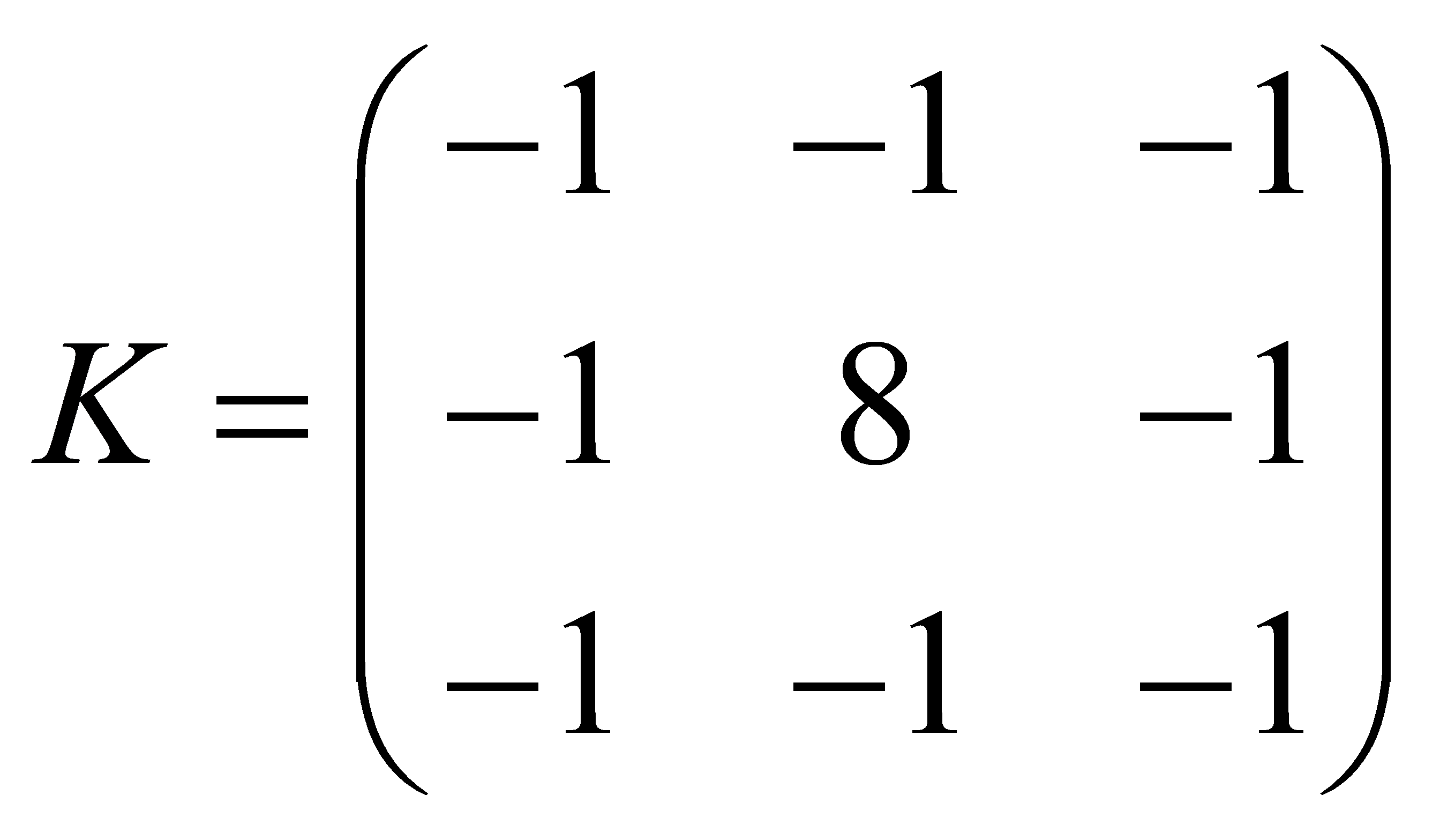(4)

This operator takes into account the second order rate of change in the horizontal, vertical and diagonal directions simultaneously. The second order derivatives of each pixel can be calculated by convolution with the operator, and finally the sharpened image is obtained by simply taking the absolute value of the result of the Laplacian operation and adding it to the original image prime value.

3.2. Sobel operator implementation and processed image properties

When using Sobel's algorithm for color image enhancement, a channel-by-channel approach is adopted to effectively preserve the color information of the image while emphasizing the edge features. Specifically, I(:, :, c) is used to extract the pixel values of the R, G, and B channels of the color image. Then, imgradientxy is used to calculates the horizontal (Gx) and vertical (Gy) gradients for each channel. Finally, image enhancement is performed according to the operator's principles.

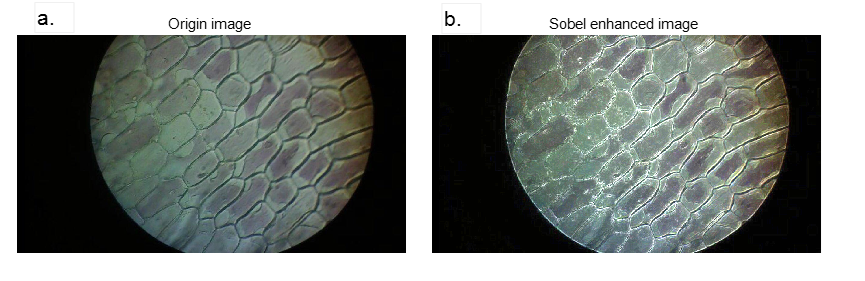
Figure 3: Origin image and Sobel enhanced image

The image before processing in Figure 3a is an unenhanced original color image, which presents a natural state overall, with a soft and delicate background, low contrast between the cell boundary and the background, and blurred and insufficiently prominent outlines. This kind of image is suitable for overall observation, but it is difficult to meet the requirements for tasks that require clear segmentation of boundaries or extraction of details (e.g., cell identification or morphology analysis). After processing with Sobel's algorithm, the result of directional edge detection, when superimposed with the original pixel values, approaches the maximum, causing the pixels to display very bright colors. This significantly enhances the edge features in the image, making the cell boundaries clearer and the brightness contrast strongly with the background. Meanwhile, as can be seen from Figure 3b, the smoothing characteristics of the background region are weakened, making the visual focus more concentrated on the edge part. The image enhanced with the sobel operator is suitable for tasks that require recognition and segmentation of targets, such as cell outline detection and feature extraction under the microscope. This processing significantly improves the boundary clarity and provides higher utility and accuracy for subsequent morphological analysis and automatic segmentation.

3.3. Laplace operator implementation and processed image properties

Similar to the processing of Sobel operator, Laplace operator also processes the pixel values of R, G, and B channels and adds them to the original pixel values, and finally outputs the enhanced color image.

Figure 4: Origin image and Laplace enhanced image

As shown in Figure 4, before processing, the texture information in the image is more uniform, but the edge characteristics are relatively weakened. The overall contrast of the image is low, making it difficult to accurately capture edge details. This makes the image suitable for observing the overall structure, but not effective for highlighting local detailed features. At the same time, the high-frequency information of the image is similarly highlighted, and both the intracellular details and the boundary changes become more delicate. The Laplace operator makes the edges in the image more conspicuous by enhancing the regions with large intensity variations, while the homogeneous regions are suppressed. However, in Figure 4b, we can also see that there is an increase in the granularity of the cell edges and internal details, which is caused by the noise-sensitive nature of the Laplace operator. The Laplace operator may amplify the noise in the image, and therefore is often used in conjunction with Gaussian smoothing filtering and other processes [12]. Globally, the Laplace operator works better than the Sobel operator in more detail processing, which enhances the boundary information of the whole image and provides a stronger edge contrast effect for subsequent cell segmentation and feature extraction.

Figure 5: Images before and after jointly processed by Sobel and Laplace operators

By comparing the images before and after processing in Figure 5, it can be found that the joint processing realizes the superposition of the processing effects of the two operators. It can be observed that the edges and internal details of the cells in all directions are very clear, and the brightness of the edges is significantly improved and strongly contrasted with the background.

3.4. Comparison of the two operators in practical applications of image enhancement

The combination of both the Sobel and Laplace operators enhances the edges and details of an image, making it sharper. This sharpening effect is very useful in image preprocessing and image enhancement, such as in medical imaging and satellite image analysis to better identify and observe details.

The Sobel algorithm calculates the gradient through the first-order derivatives, which is good at enhancing directional edges, retaining details better, and is more effective in processing noisy images, and is suitable for tasks that require clear edge direction, such as surveillance video and road boundary recognition, etc. The Laplace algorithm is based on the second-order derivatives, and is able to globally enhance multi-directional edges, and can sharpen the boundaries and lines of any direction, which makes it suitable for medical images. This isotropic feature makes it suitable for organ boundary extraction in medical images and other aspects, but it is sensitive to noise and usually needs to be combined with smoothing filter.

Sobel operator considers both horizontal and vertical gradients and has a smoothing effect, so it is more effective in processing images with more gray scale gradients and noise, while Laplace operator is more sensitive to singularities or boundary points, and the combination of the two can improve the accuracy of edge detection. In automated and robotic vision systems, accurate edge detection is critical for object recognition and navigation. In the vision system of self-driving cars, the Sobel operator may be used in order to detect road edges and traffic signs quickly and accurately; while at the same time, the advantage of the Laplace operator in multi-directional edge processing makes it more accurate for road detection and traffic sign recognition, etc. Although Laplace operator is more sensitive to noise, by using it in combination with Sobel operator, the effect of noise can be suppressed to a certain extent, especially when image sharpening is performed.

In surveillance video analysis, the Sobel operator may be chosen to ensure processing speed and noise immunity. However, Sobel operator is not very accurate for edge localization, and Laplace does have a greater advantage in providing more accurate edge locations. Therefore, in scenes where accurate edge localization is required, one may consider using the Laplace operator first or a combination of the two operators. For example, using the Sobel operator for directional edge enhancement before using the Laplace operator for accurate edge localization can help to improve noise immunity and stable target detection in complex lighting and dynamic scenes.

In practical applications, the operators can be selected according to the specific content of the image and the processing goals. In scenarios that require more edge information, such as medical imaging, the Laplace operator may be more appropriate; while in surveillance videos, due to more noise, it may be necessary to rely more on the Sobel operator.

4. Conclusion

This paper systematically explores the different effects and application scenarios of classical denoising and edge enhancement algorithms in the field of image enhancement, and through a comparative study of two denoising methods, median filtering and Gaussian filtering, this paper summarizes the advantages and limitations of each. Median filtering is excellent in dealing with pretzel noise and edge detail retention, and is more suitable for scenes that need to retain texture features, while Gaussian filtering is more suitable for smoothing Gaussian noise and a wide range of background areas. The experimental results show that a reasonable choice of filtering method can significantly improve the image quality when the noise type and processing goal are clear.

In terms of edge enhancement, this paper compares the characteristics and applications of Sobel operator and Laplace operator. The experimental results show that the Sobel operator is good at extracting directional edge information and is suitable for dynamic scenes and tasks with high demand for noise immunity. While the Laplace operator realizes high sensitivity to details through global enhancement and is suitable for application scenarios with precise boundary localization. The combination of the two operators demonstrates stronger edge detection and detail preservation capabilities in complex image processing, providing effective support for medical image analysis, remote sensing image processing and machine vision tasks.

The research in this paper provides theoretical basis and practical reference for the application optimization of image enhancement technology. And it provides a reference for the selection of algorithms in practical applications through an in-depth discussion of the performance of classical algorithms and applicable scenarios｡

Future research can focus on adaptive denoising algorithms, deep learning combined with traditional methods and further optimization of real-time image processing. Meanwhile, multi-scale and multimodal image processing techniques can be developed to adapt to the image enhancement needs of different resolutions and modalities (e.g., infrared images, radar images, etc.). Especially considering the diversity of image noise and the complexity of processing needs, exploring smarter and more efficient algorithms will further enhance the application potential of image enhancement. In addition, with the advancement of hardware technology, the combination of FPGAs and other hardware platforms can further enhance the efficiency of image processing and provide technical support for emerging fields as well as cross-domain applications such as medical imaging and environmental monitoring.