1. Introduction
Within the Digital Signal Processing (DSP) architecture, power consumption has always been a crucial aspect when it comes to designing; one common approach to achieve this is through approximation, which lowers power usage at the expense of reduced calculation precision. Nevertheless, within a variety of error-resilient applications including multimedia and image/video processing, where error tolerance is relatively high, approximation designs can be especially suitable for such purpose. Since adders, multipliers, and compressors are some of the most imperative components in the DSP, a variety of these approximate components have been introduced in different DSP architectural designs and applications for the sake of reducing power consumption. There are many schemes on the optimization of approximation designs, generally at the algorithm level, architecture level, and circuit level; these schemes have been summarized in~[1]:
- At the algorithm level, logarithm-based, linearization-based, and hybrid approximations are proposed.
- Within the architecture level, a range of approximation strategies are introduced and conversed upon at different stages of a conventional exact multiplier. These include truncating input operands or partial products, modifying partial products, employing approximate compressors during the accumulation phase, and strategically placing these approximate compressors in the accumulation process.
- From a circuit level, techniques of approximation are able to be implemented following the previously discussed methods at the architecture and algorithm levels. Specifically, these include Boolean rewriting, gate-level pruning, evolutionary circuit design, and Voltage Over-scaling (VOS).
This paper will include the design of approximate compressors at the architecture level and Boolean rewriting and VOS technique at circuit level; this paper will mainly focus on the gate-level optimization of approximate compressors and transistor-level modification of mirror adder (MA), which respectively corresponds to the component of compressors and adder in multiplier. This paper analyzes proposed designs from three studies and aspects: The first section explores the design and use of approximate adders to optimize power consumption in digital signal processing (DSP) discussed in~[2]. Approximate adders are designed with fewer transistors and simpler logic operations compared to conventional exact adders, resulting in reduced power usage. This reduction in power consumption is achieved at the cost of introducing some tolerable computational errors. The referred study ~[2] specifically demonstrates this design approach through the modification of mirror adders and evaluates their performance in applications such as video and image compression. By analyzing power and error models, various formulas and charts derived from the models to compare the performance of different approximation variations in adder circuits, which helps underscore both the advantages and drawbacks of employing approximate adders in low-power DSP applications. The second section analyzes two approximate 4:2 compressors utilized in multipliers that are discussed in~[1]. Such a kind of design is based on a trade-off between imprecision in computation (error rate i.e. NED) and circuit-based figures of merit (number of transistors, delay, and power consumption). Four distinct schemes for a Dadda multiplier are proposed and analyzed. Comprehensive simulation results are included, and the application of these approximate multipliers in image processing is demonstrated. The result demonstrates that two of the proposed multiplier designs are seen to deliver brilliant performance for image processing based multiplication in respect to the error metrics and power consumption. Overall, the study demonstrates that the approximate compressors for multiplication utilized in DSP have a huge potential in optimizing power consumption, especially in multimedia and image processing applications which have a relatively high tolerance in computation accuracy. The third section demonstrates dual-quality 4:2 compressors with exact and approximate modes discussed in~[3]. This section is organized into four main parts: the first part describes four proposed 4:2 compressors by providing the circuits and structures. The second part analyzes the precision in processing of Dadda multipliers using these compressors. The third part compares the compressors' design parameters in exact and approximate modes. The last part demonstrates the performance of the proposed compressors in image processing applications. Finally, the study concludes that most compressors offer great trade-offs between accuracy and power consumption.
2. Background
2.1. MA architecture
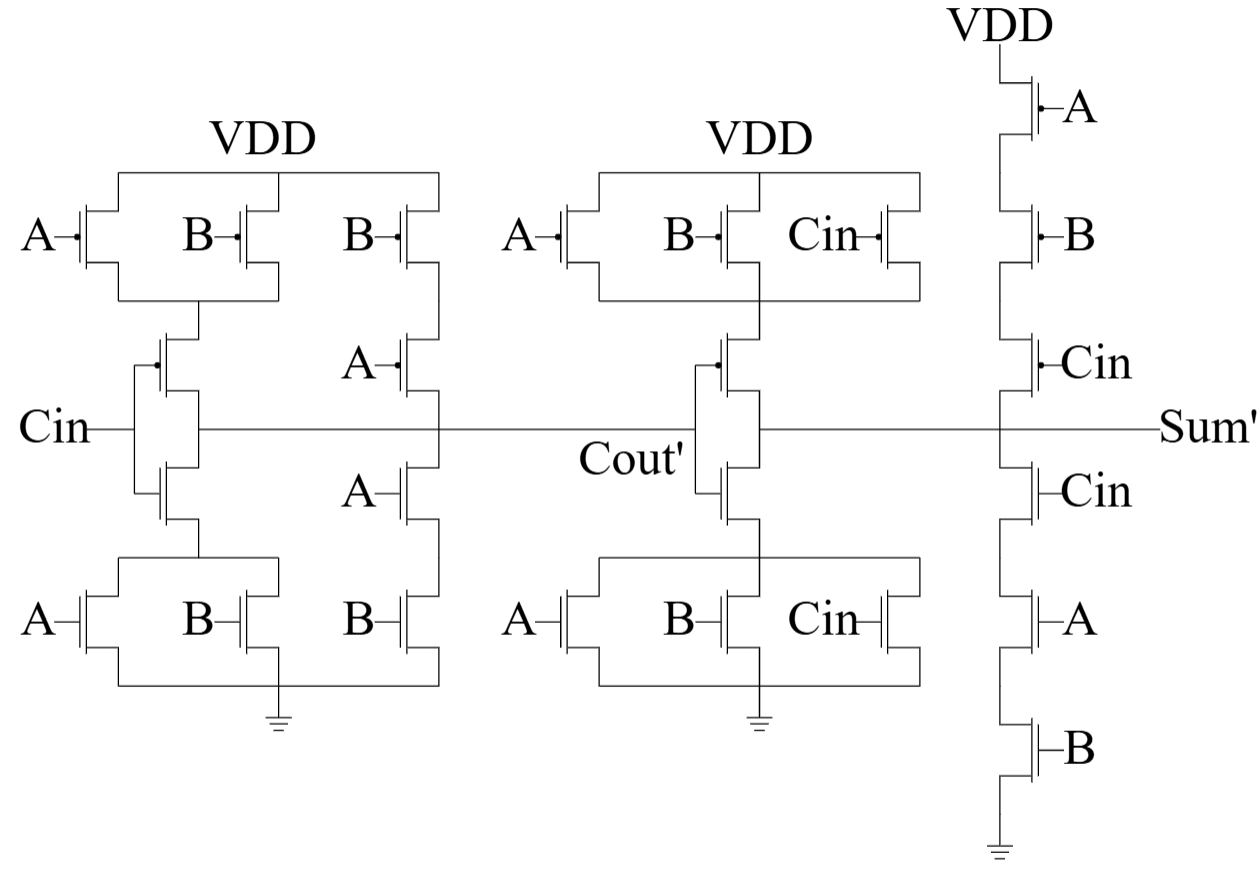
The~[2] study is based on the approximation of mirror adders. Mirror adders refer to a class of architectures in adders where the adder consists of a symmetrical structure as shown in Fig.3 for parallel computations, essentially reducing the propagation delay and some power consumption with a reduced length of the critical path as well as a smaller area of circuit.
2.2. Multiplication and usage of the 4:2 compressors in multiplication

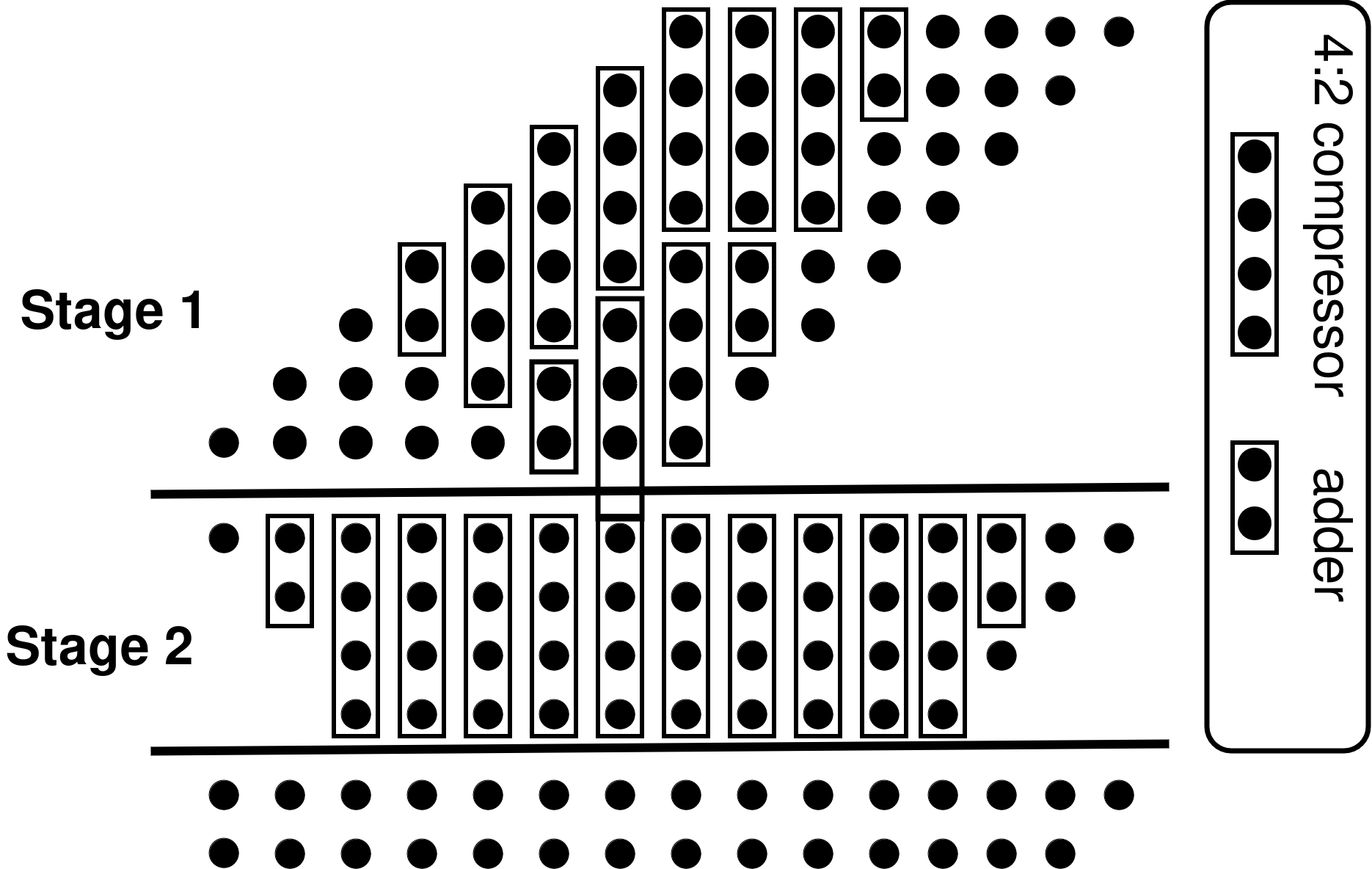
Considering the nature of digital 1,0, the multiplication can be divided to addition and shifting. For example, as shown in Fig.~1, \(y_{0}\) multiplies with each bit of the multiplicand x ({ \(x_{0}\) , \(x_{1}\) , \(x_{2}\) , \(x_{3}\) }), then a partial product for the first row ({ \(p_{3,0}\) , \(p_{2,0}\) , \(p_{1,0}\) , \(p_{0,0}\) }) will be generated. Afterward, this process is repeated for the other bits of the multiplier y ( \(y_{1}\) , \(y_{2}\) , \(y_{3}\) ) and finally 4 rows of partial products are generated (the black dot represents for a bit of a partial product). Because a single bit of a partial product can be created using an AND gate, it can be generated without the need for a carry. Once all the partial products are generated, we can utilize an array of adders to accumulate the partial products. In order to accelerate the accumulation of the partial products and decrease the power dissipation of circuitry, some tree-based reduction circuits had been proposed, such as the Wallace tree and the Dadda tree. Compressors are implemented to accelerate the accumulation process by compressing partial products, counting the number of ones within a group. To enhance compression efficiency, higher-order compressors, such as the 4:2 compressor, have been introduced, as illustrated in Fig.~2.

3. Low-Power DSP: Approximate Adders~[2]
3.1. Approximate designs
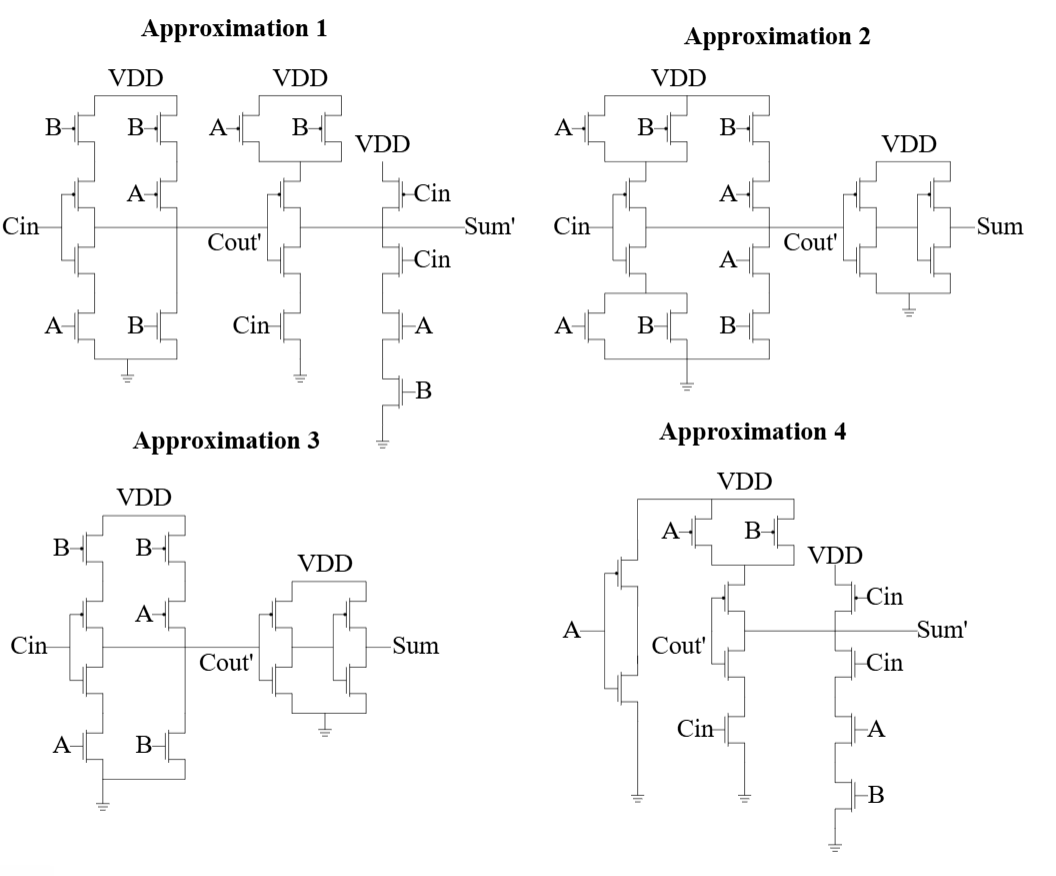
As the structures of conventional DSP systems greatly rely on addition and multiplication operations, this makes them especially power consuming during the computational process. In this section we discuss the design and implementations of approximate adders to optimize power consumption in DSP applications proposed in ~[2]. The study in ~[2] proposes the use of approximate adders as a solution, which reduce the complexity and power usage of arithmetic operations through modifications of the adder’s transistor level architecture at the cost of introducing minor, tolerable errors. However, this approximation is dedicated to being used for calculations of the least significant bit (LSB) within a computational process as for assurance of overall quality. Specifically, the referred study ~[2] focuses on the mirror adder (MA) and how to simplify the logic within the adder by reducing the number of transistors required for computation to reduce power consumption. The referred study ~[2] displays and discusses different methodologies of designs between five approximations of the MA in Fig.~4, where each approximation includes a different number of transistors in the design/logic to compare the approximations from various aspects of logic transistor level complexity, accuracy of calculations, and power consumption.
\begin{table*}[t] \caption{Truth table of Approximations 1 to 4, displaying the precision of the approximated adders compared to the conventional adders from Fig.4 and Fig.3}
| Inputs | Accurate Outputs | Approximate Outputs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(A\) | \(B\) | \(\overline{C_{\mathrm{in}}}\) | Sum | \(C_{out}\) | Sum | \(C_{out 1}\) | \(\mathrm{Sum}_2\) | \(C_{out2}\) | \(\mathrm{Sum}_3\) | \(C_{out3}\) | \(\mathrm{Sum}_4\) | \(C_{out4}\) |
| 0 | 0 | 0 | 0 | 0 | \(0 \checkmark\) | \(0 \checkmark\) | \(1 \times\) | \(0 \checkmark\) | \(1 \times\) | \(0 \checkmark\) | \(0 \checkmark\) | \(0 \checkmark\) |
| 0 | 0 | 1 | 1 | 0 | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) |
| 0 | 1 | 0 | 1 | 0 | \(0 \times\) | \(1 \times\) | \(1 \checkmark\) | \(0 \checkmark\) | \(0 \times\) | \(1 \times\) | \(0 \times\) | \(0 \checkmark\) |
| 0 | 1 | 1 | 0 | 1 | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(1 \times\) | \(0 \times\) |
| 1 | 0 | 0 | 1 | 0 | \(0 \times\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(0 \times\) | \(1 \times\) |
| 1 | 0 | 1 | 0 | 1 | \(0 \checkmark\) | \(1 \checkmark\) | \(0\checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) |
| 1 | 1 | 0 | 0 | 1 | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) | \(0 \checkmark\) | \(1 \checkmark\) |
| 1 | 1 | 1 | 1 | 1 | \(1 \checkmark\) | \(1 \checkmark\) | \(0 \times\) | \(1 \checkmark\) | \(0 \times\) | \(1 \checkmark\) | \(1 \checkmark\) | \(1 \checkmark\) |
\end{table*} The study~[2] introduced the different variations of approximations by intricately removing the transistors from the overall circuit of the conventional MA. As the conventional MA consists of 24 transistors, the objective of the design is to remove as many transistors as possible while maintaining a balanced error rate. The core to this design method is in how to remove transistors from the circuit within the adder as there is a set of rules to follow instead of mindlessly removing them by an arbitrary fashion:
- Ensure that no input combination of A, B, and \(\mathrm{C_{in\lt /strong\gt }\) leads to short or open circuits in the displayed generalized schematic.} In order for a circuit to work it is required to maintain its basic logic by ensuring that the transistors on the critical path of the circuit remain as part of the adder circuit to perform basic calculations.
- Resulting simplifications are expected to cause only minimal errors within the truth table of the redesigned/experimented FA.
Based on the given truth table from table [???], it demonstrates the errors from each approximation in comparison with the conventional MA. This is a straightforward demonstration of the error to transistor count, allowing engineers to balance the number of transistors and errors for reliability. For example, in Approximation 1, eight transistors were removed from the conventional MA schematic. It resulted in one error in \(\mathrm{C_{out}}\) and two errors in Sum. Meanwhile, 10 transistors were removed in Approximation 2 as it took a different approach in design and sets Sum = \(\mathrm{C_{out}}\) with an added buffer stage where there were only two errors in Sum and no errors in \(\mathrm{C_{out}}\) , resulting in less errors and less transistors compared to Approximation 1. According to the two approximations, the referred study ~[2] was able to reference and design approximations 3 and 4 with different performance based on the previous two approximations. Approximation 5 was then designed by extending approximation 4 by allowing one additional error and offers two choices: Sum = A, \(\mathrm{C_{out}}\) = A and Sum = B, \(\mathrm{C_{out}}\) = A. The second choice, Sum = B, \(\mathrm{C_{out}}\) = A, is preferred for minimizing number of errors as it matches the correct results/outputs in four out of eight cases displayed in table [???] (expressed using tick marks and crosses), and is implemented in the RCA addition of 20-bit integers to reduce carry propagation and save circuitry.
Table 1: Choosing approximation 5: table demonstrating truth table of approximation 5, architecture of approximation 5 is overall similar to approximation 4 but 5 includes two variations where Sum could be equal to A or B which leads to different performance and outputs demonstrated in the table.
Choice 1 Choice 2 Sum \(=A\) \(C_{out}=A\) Sum \(=B\) \(C_{out}=A\) \(0 \checkmark\) \(0 \checkmark\) \(0 \checkmark\) \(0 \checkmark\) \(0 \times\) \(0 \checkmark\) \(0 \times\) \(0 \checkmark\) \(0 \times\) \(0 \checkmark\) \(1 \checkmark\) \(0 \checkmark\) \(0 \checkmark\) \(0 \times\) \(1 \times\) \(0 \times\) \(1 \checkmark\) \(1 \times\) \(0 \times\) \(1 \times\) \(1 \times\) \(1 \checkmark\) \(0 \checkmark\) \(1 \checkmark\) \(1 \times\) \(1 \checkmark\) \(1 \times\) \(1 \checkmark\) \(1 \checkmark\) \(1 \checkmark\) \(1 \checkmark\) \(1 \checkmark\)
3.2. Approximate design: Impact of Transistor Reduction on Power Consumption
The approximation design has reduced the number of transistors and simplified the overall circuit, however, its impacts on power consumption need to be further discussed in order to thoroughly understand the purpose of the design. From a basic understanding of the dynamic power expression, a few improvements on the power consumption of the approximation design can be noticed in the following aspects:
- Power dissipation: Based on the dynamic power dissipation expression \(P_{dynamic}=\alpha C V_{d d}^2 f\) where the higher the capacitance load C, the more dynamic power dissipation the circuit outputs; Each transistor within the circuit works by charging and discharging, requiring a certain amount of capacitance and power consumption for each transistor in an operation. By reducing the number of transistors reduces the switched capacitance ( \(\alpha\) C term), which directly lowers dynamic power dissipation.
- The approximation design in the adder also enables voltage scaling from the following two aspects as to reduce power consumption and improve overall performance:
- Area reduction: fewer transistors mean fewer paths and fewer components, allowing the critical paths of the circuit to be shorter and less complex. The study ~[2] uses a table that demonstrates the area usages of every approximation compared to the conventional adder; the approximated adders demonstrate a significant improvement in area savings.
- Propagation delay: simplification of logic at transistor level reduces the propagation delay through the reduction in gate capacitance. In the conventional MA, the input capacitance \(\mathrm{C_{in}}\) is made up of six gate capacitances (refer to 3). Approximation 1 decreases this number to five gate capacitances. Approximation 4 reduces it further to three gate capacitances, and Approximations 2 and 3 bring it down to just two gate capacitances (refer to 4). This reduction leads to a quicker charging and discharging of the \(\mathrm{C_{out}}\) nodes during carry propagation. ~[2]
However, in order to practically evaluate its capabilities and performance in reducing power consumption as well as calculation precision, the referred study ~[2] utilized derivations of simplified mathematical models for estimating the mean error and power consumption based on the number of transistors removed in their approximation configurations.
3.3. Modelling error calculations
For calculating errors, authors and researchers of this article ~[2] were able derive the mean error calculation based on the error in approximate addition when y least significant bits (LSBs) are approximate, allowing us to better understand the precision of the approximated adders. With these derived calculations, the researchers in the study ~[2] were able to create a graph that compares the performance of the five approximations and truncation based on the average error of approximated addition. As inspected, approximation two has the least amount of mean errors and approximation four had the most amount of errors of the approximations, proving the evaluations from the truth table from table [???] to be correct about reliability in precision of calculations for the approximations.
3.4. Modelling power consumption
With the precision aspect of the approximations evaluated, now we turn to focus on the other core aspect: power consumption. As mentioned previously, the power consumption and dynamic power dissipation of the adder is dependent on the circuit's overall capacitance.
3.4.1. Power Consumption Estimate
By dissecting the transistor schematic provided in figure4, it can be confirmed that the adder circuit is mainly composed of NMOS and PMOS transistors to form the CMOS circuit for the MA, yet the two types of transistors hold slightly different capacitance properties, specifically the gate and drain capacitance, that needs to be taken into consideration. It calculates total capacitance at nodes A, B, and \(\mathrm{C_{in}}\) of the adder using the relationships \(\mathrm{C_{gp} \approx 3C_{gn}}\) and \(\mathrm{C_{dp} \approx 3C_{dn}}\) , with the total capacitance at the node A and B approximated as \(\mathrm{20C_{gn}}\) , and at \(\mathrm{C_{in}}\) as \(\mathrm{16C_{gn}}\) . For an RCA of bit width N with y approximate bits, the total switched capacitance \(\mathrm{C_{sw}}\) is given by: \[\mathrm{( y - 1 )C_{app}+yS_{app}+( N-y )( C_{acc} + S_{acc} )}\] The scaled voltage due to approximation is: \[V_{\mathrm{DDapp}}=V_{\mathrm{DD}}(1-\frac{y p}{T_c})\] where P is derived from the simulations. The power consumption \(\mathrm{P_{app}}\) is then estimated as: \[P_{app}=(1 / 2) C_{s w} V_{DDapp }^2 f_c\] providing a first order approximation dependent on the number of approximated bits y. This mathematical modeling helps estimate the power consumption of approximate adders by considering the capacitance of each node, the number of transistors, and the impact of voltage scaling due to approximation.
3.5. Application and testing proof
According to the previous theories and proofs on the approximate design of the MA, there is enough foundational reasoning attained for further applications and testing of theory. Similar to other approximate design applications, the referred study~[2] puts the design to the test in the form of image and video compression, collecting power consumption and peak signal-to-noise ratio (PSNR) data as a metric to verify the quality of the processed outcome. The study utilized two types of methods of computation, discrete cosine transform (DCT) and finite impulse response (FIR) filter, as to demonstrate the performance of the approximate design in the adder. However, for the sake of understanding, there will only be discussion about its performance for DCT as it contains more data on the PSNR metric. With their experimental data displayed in a table titled "Quality and Power Results for DCT" later in the article ~[2], it can be directly visualize that the quality and power results of the approximations from DCT computations for image and video compression. After comparing the results, it can be concluded that approximation 5 obtains the best overall performance with a maximum power saving percentage of 69.32 while maintaining decent quality of computations. Besides using the DCT image/video compression data as an evaluation of the performance of the approximations, the referred study ~[2] also mentioned a comparison with approximated multipliers. The referred study ~[2] compared approximate multipliers that used Karnaugh map simplification from another study ~[4] with an 8 × 8 multiplier that was built with the approximate FA cells from Fig.4. Power consumption and mean errors were assessed for various approximations and compared to prior data. The results highlight the fact that approximation 4 presents a better performance compared to the partial product's approach when it comes to larger mean errors, and the partial product method reaches its limit more quickly than approximations 4 and 5. The power consumption was determined by conducting comprehensive Nanosim simulations for both precise and approximate 8 × 8 multipliers. The average errors for these cases were then calculated using MATLAB, following the methodology outlined in ~[2]. In this section, we get a deliberate view and understanding of how the approximated design was proven to be theoretically and practically successful in reducing power consumption at the cost of tolerable errors. Nevertheless, the design of approximation is not only applicable in adders, it is also seen in other structures of the DSP system such as compressors and multipliers which we will further discuss with the following two studies/papers.
4. Multiplication: Approximate Compressors~[1]
4.1. two designs of approximate compressor
Several low power designs of compressors (i.e. 4:2 compressor) are mentioned in the study~[1], mainly used to compare with the two designs of approximate compressors to test the power performance and accuracy of the two designs. Those schemes are listed below:
- Replace the precise full adder (FA) cell with an approximate FA cell, such as~[5]..
- Utilize the optimized (exact) 4:2 compressor designs described in [6], [7]
In the study~[1], in order to have better power performance than previous schemes, two designs are presented to decrease rate of error while having a better performance than exact compressors in number of transistors, delay and power consumption.
4.1.1. Design 1
Based on the truth table for the exact compressor, the carry output is equivalent to the \(c_{in\lt /em\gt \) } value in 24 out of 32 states. In Design 1, because of this similar pattern, the carry can be simplified to \(c_{in\lt /em\gt \) }; Although this may cause huge difference for making the other 8 outputs wrong, it is capable of being counterbalanced through the simplification of \(c_{out\lt /em\gt \) } and sum outputs. Specifically, the simplification will first turn the sum value in the second half of the truth table of the exact compressor into zero, reducing the variance between the exact outputs and the approximate ones, as well as the complexity of the design; Then, by modifying the value of \(c_{out\lt /em\gt \) } in certain states, the design will become simpler and the error distance provided by approximate carry and sum will be decreased. The simplified Boolean logic expressions are listed below: ( \(Carry^{'\lt /em\gt \) } represents for the approximate value of Carry)
\[
\(Carry^{'\lt /em\gt \) }=Cin
\]
\[
\(Sum^{'\lt /em\gt \) }=\overline{ \(Cin\) }( \overline{x1 \oplus x2}+ \overline{x3 \oplus x4} )
\]
\[
\(Cout^{'\lt /em\gt \) }=\overline{(\overline{x1x2}+\overline{x3x4})}
\]
Noticeably, these expressions are much simpler than that of the exact compressor, thus its complexity of design as well as the power consumption are significantly decreased. The proposed design has 12 incorrect outputs of 32 outputs (an error rate of 37.5 percent), which is less than the error rate using the approximate full-adder cell of [5].
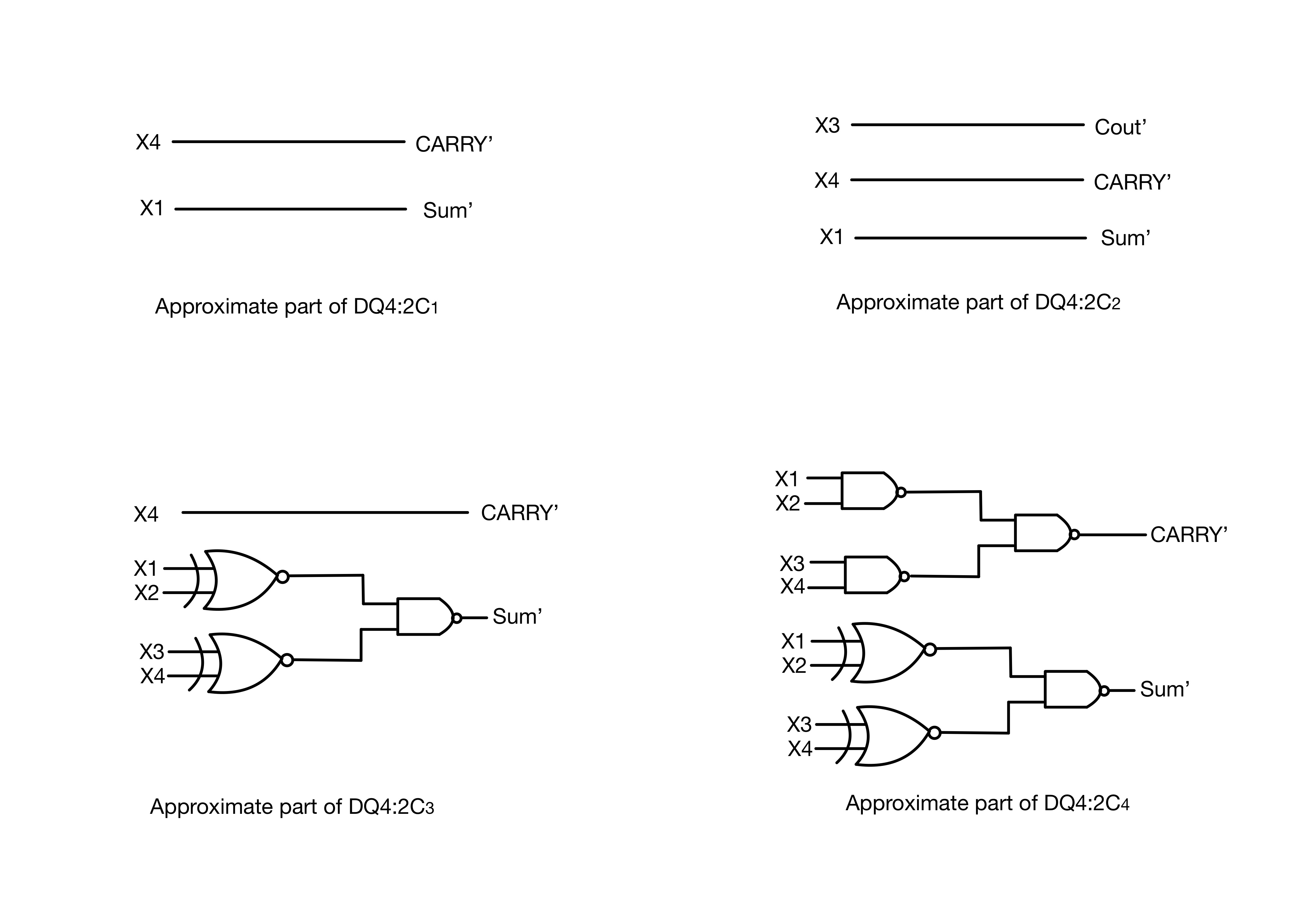
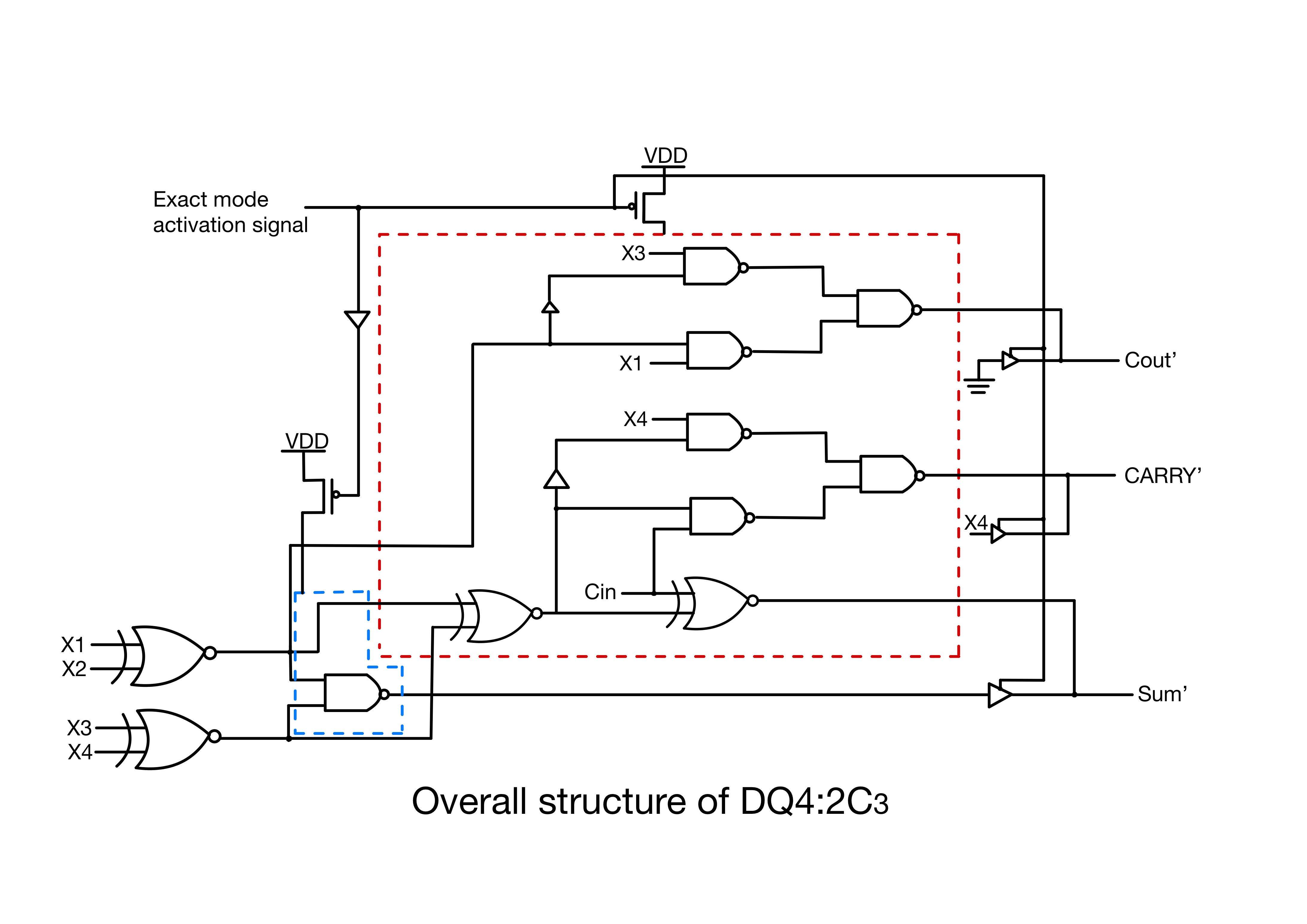
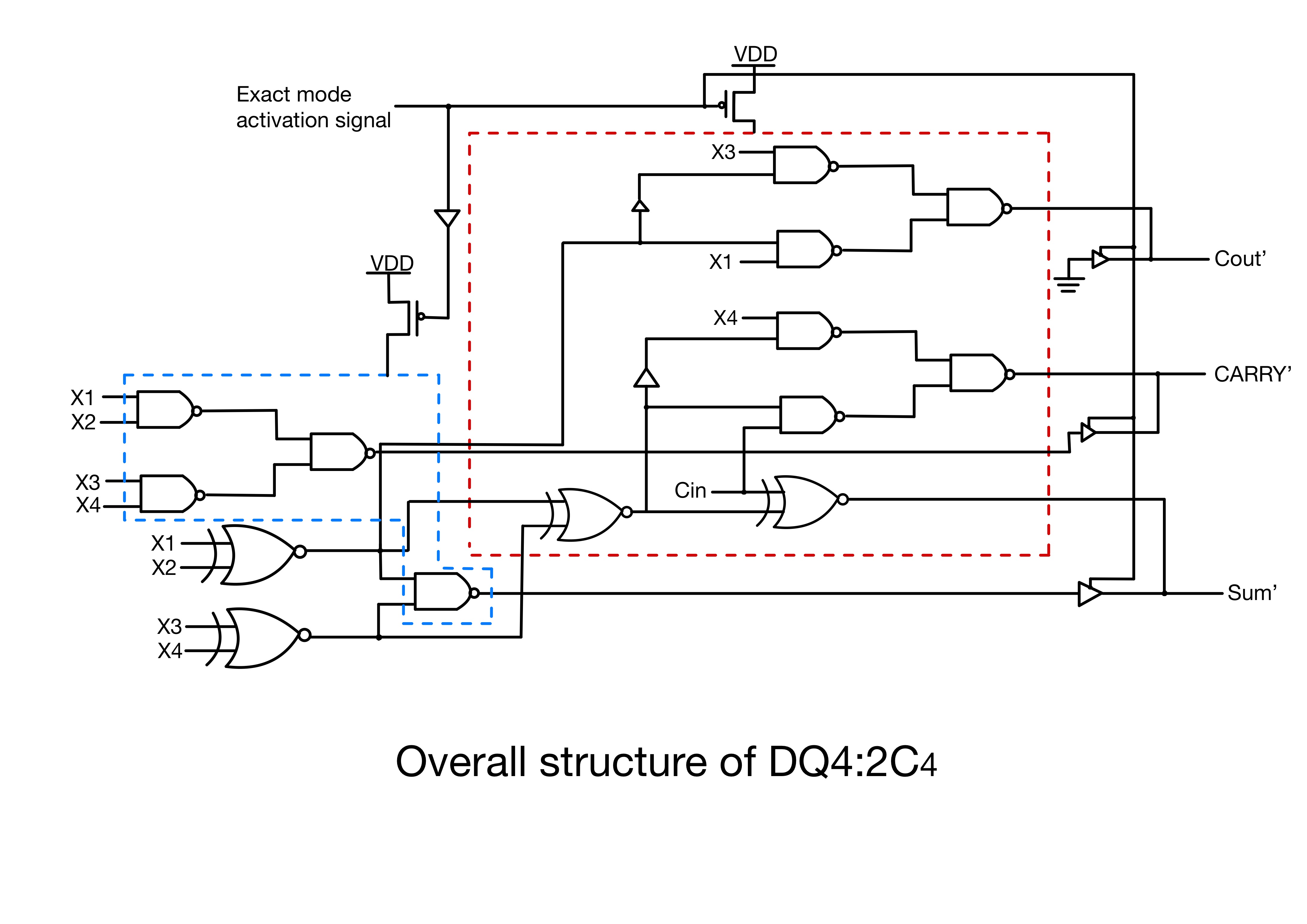
4.1.2. Design 2 4.2. the Implementation of the two Proposed Approximate Compressors for Multiplication 4.3. Simulation Table 2: Simulation results for compressors (PDP:power-delay product) 4.4. Application:image processing 5. Dynamic Accuracy Configurable Multipliers: Dual-Quality 4:2 Compressors~ 5.1. Dual-Quality 4:2 Compressors 5.1.1. Structure 1 (DQ4:2 \(C_1\) ) 5.1.2. Structure 2 (DQ4:2 \(C_2\) ) 5.1.3. Structure 3 (DQ4:2 \(C_3\) ) 5.1.4. Structure 4 (DQ4:2 \(C_4\) ) 5.2. Accuracy Study 5.3. Design Parameters 5.3.1. In Approximate Operating Mode 5.3.2. In Exact Operating Mode 5.3.3. Efficacy Comparison 5.4. Image Processing Application 6. Conclusion Acknowledgment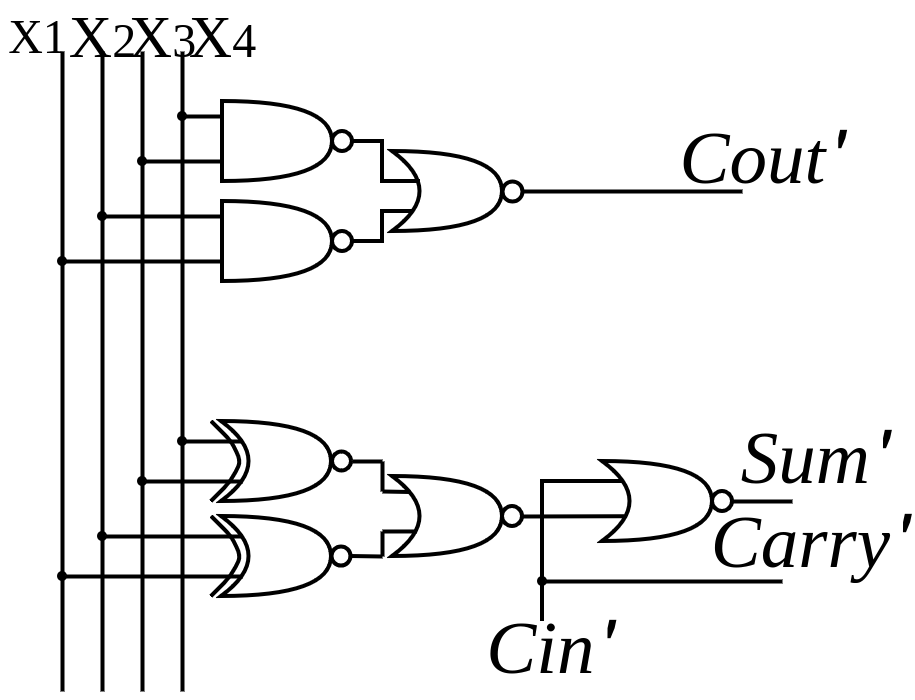
it can be inferred from the results that the design 2 has the optimal power consumption, delay and PDP in those 3 feature sizes. As for delay, power consumption, the 2 designs have significant improvement than the optimized exact compressors.
Design
Delay(ps)
Power( \(\mu\) W)
PDP(aJ)
@32 nm
Exact Design [6]
60.36
2.98
180
Design 1
58.32
1.27
74
Design 2
44.35
1.14
50
@22 nm
Exact Design [6]
55.82
1.50
84
Design 1
56.79
0.62
35
Design 2
41.69
0.58
24
@16 nm
Exact Design [6]
47.59
0.95
45
Design 1
37.16
0.39
14
Design 2
24.44
0.36
9

References
[1]. Amir Momeni, Jie Han, Paolo Montuschi, and Fabrizio Lombardi. Design and analysis of approximate compressors for multiplication. IEEE Transactions on Computers, 64(4):984–994, 2014.
[2]. Vaibhav Gupta, Debabrata Mohapatra, Anand Raghunathan, and Kaushik Roy. Low-power digital signal processing using approximate adders. IEEE transactions on computer-aided design of integrated circuits and systems, 32(1):124–137, 2012.
[3]. Omid Akbari, Mehdi Kamal, Ali Afzali-Kusha, and Massoud Pedram. Dual-quality 4: 2 compressors for utilizing in dynamic accuracy configurable multipliers. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 25(4):1352–1361, 2017.
[4]. Parag Kulkarni, Puneet Gupta, and Milos D Ercegovac. Trading accuracy for power in a multiplierˇ architecture. Journal of Low Power Electronics, 7(4):490–501, 2011.
[5]. Vaibhav Gupta, Debabrata Mohapatra, Sang Phill Park, Anand Raghunathan, and Kaushik Roy. Impact: Imprecise adders for low-power approximate computing. In IEEE/ACM International Symposium on Low Power Electronics and Design, pages 409–414. IEEE, 2011.
[6]. Chip-Hong Chang, Jiangmin Gu, and Mingyan Zhang. Ultra low-voltage low-power cmos 4-2 and 5-2 compressors for fast arithmetic circuits. IEEE Transactions on Circuits and Systems I: Regular Papers, 51(10):1985–1997, 2004.
[7]. Eric J King and Earl E Swartzlander. Data-dependent truncation scheme for parallel multipliers. In Conference record of the thirty-first Asilomar conference on signals, systems and computers (Cat. No. 97CB36136), volume 2, pages 1178–1182. IEEE, 1997.
[8]. Jinghang Liang, Jie Han, and Fabrizio Lombardi. New metrics for the reliability of approximate and probabilistic adders. IEEE Transactions on computers, 62(9):1760–1771, 2012.
[9]. Omid Akbari, Mehdi Kamal, Ali Afzali-Kusha, and Massoud Pedram. Rap-cla: A reconfigurable approximate carry look-ahead adder. IEEE Transactions on Circuits and Systems II: Express Briefs, 65(8):1089–1093, 2016.
Cite this article
Zhong,T.;Shu,S.;Jing,H. (2025). Approximation Design for Low Power Consumption in Digital Signal Processing Architecture: A Literature Review. Applied and Computational Engineering,132,225-240.
Data availability
The datasets used and/or analyzed during the current study will be available from the authors upon reasonable request.
Disclaimer/Publisher's Note
The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of EWA Publishing and/or the editor(s). EWA Publishing and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
About volume
Volume title: Proceedings of the 2nd International Conference on Machine Learning and Automation
© 2024 by the author(s). Licensee EWA Publishing, Oxford, UK. This article is an open access article distributed under the terms and
conditions of the Creative Commons Attribution (CC BY) license. Authors who
publish this series agree to the following terms:
1. Authors retain copyright and grant the series right of first publication with the work simultaneously licensed under a Creative Commons
Attribution License that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this
series.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the series's published
version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgment of its initial
publication in this series.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and
during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See
Open access policy for details).
References
[1]. Amir Momeni, Jie Han, Paolo Montuschi, and Fabrizio Lombardi. Design and analysis of approximate compressors for multiplication. IEEE Transactions on Computers, 64(4):984–994, 2014.
[2]. Vaibhav Gupta, Debabrata Mohapatra, Anand Raghunathan, and Kaushik Roy. Low-power digital signal processing using approximate adders. IEEE transactions on computer-aided design of integrated circuits and systems, 32(1):124–137, 2012.
[3]. Omid Akbari, Mehdi Kamal, Ali Afzali-Kusha, and Massoud Pedram. Dual-quality 4: 2 compressors for utilizing in dynamic accuracy configurable multipliers. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 25(4):1352–1361, 2017.
[4]. Parag Kulkarni, Puneet Gupta, and Milos D Ercegovac. Trading accuracy for power in a multiplierˇ architecture. Journal of Low Power Electronics, 7(4):490–501, 2011.
[5]. Vaibhav Gupta, Debabrata Mohapatra, Sang Phill Park, Anand Raghunathan, and Kaushik Roy. Impact: Imprecise adders for low-power approximate computing. In IEEE/ACM International Symposium on Low Power Electronics and Design, pages 409–414. IEEE, 2011.
[6]. Chip-Hong Chang, Jiangmin Gu, and Mingyan Zhang. Ultra low-voltage low-power cmos 4-2 and 5-2 compressors for fast arithmetic circuits. IEEE Transactions on Circuits and Systems I: Regular Papers, 51(10):1985–1997, 2004.
[7]. Eric J King and Earl E Swartzlander. Data-dependent truncation scheme for parallel multipliers. In Conference record of the thirty-first Asilomar conference on signals, systems and computers (Cat. No. 97CB36136), volume 2, pages 1178–1182. IEEE, 1997.
[8]. Jinghang Liang, Jie Han, and Fabrizio Lombardi. New metrics for the reliability of approximate and probabilistic adders. IEEE Transactions on computers, 62(9):1760–1771, 2012.
[9]. Omid Akbari, Mehdi Kamal, Ali Afzali-Kusha, and Massoud Pedram. Rap-cla: A reconfigurable approximate carry look-ahead adder. IEEE Transactions on Circuits and Systems II: Express Briefs, 65(8):1089–1093, 2016.









