1. Introduction

Multi-objective optimization problem (MOPs) is a problem that requires simultaneous optimization of multiple conflicting objective functions [1]. This kind of problem is widely used in engineering design, supply chain management, resource scheduling, financial investment and other fields. Due to the conflict between the objectives, special optimization algorithms are needed to find a balanced solution.

Traditional single-objective optimization algorithms, such as classical genetic algorithm (GA), although they perform well in single-objective problems, have limited efficiency and quality in multi-objective problems [2]. It usually focuses on searching a certain target, and can not effectively find a balanced solution between multiple targets. However, the solution set of multi-objective optimization problems usually presents Pareto frontier, and the traditional GA has no mechanism to deal with this diversity.

Therefore, researchers proposed multi-objective evolutionary algorithms (MOEAs), among which NSGA-II is a classical multi-objective optimization algorithm [3]. NSGA-II maintains population diversity and finds Pareto optimal solution through non-dominated ordering and congestion calculation. However, with the increase of problem dimension or complexity, the computational cost of GA algorithm will also increase, especially in multi-objective problems with high evaluation cost, and the computational efficiency becomes the bottleneck.

To solve this problem, this paper proposes a strategy that combines intelligent optimization algorithms and machine learning methods to specifically address high and expensive multi-objective optimization problems. In this paper, the combination of random forest and genetic algorithm is selected to implement and verify the algorithm performance for high dimensional problems.

The structure of this paper is as follows: Chapter 1 is the introduction, explaining the research background and motivation; Chapter 2 introduces the basic principles of NSGA-II and random forest, and puts forward the framework of combination. In Chapter 3, experimental results are presented to verify the advantages of random forest in high-dimensional problems, and the performance of different algorithms is compared. Chapter 4 summarizes the research results and looks forward to the future direction.

2. Algorithm principle and combination framework

2.1. NSGA-II Algorithm

NSGA-II (Nondominated Sorting Genetic Algorithm II) is a classical multi-objective evolutionary algorithm, which is widely used to solve multi-objective optimization problems. Its main feature is that it can effectively find the optimal solution set of Pareto while maintaining the diversity of the population, so it becomes one of the important methods in the field of multi-objective optimization. The basic idea of NSGA-II is to classify individuals in a population into different levels according to their domination relationships in the target space through non-domination ordering, and maintain the diversity of the population through the crowding degree distance [4,5,6]. In NSGA-II, individual selection and evolution not only consider individual fitness (objective function value), but also the dominance relationship and crowding degree among individuals, so as to ensure the optimal solution set of Pareto can be found, while avoiding the individuals in the solution set from being concentrated in some areas and ensuring the wide distribution of the solution set.

The main process of NSGA-II algorithm includes the steps of population initialization, selection, crossover, mutation, non-dominated sorting and congestion calculation. The following is the core flow of the NSGA-II algorithm:

-Initialize population: Generate an initial population of randomly created individuals, each representing a potential solution.

-Non-dominated ranking: Rank individuals by dominance, dividing them into Pareto fronts. A dominates B if A is at least as good as B on all objectives and better on at least one.

-Crowding calculation: Calculate the Crowding Distance for each individual in a Pareto front to measure its density in the objective space. Less crowded individuals are more likely to be eliminated.

-Selection operation: Use Tournament Selection to choose parents for reproduction based on non-dominated ranking and crowding distance. Individuals with lower rank or higher crowding are preferred.

-Crossover and mutation: Perform crossover to combine parent individuals and mutation to introduce random changes in decision variables, ensuring global search.

-Merge parents and children: Merge parents and offspring, sort the population by non-dominated ranking and crowding, and select the best N individuals for the next generation.

-Iteration and termination: Repeat the process until a stopping criterion is met (e.g., max generations or optimization goal), and the final solution set approximates the Pareto front.

The advantage of NSGA-II is its ability to preserve multiple Pareto frontier solutions when dealing with complex multi-objective optimization problems, thus providing decision-makers with richer solutions. However, as the size of the problem increases, so does the computational overhead of the algorithm, especially when evaluating a large number of individuals in each generation, and computational time can become a bottleneck.

2.2. Random forest model

Random forest (RF) is an integrated learning method based on decision trees, which can improve the prediction performance and anti-overfitting ability of the model by constructing multiple decision trees [7]. It belongs to the "Bagging" method (Bootstrap Aggregating), which is widely used for classification and regression problems.

The random forest constructs each decision tree through two main strategies:

-Bootstrap Sampling of data sets: The training data is sampled with placement. The data set used for each tree training is a random subset of the original data, usually 2/3 of the data, and the remaining 1/3 of the data is called "Out-of-Bag (OOB)".

-Random selection of features: When constructing each tree, a specific number of feature subsets are randomly selected for splitting at each node, rather than using all features. This process effectively reduces the correlation between trees and enhances the generalization ability of the model.

The construction process of random forest model is as follows:

-Data set sampling: Through Bootstrap method, multiple subsets are randomly selected from the original data set.

-Training decision tree: Train a decision tree on each subset, with each node split using only a randomly selected subset of features.

-Integrated prediction: Each tree makes a prediction, the classification questions vote to determine the final category, and the regression questions use the average to get the final prediction.

Random forest improves accuracy by integrating the prediction results of multiple decision trees, avoiding overfitting problems that are prone to occur in a single decision tree, while maintaining strong prediction ability and low bias. Because of its good generalization ability and strong fault tolerance, it can efficiently process high-dimensional data and give more accurate prediction results.

2.3. Algorithm combination framework

On the basis of NSGA-II algorithm solving steps, the classification model of random forest is introduced in this study. In the calculation process, the classification model is used as an auxiliary judge of fitness function. Specifically, NSGA-II algorithm determines whether a solution is good or bad and whether it is a non-dominated solution through fitness calculation and other operations. After the introduction of classification model, the calculation process can be saved, and the classification model can be used to predict whether the non-dominant solution is directly through the input of individual dimensional values. The children judged as the dominant solution are eliminated directly, and only the individuals judged as the non-dominant solution will be calculated with the fitness function, and the real judgment will be made according to the result after calculation. At the same time, the fault-tolerant mechanism is introduced to ensure the stability of the optimization process, which can greatly reduce the calculation of the real function and reduce the running time of the algorithm while ensuring a certain accuracy. The flow chart of the algorithm framework is shown in Figure 1.

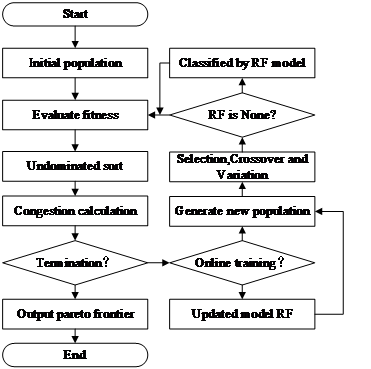
Figure 1: Algorithm flow chart

The algorithm framework can be specifically divided into the following stages:

2.3.1. Data set accumulation stage

In the first 10 generations of the algorithm, the non-dominated solution judgment of all individuals still relies on the traditional NSGA-II method for objective function calculation and non-dominated sorting. The main purpose of this stage is to collect data through traditional genetic algorithms for training random forest classification models. In these 10 generations, the individual's decision variables and their non-dominated solution labels (1 for non-dominated solutions and 0 for dominated solutions) are recorded and gradually accumulated as training set data.

2.3.2. Classification model training and online updating

Starting from the 11th generation, after the initial training of the first 10 generations, the generated random forest classification model will be introduced into the optimization process. In each generation, the classification model predicts whether an individual is a non-dominated solution based on its decision variables:

If the model determines that the individual is the dominant solution (labeled 0), the individual is eliminated directly, skipping the fitness calculation, and reducing the waste of computing resources.

If the model determines that the individual is a non-dominated solution (labeled as 1), the individual continues to enter the traditional fitness calculation and non-dominated sorting stages to ensure the quality of the solution set.

In order to improve the prediction accuracy of the classification model, with the iteration of the algorithm, new training data (that is, new individuals generated by each generation of optimization and their corresponding dominated/non-dominated labels) are continuously added to the training set. The classification model is updated online every 10 generations, and the random forest classification model is retrained with the latest training set, thereby gradually improving the accuracy and generalization ability of the model. Through this online learning mechanism, the classification model can constantly adapt to changes in the optimization process as the algorithm progresses.

2.3.3. Error control and fault tolerance mechanism

In order to deal with the possible errors in the initial stage of the classification model, this paper introduces a fault tolerance mechanism to ensure the stability of the optimization process. When the classification model is uncertain or the prediction error is large (for example, when the prediction probability is close to 50%), the traditional non-dominated sorting algorithm can be used to make the final judgment of the individual to ensure that important individuals are not eliminated due to the classification model error.

With the accumulation of training data and the continuous updating of the model, the accuracy of the classification model will be gradually improved, and the error will be effectively controlled. Therefore, in the later stage of the optimization process, the classification model will play a greater role in speeding up the screening process of non-dominated solutions and further improving the computational efficiency.

3. Experiment and result analysis

In this section, we use high-dimensional multi-objective examples for experiments, first verifying the advantages of RF in various machine learning methods. Then the classical index is used to compare the proposed algorithm with the original NSGA-II algorithm and MOEA/D algorithm.

3.1. Comparison of machine learning methods

To verify the advantages of random forest in multi-objective optimization, we compare it with other common machine learning methods such as support vector machines, k-nearest neighbors, etc. In the experiment, we trained multiple machine learning models and evaluated their performance in predicting the fitness of optimized individuals. The results show that compared with other methods, random forest can provide more accurate prediction in a shorter time, and its generalization ability and stability make it an ideal choice for this study. The experimental results are shown in Figure 2.

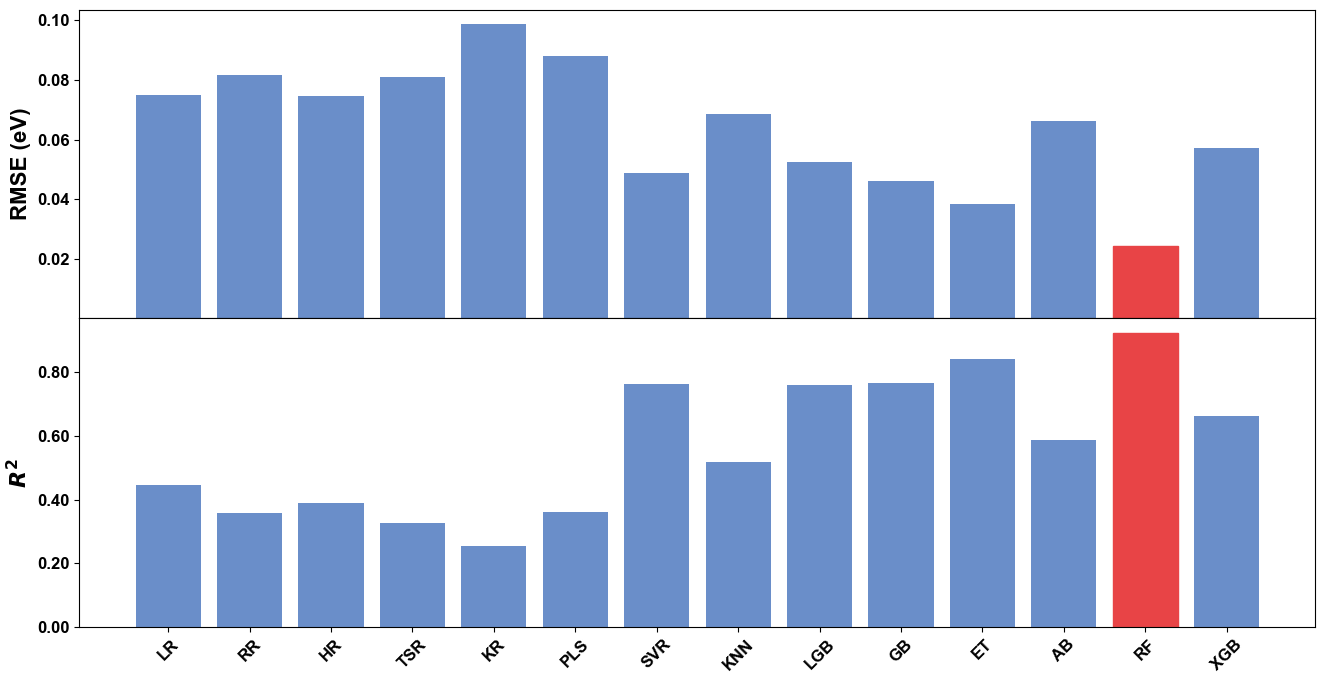
Figure 2: Comparison of machine learning methods

3.2. Algorithm comparison experiment

In the experimental part, the population size of the algorithms in this paper is set at 200 and the number of iterations is set at 500. The running time and IGD values of each algorithm under two high-dimensional problems are recorded and compared. The experimental results are shown in Table 1.

Table 1: Comparison of algorithm running time and indicators

The experimental results show that the proposed method has a significant advantage in computational speed in two high dimensional problems. In problem 1 and problem 2, the running time of NSGA-II algorithm is 53.35% and 61.39%, and the running time of MOEA/D algorithm is 46.67% and 54.36%, respectively. At the same time, although the HV and IGD indexes of the algorithm decreased after the use of RF model, the decrease degree was limited and was within the acceptable range for certain problems. In general, this method is very meaningful in the face of high dimensional and expensive optimization problems that require low precision and quality, but require high computational speed.

4. Conclusion

In this paper, a hybrid optimization method combining genetic algorithm and random forest is proposed, which provides a framework for solving high and expensive multi-objective optimization problems. By introducing the stochastic forest prediction model into the genetic algorithm, we significantly improve the computational efficiency of the optimization process and verify the effectiveness of the method in several experiments.

Although the method presented in this paper performs well in many scenarios, there are still some limitations. For example, in some extremely expensive calculations, the use of classification models alone still does not reduce most of the computation time. Future research could incorporate other machine learning methods or deep learning models and consider replacing some of the real calculations with regression models.