1. Introduction

Path planning is one of the primary components that is considered to be of utmost significance in the field of research pertaining to navigational issues. A route might be thought of as a curve or as a succession of dots that connects a starting point to an ending point, and the technique that creates the path which is required is an essential aspect of path design. The most critical objective of path planning is to locate the least expensive route while avoiding barriers. Oftentimes, a map of the environment, a starting point, an ending point, and, most crucially, a cost function are required to accomplish this objective. Path planning has primarily been solved using classical and heuristic approaches. Classic methods are simple. They usually cost more calculations and fail when face uncertainty comes into the environment. Comprehensive or offline journey planning and local or online journey planning cover all of the approaches to automated journey planning. On the one hand, a high-level path at low resolution is typically generated by a global path planner with a map of the known environment or its perspective information. One of the most critical aspects of research that goes into creating a travel plan is path planning.

Paths are defined as a series of points or curves that extend from a starting place to an ending position, and the process of formulating a path is known as path planning. Paths can be either straight or curved in nature. Local path planning doesn't need prior information about the environment, and a high-resolution low-level path is given by the onboard sensors.

Path planning is widely used in many areas, for example, GPS (Global Position System), urban road planning, autonomous driving and etc. All these show that the exploration of path planning in the future still needs more research to make it more accurate, faster, and more effective. Particularly vital to autonomous driving is navigation, which is just one of its many components. And it is designed to arrive at a target position with path planning, which is one essential component of this process. It decides how the robot is designed to move to the target position and achieve the goal.

In this paper, one of the heuristic methods will be explored, Neural network (N.N.), The future outline of the algorithms of neural networks that can be used to solve path planning is discussed. A neuronal network is a mathematical model of an algorithm that is an imitation of an animal neuronal network and that processes distributed and parallel information. The network processes information by modifying the relationship between a large number of nodes that are connected to each other on the inside. This is done to account for the complexity of the system. The same characteristics of all kinds of N.N. are nonlinear operation, high redundancy, distributed storage, and massively parallel processing. Because of these, N.N. is capable of fast computation speed, strong capacity to form associations, strong ability to adapt, robust fault tolerance, and self-organization. Previous research conducted by Weiwei Jiang and Jiayun Luo has made use of a wide variety of neural graph networks to make predictions about traffic issues. The forecast of the situation of road traffic if it's crowded and speed, the forecast of passenger traffic in the urban rail transport system, and the forecast of demand in car-sharing platforms [1]. N.N. also was used to obtain more precise results by using N.N. to calculate scores with excellent clustering data, which was used as the training set [2]. In the classification of different skin diseases, N.N. was also used to create a machine-learning model [3]. In [4] and [5], neural networks are also incorporated as preprocessors for fuzzy logic controllers, resulting in path-planning improvements for robots.

2. Method

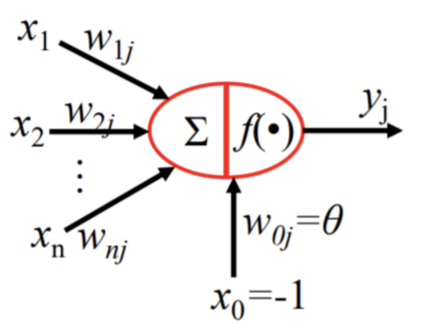
The neural network algorithms mentioned are described in detail here to explain how the neural network was used to solve path-planning problems. A mathematical or computer model that imitates the way in which operations are carried out by a biological neural network is referred to as a neural network. A neural network will be formed by the interconnection of a large number of artificial neurons. As a neural network will often be an adaptive system, changes in its internal structure can be triggered by new information that comes from the outside. Because current neural networks are a statistical nonlinear information modeling tool, they are frequently used to investigate the intricate connections that exist between the inputs and outputs of the system. In 1943, McCulloch and Pitts abstracted the structure as well as the function of neurons in biological neural networks into a simple model, which has been used since then as the "M-P neuron model" [4].

The input signal from other neurons connected to the current neuron is represented by xi(i = 1, 2,..., n) in Figure 1, and the strength or weight of the connection between neuron j and neuron I am represented by wij, The activation threshold of the neuron, also known as the bias, is denoted by the letter I, while the function of activation, also known as the transfer function, is indicated by the letter f. The following equation can be used to represent a neuron's output [1], yi:

\( {y_{i}}=f(\sum _{j=1}^{n}{w_{ij}} {x_{j}}-{θ_{i}}) \) (1)

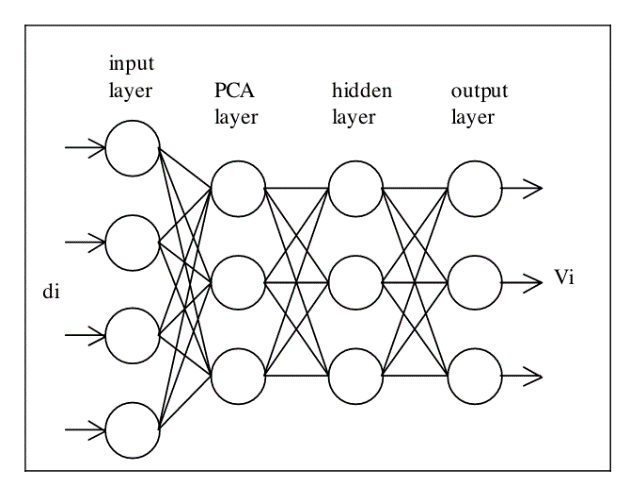
The M-P model is a mathematical simplification of the information processing model of biological neurons, and subsequent research work on neural networks is based on it. Collision-free pathways between obstacles are built using two neural networks according to D.Janglova's solution for path planning for autonomous robots in partially structured settings [6]. The first one employed a principal component analysis network (PCA) to learn the surroundings and solve the traditional find space issue. Unsupervised and supervised learning are combined in one topology via PCA.

The signals from the range finder serve as the input for this neural network, and the free space in the robot's workspace is what the network produces as an output. PCA is a data reduction technique that can both discover uncorrelated features from the input and condense the input data into a small number of primary components. It is also an unsupervised linear process. A compromise between training effectiveness and accurate results will be made in the number of primary components chosen. It is crucial to remember that Hebbian learning can become unstable if the input is not correctly adjusted. Input, output, PCA, and hidden layers are the four layers of the network.

There are two elements to the learning process. A grouping of unrelated features is extracted from the first section's input using an unsupervised linear method, and some of these features will be chosen as main components. The output is provided by the feed-forward supervised parts in the hidden layer. PCA neural networks use Hebbian rules for learning. The learning parameter is updated to a smaller positive number once the synaptic weight wij is initially set to a smaller random number. The changes in yj and weights are then computed for n=1. Equation 2 gives the results

\( {y_{j}}(n)=∑_{i=0}^{p-1} {w_{ij}}(n){x_{i}}(n) \) \( j=0,1,⋯,m-1 \) (2)

Then calculate the weight changes with equation 3 during the learning process by modifying the Hebbian rule.

\( Δ{w_{ji}}(n)=η[{y_{j}}(n){x_{i}}(n)-{y_{j}}(n)∑_{k=0}^{j} {w_{ki}}(n){y_{k}}(n)] \) (3)

\( i=0,1,⋯,p-1 \)

\( j=0,1,⋯,m-1 \)

These estimates of equation 3 will be repeated until the weights finally become stable [8].

A back-propagation technique is used in the second section to implement the network's learning process. The threshold neuron coefficients and synaptic weights are updated in this section. The back-propagation algorithm learns by doing as follows: Data is provided as input, after which the network's response is determined (feed-forward calculation). Equation 4 is used to calculate the amount of deviation that exists between the expected output and the intended output [9].

\( {e_{i}}(n)={d_{i}}(n)-{y_{i}}(n) \) (4)

The di is the intended outcome, whereas the yi is the actual outcome. In the back-propagation process, the local gradient δi of the previous layer is calculated by propagating the error backward. The weights are updated using equation 5.

\( {w_{ij}}(n+1)={w_{ij}}(n)+η{δ_{i}}(n){x_{j}}(n) \) (5)

wij stands for the weight that is carried over from the ith neuron of the preceding layer to the jth neuron of the next layer, and η stands for the rate at which new information is learned. The procedure is repeated in the subsequent input-output pattern as far as the output layer error comes to a predefined threshold or the maximum time of iterations is reached. The mean squared error cost function Avg is given by Equation 6. Equation 6's mean squared error cost function, Avg, is minimized using this method.

\( {E_{avg }}=\frac{1}{N}∑_{n=1}^{N} \frac{1}{2}∑_{j=1}^{V} {({d_{j}}(n)-{y_{j}}(n))^{2}} \) (6)

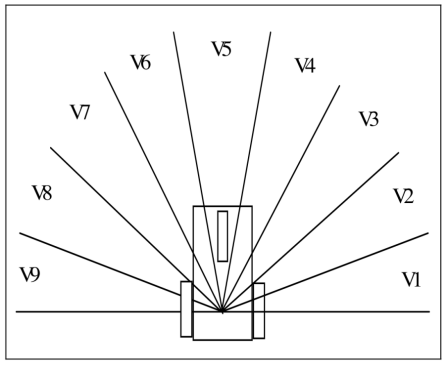
Both the overall number of input-output patterns and the total amount of output neurons are denoted by the notation N and V, respectively. In this situation, the neural network measures each distance of all objects from the robot from 0 degrees to 180 degrees using the standardized data from the ultrasonic rangefinder as input. Then get details about the free segment Vi from the input layer of the network. Every output neuron represents a specific segment of the workspace, as shown in Figure 3.

After solving the find space problem, the next thing has to face is the find path problem.

Also, utilize neural networks to solve this problem; the MLP mentioned above is an example of a hierarchical feed-forward network that was trained using static back-propagation. The key benefit is that it can approximate any input/output mapping and is simple to use. But the disadvantage is that the training is slow and requires a large amount of training data.

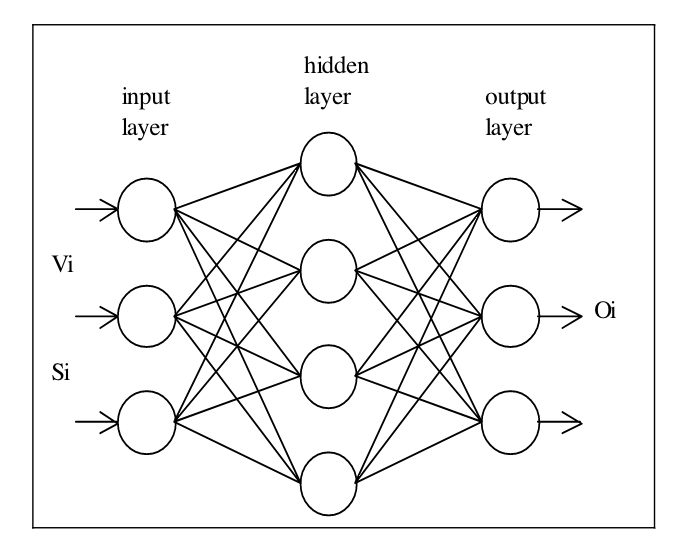
The MLP's function is to use the output of the first network to calculate the azimuth k of the robot's subsequent movement. Figure 4 depicts this network's topology.

Also included in this tiered system are the input, hidden, and output layers. In this instance, the synaptic weights between neurons and thresholds are adjusted. It is analogous to the second stage of learning for the find space issue explained before. The output of the previous neural network, which is the well-known free space segment Vi, is fed into this neural network so that it can process the data. The target segment Si should be located at the robot's target location coordinates. Then get the information about the robot motion direction (azimuth) Oi in that output layer of the MLP neural network. This message is provided to the control unit to complete the movement control of the robot [10].

Subsequently, M.K. Singh et al. did more research based on 44 to determine the free workspace in the robot's working environment [11]. This was done using three robots with different range sensors. From their starting positions, all three mobile robots were able to navigate effectively to their destination. The primary downside of this strategy is the need to collect a large number of training samples (3000 training methods) with varied scenarios. Subsequently, M.K. Singh et al. did more research based on 44 to determine the free workspace in the robot's working environment [11]. This was done using three robots with different range sensors. From their starting positions, all three mobile robots were able to navigate effectively to their destination. The primary downside of this strategy is the need to collect a large number of training samples (3000 training methods) with varied scenarios.

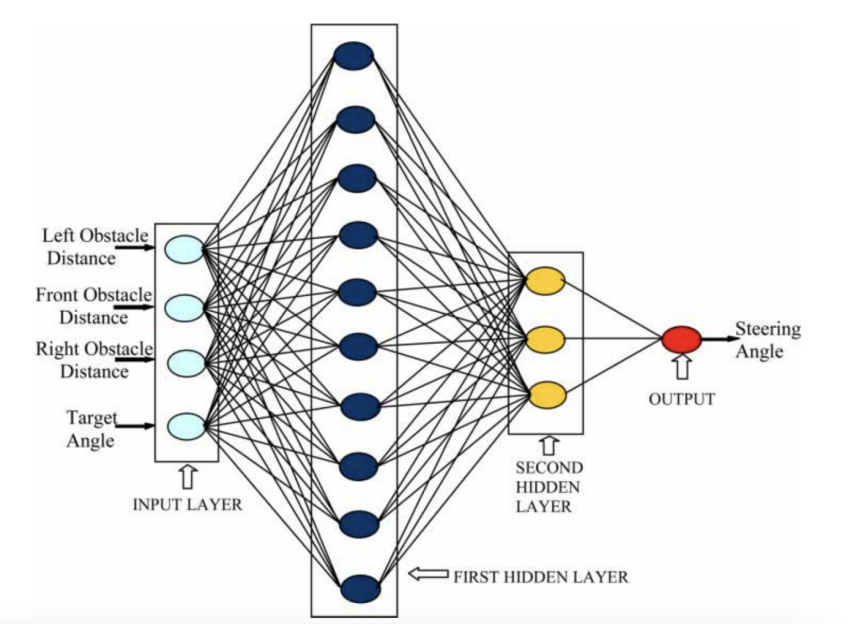
A neural network approach created by M.K. et also allows the robot to traverse safely across uncharted settings that contain both static and moving obstacles [6-8]. The distances between the obstacles in front of, to the left of, and to the right of the vehicle serve as the inputs for this neural network. Figure 5 depicts that its output, like that of D. Janglova's MLP neural network, is the robot's steering angle.

In order to improve the path planning, a four-layer neural network was employed with input from the variety of sensors that were received. Compared to S.H. Dezfoulian and their study, The neural network was educated using just 200 examples of everyday situations [11], significantly reducing the time spent on collecting training samples and computations.

In conclusion, neural networks have already been utilized to develop a broad range of solutions for the path-planning issue faced by autonomous robots, each of which has advantages and drawbacks of its own. Furthermore, the learning algorithm might not ensure that an ideal outcome can be obtained. Therefore, there may need to be a combination of other approaches to perfectly solve the real-world robot navigation problem.

3. Result

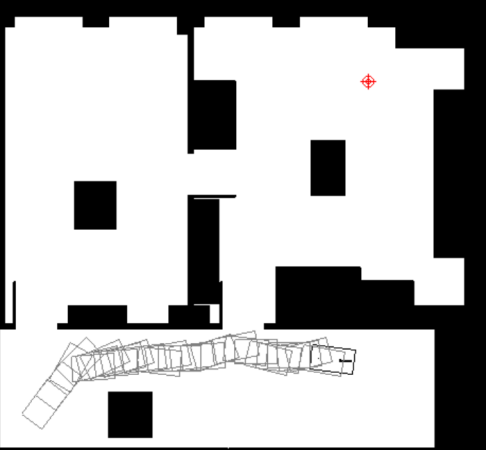
In the study [8], the robot AURO obtained distance images by means of an ultrasonic scanning rangefinder. The swept surface area covers 180 degrees in front of the robot and 20 cm in the vicinity. The speed of rotation and the angle at which the front wheels are turning are what regulate its manipulation. The initial tests were conducted in a learning environment where the robot safely followed each path from a specific beginning point to an endpoint while avoiding any hazards. Subsequently, in the following tests, they were performed in a network learning environment, i.e., an unknown environment. In this environment, the execution paths are also still collision-free. Then use, the algorithm to simulate the motion of the mobile platform, and before adding the neural networks D and H, the robot did not reach the target position (given in figure 6).

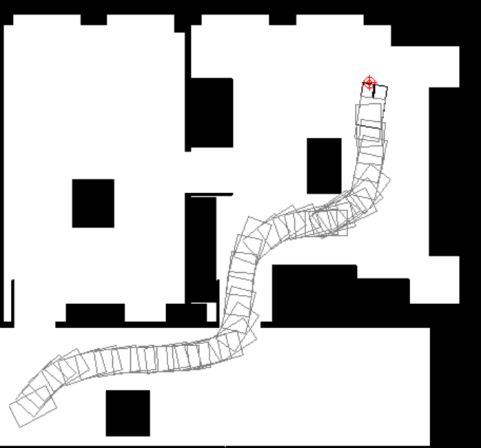
But after adding it, the robot reached the target position, and the whole process was collision-free and safe (given in figure 7).

So the paper [5], proposes that the strategy is appropriate for a robot that needs to move in any environment.

The paper [9], gives performance and cost times for the three distinct extraction techniques, GHA, APEX, and NMF, for training, and obstacle avoidance, besides the ANN series. This information is based on research that can be found in [5]. The values given are averaged over ten performance tests, and the relationships between predictors and response variables are also described in the regression columns. The different feature extraction components with the best performance and training duration are underlined in bold.

The data shown in the table makes it abundantly clear that the NMF's training pace is noticeably and significantly faster than that of the other two methods. When compared to the outcomes of the different techniques, the NMF method yields the poorest results during the training phase. The GHA approach provides the best network training performance and is the most generalizable to the validation set, as can also be observed from the table. Because the APEX method does not perform as well as GHA and takes a longer time to train than GHA, it is not considered to be used.

4. Conclusion

This paper article has a short introduction to the neural network, and then the article show and compares three commonly used neural networks for path planning, navigation, and obstacle avoidance. This paper analyzes the input and output using the fundamental formulations of neural networks in order to comprehend precisely what the inputs and outputs of various neural networks are, as well as how the outcomes influence the realistic movement of autonomous robots. This paper explains precisely how neural networks may handle the path planning problem. Finally, this paper compares and analyzes the results of several neural networks for path planning problems and explains the benefits and drawbacks of each, which can assist us in intuitively selecting an appropriate neural network when utilizing neural networks to solve problems in various situations.

In the future, hoping to introduce new learning methods, such as reinforcement learning and online learning to reduce the workload of neural networks in collecting training samples and to improve the stability of the algorithms in the face of different environments. In the literature introduced in this paper, the sensors used are more common sensors, and in subsequent studies, we also can extend them to different kinds of sensors with varying configurations for robots in natural environments.