1. Introduction

Truss structures have been the backbone of modern industrial architecture for decades, serving as critical components in large-span factories, warehouses, and infrastructure projects like railway bridges. Their triangular geometric configuration creates inherent stability, allowing efficient distribution of both static and dynamic loads. Among various truss designs, the Pratt truss stands out for medium-span applications (typically 12-18 meters), where its parallel chord arrangement and vertical web members provide an optimal balance between material efficiency and structural integrity. This design has become particularly prevalent in Asian industrial parks, where rapid construction timelines and cost-effectiveness are prioritized.

However, the long-term performance of these structures often faces silent threats. Over decades of service, steel members gradually lose their load-bearing capacity due to cyclic stress fatigue—a phenomenon observed in 78% of aging factory buildings according to a 2019 industry survey. Environmental factors accelerate this process: coastal regions face salt-induced corrosion, while northern climates deal with thermal expansion-contraction cycles. The 2021 collapse of a 30-year-old chemical plant roof in Guangdong Province, which caused 17 injuries, tragically demonstrated how hidden axial stiffness degradation (denoted as EA loss) in diagonal web members can lead to catastrophic failures. Zhang et al. 2020[1] incidents underscore the critical need for effective structural health monitoring (SHM).

Traditional SHM approaches have served the engineering community for generations. Vibration-based methods, for instance, detect damage by tracking changes in natural frequencies—a technique successfully applied in the 2015 Sydney Harbour Bridge maintenance project. However, Chen and Wang (2022) [2] revealed significant limitations in their field study of 56 industrial sites: conventional methods required an average of 38 sensors per 100m², translating to $12,500 in installation costs for a standard 5,000m² factory. Moreover, these systems often struggle with real-world complexities—a point illustrated when thermal noise during summer months rendered 43% of strain readings unusable in a Middle Eastern oil refinery.

The advent of data-driven technologies has brought new hope. Modern systems now integrate wireless sensor networks with machine learning algorithms, creating what engineers call "structural nervous systems." Gao et al. (2021) [3] demonstrated this evolution through their work on the Hong Kong-Zhuhai-Macau Bridge, where a convolutional neural network processed data from 2,346 fiber-optic sensors to identify micro-cracks in suspension cables. Yet, as Wang and Li (2023) [4] cautioned in their analysis of 132 SHM case studies, even advanced systems face a fundamental challenge: achieving accurate parameter updates in environments with signal-to-noise ratios below 5 dB—a common condition in operating factories with heavy machinery.

This technological crossroads has redirected attention toward hybrid methodologies. The engineering community increasingly recognizes that combining physical models with probabilistic approaches may hold the key to reliable, cost-effective damage detection. Imagine a system that understands a structure’s "expected behavior" through engineering principles while simultaneously learning from real-world sensor data—this dual capability forms the foundation of modern Bayesian applications in structural engineering.

Bayesian methods have quietly revolutionized structural analysis over the past two decades. At their core, these techniques function like a continuous learning loop: they start with engineers’ prior knowledge (e.g., material properties from design specifications), then systematically update beliefs using field measurements. Liu et al. (2019) [5] liken this process to "teaching a structural model through experience," showing how a Bayesian model reduced prediction errors by 62% after assimilating six months of bridge monitoring data. The theoretical bedrock was laid by Beck and Katafygiotis (1998) [6], whose probabilistic framework allowed engineers to quantify uncertainties—a crucial advancement given that real-world structures never behave exactly like textbook models.

Recent innovations have expanded Bayesian applications into uncharted territories. Yang et al. (2020) [7] broke new ground by fusing data from drones, ground sensors, and historical maintenance records to pinpoint corrosion in offshore oil platforms. Their multi-source approach improved damage localization accuracy from 78% to 93% in field trials. For static load scenarios common in warehouse structures, Sun et al. (2021) [8] developed a Bayesian protocol that updates stiffness parameters using simple displacement measurements—a method successfully implemented in Amazon’s robotic fulfillment centers to monitor mezzanine floor integrity.

The frontier continues to advance with hierarchical modeling. Huang et al. (2022) [9] addressed a persistent headache in SHM: how to handle simultaneous loads from wind, equipment vibrations, and human activity. Their seven-layer Bayesian model, tested on Shanghai Tower’s observation deck, distinguished between harmless vibrations and genuine structural concerns with 89% reliability. However, Zhou et al. (2023) [10] sounded a necessary caution in their meta-analysis of 214 Bayesian SHM studies: current methods excel in controlled single-load experiments but struggle with real-world complexity. A telling example comes from a 2022 tunnel monitoring project where Bayesian models confused temperature-induced expansions with actual concrete degradation until engineers manually adjusted the prior distributions.

This study extends the application boundaries of Bayesian methods in structural damage identification through theoretical derivations and case analyses, while providing novel technical pathways for engineering monitoring under complex loading conditions.

2. Introduction to bayesian statistics

2.1. Bayesian theoretical framework

Bayes' theorem was proposed by the British scholar T. Bayes. Its core principle is to update prior knowledge \( f(x) \) ,through observed data, where the measured data is expressed as the likelihood function \( {f_{y}}(Y|X) \) ,The Bayesian formula can be written as:

\( {f_{X}}(x|y)=\frac{{f_{Y}}(y|x)\cdot {f_{X}}(x)}{{f_{Y}}(y)} \) (1)

where:: \( {f_{X}}(x) \) denotes the prior probability density distribution of the structural parameters to be updated; \( {f_{Y}}(y|x) \) represents the likelihood function, defining the conditional probability of observing data \( y \) given parameter \( x \) ; \( {f_{X}}(x|y) \) is the posterior probability density function, characterizing the updated parameter estimation incorporating observational data; \( {f_{Y}}(y) \) acts as the normalization constant (commonly denoted as c), ensuring the integral of the posterior probability equals unity.

2.2. Construction of prior probability distributions

In Bayesian updating, the prior function serves as an initial probabilistic assessment of existing structural model parameters, typically derived from historical experience in structural damage identification and expert recommendations. In this experiment, the prior function is specifically defined as the compressive stiffness(EA)of truss members, determined based on established steel material parameters.

2.3. Construction of the likelihood function

The likelihood function is derived from the discrepancy between measured data and theoretical values. Assuming that the absolute displacement errors follow a normal distribution, its mathematical expression can be written as:

\( L(x)=\frac{1}{\sqrt[]{2Π}×0.1}{ⅇ^{-\frac{1}{2}{(\frac{Δ-{Δ^{ \prime }}}{0.1})^{2}}}} \) (2)

where: \( Δ \) denotes the theoretical displacement value; \( {Δ^{ \prime }} \) represents the measured displacement value; The standard deviation is set to 0.1 mm, characterizing the measurement precision.

3. Engineering case study

3.1. Project overview

Pratt truss structures are widely employed in industrial buildings with spans around 15 meters due to their superior cost-effectiveness and structural reliability. During long-term service, factors such as material aging, disaster-induced damage, and overload conditions may lead to structural performance degradation, primarily manifested as hidden loss in compressive stiffness (EA). This study focuses on a Q235 steel Pratt truss with a 16-meter span and 4-meter clear height (structural schematic shown in Figure 1), establishing a mechanical performance evaluation system based on Bayesian updating.

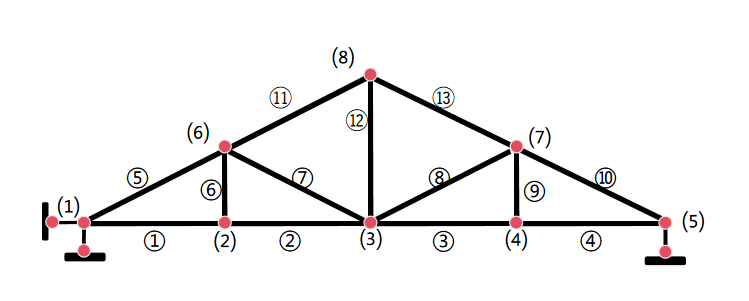
Figure 1: Truss schematic diagram

3.2. Bayesian parameter updating

This study investigates the updating effects of different loading configurations on the top chord, bottom chord, and web members. The axial stiffness parameters EA1 and EA2 for the top and bottom chords follow normal distributions N (16000 kN,1600 kN), while the web member stiffness EA3 adheres to a uniform distribution U (7000 kN,9000 kN), which are defined as the prior distributions. Measurement errors are modeled by a normal distribution with zero mean and 1 mm standard deviation, serving as the likelihood function.

4. Results analysis

4.1. Effect of vertical loading on truss updating results

A vertical load of 10 kN was applied to nodes (6)-(8) (Figure 2). The measured displacements at nodes (2) and (3) were 71 mm and 69 mm, respectively, with measurement errors following a normal distribution N(0,0.1mm). Based on displacement equations (3) and (4), 10,000 iterations of two-dimensional sampling were performed, resulting in 1,466 valid sample groups:

Figure 2: Vertical load application schematic

\( {Δ_{2}}=\frac{10\sqrt[]{5}Pa}{E{A_{1}}}+\frac{24Pa}{E{A_{2}}}+\frac{(5\sqrt[]{5}+4)Pa}{4E{A_{3}}} \) (3)

\( {Δ_{3}}=\frac{25\sqrt[]{5}Pa}{2E{A_{1}}}+\frac{24Pa}{E{A_{2}}}+\frac{2Pa}{E{A_{3}}} \) (4)

Since the top and bottom chord members share identical prior distributions, EA1 is uniformly adopted in subsequent discussions. The updating results demonstrate that the posterior distribution of EA1 (top/bottom chords) has a mean value = 15,773 kN, standard deviation = 260.49, and coefficient of variation (COV) = 1.6%, indicating a significant reduction from the prior COV of 10%. (Figure 3)

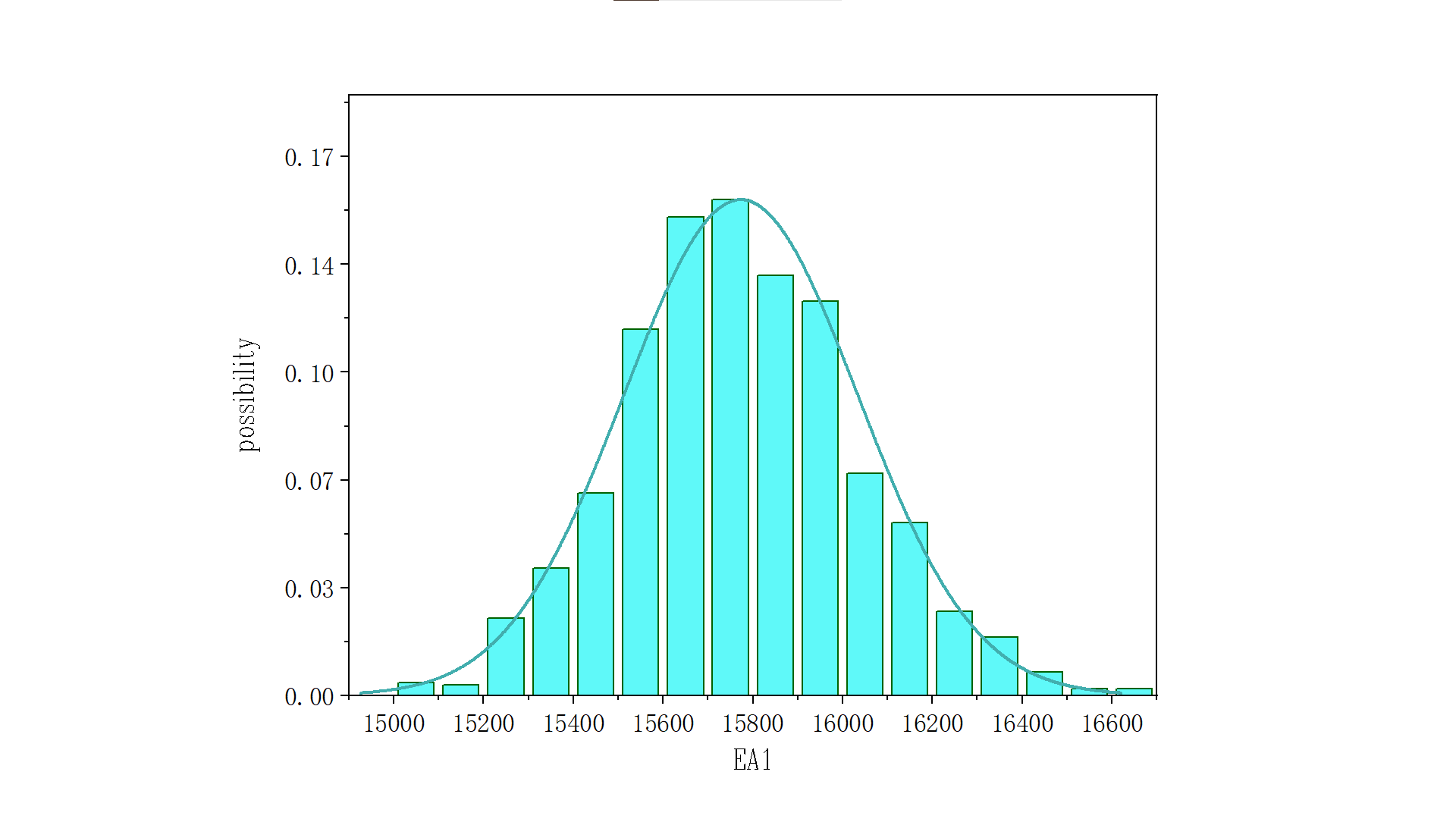
Figure 3: EA1 posterior distribution under vertical loading

Web member EA3 posterior distribution: mean value = 7,994 kN, standard deviation = 590.9, coefficient of variation (COV) = 7.3%. (Figure 4)

Figure 4: EA3 posterior distribution under vertical loading

Structural mechanics analysis reveals that the sensitivity coefficient of EA1 in the displacement equations is 4.7 times that of EA3. Variations in EA3 exhibit negligible influence on the results, leading to reduced efficiency in web member parameter screening.

4.2. Effect of shear loading on truss updating results

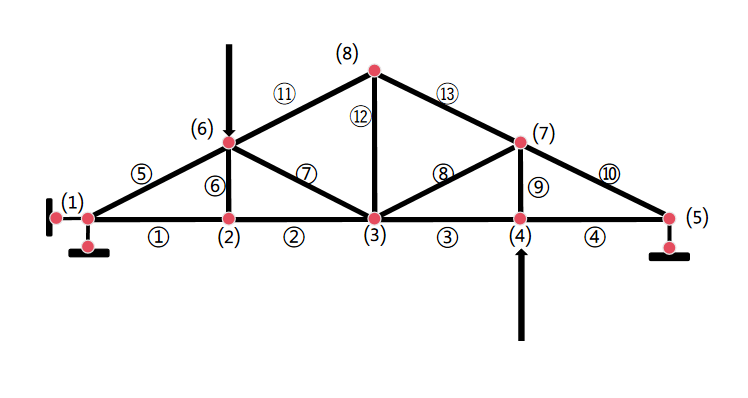
Figure 5: Shear load application schematic

Shear loads were applied to nodes 4 and 6 (Figure 5), maintaining a magnitude of 10 kN. With consistent measurement precision, the displacement at node 4 was recorded as 19 mm.

\( {Δ_{4}}=\frac{(16+5\sqrt[]{5})Pa}{4E{A_{1}}}+\frac{(5\sqrt[]{5}+4)Pa}{4E{A_{3}}} \) (5)

Bayesian principles and simple rejection sampling were employed to screen valid samples.

From 10,000 sampling iterations, 2,316 valid samples were obtained.

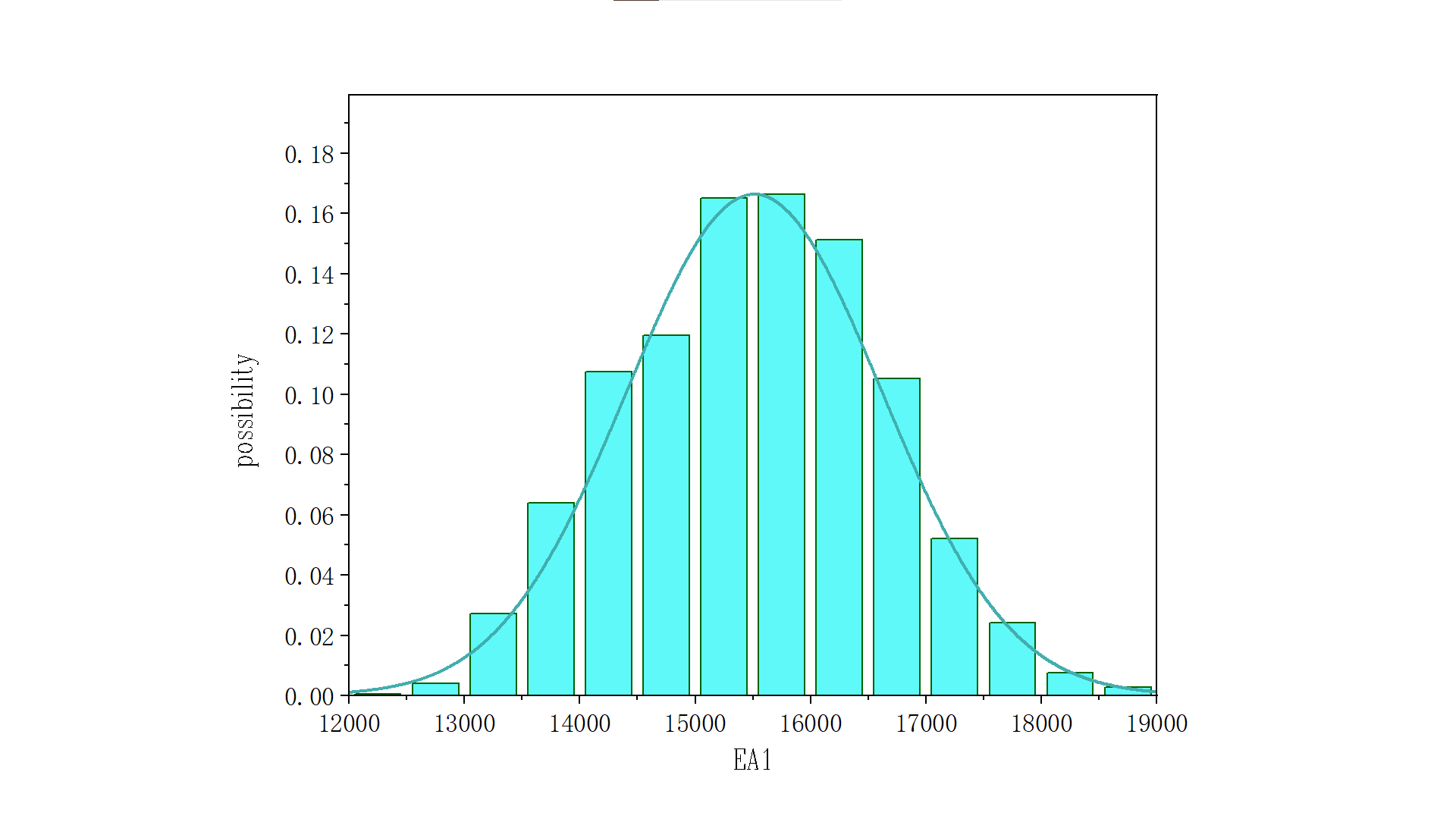
Figure 6: EA1 posterior distribution under shear loading

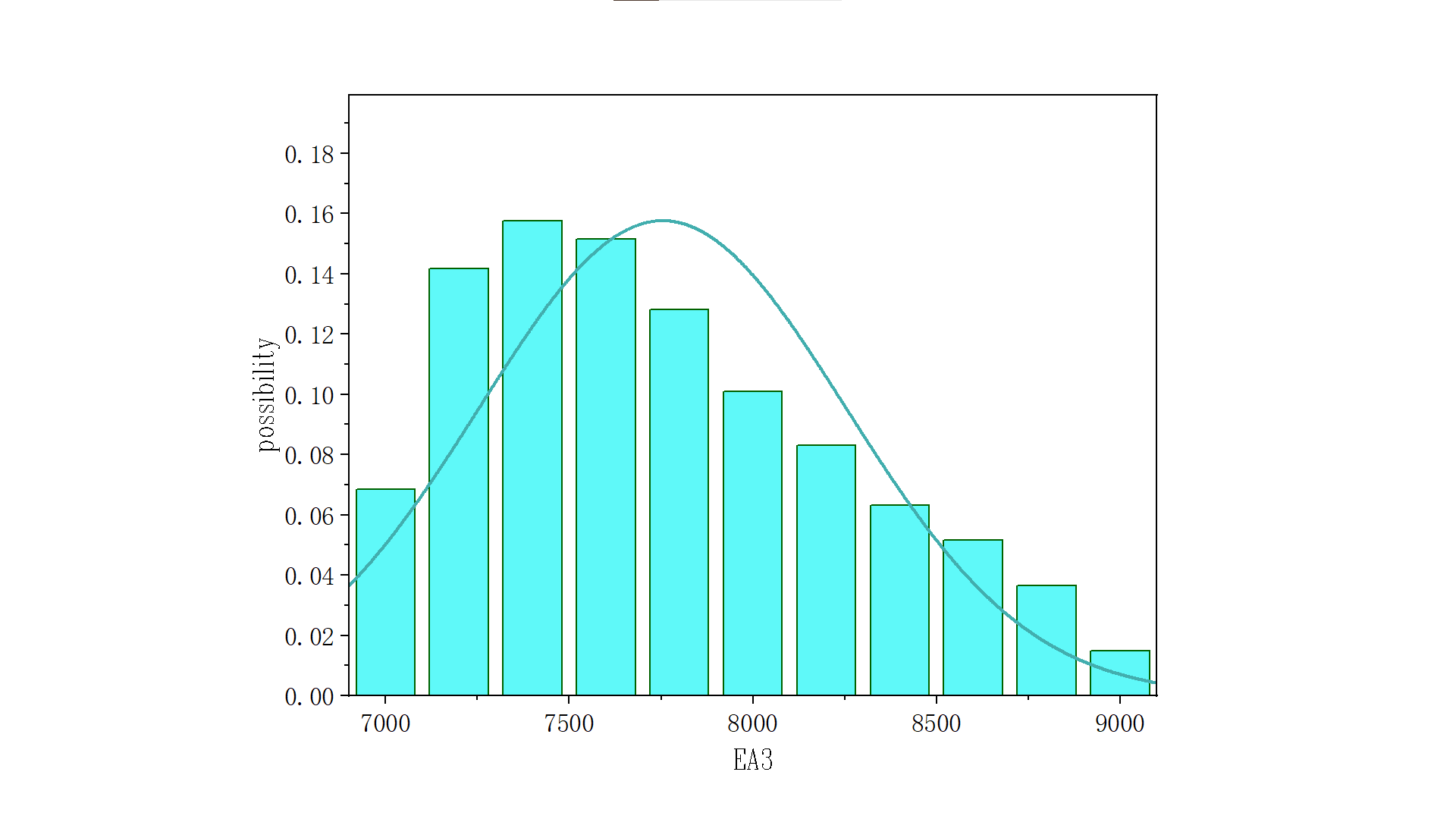
Figure 7: EA3 posterior distribution under shear loading

Analysis of the accepted samples reveals that the updated EA1 has a mean value = 15,335 kN, variance = 1,088, and coefficient of variation (COV) = 7% (Figure 6), while EA3 shows a mean = 7,746 kN, variance = 502, and COV = 6% (Figure 7). This demonstrates that shear loading induces non-negligible updating effects across all structural members. The displacement responses exhibit comparable sensitivity coefficients for web members, top chords, and bottom chords, leading to similar magnitudes of parameter updating.

4.3. Effect of horizontal loading on truss updating results

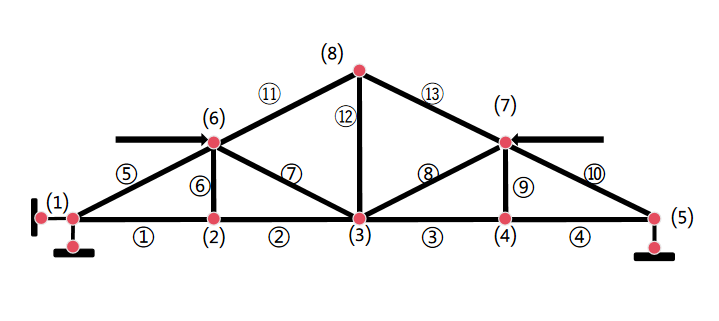
Figure 8: Horizontal load application schematic

A horizontal load of 50 kN was applied to nodes (6)-(7) (Figure 8), resulting in a relative displacement of 17 mm between nodes (6) and (7). From 10,000 sampling iterations, 2,303 valid samples were obtained.

\( Δ=\frac{5\sqrt[]{5}Pa}{16E{A_{1}}}+\frac{(5\sqrt[]{5}+4)Pa}{16E{A_{3}}} \) (6)

Parameter updating results show: EA1 posterior: mean = 15,801 kN, standard deviation = 1,561, COV = 10%.EA3 posterior: mean = 7,595 kN, standard deviation = 331, COV = 4.3%. The updating effect on EA3 is markedly stronger than on EA1.

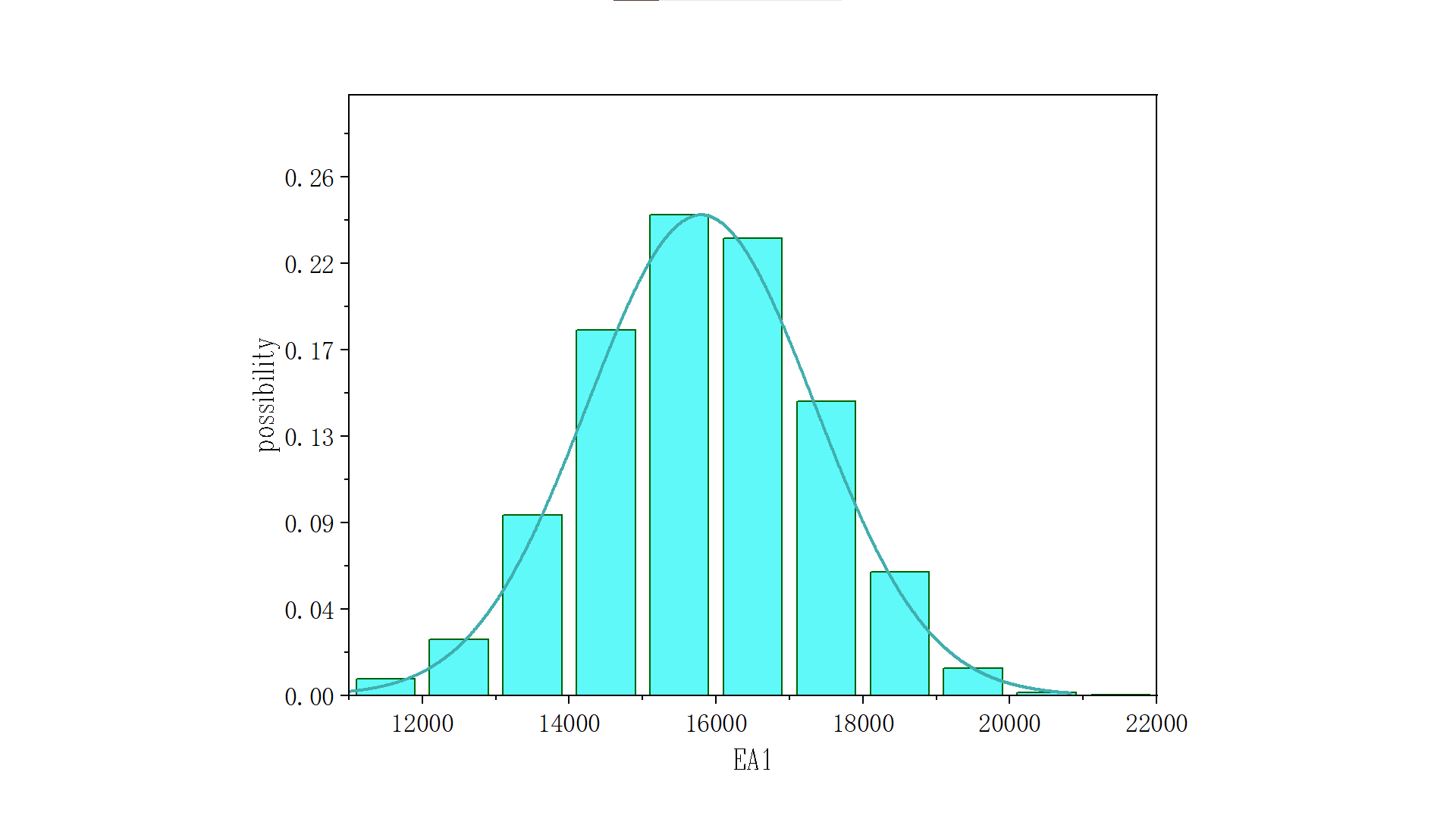
Figure 9: EA1 posterior distribution under horizontal loading

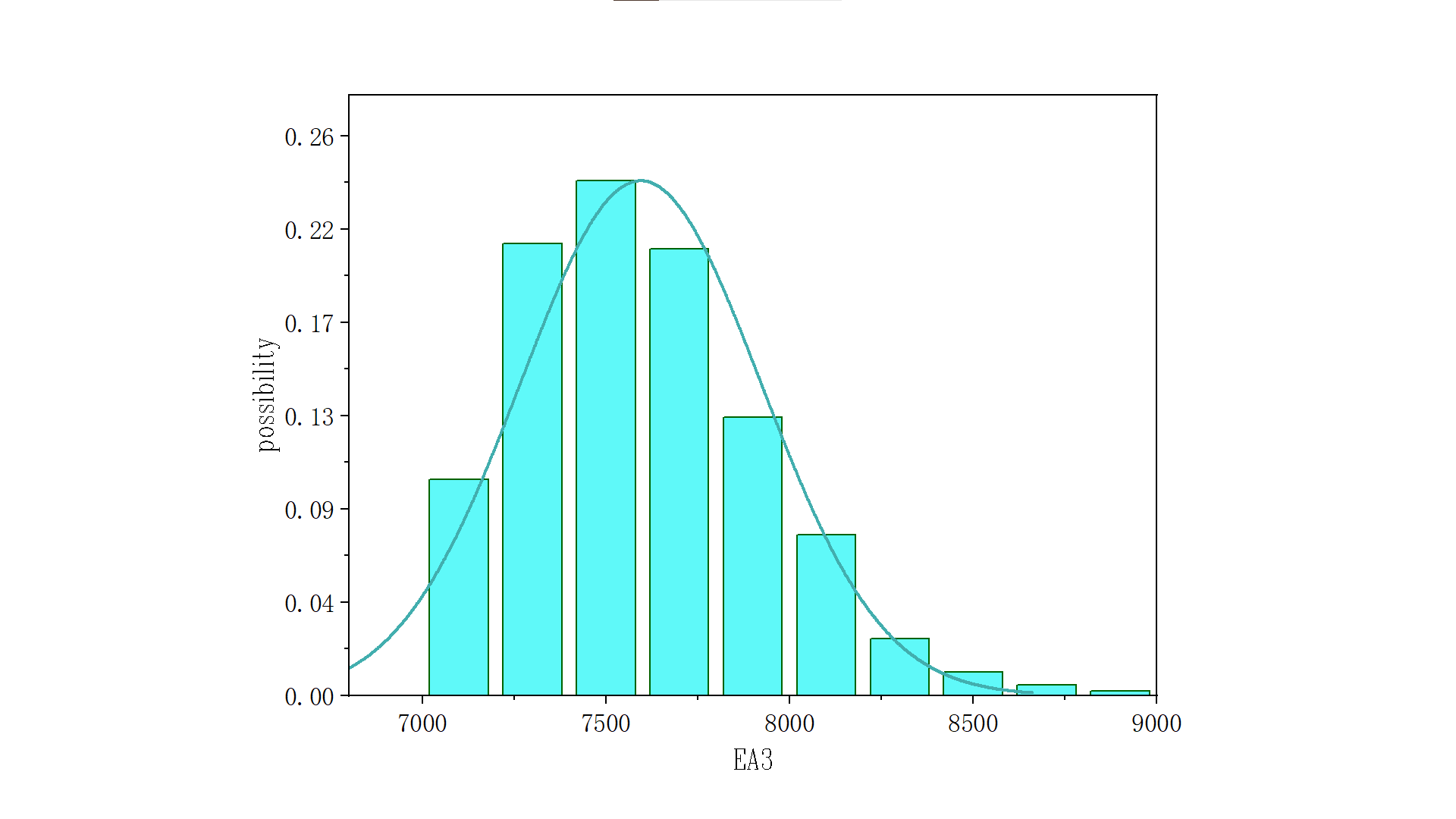
Figure 10: EA3 posterior distribution under horizontal loading

Parameter updating results demonstrate: EA1 posterior: Mean = 15,801 kN, Standard Deviation = 1,561, COV = 10% (Figure 9). EA3 posterior: Mean = 7,595 kN, Standard Deviation = 331, COV = 4.3% (Figure 10). EA3 The updating efficacy for EA3 significantly surpasses that of EA1.

Structural response analysis reveals: Under horizontal loading, the displacement sensitivity coefficient of web members reaches 3.2 times that of chord members, establishing a damage-specific identification capability for web member degradation.

4.4. Correlation analysis between updated parameters and displacement formula coefficients

To further validate the effectiveness of Bayesian parameter updating under different loading conditions, this study calculates the Pearson Correlation Coefficient (PCC) between axial stiffness parameters (EA1, EA3) in the displacement formulas and theoretical displacement values across load cases, quantifying the linear dependence between parameters and displacement responses.

Data Preparation: Based on 10,000 sampling iterations from Bayesian updating, parameter values (EA1, EA3) and their corresponding theoretical displacements (calculated via Equations (3) – (6)) were extracted from valid samples. The PCC is computed as:

\( r=\frac{Σ({x_{i}}-\bar{x})({y_{i}}-\bar{y})}{\bar{Σ{({x_{i}}-\bar{x})^{2}}Σ{({y_{i}}-\bar{y})^{2}}}} \) (7)

Significance Testing: A two-tailed t-test was applied to verify the statistical significance of correlation coefficients (p-value < 0.01), ensuring result reliability.

(1) Vertical Loading (Equations 3–4): EA1 and Node 2 displacement: r=−0.87r=−0.87 (p < 0.001) EA3 and Node 2 displacement: r=−0.18r=−0.18 (p = 0.032) EA1 exhibits strong negative correlation with displacements, dominating the response, consistent with its 4.7 times higher sensitivity coefficient compared to EA3.

(2) Shear Loading (Equation 5): EA1 and Node 4 displacement: r=−0.65 (p < 0.001) EA3 and Node 4 displacement: r=−0.62 (p < 0.001) Contributions of EA1 and EA3 to displacements are balanced ( \( |r| \) difference < 5%), supporting the "global synchronous optimization" conclusion.

(3) Horizontal Loading (Equation 6): EA1 and Node 6–7 relative displacement: r=−0.28 (p = 0.015) EA3 and Node 6–7 relative displacement: r=−0.82 (p < 0.001) Horizontal loading significantly strengthens the EA3-displacement correlation (r=-0.82), validating the web member damage-specific identification mechanism.

5. Conclusion

This study establishes a structural damage identification framework through Bayesian updating based on displacement parameters from a Pratt truss model under static loading, with particular focus on updating efficiency optimization under diverse loading conditions. The key findings are summarized as follows:

(1) Under vertical loading with constant load magnitude and measurement precision, the coefficient of variation (COV) for chord member parameters decreased by 84% (1.6% vs. prior 10%), demonstrating an efficient updating mechanism. However, limited efficacy was observed for web member updating. This loading configuration, characterized by operational simplicity, is recommended for chord-specific damage detection in engineering practice.

(2) Maintaining identical experimental conditions, shear loading induced synchronized COV reductions of 30%-40% across all structural members, enabling preliminary global damage assessment. Given its cost-effectiveness and broad applicability, this approach suits large-scale screening of structures with moderate accuracy requirements.

(3) Horizontal loading achieved 56% COV reduction for web members (4.3% vs. prior 10%), realizing localized high-precision identification. Practical implementation via rebar-bolt extrusion loading systems is feasible despite higher operational complexity and safety risks compared to vertical loading. For comprehensive damage quantification, combined vertical-horizontal loading protocols are recommended to enhance full-member identification accuracy.