1. Introduction

While artists have long been composing music with their autonomous decisions, some instead explore the possibilities of creating music with minimal human intervention. Despite the connotation of computer programming implied by the word “algorithm”, algorithmic composition dates back long before the modern computer was popularized [1, 2]. The ancient Greeks, with Pythagoras as a representative, first made the connection between numbers and sound in their musical systems. These findings were applied to their musical decision-making regarding tonality and intervals, but the process of producing music has not yet become automated. “Canonic” composition allowed infinite variations to be automatically derived from one musical idea, a successful attempt in removing the composer from the compositional process. Some musicians also attempted alternatives, such as Mozart who composed “Dice Music” arranging small musical segments in random orders. A similar idea was later innovated in 1865 by John Clinton with his machine, the Quadrille Melodist, which used arrangements of cards with segments of music to generate quadrille dance music for performers who struggle with improvisation [3]. Under the cultural constraints of World War II, composers developed serialism to break free from traditional and historical references by parameterizing and manipulating music to the fullest extent possible [4].

The computer introduced a powerful new environment for algorithmic composition. One of the first attempts was Hiller and Isaacson’s Illiac Suite in 1957, which used computers to generate musical ideas, modify them with various functions, then filter the best results and assemble them into a full piece. This framework was later used in MUSICOMP, one of the first systems for automated composition. Later approaches mainly used stochastic or rule-based systems. Stochastic composition utilizes randomness in more complex ways than just rolling dice, such as deriving notes from statistical theory and Markov chains. Rule-based systems build a musical syntax out of many specific constraints, sometimes involving subroutines like that in MUSICOMP. Artificial intelligence was also later adopted in composition for their capability to learn new rules from source materials, but its “black box” mechanism deviates from the clarity of algorithms and is therefore not discussed in this paper [5, 6].

This study explored the potentials of using the random walk algorithm as a stochastic technique in algorithmic composition. Though the random walk has already been widely used in the music industry for music recommendations in online platforms, the notion of using random walk to directly generate music is still relatively unexplored.

To begin with, the random walk is generally used for other purposes instead of in the field of music. One example of this is using random walk to model the movement of individual organisms in biology. In fact, Brownian motion, a basis of random walk, was first observed in the irregular movement of pollen by botanist Brown [7]. This simple model is uncorrelated and unbiased, meaning that the motion is independent of the object's position and the motion has equal chance of moving in any direction. A more complex random walk could be correlated, such as giving it a tendency to continue moving in a similar direction, useful for simulating the migration of animals as they move along a relatively straight path. Adding bias to a random walk can be used to simulate the effect of environmental factors on individuals, such as the distribution of microorganisms under gravity or the path of animals searching for food. In addition, the article addresses potential limitations of the random walk model, the most significant being the theoretical possibility for a random walk to move indefinitely away from the origin, which does not occur in most real scenarios.

Narrowing down its application to the music industry, random walk is also commonly used in music recommendation on various online platforms. One article introduces a Multi-Scale HyperGraph Node (MSHN) Embedding approach to music recommendation with random walk [8]. In essence, a weighted random walk algorithm is deduced from the user's listening preferences, then used to predict music that would fit their needs.

The most relevant and accessible work using random walk was a paper on building chord progressions with random walk in Neo-Riemannian spaces. Neo-Riemannian theory is a novel yet often overlooked branch in music theory that explains unconventional chord progressions with certain transformations that connect major and minor chords. The Neo-Riemannian space in which the random walk takes place is a network with all chords connected by such transformations. By following a walk through the network, a coherent chord progression that does not adhere to any fixed key can be heard [9]. The paper described how training a parameterizable random walk in Neo-Riemannian space generates chord progressions with unique textures concurrently.

It was found that the random walk algorithm was not yet fully explored in the discipline of algorithmic composition. An initial idea was to map a random walk directly to the pitch of an instrument to generate melodies, as the structure of a melody is to some extent similar to the trace of a random walk. Relevant works revealed that random walks can take place not only along a single axis, as in the initial idea with pitch, but also in 2-dimensional planes, along networks, and even in multiple dimensions. However, holding on to the belief that the simplicity of a notion does not render it less academically valuable, the exploration of directly generating pitch patterns using random walk was continued.

The framework of this study rooted from a basic random walk along one dimension with a fixed set of possible step lengths and an equal chance of stepping in the positive and negative directions. This random walk was directly mapped to the pitches of a synthesized instrument. Then, more constraints were introduced, including a tendency mask as a function of time to create melodic contour and quantization to specific pitches for harmony and cohesion. This served as an integration of stochastic generation and rule-based composition. Finally, this paper presents a worked example that uses this model as well as a rationale on its production.

2. Methodology

2.1. Principles

The main principle applied in this project is the random walk algorithm. A random walk is a path composed of random steps with random directions and length within a certain space. The random walk algorithm has already been widely applied in the field of biology to model the movement of microorganisms in 3-dimensional space and in the field of music for generating chord progressions according to predefined networks of chords or music recommendations based on user preferences. However, it has not yet been used to generate melodies. It was speculated in this study that it would be reasonable to do so because a comprehensible melody is fundamentally a walk of pitches with step length of certain intervals aligned to a rhythm.

The simplest way to generate a sequence of pitches with random walk is to start from a given pitch and change it by a random step length (interval) in a random direction. Yet, there are some aspects of this generic random walk that makes it unsuitable for directly applying to melodic composition. First, this random walk does not have a boundary. In rare circumstances, the random walk would traverse to extremely high or low values, exceeding the adequate range for a melody or even the range of the instrument itself. Second, the outcome of picking random intervals is most likely atonal, meaning it does not conform to any fixed key or progression, leading to dissonance when composing a piece with established harmonies. In order to constrain the random walk to specific ranges and keys or chord progressions, a tendency mask was used to bias the random walk and quantization was performed on its output [8].

A smart implementation of the "sref" and piecewise linear functions in Nyquist make the tendency mask that defines the correlation and bias in this random walk so it does not go out of the bounds of an instrument’s pitch or beyond its specified register. To elaborate, the "sref" function gives the amplitude of a sample at a given point in a sound. Envelopes constructed by the piecewise linear function are also stored as sounds in Nyquist. Therefore, "sref" can output the value of a piecewise linear function given an arbitrary number input. In this case, the input would be the current position of the random walk, and the output, a float between 0 and 1, the probability of the next step going up. Otherwise, the step will go down. The implication is that a decreasing piecewise linear function will naturally constrain, with probability, the range of pitches the random walk can move in (seen from Fig. 1).

Figure 1: An example of a tendency mask. The random walk will be constrained to the range of 76-88 and incline towards 82 where the probability of going up or down is 50% (photo/picture credit: original)

Using a similar principle, another piecewise linear function can be used to transpose the tendency mask over time to shape a melodic contour. If used extensively, this can be a very powerful tool, but the worked example in this paper sticks to a relatively simple application of guiding the macroscopic direction of the random walk [9].

2.2. Data

The final product was composed of four instances of the random walk function, with parameters as listed in Table 1. Pitches are notated with C4 being equivalent to 60 and each difference of 1 being a semitone in 12 tone equal temperament. “pwlv(a, b, c, d, e…)” is a Nyquist function that denotes a piecewise linear function with (0, a), (b, c), (d, e)… as vertices. Chords are notated using chord names, with “S” representing “sharp”. For example, “FSm” represents a F-sharp minor triad. The unit of time is seconds.

Table 1: Parameters used for generating the final product

2.3. Software

This project used the SAL programming language in Nyquist [10], a powerful language specialized for computer music synthesis and composition, as it integrates signal processing and sound synthesis. In comparison with other mainstream programming languages, SAL puts greater emphasis on functions, defining and nesting multiple commands to create complex effects instead of using a linear chain of commands. Its many built-in functions proved to be essential for achieving the goal of this project. The tool "score-gen" was used to construct a playable score from several parameters. Patterns in Nyquist offered an efficient way of constructing endless lists that recorded the pitch and rhythm. A smart implementation of the piecewise linear functions and “sref” was essential to building the tendency mask that guides the trend of the random walk. The “#?” operator, exclusive to Nyquist and capable of writing an if-else statement into a single line, was central to determining the direction of the random walk. At last, the “score-play” and “score-write” functions were used play the score and convert the score into MIDI files respectively. The resulting MIDI file was opened and visualized in FL Studio with a piano roll.

3. Results and discussion

3.1. Process

The random walk function accepts nine parameters: starting pitch (start), the tendency mask that biases and constrains the random walk (mask), the list of step lengths to randomly pick from (step), the list of the chord progression to quantize to (prog), the chance of not quantizing thus deviating from this chord progression (deviation), the trend or contour of the random walk (trend), the range in which this contour occurs (range), the number of steps this random walk would take (length), and the inter-onset-interval between each note in the final generated score (minioi). Before the loop for random walk begins, the function creates a list beginning with “start” for recording pitches generated from the random walk, which will be sent to “score-gen” to generate a playable score. A pattern that cycles through the “step” list randomly is made using the function “make-heap”. A float “k” between 0 and 1 keeps track of the current progress in generation.

A loop then performs the random walk until the list of pitches contains “length” elements. The walk first identifies the current pitch with the last element in the list of pitches and the current chord by finding the element in “prog” that matches the current range of “k” values. Then, “k” is advanced, and the “mask” is transposed according to “trend”. As piecewise linear functions are immutable in Nyquist, this transposition is reflected with a “shift” variable that is later used to offset the point “sref” references from the “mask”. To determine the next pitch to append to the list, the function first references “mask” to find the probability of walking up or down, then rolls a random number accordingly to decide. The function finds the next pitch according to the next element in the pattern of step lengths, then determines whether to quantize the next pitch to the chord given by “prog” according to the probability named “deviation”. If chosen to quantize, the next pitch value would be set to the nearest pitch that is in the designated chord. This is done by referencing and picking the nearest integer from a function that converts chord symbols of all major and minor triads to a set of integers that represent the modulus of pitches in the chord by 12, outlining chord tones regardless of octaves then returning the pitch to its original octave outside the function. For example, when quantizing the pitch 60 to a CS (C sharp major) triad represented by {1 5 8 13}, it is first divided by 12 to get 5 with a remainder of 0. Then, the number in the set closest to 0 is found (1), then added back its 5 octaves (60) to get 61. This final pitch obtained is appended to the list of pitches, and the procedure above is repeated.

Finally, the list of pitches is made into a pattern for “score-gen” to convert and return as a score. A simple worked example was made to demonstrate the robustness of this model with different parameters. This worked example was inspired by Canon in D, where various parts join in and accompany the melody in harmony throughout the piece. This structure was very easy to achieve in Nyquist using the score-merge and score-append functions by merging the parts for each stanza and joining together the stanzas. Four instances of the random walk were built, one as a bassline, one as the main melody, and the other to as fast arpeggios in the high register. The four stanzas in this score introduce the four parts in ascending order by pitches.

3.2. Evaluation

This worked example is approximately 40 seconds long. As shown in the Fig. 2, the bassline, melody, and two arpeggios are clearly distinguishable by the registers they occupy and the length of notes. There is also a noticeable V-shaped, especially in the arpeggios, which was a result of the “trend” and “range” parameters. The bassline is most constrained, strictly following a stepwise pattern along the designated chord progression. The slight deviation applied in the melody proved to be successful, as it allowed for a variety of melodic embellishments that enhanced consistency and variety without breaking the harmony. The extremely fast arpeggios added an energizing harmonic texture to this piece.

There were some unintended octave jumps, such as the most noticeable gap in the melody, that likely occurred due to unconsidered edge cases in the quantization program. More meticulous testing is necessary to find the root cause and resolve this issue. Some notes ended up overlapping with other parts or repeating themselves too often. This could simply be solved with adjustments in the tendency masks. While the even rhythm suited this Canon-inspired piece quite well, it might not rise to the demand of other genres. Applying rhythmic changes would require reworking the way pattern length is kept track of in the function.

While this model demonstrated a new way of using random walk in generating melodies, it is not yet as elaborated or robust as many other more well-known models. This model is not yet capable of composing entire pieces, but may serve as a tool for creating unique accompaniments for certain contexts.

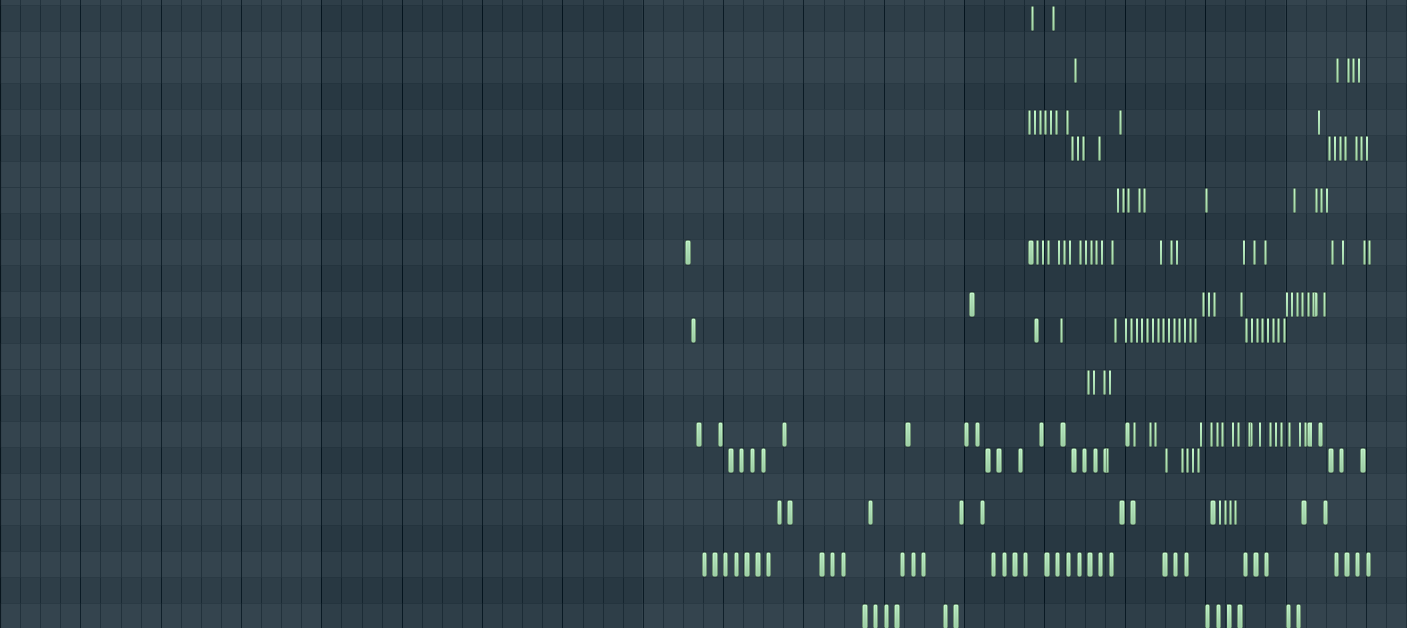
(a)

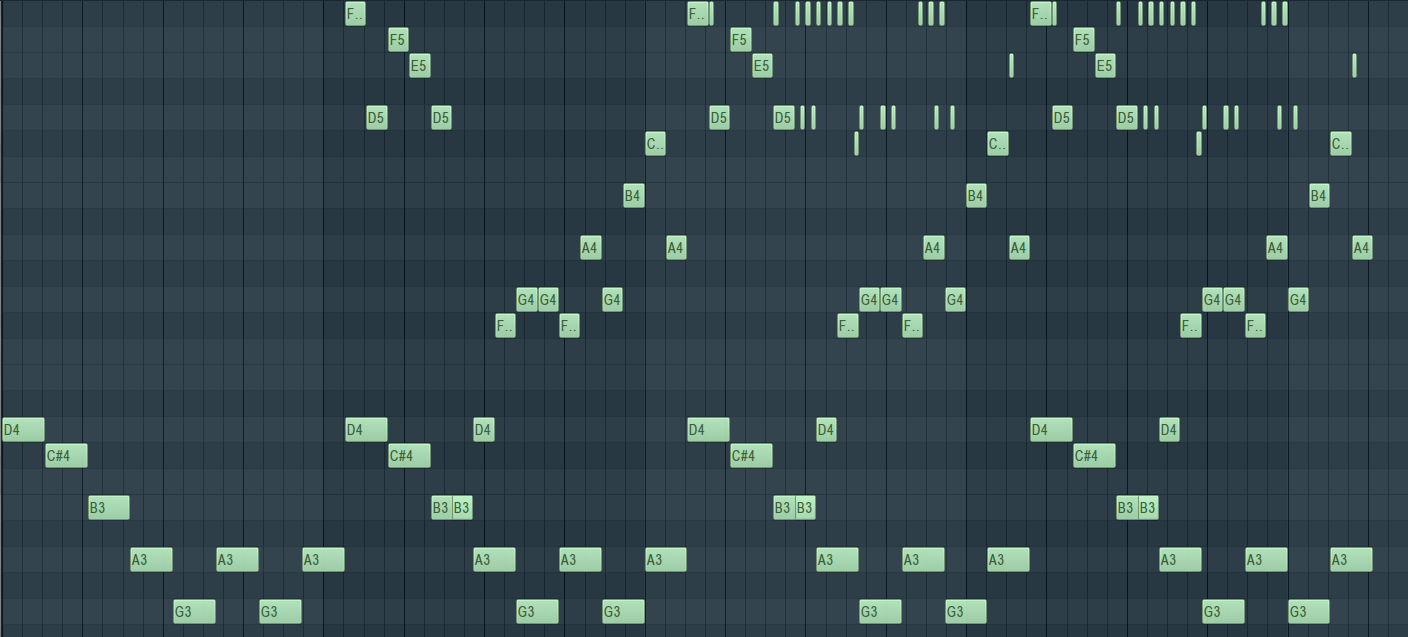
(b)

Figure 2: The exported MIDI file open in FL studio, split into (a) and (b) due to its massive range (photo/picture credit: original)

3.3. Limitations and prospects

Further enhancements to the model were considered in the development process but not yet achieved given the limited time for research. One was the addition of rhythmic changes in the form of arranging common rhythmic patterns. This would introduce some other potential rules, such as a contour for note density so rhythms can get simpler when approaching cadences, or markings for downbeats so these pitches are always quantized for reinforced harmonies. More chords other than major and minor triads could be made possible in quantization, such as the commonly found sevenths chords. Tendency masks for specific contexts may be applied to each chord, such as how basses are more likely to choose the root of each chord instead of a weaker inversion or extension. As an extension, a network of chords and progressions can be built and traversed, similar to the Neo-Riemannian method. When developed to its fullest extent, this model may look like a choreographed dance of multiple random walks and tendency masks in multiple dimensions, guiding each macroscopic and microscopic aspect of the music in complex but interpretable ways that can also be manipulated with parameters.

This study focused on algorithmic music generation based on random walk, aiming to provide a low-cost and intelligent background music solution. In the future, this technique can be applied to short videos, games, and independent films, automatically generating music that matches the scene while reducing production costs and enhancing content creation. By optimizing the algorithm, the system is expected to achieve greater stylistic diversity and user control, catering to personalized needs. Moving forward, the model will be refined based on user feedback to improve music quality and the complexity of this model and explore possibilities for real-time generation and interactive audio. This could lead to broader applications in virtual reality and adaptive soundtracks, making music production more accessible and efficient.

4. Conclusion

Using the random walk algorithm and quantization in Nyquist, this study found a relatively unexplored approach to algorithmic composition. While random walks have some fundamental flaws like its infinite possible range, tendency masks biased the probabilities in the random walk in ways that are beneficial for music composition. Linear functions proved to be effective in creating melodic contours. Pitches that lie outside the harmonic context of a piece of music were quantized to fit into given chord progressions. A worked example shows the potential of this tool in creating unique harmonic textures. Further exploration of this approach will likely develop this tool into a more established system capable of parameterizing many aspects of music production. These findings can be applied to many contexts where the spontaneous creation of music is demanded and to aid individual artists in their pursuit for inspiration.