1.  Introduction

Tom Mitchell points out in his book "Machine Learning" that machine learning is the process of "improving a performance measure of some task by getting a computer to observe its performance on examples from its environment and to learn from those examples how to perform the task in general". In other words, machine learning is the process by which computers use algorithms to explore the inherent patterns and extract information from data, thus gaining new experience and knowledge, and improving the intelligence of computers so that computers can make decisions similar to humans when facing problems [1].

In 1956, at the Dartmouth Conference, the field of artificial intelligence was born, and machine learning was proposed as an important research direction, marking the birth of machine learning as an independent research discipline. Over the following decades, this field evolved rapidly, giving rise to a diverse array of algorithms.

Currently, Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and Transformer models have achieved remarkable performance leaps in fields like computer vision (CV) and natural language processing (NLP). However, they face bottlenecks such as limited interpretability and data privacy concerns. This underscores the enduring research value of classical methods in terms of interpretability and computational efficiency. Systematically clarifying the intrinsic logic of algorithmic evolution can help prevent blind adoption of model selection. Focusing on supervised learning paradigms, this paper comprehensively reviews the evolutionary trajectory of machine learning algorithms from classical to modern approaches, filling the gap in systematic reviews of algorithmic evolution.

2.  Classical machine learning algorithms

2.1. Linear model

2.1.1. Linear regression

The core objective of linear regression is to learn the linear relationship between input features and target values, thereby constructing a predictive model for outputting predictions on new, unseen data. The model of linear regression:

$$$ \begin{array}{c}f\left(\overrightarrow{\mathrm{x}}\right)=\overrightarrow{\mathrm{w}\bullet }\overrightarrow{\mathrm{x}}+b\end{array}$$$(1)

 $$ \mathrm{f}\left(\overrightarrow{\mathrm{x}}\right)$$  is the predicted output of the model for the input  $$ \overrightarrow{\mathrm{x}}$$ .  $$ \overrightarrow{\mathrm{w}}$$  is the weight vector, with the same dimension as  $$ \overrightarrow{\mathrm{x}}$$ . It represents the degree of influence of input features on the output.  $$ \overrightarrow{\mathrm{x}}$$  is the input feature vector. b is the bias term.

A commonly used loss function in regression tasks is the mean squared error loss function, which is used to measure the error between the model's predicted values and the true values.

Suppose we have n samples. For the i-th sample, the true value is  $$ {\mathrm{y}}_{\mathrm{i}}$$  and the predicted value of the model is  $$ {\widehat{\mathrm{y}}}_{\mathrm{i}}$$ . The calculation formula of the mean squared error loss function is:

$$$ \begin{array}{c}MSE=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}{)}^2\end{array}$$$(2)

The core goal is to minimize this loss function, which can be achieved using gradient descent or the least squares method, thereby obtaining the linear equation.

2.1.2. Logistic regression

Linear regression is primarily used to predict scenarios where the labels are continuous. However, it has been discovered that regression can also be applied to classification scenarios, such as binary classification [2]. In binary logistic regression, the output label  $$ \mathrm{y}$$  belongs to either 0 or 1, while the linear regression model produces a real-valued prediction that needs to be converted into 0 or 1. In the logistic regression model, the sigmoid function is commonly used as the transformation function, as shown in Figure 1.

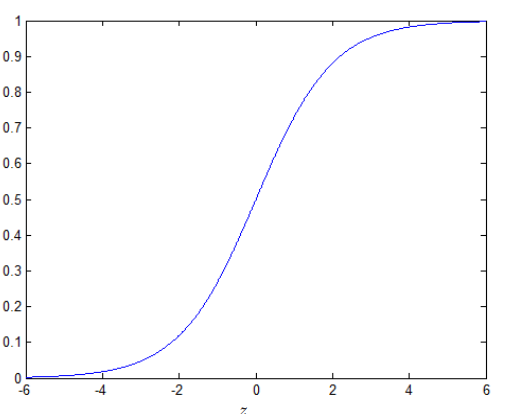
2.2. Support vector machine(SVM)

SVM is a generalized linear classifier that performs binary classification on data. Its decision boundary is the maximum-margin hyperplane derived from the learning samples [3]. The most important task of an SVM is to select the optimal decision boundary. The core idea is that the decision boundary should be as far away as possible from the data points of both classes. In other words, the goal is to find the separating hyperplane that maximizes the distance to the nearest data points from each class. The successful application of the support vector machine algorithm in the field of handwritten digit recognition shortly after its proposal fully demonstrates its significant theoretical advantages [3].

2.3. Decision tree and random forest

A decision tree represents the decision-making process through a tree-like structure, including the root node, decision nodes, branches, and leaf nodes [4]. The construction process of a decision tree includes feature selection, tree generation, and pruning [5]. The key to decision trees lies in selecting the optimal feature for splitting.

Common criteria include information gain and the Gini index. Information gain selects the feature that maximizes the reduction in uncertainty (entropy). The Gini index measures data impurity, with lower values indicating better splits.

Decision trees are intuitive and interpretable but prone to overfitting. Techniques like pruning can help mitigate this issue. Decision trees may perform poorly on complex data, while random forests significantly improve performance in such scenarios.

Random forest employs bootstrap sampling to construct multiple unpruned decision trees, where each node split selects the best variable from a randomly chosen small subset of features, achieving classification or regression through ensemble learning with dual randomization in both data and features [6].

For classification problems, random forest aggregates predictions from multiple decision trees via majority voting, where the class with the highest number of votes is selected as the final output. For regression tasks, random forest aggregates predictions from multiple decision trees by averaging their outputs, which serves as the final predicted value of the dependent variable.

3.  Modern machine learning algorithms

3.1. Fundamentals of neural networks and deep learning(DL)

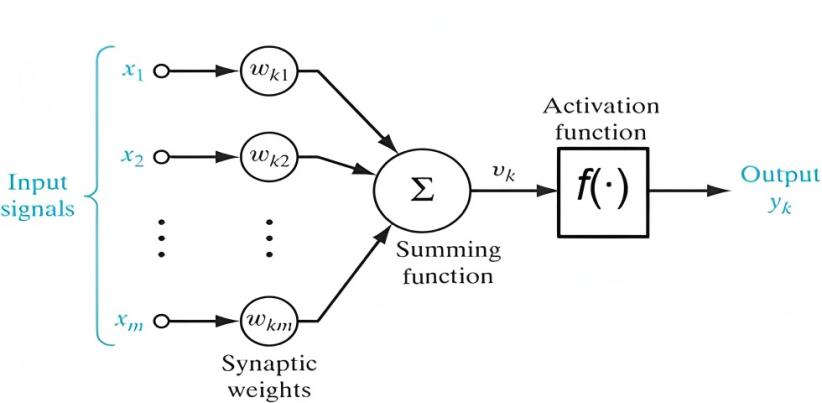
3.1.1. Artificial neuron model

The structure of the artificial neuron is shown in Figure 2. An artificial neural network neuron consists of three fundamental components: (1) Synaptic connections that receive inputs  $$ {\mathrm{x}}_{\mathrm{i}}$$  from previous neurons, each weighted by  $$ {\mathrm{w}}_{\mathrm{k}\mathrm{i}}$$ (where  $$ \mathrm{k}$$  is the current neuron's index and  $$ \mathrm{i}$$  is the input connection index); (2) a summing junction that computes the weighted sum of inputs, often including a bias term  $$ {\mathrm{b}}_{\mathrm{k}}$$ ; (3) an activation function that introduces nonlinearity by transforming the summed output  $$ {\mathrm{v}}_{\mathrm{k}}$$  into the neuron's final output  $$ {\mathrm{y}}_{\mathrm{k}}=\mathrm{f}\left({\mathrm{v}}_{\mathrm{k}}\right)$$ , enabling complex pattern learning.

$$$ \begin{array}{c}{\mathrm{v}}_{\mathrm{k}}=\sum _{\mathrm{i}}\left({\mathrm{w}}_{\mathrm{k}\mathrm{i}}\bullet {\mathrm{x}}_{\mathrm{i}}\right)+{\mathrm{b}}_{\mathrm{k}}\end{array}$$$(3)

$$$ \begin{array}{c}{\mathrm{y}}_{\mathrm{k}}=f\left({\mathrm{v}}_{\mathrm{k}}\right)\end{array}$$$(4)

3.1.2. Feedforward neural network (FNN) and Backpropagation (BP) algorithm

FNN, also known as the Multilayer Perceptron (MLP), is the most fundamental and classic neural network architecture. The neural network comprises an input layer that serves as the network's entry point, one or more hidden layers equipped with computational nodes responsible for processing and transforming the data, and an output layer containing computational nodes that produce the final results, with each layer sequentially passing information forward in a unidirectional flow without feedback loops, as shown in Figure 3. This structure forms the foundational architecture of a standard FNN, where data moves strictly from input through hidden layers to output.

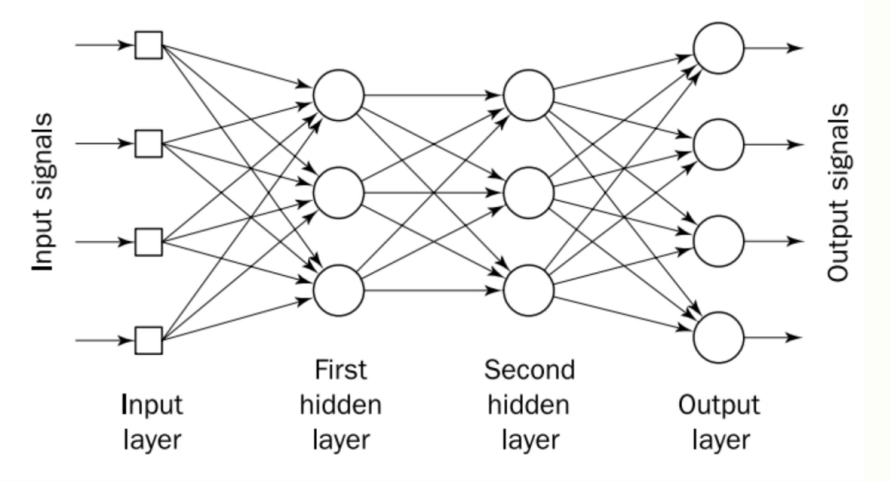
The BP learning process consists of two iterative phases: forward propagation, where input signals are processed through the network to extract features and produce output values, followed by backward propagation, where output errors are used to compute gradients and adjust network weights and biases via optimization methods. This alternating cycle of forward and backward passes continues until the network's output error converges within a predefined threshold, at which point the final weights and biases represent the learned features [1]. The entire process enables the network to progressively refine its accuracy by minimizing the discrepancy between actual and expected outputs.

3.2. Breakthroughs of neural networks and deep learning(DL)

3.2.1. Convolutional neural network(CNN)

A CNN is a type of multi-layer FNN with a convolutional structure. Unlike traditional fully connected FNNs, the core idea of CNNs lies in their use of local receptive fields and weight sharing to automatically extract hierarchical features from input data. This approach reduces the number of connections and parameters, lowering the complexity of the model and improving computational efficiency.

A CNN consists of an input layer, hidden layers, and an output layer. The hidden layers are composed of multiple pairs of convolutional layers and subsampling layers, while the output layer typically adopts a fully connected feedforward structure [1]. Each layer of the network contains multiple two-dimensional feature maps, and each feature map consists of numerous independent neurons [1].

The development of CNNs has gone through several milestone models: In 2012, AlexNet won the ImageNet competition for the first time, demonstrating the potential of deep CNNs through ReLU activation functions and GPU training; In 2014, VGGNet adopted the strategy of stacking 3×3 small convolutional kernels, establishing a positive correlation between depth and performance; in 2015, ResNet innovatively introduced skip connections, solving the training challenges of ultra-deep networks and pushing network depth to hundreds of layers; subsequent models like MobileNet and EfficientNet continued to innovate in the direction of lightweight design. These breakthroughs have made CNNs the core architecture in the field of computer vision and profoundly influenced the entire development process of deep learning.

3.2.2. Transformer architecture

The Transformer is a deep learning architecture introduced in 2017 by Vaswani et al. It revolutionized NLP and other sequence-based tasks by replacing traditional RNNs and CNNs with a purely attention-based mechanism.

The core innovation of the Transformer architecture lies in its multi-head self-attention mechanism, which excels at capturing relationships between elements in a sequence, particularly for modeling long-range dependencies [7]. By computing multiple attention heads in parallel, this mechanism learns diverse feature representations from distinct subspaces, significantly enhancing the model's capacity to handle complex patterns. Specifically, the advantages of multi-head self-attention are threefold. Firstly, the Query-Key-Value (QKV) mechanism allows direct interaction between any pair of elements in the sequence, eliminating the sequential computation bottleneck inherent in RNN-based models. Secondly, positional encoding explicitly integrates sequential order information into the model, compensating for the absence of inherent recurrence or convolution. Finally, layer normalization and residual connections help mitigate gradient vanishing in deep networks, ensuring stable training.

4.  Driving forces behind the evolution of machine learning algorithms

The evolution of machine learning algorithms is primarily driven by the synergistic breakthroughs in three key areas: data, computing power, and algorithms.

The widespread adoption of the internet has led to an exponential growth in data volume, providing the fuel for model training. Simultaneously, the shift from structured to unstructured data (e.g., images, text, and audio) has necessitated more powerful models to capture complex features.

The proliferation of GPUs and advancements in distributed computing have made it feasible to train large-scale models. Meanwhile, algorithmic innovations—such as the ReLU activation function, Dropout, Batch Normalization, and the Transformer's attention mechanism—have significantly enhanced model performance.

5.  Conclusion

This paper primarily explores the evolution of machine learning algorithms from classical to modern approaches. The study demonstrates that the rapid progress in machine learning has been predominantly fueled by the synergistic interplay of three key factors: the exponential growth of data, the remarkable advancements in computational power, and the continuous innovation in algorithmic design. However, the paper has not yet delved deeply into the ethical and security challenges in algorithmic evolution, such as interpretability and black-box risks, as well as data privacy and algorithmic misuse. Furthermore, the societal implications of algorithmic bias and the environmental costs of large-scale model training warrant deeper scrutiny. Although the trajectory of machine learning is nonlinear and fraught with challenges, it holds immense potential not only to drive scientific discovery but also to enhance human productivity, thereby advancing the sustainable development of global society.