1. Introduction

Unmanned Aerial Vehicles (UAVs) have experienced an increasing adoption of their use in areas like surveillance, delivery or disaster management due to their capability of operating autonomously in challenging and highly changing environments in order to generate paths.

The classic algorithms such as the A algorithm [1] achieve great results under static and fully observable conditions. Nevertheless, their applicability is limited since they are always dependent on accurate pre-known environment models. Real-world environments are often unknown or they are mutable in an arbitrary manner.

Reinforcement learning(RL) is an attractive model-free solution. The UAVs can autonomously learn to fly optimally through trial and error, i.e., without relying on any prior knowledge about the environment.

In this paper, we will conduct a thorough and comprehensive survey into applying RL to UAV path planning problem. Specifically, it will review various existing methods covering the traditional methods to recent deep learning based methods in a systematic and meticulous manner, and provide an overall summary of the pros and cons of those methods, and some useful suggestions and directions for future research efforts to design even better intelligent autonomous navigation systems.

2. Model for Reinforcement Learning in the path algorithm of Unmanned Aerial Vehicles

To apply Reinforcement Learning (RL) to UAV path planning tasks, a first and central step is to formally model the real - world problem (formally: an embedding as a Markov Decision Process (MDP)), a formalism naturally well-suited for sequential decision making in stochastic environments. This process of abstraction involves two key stages: designing the environment model and specifying the components of the RL process.

Then, an abstract description of the real world of the flight domain is designed [2]. The most common way to do this is to discretize the continuous three - dimensional space in order to get a discreted - grid - world, where one cell represents a state. This strategy can reduce the computation of the complexity, but then the paths might be sub - optimal and irregular. Another option is to use a continuos state - space representation.The latter approach provides an additional level of fidelity in the smoother trajectories but imposes high difficulties for learning algorithms since the number of states is infinite.

Once the environment has been modeled, the problem is characterized by the core elements of an MDP:

State (S): State s is an encapsulation of the agent’s and the environment’s state at one specific point in time. The minimum contents to inform must include the Cartesian position (x,y,z) and velocity, of the UAV and its heading. As the state is set to navigate more complex scenarios the state vector can be extended with other useful information for example to determine the energy remaining in the battery, the (relative) position of the target, sensor outputs (e.g. from a laser range finder or camera) representing potential obstacles.

Action (A): A’s the term action indicates a signal the UAV is able to perform. In a discretized model, the set of actions can be a finite list of preset maneuvers such as “move forward,” “take off,” etc. However, for additional control a continuous action space is used where actions directly affects the thrust, yaw, pitch and roll of the UAV.

Reward Function (R): The reward function acts as the learning cue, usually a large positive reward is given upon reaching destination and a large penalty is given when it collides or leaves the task region boundary, and an additional small negative reward per time step to encourage better paths and eliminate useless hovering.

Policy (π) : The policy π(a|s), characterizes the behavioral pattern of the UAV by establishing a mapping function from states to actions. The RL aims at determining a best policy, π^∗, with the highest overall reward for safely and effectively driving the UAV to desired destination.

3. Methods in Reinforcement Learning in Unmanned Aerial Vehicle path algorithms

After modelling the UAV path planning problem as a MDP, any reinforcement learning algorithms can be employed to search for the optimal policy. The evolution of these learning-based approaches in solving the path planning problem starts from classic tabular algorithms, then become more advanced deep-learning techniques, where the former caters to a small scale planning problem, while the latter allows tackling big data problems.

3.1. Classic Reinforcement Learning: Q-Learning and SARSA

Q-Learning and SARSA are two simple value-based, “tabular” RL algorithms [2]. They are based on the concept of maintaining a Q-table and storing the expected future reward (“Q-value”) for the state-action pair. During the training of the agent the interaction with the environment is followed by an update of the Q-values following the Bellman equation as follows:

$$ Q(s, a) \leftarrow Q(s, a) + \alpha [R + \gamma * max\_a\text{'} Q(s\text{'}, a\text{'}) - Q(s, a\left)\right]$$(1)

where α is the learning rate and γ is the discount factor.Q-learning is “off-policy” in that it updates with the maximum Q-value of the next state, greedily assuming some future action taken on behalf of it, irrespective of which action is practiced to explore. SARSA is “on-policy” because it updates with the Q-value of the actually-taken next action a’, and learns more cautiously.

However, the central flaw of these approaches is the ’curse of dimensionality’, limiting them to small, discrete and static worlds e.g. small grid-world examples.

3.2. Value-based deep Reinforcement Learning: DQN

Deep Q-Network (DQN) [3, 4] mitigates the problem of dimensionality curse in Q-Learning by approximating the Q-function with a deep neural network, which feeds a high-dimensional state (such as raw images) as input and predicts a Q-value for each discrete action. To help stabilize training, two mechanisms are used by DQN. One is Experience Replay: the agent collects experience tuples (s, a, r, s’) to form a buffer, and randomly samples mini-batches to train. The second point is that it breaks temporal correlations in the data and thereby improves the data efficiency. A Target Network: A secondary separate network, whose parameters are copied from the primary network at periodic intervals, is employed to calculate the target Q-value, This helps provide a steady target. that avoids the oscillatory nature of the training due to the simultaneous change in target and predicted values.

$y=r+\gamma \ast max\mathrm{\_}a\mathrm{\prime }Q\mathrm{\_}target(s\mathrm{\prime },a\mathrm{\prime })t$(2)

DQN and variants excel on high-dimensional perceptual states and discrete action spaces, so they can be used as the learning agent for navigation in highly cluttered and dynamic, such as indoor rooms and urban canyons [5].

3.3. Policy-gradient deep Reinforcement Learning: A3C

In contrast to DQN, policy-gradient techniques directly model and optimize the policy. A stateof-the-art representative is the Asynchronous Advantage Actor-Critic (A3C) algorithm [4]. It has Actor-Critic architecture: Actor is policy network that predicts a probability distribution over actions and Critic is value network, which predicts the state-value V(s) for the Actor’s decision.The Critic (roughly) directs the Actors updates by computing the advantage function which indicates the extent to which one action was improved or penalized compared to a default action. The key innovation of A3C is its asynchronous architecture: a batch of workers act in parallel, each accumulating experiences in its own environment copy and asynchronously back propagating gradients over a shared network, which massively accelerates training times.

$$ A(s,a)=Q(s,a)-V\left(s\right)$$(3)

A3C is a natural continuous action space agent, thus it is our first choice to use for dynamic environment where continuous smooth and accurate trajectory avoidance is required, for example, obstacle avoidance [6].

3.4. Other advanced Reinforcement Learning methods

Hierarchical Reinforcement Learning (HRL): HRL [7] decomposes a complex problem into a hierarchy of sub-tasks. A high-level policy sets abstract sub-goals, and a low-level policy learns to execute the actions to achieve them. This temporal abstraction effectively addresses large-scale, long-horizon navigation tasks with sparse rewards [8].

Imitation Learning (IL) and Inverse RL (IRL): These approaches [9] assume access to demonstrations. IL directly imitates the expert using supervised learning. IRL continues imitation by first estimating the hidden expert reward function. Both are suited to situations where it is hard to engineer the reward function but provide access to good-quality expert demonstrations well-suited to learning complicated behaviors.

4. Comparative analysis and discussion

In order to compare the performance of the aforementioned reinforcement learning algorithms for UAV path planning task systematically and fairly, in this section, we take some important performance metrics [10]. Such as path smoothness, planning success rate, ability to avoid dynamic obstacles, sample efficiency and data independence. The idea is to fully describe the characteristics and trade-offs of the different algorithms.

4.1. Performance evaluation index

Path Length. The path length is defined as the flight distance traveled by UAV between the start and end points. The path length is the direct and intuitive indicator for efficiency assessment of path plan. In terms of energy-limited UAV, the shorter the path, the less energy is consumed and the longer the endurance, which indicates a higher mission success rate.

Success rate. Success rate is defined as the ratio of number of runs (over a large number of independent runs), in which our algorithm was able to discover a safe collision-free path from start to goal in some environment. It indicates the trustworthiness and robustness of an algorithm. A high success rate implies that our algorithm is able to find a path of planning tasks across diverse, possibly unseen, layouts of environments.

Path smoothness. The change of the curvature of the synthesized path is used to quantify its smoothness. A smooth path enjoys a smooth curvature, and there will be no abrupt and discontinuous transition in the direction of the path. It is more comfortable and convenient for a real UAV to track and fly along the high smoothness path, which can avoid serious energy loss and mechanical wear by rigorous action and greatly improve the stability and safety of flight. The integral of heading angle changes or the integral of the curvature profile along the path are the key indicators.

Dynamic Obstacle Avoidance. This metric evaluates the algorithm’s on-line responsiveness and successful obstacle-avoidance in the scenario of a sudden or moving obstacle (situation) in the environment. This is important for the adoption of UAVs in realistic, non-idealised environments. A good dynamic obstacle avoidance algorithm should be able to dynamically sense a possible moving dynamic obstacle with prompt response and smoothly plan a new path in real-time to pass around it rather than demonstrating a sluggish or complete failure to the situation.

Sample efficiency. Sample efficency is measured in terms of the number of samples (i.e., time-steps) of interaction with the environment that an algorithm needs to achieve a desired level of performance (e.g., achieve a 90% success rate). Data collection is typically the most expensive step in a reinforcement learning setting in the real world. High sample effciency indicates that the algorithm requires fewer examples for learning, hence it could be trained with less training time and resources which is very critical for quick deployment and iteration.

Data Independence. This measure compares how much the algorithm relies on additional data, especially human expert demonstration data, for the learning process. Algorithms with high data independence (e.g. Q-Learning, A3C) could learn completely from scratch, i.e., by interacting alone with the environment. Meanwhile, an algorithm with low data dependence (e.g. Imitation Learning) always needs a dataset of good quality from the expert demonstration dataset. It reflects the degree of autonomous learning ability of the algorithm and the generalizability of the application scenarios of the algorithm.

4.2. Comprehensive performance comparison of RL algorithms in UAV path planning

On the intuitive dimension of path morphology, the evolutionary trend of different algorithms shows significant differences. Classical tabular methods (e.g., Q-Learning), due to their discrete state and action spaces, typically generate rigid, jagged paths(Fig. 1.). As illustrated in the figure, the Q-Learning algorithm navigates from a start point (green circle) to a target (blue star) within a 2D grid world, successfully maneuvering around several circular obstacles. The resulting path consists entirely of vertical and horizontal movements, creating a distinct "stair-step" trajectory. This demonstrates a key trend of the algorithm: while it finds a functional, collision-free route, the path is not smooth and often suboptimal in length, characterized by frequent, sharp 90-degree turns.

Although DQN can handle high-dimensional states, its discrete action output still leads to grid-like paths, presenting inherent limitations in smoothness and efficiency(Fig. 2.). The figure illustrates the typical trajectory generated by a DQN agent. As depicted in magenta, the path effectively connects the starting point and the target while maneuvering around obstacles. However, a notable pattern is that the trajectory is constrained to a grid-like structure, consisting exclusively of horizontal and vertical segments. This indicates that, despite the integration of a neural network, the algorithm's dependence on a discrete action space (e.g., up, down, left, right) leads to a jagged and non-smooth path, which is less efficient compared to a more direct and continuous trajectory.

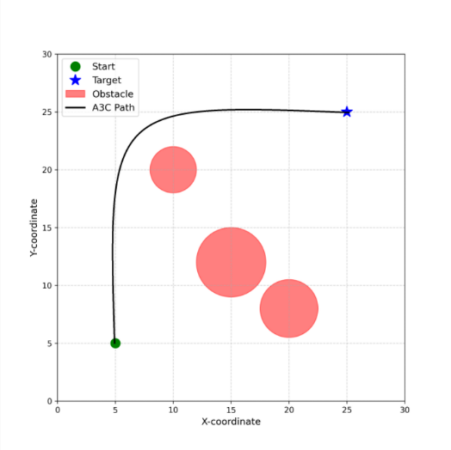
In contrast, policy-gradient algorithms like A3C/A2C can generate smooth and physically more feasible curved trajectories (Fig. 3.) by directly outputting continuous actions, demonstrating optimal performance in terms of path length and path smoothness. The figure clearly illustrates this trend, demonstrating that the A3C-generated path consists of a single, continuous curve connecting the start point to the target. The trajectory navigates through the environment with a sweeping motion, effectively avoiding the red obstacles without exhibiting jagged or abrupt turns. This characteristic of smoothness serves as a key indicator, highlighting the primary advantage of policy-gradient methods in this context: they generate trajectories that are not only more efficient in terms of path length but also more feasible for physical vehicles to execute in practice.

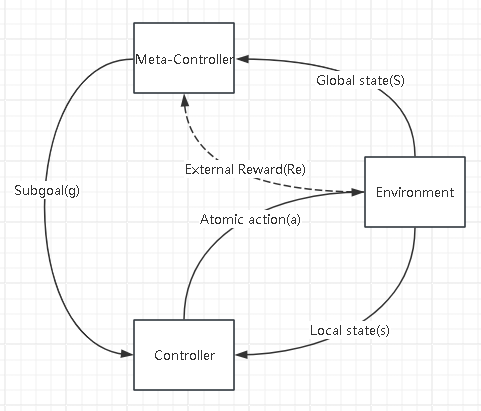
To solve more challenging application problems with different architectures, the advanced reinforcement learning techniques developed for solving large scale navigation tasks are specialized. Hierarchical Reinforcement Learning (HRL) aims to solve for the navigation problem with a long horizon. The hierarchical model in Fig. 4 illustrates its architecture. Our framework divides the decision making in two stages: a Meta-Controller(high-level policy) is in charge of macro planning, which takes in the global state (S) and outputs an abstract sub-goal (g); a Controller(low-level policy) is in charge of concrete execution, that takes in the local state (s) and receives the outputted sub-goal, and outputs a sequence of atomic actions (a). The whole learning is driven by the external reward (Re) from the environment.The chief strength of this task decomposition approach lies in its ability to address large and difficult problems.

Imitation Learning (IL) or Inverse Reinforcement Learning (IRL) offer an alternative answer for the problem, in which designing the reward function is challenging. Their process is illustrated in Fig. 5, which we call Expert Trajectory, given by a Human Expert. IL directly copies the expert to create a policy using supervised learning. While IRL uses the trajectories first to infer the reward function of the expert and applies it to regular RL. Because these techniques make direct use of efficient expert data, they are second to none with respect to the sample efficiency metric.

To make the multi-dimensional, comprehensive performance comparison, we draw a radar chart depicted in Fig. 6, where it visually demonstrates the comparison of performance profiles among all of the involved algorithms. We can clearly observe that A3C (black) has the most balanced and powerful performance in path smoothness, success rate, and dynamic adaptability, and DQN (magenta) has strong data independence, yet moderate performance and is an important research baseline for us. HRL (green) performs similarly in terms of path quality with A3C but has the lowest sample efficiency due to the high training cost that brings about strong planning ability. IL/IRL (blue) has high sample efficiency but it highly relies on expert data and poor generalization ability.

Lastly, there is no “optimal” algorithm that fits all. The choice of an algorithm for practical UAV path planning should depend on a trade-off of specifictask requirements: A3C is the best solution if fine control and high dynamic responsivenes are required; HRL is a promising solution for large scale, long horizon tasks; and IL/IRL is a special and effective route when reward engineering is hard and fast deployment is needed.

5. Challenges and future directions

5.1. Current challenges

While reinforcement learning has achieved a new breakthrough in the area of UAV path planning, applying the methods from simulation to physical world is still subject to a variety of difficulties.

The majority of deep RL algorithms including DQN and A3C, need a huge quantity of interaction data to obtain an efficient policy. For these algorithms, it is acceptable if learning can be done in simulation, but repeating millions of trial-anderror actions in real environment is not only time-consuming but also damaging to the UAV, making the cost beyond afford. This is the main bottleneck to suppress the practical usage of RL algorithms.

The majority of current research is conducted in idealized simulation environments. However, simulators can hardly perfectly model real-world factors such as complex physics dynamics, sensor noise, communication delays, and unpredictable airflows. Directly deploying a model trained in simulation onto a real UAV often results in a sharp decline in performance, or even complete failure.

The reward function plays a key role in the ultimate performance of the algorithm. A reward function designed without care will cause the agent to learn suboptimal, even potentially harmful, behaviors (e.g., taking a shortcut into an obstacle to maximize a distance-based reward). For complicated missions, manually crafting the perfect reward function which encompasses everything that may happen, is in effect impossible.

Policy networks based on deep learning are often regarded as ”black boxes”, whose decision-making process is not easy to explain. It is unacceptable when a model cannot justify the decision-making results in safetycritical applications such as UAV flight. To make the policy safe to work in all and especially extreme conditions is the main difficulty of current studies.

5.2. Future directions

As discussed above, to meet with the key issues, there are several research areas that should be of concern for future research to balance the two essential indexes of safety and sample efficiency on UAV path planning.

More work needs to be done on how to integrate Imitation learning (IL) with on-line RL. We can pre-train an agent in an IL based approach using a limited set of expert demonstrations to obtain an initial learned policy to be further tuned and optimized in the environment via on-line interactions. Meta-Learning as well as Offline RL hold additional possible avenues to take advantage of available datasets to fast adapt to new tasks.

Domain Adaptation and Domain Randomization are viable solutions to the Sim-to-Real issue. Injecting various noise and randomizing some parameters (such as changing the mass of UAVs, the efficiency of the motors, and wind force) in the simulation when training the model, helps the model be forced to learn a policy more robust to the environmental variations so as to enhance the generalization ability of the real world.

Despite providing a natural starting point for automatically learning reward function, Inverse Reinforcement Learning (IRL) is known to have high computational complexity. A more interesting route is to search for reward terms rooted in intrinsic curiosity, which rewards the agent by not just achieving the task but also exploring new states, providing a reward to encourage thorough exploration (potentially to discover a better policy).

As a solution to the “black box” problem, one can incorporate Constrained RL that explicitly uses safety constraints (i.e., “must avoid obstacles at a minimum range”) in the training to endow the resultant policy with the safety at the very beginning. Simultaneously, we should also leverage explainable AI (XAI) methods (e.g., attention visualization) to enable understanding why a specific conclusion was reached; hence, it is aimed to enhance future UAV system reliability.

6. Conclusion

In this paper, we have systematically studied the adoption of RL in the autonomous path planning field of UAVs. We first described how to abstract the complex physical path planning problem into a traditional MDP and derived the theoretical background for adoption of RL algorithms. Second, in this paper, we presented an overview of various algorithms from the original Q-Learning, DQN algorithm to recent research, including A3C, HRL, and IL algorithms, discussing the basic concepts and the target application.

By multiple comprehensive comparisons, we elucidate the important balance among these three kinds of algorithms. The result shows policy gradient algorithms, such as A3C are more competitive for producing continuous dynamics and smooth trajectories due to their capability for dealing with continuous action space. HRL provides a practical solution to such large scale, long-horizon navigation problems by task decomposition. And IL proves to be with good learning efficiency in situations that reward function engineering becomes complicated.

Despite open problems in sample efficiency, sim-to-real transfer, safety, etc., the research of RL undoubtedly opens the most potential technological avenue to develop truly automatic UAV navigation systems that equip UAVs with the ability to learn the optimal strategies autonomously through learning and interacting with unknown and dynamic environments, in turn circumventing the need of having precise environment models. The future work, while concentrating on sample efficiency improvement and decision safe-guaranteed will surely give a better direction to the practical implementation of RL in the UAV field, i.e., the intelligent, reliable and efficient autonomous flying UAV systems. In summary, RL is not just an efficient optimizer for the ongoing path planning algorithm but will also be a fundamental agent driving the future of UAV intelligent.