1. Introduction

The global automotive fleet has expanded steadily alongside economic growth, reaching 1.474 billion vehicles by 2023. Regional distribution data reveals Asia as the dominant market with 543 million vehicles, followed by Europe (413 million) and North America (358 million). China’s position as a leading automotive nation is underscored by International Energy Agency reports documenting its unprecedented vehicular oil consumption over the past three decades, with aggregate thermal energy expenditure approximating 446,054,810 billion joules between 1990-2021 [1]. Aerodynamic refinement has emerged as a pragmatically great pathway to this challenge, as evidenced by industry benchmarks like the Xiaomi SU7’s 0.195 drag coefficient at 160 km/h and BMW’s 0.23 drag coefficient for the 2024 3 Series at 120 km/h [2]. Within this context, roof vortex generators represent an understudied yet impactful aerodynamic element. Empirical evidence suggests properly configured vortex generators can reduce high-speed fuel consumption by approximately 3%, presenting a meaningful opportunity for fleet-wide energy savings. This investigation therefore focuses on developing a systematic biomimetic design methodology for vortex generators applied to three-box sedan architectures—the prevailing market segment—with the objective of maximizing aerodynamic efficiency.

Prior research has established foundational principles for vortex generator applications. Md. Rasedul Islam’s aircraft-derived studies demonstrated the efficacy of vortex generation in delaying roof airflow separation [3], while Mohan Jagadeesh Kumar quantified optimal vortex generator dimensions relative to boundary layer thickness (15-25mm) [4]. The collective work of L. Anantha Raman [5] and Zulfaa Mohammed-Kassim [6] has further validated drag reduction strategies across vehicle classes. Recent investigations have revealed critical design trade-offs: Xinkai Li’s work correlated vortex generator height with both enhanced flow control and increased parasitic drag [7], whereas Muhammad Pirdaus Ismail established the drag-reducing effects of greater vortex generator density and reduced fillet radii [8]. Biomimetic approaches have shown particular promise, beginning with Oeffner’s shark skin derivations [9] and culminating in August Domel’s microstructured vortex generators for aviation applications [10]. Most recently, Zhaohuang Zhang’s manta ray-inspired designs have demonstrated superior performance to conventional triangular profiles [11].

This study synthesizes existing vortex generator knowledge with novel biomimetic principles through computational fluid dynamics analysis. Three biologically inspired vortex generator configurations are evaluated on a representative sedan platform to establish quantitative performance benchmarks. The investigation addresses three critical gaps in current scholarship: the absence of systematic roof vortex generator design methodologies, historical limitations in computational fluid dynamics fidelity, and the untapped potential of biomimetic design principles in automotive applications. Methodological constraints include the singular vehicle platform analyzed and the absence of wind tunnel validation—limitations that nevertheless do not diminish the study’s significance as pioneering work in this specialized domain. Subsequent sections will detail the research methodology, present comparative results of the three biomimetic designs, discuss optimization pathways based on vortex development characteristics, and conclude with recommendations for future research directions.

2. Methodology

In this study, computational fluid dynamics (CFD) software plays a central role in simulating turbulent flows over airfoils and vehicles. At the heart of these simulations are the governing equations, which are essential for accurately capturing fluid behavior. The first of these is the mass conservation equation [12]:

$$ \frac{\text{∂}{\text{u}}_{\text{i}}}{\text{∂}{\text{x}}_{\text{i}}}\text{=0}$$(1)

This equation ensures that mass is conserved within the flow domain—it states that any net increase in mass within a control volume must be balanced by an equivalent net mass flux across its boundaries. This fundamental principle guarantees that the simulation remains physically consistent, with no artificial gain or loss of mass. The second set of governing equations comprises the Navier–Stokes equations, which describe the conservation of momentum. These equations are a mathematical representation of Newton's second law applied to fluid motion. They account for fluid inertia, pressure gradients, viscous effects, and external forces, providing a comprehensive framework for modeling the complex behavior of turbulent flows. In index notation, the momentum equations in the streamwise, spanwise, and wall-normal directions are expressed as [12]:

$$ \frac{\text{∂}{\text{u}}_{\text{i}}}{\text{∂}\text{t}}\text{+}{\text{u}}_{\text{j}}\frac{\text{∂}{\text{u}}_{\text{i}}}{\text{∂}{\text{x}}_{\text{j}}}\text{=−}\frac{\text{1}}{\text{ρ}}\frac{\text{∂}\text{p}}{\text{∂}{\text{x}}_{\text{i}}}\text{+}\left(\text{ν}\text{+}{\text{ν}}_{\text{T}}\right)\frac{{\text{∂}}^{\text{2}}{\text{u}}_{\text{i}}}{\text{∂}{{\text{x}}_{\text{j}}}^{\text{2}}}\text{+}{\text{F}}_{\text{i}}$$(2)

Here,  $$ {\text{u}}_{\text{i}}\text{=(u,v,w)}$$  is the velocity components in three directions,  $$ \text{p}$$  is the pressure,  $$ \text{ν=μ/ρ}$$  is the kinematic viscosity,  $$ {\text{ν}}_{\text{T}}$$  is the turbulent viscosity which is determined by turbulent model,  $$ \text{ρ}$$  is the density of the air, and  $$ {\text{F}}_{\text{i}}$$  is the forces from the car to the flow fields, including the drag and lift forces. To quantify the aerodynamic performance of a vehicle, the drag coefficient is used as for analysis. The drag coefficient, Cd ​, which measures resistance to motion through the fluid, is defined as [12]:

$$ {\text{C}}_{\text{d}}\text{=}\frac{\text{2}\text{D}}{\text{ρ}{\text{u}}_{\text{1}}^{\text{2}}\text{A}}$$(3)

where D is the drag force exerted on the car, u​ is the freestream (streamwise) velocity, and A is the frontal area of the car. A lower drag coefficient indicates reduced aerodynamic resistance and improved efficiency. This research utilizes SolidWorks 2024 for both geometric modeling and CFD simulation. SolidWorks is a widely adopted engineering software platform known for its versatility in mechanical design, product development, and fluid analysis.

3. Results and discussion

3.1. Model development

To investigate the aerodynamic effects of vortex generators, this study developed a detailed vehicle model and integrated a series of biomimetic vortex generator designs. A fastback sedan-style vehicle was selected as the baseline geometry due to its sensitivity to flow separation, making it an ideal platform for demonstrating the effectiveness of vortex control strategies. The model was dimensioned based on the Mercedes-Benz EQS, a representative fastback vehicle, with an overall length of approximately 5.2 meters, a width of 2.1 meters, and a height of 1.5 meters. To improve computational efficiency and focus the analysis on aerodynamic behavior, minor surface details were omitted during the modeling process.

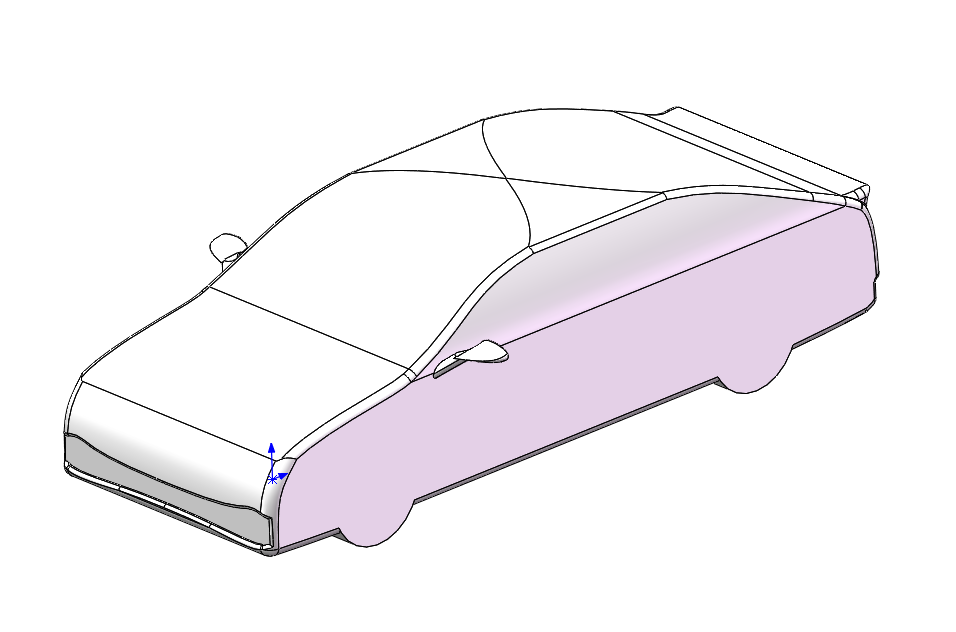
Three distinct vortex generators were developed, each inspired by natural geometries known for their effective interaction with fluid flows. The first design emulated the curvature of a shark’s dorsal fin, the second was modeled after the streamlined profile of a stingray’s body, and the third replicated the micro-grooved texture characteristic of shark skin. To ensure a consistent and controlled comparison, all vortex generators were positioned identically on the vehicle surface and designed with the same projected area.

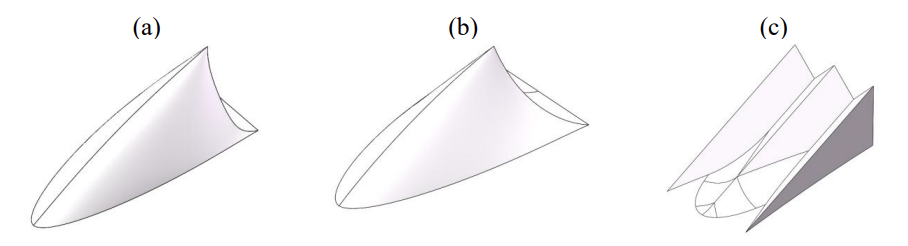
3.2. Aerodynamic performance of the three biomimetic vortex generators

In the following section, we compare the drag coefficient (Cd, calculated using Equation (3)) and simulation results for the vehicle equipped with each of the three vortex generator designs. The analysis focuses on three key flow parameters: velocity, static pressure, and local velocity vectors. To facilitate a clear comparison, cross-sectional views along the side of the vehicle are used to visualize and evaluate the aerodynamic effects of each vortex generator configuration.

Figure 3. shows the drag coefficient of the car with three different vortex generators designs. The Cd corresponding to the three vortex generator designs are 0.1883, 0.1882, and 0.1845, respectively. Design 3 has the best aerodynamic effect while the other two are equally the same.

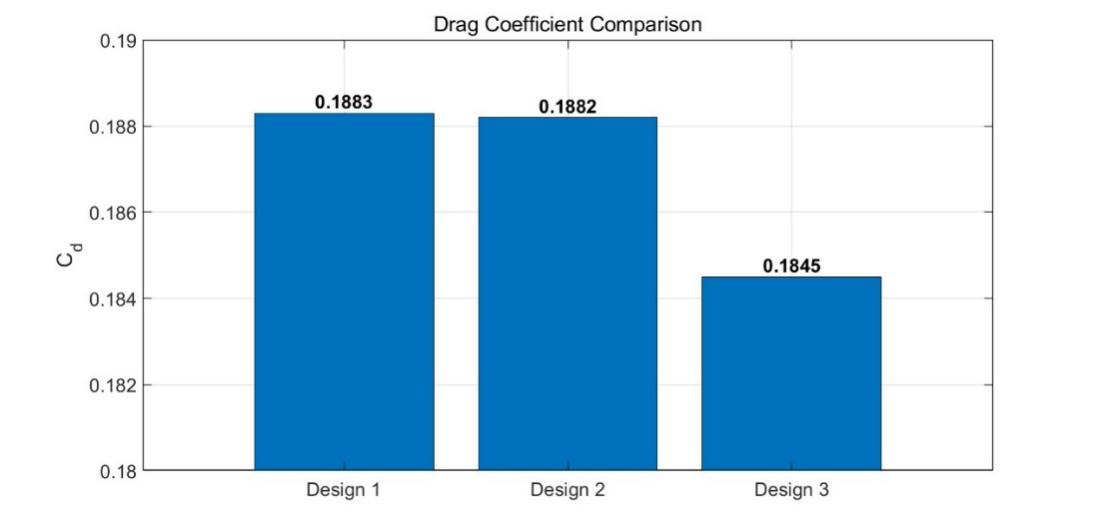
Figure 4 presents the airflow velocity results for the car equipped with three different vortex generators. Two key features are evident across all designs: (1) large low-speed zones appear in front of and behind the car, along with a smaller low-speed zone near the lower A-pillar—both unavoidable during high-speed driving; and (2) high-speed zones dominate the car’s roof and the area below the front bumper. However, the focus of this analysis lies in the differences introduced by the vortex generator designs. Notably, the shark skin-inspired vortex generator (Design 3) exhibits a significantly larger low-speed zone behind it compared to the other two designs. Additionally, the high-speed zone atop Design 3 is smaller than those observed in the alternative configurations.

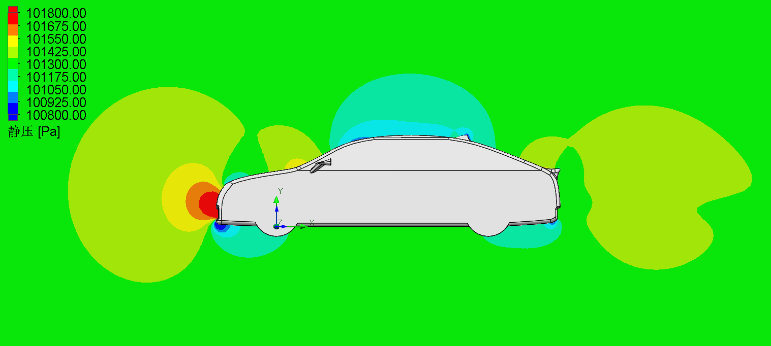
Figure 5 presents the static pressure simulation results for the car equipped with three different vortex generators, revealing two consistent trends: a large high-pressure zone at the front and a smaller one above the tail, alongside distinct low-pressure zones beneath both bumpers and atop the car. The stingray-inspired design (Design 2) exhibits the smallest rear low-pressure zone, while the shark skin-inspired design (Design 3) generates the largest rear low-pressure zone due to vortex effects—with its lowest-pressure region positioned farthest from the generator body and the highest pressure occurring directly adjacent to its rear surface. Additionally, Design 3 produces a slightly smaller fastback low-pressure zone compared to the other two designs.

(a)
(b)
(c)

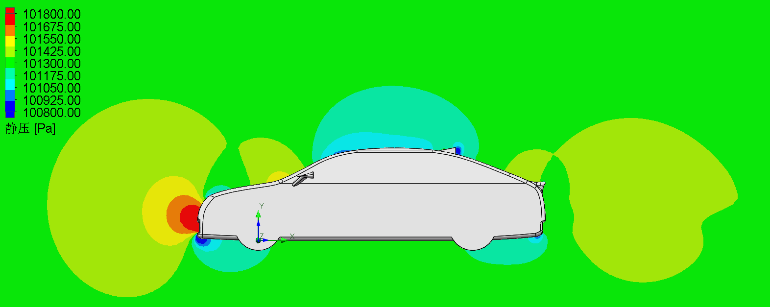Figure 5. Static pressure at the cross-section of the car, (a) Design 1, (b) Design 2, (c) Design 3.

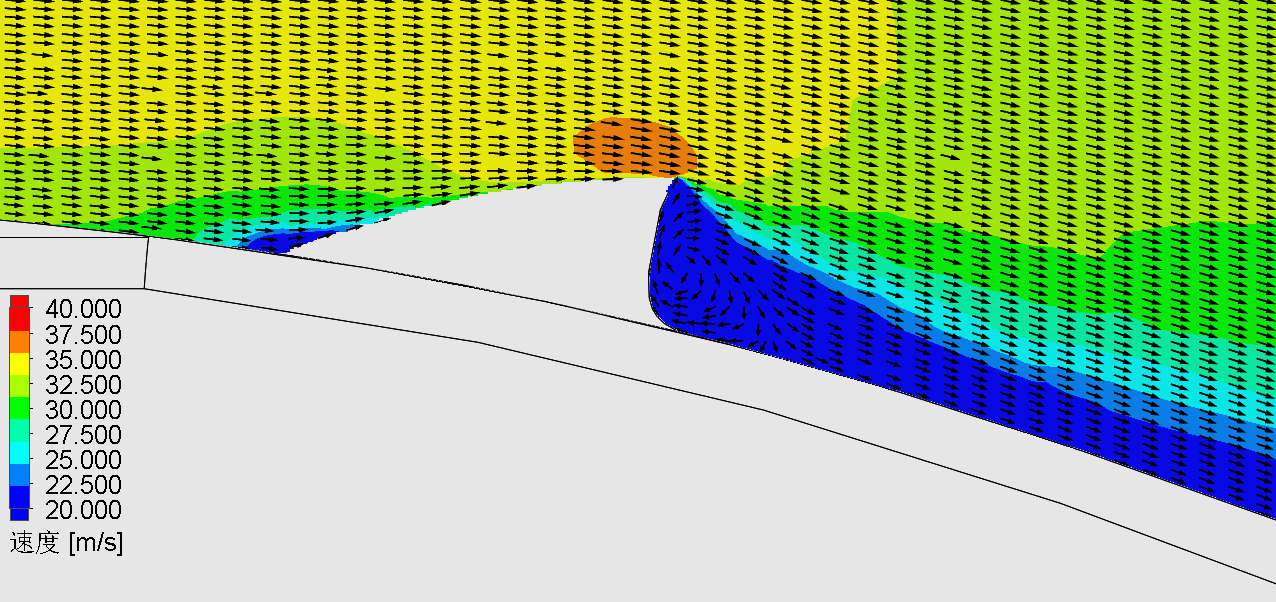
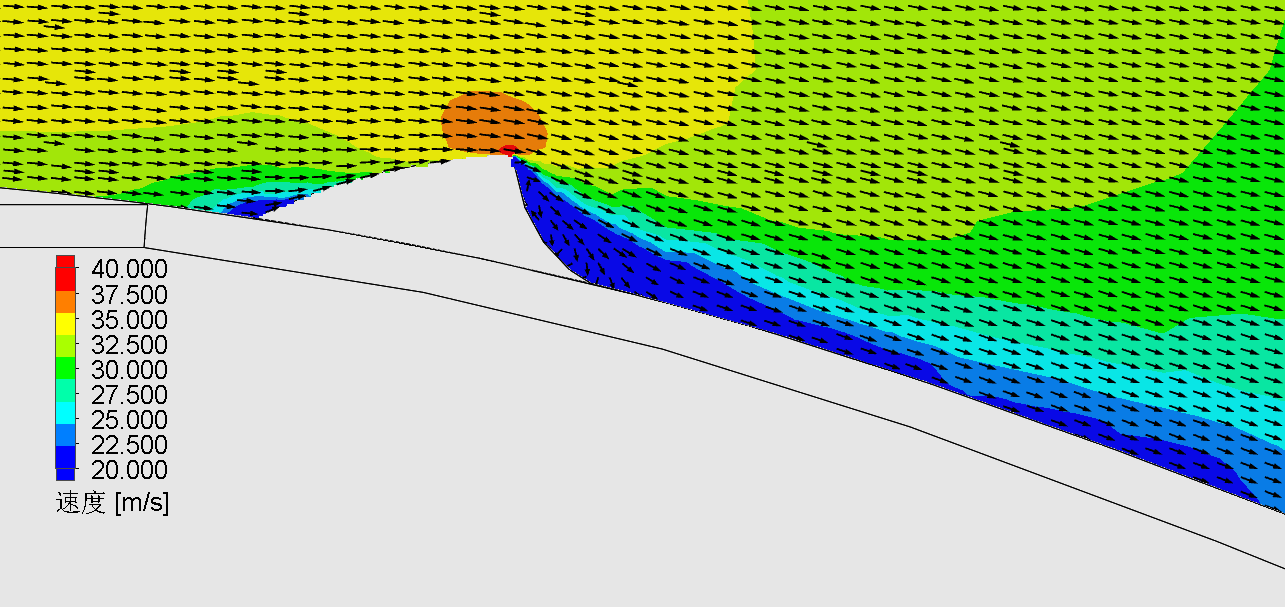
To clearly illustrate the vortex structures generated by each design, we further analyze the local velocity vectors in the vicinity of the vortex generators. Figure 6 presents the results of local flow fields for the vehicle equipped with the three different vortex generators. While all three designs successfully generate vortices, the vortex generator inspired by the core structure of shark skin (Design 3) produces the most well-developed and coherent vortex. This indicates superior performance in suppressing flow separation and reducing aerodynamic drag. In contrast, the design based on the stingray’s body curvature (Design 2) yields the weakest and least organized vortex structure, suggesting a comparatively lower effectiveness in enhancing aerodynamic performance.

(a)
(b)
(c)

Figure 6. Local velocity vectors near the vortex generator at the cross-section of the car, (a) Design 1, (b) Design 2, (c) Design 3

3.3. Optimization of shark-skin inspired design (design 3)

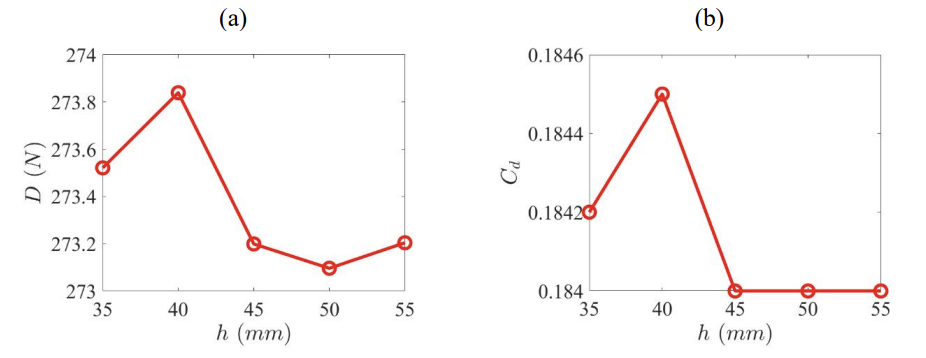
To further optimize the vortex generator with the best aerodynamic performance identified earlier, we evaluated five variants of the shark skin-inspired design (Design 3) with groove depths of 35 mm, 40 mm, 45 mm, 50 mm, and 55 mm. The comparison was based on drag force, drag coefficient (Cd, calculated using Equation (3)), and CFD simulations analyzing velocity fields, static pressure distributions, and local velocity vectors. Cross-sectional side views of the car were used for the CFD analysis.

Figure 7 presents the drag forces and corresponding Cd values for the five designs. The measured drag forces are 273.521 N, 273.839 N, 273.199 N, 273.096 N, and 273.204 N, respectively, while the Cd values are 0.1842, 0.1845, 0.1840, 0.1840, and 0.1840. Although the latter three designs yielded identical Cd values to four significant figures, the 50 mm groove depth produced the lowest drag (273.096 N), confirming its status as the optimal configuration.

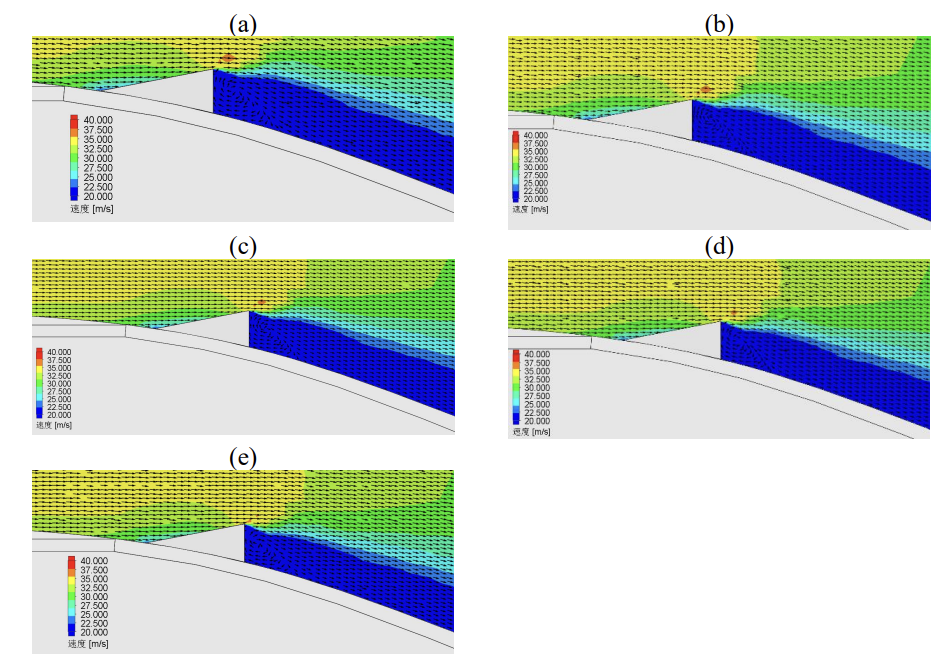
To clearly visualize the vortex behavior, we further analyzed the local velocity vectors near the vortex generator. Figure 10 presents the results of these velocity vectors for the car equipped with vortex generators of varying groove depths. The comparison in Figure 10 confirms that when the groove depth is 50 mm, the vortex exhibits the highest integrity and uniformity, as evidenced by the relatively consistent airflow density across different positions within the vortex. Additionally, the vortex's shape and position are optimally configured to minimize airflow separation, resulting in the lowest drag among all tested configurations.

4. Conclusion and future work

This study employed computational fluid dynamics (CFD) to evaluate the aerodynamic performance of three biomimetic roof vortex generators: a shark dorsal fin-inspired design, a stingray body curve-inspired design, and a shark skin core structure-inspired design. The results demonstrated that the shark skin-inspired vortex generator, despite being less commonly implemented in practice, outperformed the more conventional designs, achieving a maximum drag coefficient reduction of 0.0043. Subsequent optimization of groove depth revealed that a 50 mm configuration delivered optimal aerodynamic performance within the tested range (35-55 mm). While this research has provided promising results, several areas warrant further investigation. First, the unexpected peak in drag observed at the 40 mm groove depth requires more detailed quantitative analysis to explain the underlying fluid dynamics. Second, the current CFD-based findings should be validated through wind tunnel experiments to confirm their real-world applicability. Future work will address these limitations while exploring additional geometric parameters and their effects on aerodynamic performance.