1. Introduction

The connected subgraph of a connected graph with the fewest edges, which must include all of the connected graph's nodes, is called the spanning tree [1]. Additionally, a well-known optimization issue in graph theory is the minimal spanning tree (MST) problem. Given an undirected, weighted graph, the goal of the MST problem is to find a tree that spans all the vertices of the graph with the minimum possible total edge weight. Moreover, it has much realistic meaning. MST is widely used in many fields [2-4]. For instance, in network design, a minimum spanning tree can help to optimize the layout of a network, which is found to be helpful in designing the transportation system in urban and rural areas. Next, this article will cover three algorithms (Kruskal, Prim, and Boruvka) that can solve this problem, showing the very steps of the algorithms in detail [5-7]. Then, by using the method of comparison, the differences and commonalities can be found. Lastly, specific backgrounds for applying these three algorithms will be shown.

2. Kruskal’s algorithm

2.1. Specific steps

Sort all the edges in an ascending order of weight;

Start a loop starting with the edge of the least weight;

For each edge:

If adding it to the current MST won’t create a cycle;

Then add it to the MST;

If n-1 edges have been added, then stop the loop;

(n is the amount of the nodes).

2.2. Applying Kruskal’s algorithm in a specific graph

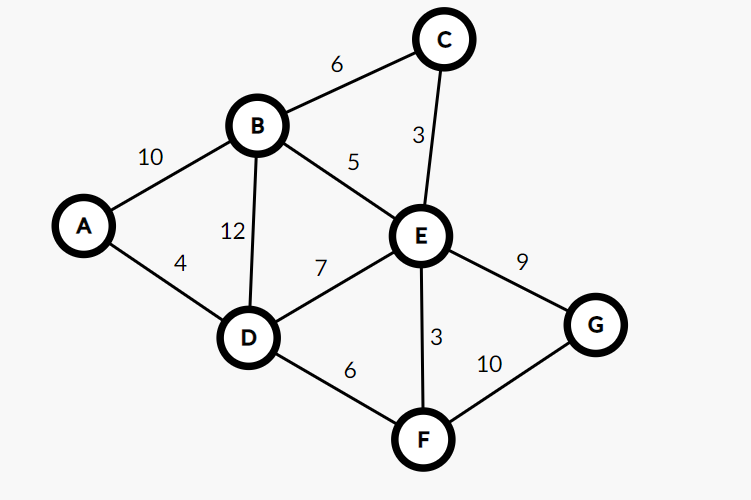
Figure 1. A sample weighted and undirected graph.

Here are the steps of applying Kruskal’s algorithm in the undirected graph above.

The edge with the least weight is CE, and adding it won’t create a cycle. Add CE to the MST.

Next one is EF, and adding it won’t create a cycle. Add EF to the MST.

Next one is AD, and adding it won’t create a cycle. Add AD to the MST.

Next one is BE, and adding it won’t create a cycle. Add BE to the MST.

Next one is DF, and adding it won’t create a cycle. Add DF to the MST.

Next one is BC, and adding it will create a cycle (BC-BE-CE). So, skip BC.

Next one is DE, and adding it will create a cycle (DE-EF-DF). So, skip DE.

Next one is EG, and adding it won’t create a cycle. Add EG to the MST.

Up to now, 6 edges have already been added to the MST. Since there are 7 vertices in the graph, the MST has already been created.

2.3. A universal method to determine whether a cycle will be created

2.3.1. The union-find algorithm. The disjoint-set data structure, sometimes referred to as the union-find algorithm, is a group of techniques that enables us to effectively manage a collection of disjoint sets. Union and find are the union-find algorithm's primary operations.

The find operation takes an element as input and returns the unique identifier of the set that the element belongs to. If two elements have the same unique identifier, then they belong to the same set. Usually, recursion will be applied in this operation.

The union operation takes two sets and merges them into a single set. This operation is accomplished by assigning the identifier of one set to the other merged set.

In terms of a tree, the set is a subtree, and the unique identifier is the root node. The find operation recursively follows the parent node of a node until the root node is found.

2.3.2. The application of the union-find algorithm in this process. For each edge, tell whether its two nodes have the same root node (identifier) with the find operation. If so, it means that the two nodes are already in the same tree. As a result, connecting them with this edge will create a cycle. Consequently, if the two nodes are not in the same tree, then join the edge into the MST and set the one node’s root node to the other node’s root node to join this node to the MST, which is called the union operation.

2.4. Time complexity analysis

The whole algorithm contains two main parts: the sorting and the loop of the edges. Obviously, the time complexity of the latter one is O(n) (n is the number of the nodes) which is absolutely less than the sorting operation. The complexity of the sorting algorithm can reach as low as O (nlogn) by applying quick sort, merge sort, etc. So, the final time complexity is the larger one, O (nlogn).

3. Prim’s algorithm

3.1. Specific steps

Choose a random node as the starting node.

Create a set (named S) of nodes that are not yet in the MST. Initially, this set contains all nodes except the starting node.

For each node in the MST, find the cheapest edge that connects it to a node in S.

Select this node with the cheapest edge and add it to the MST, and remove this node from S.

Repeat steps 3 and 4 until all nodes are in the MST.

3.2. Applying Prim’s algorithm in a specific graph

Figure 2. A sample weighted and undirected graph.

Here are the steps of applying Prim’s algorithm in the undirected graph above.

Choose A as the starting node. The set of nodes that are not in the MST yet is S, which contains B, C, D, E, F, and G now.

The cheapest edge connecting MST and S is AD weighted 5, so add AD to MST and remove D from S. The present S is B, C, E, F, and G.

The cheapest edge connecting MST and S is DF weighted 6, so add DF to MST and remove F from S. The present S is B, C, E, and G.

The cheapest edge connecting MST and S is AB weighted 7, so add AB to MST and remove B from S. The present S is C, E, and G.

The cheapest edge connecting MST and S is BC weighted 8, so add BC to MST and remove C from S. The present S is E, and G.

The cheapest edge connecting MST and S is CE weighted 5, so add CE to MST and remove E from S. The present S is G.

The cheapest edge connecting MST and G is EG weighted 9, so add EG to MST and remove G from S. The present S is empty. The algorithm ends.

3.3. Time Complexity analysis

The time complexity of Prim's algorithm is O (n ^ 2), where n is the number of nodes in the graph. However, if a priority queue is used to select the minimum-weight edge at each step, it takes O (log n) time to extract the minimum element. The algorithm repeats this process m-1 times to construct the MST. In conclusion, the total time complexity of the algorithm is O (m log n). (m is the number of edges in the graph.)

4. Boruvka’s algorithm

4.1. Main ideas

Boruvka’s algorithm can be considered as the combination of Prim and Kruskal [8].

For each current connected block, find the shortest edge from this connected block that is not in the minimum spanning tree and reaches other connected blocks.

Add it to the MST.

Repeat this process until the MST is built.

4.2. Specific steps

As we get started, every single node is considered as a connected component itself. We will start the process with them.

Firstly, find the cheapest edge leaving a component by checking all the edges. If one edge meets these restrictions, it has not been used yet, so merging it is not going to create a cycle.

Then find the root node of the tree to which one terminal node belongs, check if the current edge is cheaper than its current cheapest edge. If so, update it. Then do the same thing to the other terminal node of this edge.

After a loop, the cheapest edges of each component can be obtained.

Check all the nodes to merge each cheapest edge if it hasn’t been used before. Once an edge is merged, mark it as used and use the union operation to merge one component with the other.

Repeat the whole process until n-1 edges are merged.

4.3. Applying Boruvka’s algorithm in a specific graph

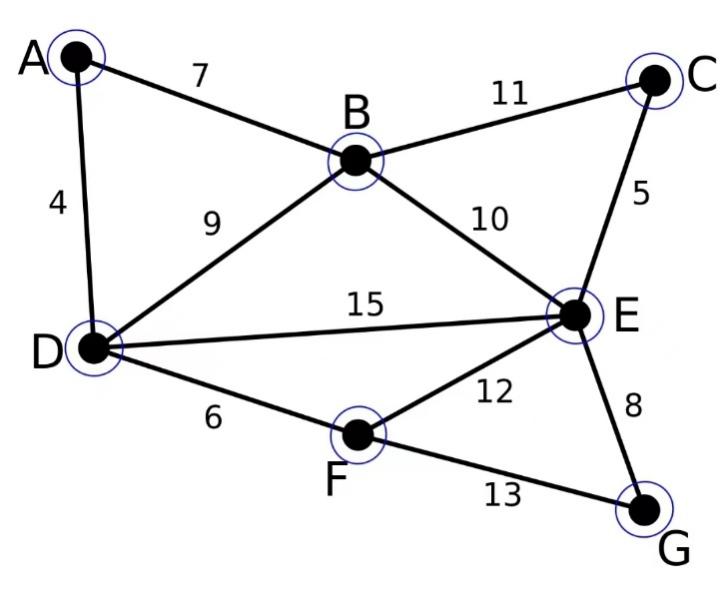
Figure 3. A sample weighted and undirected graph.

Initially, all the nodes are considered as a single component.

Loop all the edges and find the “Best” array.

AB is best for B;

AD is best for A and D;

DF is best for F;

EG is best for G;

CD is best for C and E.

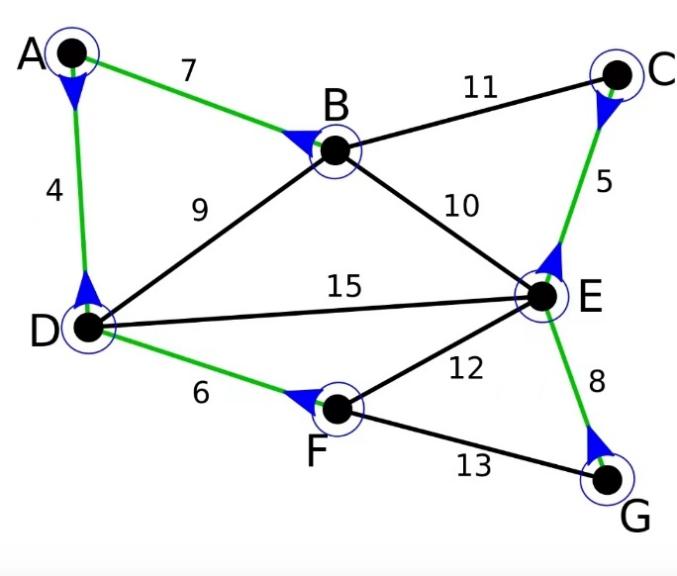
Figure 4. Every “Best” edges are obtained.

Then merge all the connected nodes to a bigger component.

Figure 5. Finding the cheapest edge connecting two blocks.

Loop all the edges and find the “Best” array.

In the all-available edges, BE is the cheapest to connect the two components. Add it to the MST.

Up to now, n-1 edges have been merged, so the MST has been built.

4.4. The application of the union-find algorithm in this process

In Boruvka's algorithm, each node initially belongs to a separate set (tree). During each iteration, the algorithm scans all the edges in the graph and, for each component, finds the cheapest edge that connects it to a node not in the component. To do this efficiently, the algorithm uses the Find operation to determine which component a node belongs to. If two nodes are connected by an edge, the Union operation is used to merge the components containing the two vertices.

The algorithm repeats this process until there is only one component left, which corresponds to the MST. The use of the union-find algorithm allows the algorithm to efficiently determine the components that each node belongs to and to merge components when necessary.

4.5. Time complexity analysis

N nodes need to be merged for log n times; every merging operation is O(m) because every edge needs to be checked to maintain the cheapest edge of each component. So, the total time complexity is O (m log n).

5. The comparison of the three algorithms

Obviously, these three algorithms can reach the same goal with different time complexity. So, it’s necessary to make a judgement about which one should be applied. By observing the formula of each one, the Kruskal's algorithm has a time complexity of O(m log m), where m is the number of edges in the graph, making it appropriate for determining the MST of a sparse graph [9]. Regardless matter how many edges are there in a graph, the Prim method has an O(n^2) computational cost. To determine the MST of a dense graph, the Prim's technique is therefore appropriate [10]. Prim’s algorithm is still outstanding in dense graphs since its time complexity is O (m log n) with the optimizing of priority queue. Boruvka’s algorithm is the same as Prim’s algorithm in terms of time complexity.

Here is the experiment:

Separately generate three sparse graphs randomly, run these three algorithms to find the MST for 1000 times. Then calculate the average runtime.

Table 1. The average runtime of the three algorithms in an example sparse graph.

As the Table 1 shows, Kruskal is much better.

Separately generate three dense graphs randomly, run these three algorithms to find the MST for 1000 times. Then calculate the average runtime.

Table 2. The average runtime of the three algorithms in an example dense graph.

As the Table 2 shows, Prim and Boruvka are better.

6. Conclusion

This paper elaborated the main ideas and implementation steps of three typical MST algorithms and analyzed their time complexity. It also introduced an important algorithm called union-find algorithm and its application in Kruskal’s and Boruvka’s algorithm. In the end, the differences of three algorithms are discussed, indicating their suitable situation. However, it doesn’t talk about the various optimization methods of these algorithms which can result in different time complexity in the end. In the future research, multiple optimization methods of these three algorithms will be taken into consideration and the difference of their efficiency will be also discussed.