1. Introduction

Robotics and autonomous systems have made incredible strides these years, transforming many different industries and facets of daily life. The rapid progress in artificial intelligence, computer vision, and sensor technologies has been the driving force behind the remarkable achievements in robotics and unmanned vehicles.

In the realm of robotics, researchers and engineers have focused on developing versatile and adaptable robots capable of assisting humans in a multitude of tasks. From collaborative robots (cobots) working alongside human operators in manufacturing and assembly lines to sophisticated robotic prosthetics enabling enhanced mobility for individuals with disabilities, the applications are diverse and impactful.

The rise of autonomous vehicles and the pursuit of fully self-driving cars have also captured significant attention in the last decade. Advancements in sensor fusion, machine learning algorithms, and high-definition mapping have propelled the development of autonomous driving technology. Companies and research institutions worldwide are investing vast resources into testing and refining self-driving cars to ensure their safety and reliability.

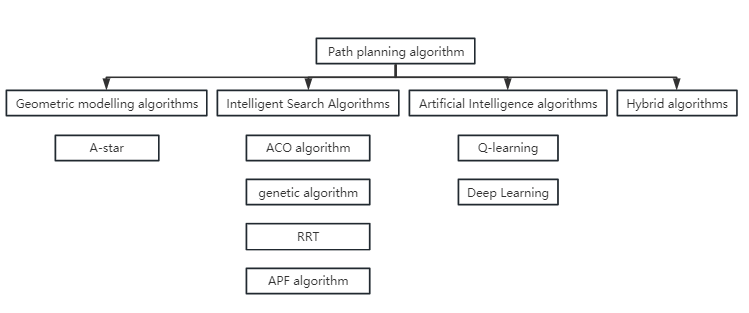
However, neither robotics nor driverless technology can be separated from the core technology of path planning. One of the most crucial elements of robotics and automation, path planning is utilized in mechanical device trajectory planning, driverless vehicle technology, automated navigation, and many other areas. Efficient and good path planning has a crucial impact on the working capacity and efficiency of various devices. This paper will introduce some common and frequently used algorithms one by one in four parts, as shown in Fig. 1, which are divided into geometric search algorithms, intelligent search algorithms, artificial intelligence algorithms, and hybrid algorithms for introduction.

2. Geometric modelling algorithm

The emergence of geometric modelling algorithms can be traced back to a relatively early period, and they usually started to be widely studied and applied in the 1980s and 1990s. These algorithms plan paths based on the geometric information of the environment, and they demonstrate a high degree of accuracy in path planning for static environments.

3. A-star algorithm(A* )

A* algorithm is a classic heuristic path search algorithm, commonly used in artificial intelligence.A* algorithm in most cases can efficiently find the optimal path between two points, but its efficiency in different constraints will have a big difference, a appropriate set of constraints will directly increase the algorithm's effectiveness.

The core of the A* algorithm lies in the design of the estimation function, as shown in the following equation: f(x)=g(x)+h(x), where f(x) indicates the total estimated cost from the start to the target node by means of node x while g(x) refers to the dissipation function, corresponding to the actual cost from start to node "x"; h(x) denotes the heuristic function, which stands for the estimated cost of node x to the end. The heuristic function is the core of the A-star, and is widely used as the "Manhattan distance" or the "Euclidean distance". This is widely used in many related fields due to its high computational speed and accuracy, but due to the small number of factors considered in the computation process, the paths are often not smooth enough or duplicate paths occur.

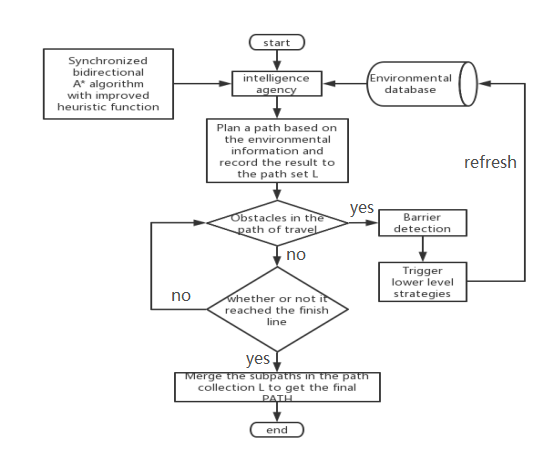
WanRu Du et al. proposed a multilayer bidirectional A-star, which introduces a layered strategy as shown in Fig. 2 to enable the robot to respond to sudden obstacles in real time during travelling and perform effective obstacle avoidance path planning [1]. The algorithm simultaneously changes to bi-directional search to simplify the algorithm and enhances the heuristic cost function to hasten convergence towards the selected node, increasing the algorithm's effectiveness for path planning in massive environments.

Figure 2. Improved multilayer bi-directional A* algorithmic framework [1].

4. Intelligent search algorithm

Intelligent search algorithms are an important class of methods in path planning algorithms whose emergence dates back to the 1990s. This class of algorithms is characterised by the use of heuristic information and intelligent search strategies to help robots or unmanned systems find efficient paths.

5. Ant colony algorithm

The ACO algorithm was first proposed by Italian scholars Colorni A., Dorigo M. in 1991.[2] This algorithm is based on how ants forage in the natural world and by simulating the ant colony and the pheromones released in the way, it is able to plan a better route by the concentration of pheromones in different areas within a certain period of time. The ACO algorithm can adjust the search range of the path and the method's rate of convergence by altering the pheromone inspiring factor and the random value, and the subsequent optimisation algorithms such as the elite ACO algorithm or the hierarchical ACO algorithm are more adjusted and improved in terms of the parameters of the algorithm itself [3].The algorithm is highly applicable and efficient, but it suffers from shortcomings such as initial blind search due to over-reliance on pheromones, slow convergence of the algorithm, as well as the tendency to fall into local optimisation.

To address the robot path planning issue with regard to these flaws, Zhibo Zhai et al. suggested an ant colony method that utilized the combination of Laplace distribution and dynamic window [4]. The new one improves the traditional ant colony algorithm mainly through two aspects. Firstly, the information about the current, next and target node is added into the heuristic information, and a new dynamic adjustment factor is added, so that the heuristic information and the pheromone mainly guide the algorithm in the early and late iterations, respectively; Secondly, the Laplace distribution is added to the pheromone to control the pheromone's escape, speeding up the algorithm's convergence rate. Then, the path generated by ACO is removed due to the bi-directional redundant nodes, improving the path's smoothness. Finally, the improved ACO and dynamic window algorithm are integrated to complete the path planning.

6. Genetic algorithm

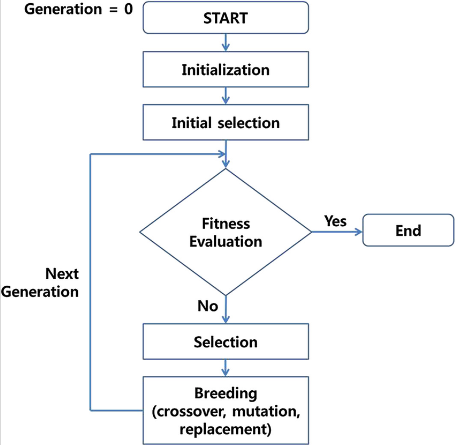
A group of search algorithms called genetic algorithms were developed in response to the hypothesis that there is natural development, which is first proposed by John H. Holland [5]. The theoretically optimal genetic material is obtained by mimicking the eugenics of reproduction and selection in the natural environment. The algorithm allows the solutions of each node to be exchanged, copied, eliminated or mutated to obtain the optimal solution. Individuals are assessed using a fitness function at each iteration of the algorithm; those with greater fitness values reflect superior solutions, which have a greater probability to be picked for reproduction and whose qualities will be displayed in the following generation. The fitness value of the solution rises while the genetic algorithm runs, and so does its quality, until a solution that satisfies the final criteria is found, at which point the method is terminated. The principle of the algorithm is shown in Fig. 3.

Figure 3. An illustration showing the genetic algorithm's foundation.

An improved adaptive genetic path planning method was proposed by Junfu Song et al. [6]. The adaptive function is made to plan paths more efficiently in the algorithm by introducing a turning angle evaluation index. Meanwhile, the inclusion of catastrophe operation and reversal operation optimises the adaptive adjustment method of crossover probability and mutation probability, which plays an effective role in the method's rate of convergence as well as the global optimisation seeking ability. The algorithm requires fewer iterations and is able to calculate the planning path faster.

Jian Zhang et al. introduced the gyratory solenoid to implement the genetic process and smooth planning paths separately [7]. Firstly, the paths are obtained by the genetic algorithm, and secondly, the gyratory solenoid function is used to replace the paths with large fold angles with rounded curves to achieve the effect of path smoothing. The algorithm not only improves the pathway's suppleness and the robot's movement process's safety, but also shortens the path length, simplifies the genetic algorithm itself, and increases the system's effectiveness operation.

7. RRT algorithm (Rapid Search Randomised Tree Algorithm)

The RRT algorithm is widely known for its simplicity and low complexity. Its basic idea is to imitate the traits of a branch in a tree branching from the beginning to the end of each random extension, then a related 2-way version from the beginning to the end of the extension of both ends, until the intersection of the two "trees" forks.The traditional version of the RRT algorithm usually traverses all the nodes in the map, which is prone to excessive computation in larger or more complex environments, or inaccessible to some narrow terrain.

Chen et al. expanded on the idea of bidirectional RRT by setting a third point at the midpoint of the straight-line distance between the start point and the end point, so that the four random trees are continuously extended in phase between the three points to obtain a path that is more convergent to the shortest distance [8]. At the same time, a special function is used to correct the random sampling point (i.e., the position of each random fork), so that each fork is purposefully oriented towards the end point, which significantly increases the algorithm's effectiveness.

And Zhou et al. proposed a unit partitioning method, which divides the map into small blocks of the same size and prioritises the search for the unit to which the node belongs, which avoids the defects of the algorithm that the traditional RRT needs to traverse the whole map [9]. This improves the directionality of the node search, and effectively reduces the computational volume of the algorithm.

Ying Yang et al. by introducing APF algorithm to provide gravitational force and repulsive force for the target and obstacle respectively, make the bifurcation of the random tree smoother in terms of obstacle avoidance while being more directional [10]. Secondly, the quality of path generation is improved by the sector region method to solve the problem that the RRT algorithm will resample several times during obstacle avoidance, and the paths are iteratively optimised by the Bessel curve formulation to obtain smoother paths at the end of path planning.

8. Artificial potential field algorithm(APF)

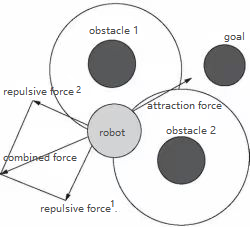
The artificial potential field method is a robot path planning algorithm that mimics the force field in modern physics. The algorithm takes the obstacle and the target node as the force field affecting the robot as the robot detects a repelling force from the impediment and the target point generates a gravitational force on it. The robot moves along the combined gravity force and repulsive force in the direction of the target node as a result of the joint action of the gravitational force and the repulsive force.(shown as Fig. 4).

Figure 4. Overview diagram of the principle of APF method.

The idea of this algorithm is very simple and the algorithm runs efficiently. It is easy to integrate and optimise with other algorithms, which is widely used. However, there are some glaring issues with the conventional APF as well. Such as the robot in some special cases into the force balance and can not move forward, due to mimic the role of physical repulsive force makes the robot can not stick to the obstacles to the goal node, so that the route sometimes can not reach the shortest, or in the obstacles around the goal or on the way to the goal node of the repulsive force causes the robot can not reach the goal node and so on. reach the goal node, etc.

For the more obvious problem that the robot stops due to force equilibrium, a common method is to add random gravitational points to break the force equilibrium around the robot, thus solving the problem of the robot getting stuck. However, this method is very unstable due to its random nature, and may lead the robot to deviate from its original route, resulting in a significant reduction in the accuracy of the generated shortest path, and sometimes even blocking the robot's original planned path, resulting in the algorithm failing to operate properly.Based on this problem, Xiang Yu et al. combined the A-star with the conventional APF, and through the improved A-star, the next node is generated and used as a virtual target node when the robot is caught in the force equilibrium, so as to break the equilibrium by using this node as a gravitational force point, and to make the robot move forward towards the newly added virtual target node [11].He et al. They avoided that the gravitational force of the target node would be too great to cause the robot to ignore the obstacles and directly crash into them by using the traditional artificial potential field method, in which the the force of gravity of the target node corresponds to its distance [12].

By contrast, Peng Qiu et al. improved the APF algorithm for path planning in terms of steering obstacle avoidance based on structured roads for robots with obstacle avoidance deficiencies during dynamic steering [13]. The method uses ellipticised distances instead of the actual distances simulated in the repulsive potential field and introduces a boundary repulsive potential field model, thus enabling the robot to obtain path planning for local obstacle avoidance in a relatively small space.

9. Artificial intelligence algorithm

The application of artificial intelligence algorithms in the field of path planning is gradually emerging, with features including learning capability, adaptability, global search capability, complex environment handling, non-deterministic handling, and real-time performance. They are capable of adjusting path planning in real time in dynamic environments, adapting to complex tasks, and dealing with uncertainty by learning environmental information and historical data.

10. Q-learning algorithm

The Q-Learning algorithm is a value-based reinforcement learning algorithm that mimics the learning behaviour of organisms; in short, organisms will be more inclined to perform behaviours that will be rewarded again, while avoiding behaviours that are easily punished. The algorithm does this by estimating the reward that the organism will receive for performing each behaviour, trial and error and obtaining an optimal solution by maximising the total future reward (i.e. the highest Q), and each time the organism is in a new state, it chooses to perform the behaviour that is known to have the highest Q in that state, and continually updates its Q table with the feedback given by the environment. The algorithm has a wide range of applications, and Q-Learning is currently the algorithm of choice for most tasks that require robots to perform in environments that are inaccessible to humans or where danger is unknown. However, the Q-Learning algorithm suffers from a blind exploration phase with frequent trial and error in the initial execution part, and this flaw is also a problem for most AI algorithms, which has a significant impact on the efficiency of the algorithm's operation.

The traditional Q-learning algorithm starts the operation with all the contents of the Q-value table as 0, and then the agent (which refers to the learning object) starts to learn and search blindly and randomly, which wastes a part of the algorithm's computational time and resources. Song Lijun et al. initialised the Q-value table by locating the Euclidean distance from the grid at any position to the target grid D(xi,xg), and the Euclidean distance from the grid at the start point D(xi,xx) by taking D(xi)=(l-n)-D(xi,xg)+n-D(xi,xx).

Use the linearly normalised value of D(xi) to initialise the Q value for each state [14], and in this way to skip the blind exploration stage, so that the algorithm has a tendency to choose the next target node in the early stage of the operation, which significantly boosts the algorithm's convergence efficiency while also discretizing the action space to speed up the AGENT's training and speed up resolution. Li et al. replace the rule of selecting the largest Q-value in the traditional Q-learning algorithm by a selection method related to the Q-value table, which reduces the influence of noise and the probability of falling into a local optimum during the algorithm's operation [15]. At the same time, the system training is accelerated by introducing prior knowledge from relevant task domains and setting up prior rules.

11. Deep learning algorithm

Deep learning is a series of intelligent algorithms inspired by the human brain's ability to process data and create patterns for decision making, and in recent years has seen major technological breakthroughs, and is now widely used in areas such as image processing, data analysis, and machine recognition. The broad applicability of the technique allows it to be combined with other algorithms in the field of path planning to gain a more comprehensive advantage.For example, Abdi et al. combined a deep learning algorithm with a Q-learning algorithm, where the former is responsible for learning and exploring the robot arm's modeling of its route, while the latter is responsible for exploring the angle control of the joints of the actuator at the terminal of the robotic arm [16]. A significant amount of computing work load and time is saved by utilizing the strengths of both algorithms to increase the algorithm's efficiency.

12. Hybrid algorithm

Many path planning algorithms have their own strengths and weaknesses in different aspects, and in the complex and changing real-world environments, it is difficult for a single algorithm to cover all the needs. Therefore, there are many attempts to combine two or even more algorithms so as to take advantage of their strengths, such as the hybrid algorithm combining deep learning and Q-learning algorithms mentioned in the previous section. [16] In some cases, hybrid algorithms can have multiple advantages that are difficult to combine with a single algorithm.

Yi Cao et al. combined the improved A-star algorithm and Dynamic Window Approach to fix the problems of discontinuous path curvature and low obstacle avoidance efficiency in mobile robot path planning [17]. Floyd's algorithm was introduced after simplifying the eight-way search of the traditional A* algorithm to a five-way search to improve the search efficiency, and a new heuristic search function was designed to achieve the smoothness of the route. To assure the overall path optimization of planning, impediments are avoided to the greatest extent by integrating the enhanced algorithm with DWA.

Yuan et al. hybridised the RRT algorithm with APF algorithm, using it to quickly obtain the optimal shortcut in the relatively open range of the environment, and using RRT for obstacle avoidance in the relatively small obstacle environment [18]. The hybrid algorithm not only makes up for the defect of the RRT algorithm that consumes excess arithmetic leading to the inefficiency of the algorithm in the complex situation of a large environment, but also avoids the deficiency of the traditional APF that cannot approach the target point when the obstacle is close to it by jumping out of the thinking range.

Hamdia et al. then substitute the principle of deep neural network learning into the genetic algorithm, through the genetic algorithm of the neural network output of some parameters such as the number of neural network layers [19]. The number of neurons in a single layer and so on for the exchange of combining as well as optimisation, which greatly improves the learning efficiency of the neural network.

13. Discussions

Intelligent search algorithms as well as artificial intelligence algorithms can present a blind search phase at the beginning of their operation due to their nature of optimising the outputs in the process to eventually arrive at an optimal solution. At the same time, there is also a possibility that they may get into some kind of deadlock at convergence and fail to produce the final result. These shortcomings limit the computational efficiency of traditional intelligent algorithms, so reducing or eliminating the effects of these shortcomings will be an important direction for future research in this area.

The applicability of path planning algorithms also needs to be related to the devices they are applied to in real-world environments, and the parameters in the algorithms need to be adjusted according to the specific needs of the devices, such as the need for smooth paths, the consideration of factors affecting the devices themselves in their physical environments, or collision avoidance and other needs that need to be taken into account when multiple devices are working together.

The special characteristics of hybrid algorithms make them have the advantages of multiple algorithms and can be widely applied to more complex environments. For this kind of algorithms, how to balance the advantages and disadvantages of multiple algorithms and maximise the efficiency after combining them will be an important research direction in the future, which also depends on the different needs of different devices.

14. Conclusions

The field of path-planning algorithms has made significant technological advances today, although sometimes the computational time or accuracy of some algorithms has to be sacrificed for the sake of comprehensive performance. As the experience accumulated in different fields continues to improve, and the related technologies in various fields continue to develop, path planning algorithms will eventually blossom in a more powerful arena in the future.

References