1. Introduction

As the core power unit of modern aircraft, aeroengines are of irreplaceable importance, and their performance is directly related to the overall flight performance and economy of the aircraft. In actual work, the flow field environment inside the engine is quite complex, and is affected by various gas dynamic phenomena such as boundary layer separation, shock wave interference, and vortex. Therefore, in the design process, high requirements are placed on the accurate prediction of the flow field. In flow field research, the current mainstream methods are mainly experimental research and numerical simulation. Although experimental methods such as wind tunnel experiments and vortex field experiments can provide relatively accurate flow field data, their implementation is usually accompanied by high economic costs and long cycle times. Experimental conditions often cannot fully reproduce the complex flow conditions that occur during actual flight, which to a certain extent limits the effectiveness of experimental methods. Numerical simulation, especially methods based on computational fluid dynamics (CFD), has been widely used due to its low cost and good flexibility. Numerical simulation can provide instant flow field prediction by mathematically modeling actual physical phenomena and combining the computing power of high-speed computers. However, this method also faces huge computational workload and high resource requirements. Especially under high Reynolds numbers and complex turbulent conditions, the prediction accuracy of numerical simulation still has large deviations.

Linse et al. [1] first applied neural network technology to the problem of aerodynamic parameter identification in 1993, pioneering the use of neural network models to model aerodynamic data. They established a normal force coefficient model for a twin-jet transport aircraft by simulating flight data, and verified the method with good results. The advantages and limitations of these methods are based on scientific inquiry, considering data as an inherent part of modeling, experimentation and simulation. Machine learning provides a powerful information processing framework. Machine learning algorithms can mine the mapping relationship between input data and output data from big data, which can enrich and even change the current development status of fluid mechanics research and industrial applications. White et al. [2] proposed a new method to solve the problem that computational fluid dynamics calculations on aerodynamic behavior take a lot of time. Some fluid mechanics modeling involves basic physical models, while others are model-free and only make predictions based on existing simulation data. A new neural network architecture, cluster network, was introduced. This structure has an inductive bias that is very suitable for fluid dynamics problems. Compared with model-based approximation methods, this method has accurate results, an error rate of less than 1%, and is one order of magnitude faster. At present, various convolutional neural network structures [3] have been applied to aerodynamic research and have been used to predict lift coefficients with given airfoil shapes and flow conditions. Zhao Y M of Peking University [4-5] proposed a data-driven turbulence modeling method, applied machine learning to the field of fluid mechanics, and used machine learning methods to develop turbulence models. Various types of turbulence modeling have been achieved. Dr. Zhao Y M mainly focuses on key fluid mechanics problems with the internal flow of aircraft engines as the background. He has achieved a series of new results in turbulence engineering modeling by using cutting-edge high-precision numerical simulation methods, machine learning and other methods. The generalized regression extreme value neural network method [6] can be used for blade life reliability analysis to achieve the purpose of improving the life and performance of turbine blades. Wang Chao et al. [7] proposed a large airspace and wide speed range aerodynamic modeling method, using artificial intelligence neural network technology to achieve high-precision approximation of full-trajectory aerodynamic data with multi-dimensional strong nonlinear characteristics. Chen H X et al. [8] summarized the history and current status of the application of machine learning in aerodynamic optimization, discussed the possible application forms of deep learning in aerodynamic optimization and partially verified them. The feasibility of artificial intelligence in aerodynamic optimization and modeling and possible application methods were analyzed. Ding D et al. [9] applied probabilistic neural networks to analyze the location and degree of icing on flight state variables, and conducted preliminary discussions on the situation where sensors cannot be installed on the aircraft or the sensor installation location is limited, providing effective analysis for aircraft icing detection. In the problem of predicting gas diffusion concentration [10], considering the relevant influencing parameters of time, space coordinates and concentration, constructing a model of input variables and output variables, artificial intelligence neural networks can produce accurate prediction results. Zhao Y et al. [11] applied convolutional neural networks to establish a mapping relationship between the bluff body shape and fluid force obtained by fluid mechanics calculation through sample training, and realized the prediction of the fluid force of a new bluff body. Zhang T J et al. [12] reviewed the current status and development history of artificial intelligence methods and their applications in aerodynamic modeling and advanced aircraft design. Artificial intelligence methods can mine startup data and assist in the aerodynamic optimization design of aircraft. They also proposed some scientific problems and future development challenges faced by the combination of artificial intelligence and aerodynamics. From the current research status at home and abroad, it can be seen that the combination of artificial intelligence in the field of aerodynamics is applicable, so it is feasible to apply machine learning and other methods in the analysis of the aerodynamic characteristics of the integral blade of an aircraft engine. The vibration failure of aircraft engines is mainly caused by complex flow fields, so how to establish a correct mathematical model of three-dimensional unsteady flow fields has become a key scientific issue. The development of artificial intelligence technologies such as neural networks and deep learning has provided new ideas for solving this scientific problem. Neural networks have the ability to find optimization solutions at high speed, can train sample data to find features, and realize corresponding predictions of data. The characteristics of the flow field are very suitable for applying neural network modeling.

This review studies the recent research on the application of machine learning in the field of aerospace, and aims to explore the possibilities of neural network models in flow prediction. Through this review, we hope that you can better understand the advantages of machine learning in flow field prediction and be able to apply them more widely in aerospace related problems. The structure of this review is as follows: Section 2 introduces the concepts and methods of machine learning. Section 3 The shortcomings of traditional flow field prediction methods at this stage. Section 4 focuses on three specific cases, including BP neural network, RBF neural network, and UNet neural network methods, and analyzes their current progress in flow field prediction. This article is summarized in Section 5.

2. Machine learning

Machine learning methods can be divided into supervised learning, unsupervised learning and semi-supervised learning according to whether the training data has labeled information. The data set of supervised learning contains existing labeled data. By building a model to learn a clear output relationship, new data can be predicted. Typical applications of supervised learning include classification and regression problems. Classification problems refer to dividing input data into pre-defined categories, such as image classification and email filtering; while regression problems refer to predicting a continuous value, such as stock price prediction and commodity price prediction. The task of unsupervised learning is to model and analyze data without labeled data to find structures and patterns in the data. Typical applications of unsupervised learning include clustering, anomaly detection and dimensionality reduction. Clustering refers to dividing data into several groups according to a certain similarity measurement method. The similarity of data within each group should be as high as possible, and the similarity between groups should be as low as possible. Anomaly detection refers to finding samples in the data set that are different from other data. Dimensionality reduction refers to mapping high-dimensional data into low-dimensional space, but trying to retain the key features and information in the data. Semi-supervised learning is between supervised learning and unsupervised learning. Its task is to build a model for unlabeled data by learning data with known labels when some data has labels and some data has no labels.

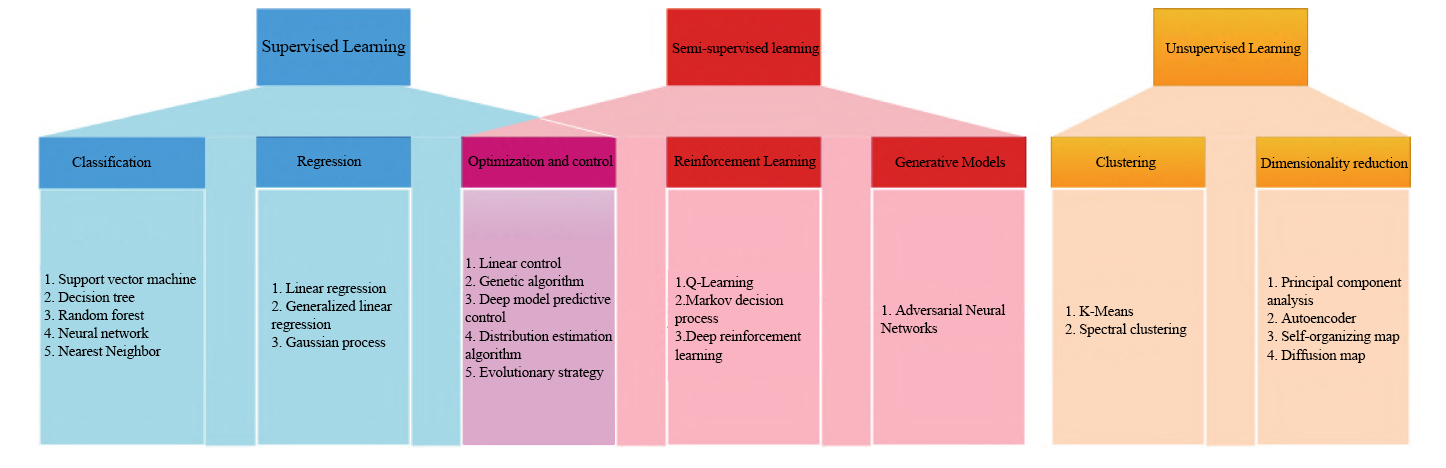
Figure 1. Classification of Common Machine Learning Methods

Figure 1 shows the main methods included in each of the three categories summarized by Brunton et al. [13]. Among them, the neural network model is one of the most powerful machine learning algorithms at present. It imitates the neuron structure of the human brain and realizes the processing and prediction of input data by constructing a multi-layer neural network. Here we briefly introduce some basic concepts in neural networks. Neurons are the basic units in neural networks. They receive an input and generate an output. The sum of the products of the input received by the neuron and its corresponding weight is used as the activation value of the neuron, and then a nonlinear transformation is performed through the activation function to achieve modeling of complex data. Multiple neurons are combined into layers according to certain rules, which can be used to extract different features of the input data. The neural network starts with the input and performs forward propagation, passing through multiple layers in sequence until the output result is output. The loss function can measure the difference between the model prediction result and the actual result, and serves as the objective function of model training. By calculating the error between the output result and the actual result, the error is back-propagated back to the neural network and the weight is updated to improve the prediction accuracy of the model. Common neural network models include multilayer perceptron (MLP), convolutional neural network (CNN) and recurrent neural network (RNN). Among them, MLP is the most basic neural network model, which consists of multiple fully connected layers and can be used for tasks such as classification and regression; CNN is suitable for processing image data and extracting spatial features of images through convolutional layers and pooling layers; RNN is suitable for processing sequence data, such as natural language or weather data.

3. Traditional flow field prediction methods

3.1. Wind tunnel test

In typical outflow wind tunnels for airfoils, missiles, and transport aircraft, each aviation power has established its own standard model system through standard model tests [14]. Plane blade test is an important basic test technology that is most widely used in the development of aircraft engines. It is a special type of wind tunnel built specifically to simulate the flow of blades of rotating impeller machinery such as fans/compressors/turbines [15]. It is a very important link in the design process of axial compressor blades. The United States [16-17], the United Kingdom [18-19], Germany [20], Russia and other countries have established authoritative plane blade wind tunnel test systems in the 20th century, and have accumulated rich and comprehensive test data for series of blades (NACA-65, BC-6, C-4, etc.) [21-22].

The wind tunnel test department of the Technical University of Darmstadt in Germany has launched a series of studies on the flow field of compressor blades. The research team used high-end measurement tools to successfully determine key parameters such as the pressure layout in the flow field and the structure of the vortex. These established experimental results provide in-depth and reliable information support for the discussion of digital modeling and academic theory. In my country, the wind tunnel laboratory of the University of Aeronautics and Astronautics of China has also made remarkable breakthroughs in scientific research. The experimental team conducted large-scale experiments and conducted in-depth research on the airflow pattern inside a certain type of compressor blade. Based on the collected experimental data, the research team designed a variety of optimization measures, which significantly improved the aerodynamic characteristics of the blades, with an increase of 10%. The blade flow field prediction technology of aircraft engine compressors at home and abroad has made significant progress. However, in the face of complex fluid characteristics, there are still many problems to be solved. For example, the current mathematical modeling and digital simulation technology are still not completely satisfactory in dealing with high turbulence, complex geometric shapes, etc. Although experimental research can provide us with extremely accurate data, its high cost and long-term needs do restrict its practice to a certain extent. Therefore, combining various technical methods to enhance the accuracy and effectiveness of flow field prediction continues to be a focal topic for future research.

3.2. Computational fluid dynamics

CFD technology is widely used in aerospace, marine engineering and other fields. The rapid improvement of computer performance and the development of various numerical calculation methods have made computational fluid dynamics technology gradually become the mainstream aerodynamic calculation method in the current fluid field. CFD technology directly starts from the basic equation of flow and can accurately reflect the nonlinear and unsteady characteristics of blade aerodynamic loads. It is one of the effective ways to study blade flow fields and provides a reliable basis for the research of aircraft engines. Some experts and scholars have conducted research on compressor blades based on computational fluid dynamics. Liou and Povinelli [23] outlined the research of the National Aeronautics and Space Administration (NASA) on computational fluid dynamics from 1947 to the present. The research content is divided into numerical calculation of fluid mechanics, physical modeling, development of CFD codes, verification of CFD codes and multidisciplinary design optimization. CFD technology is used to help analyze and design relevant parameters of aircraft engines, simulate engine components and configure complex three-dimensional flow fields.

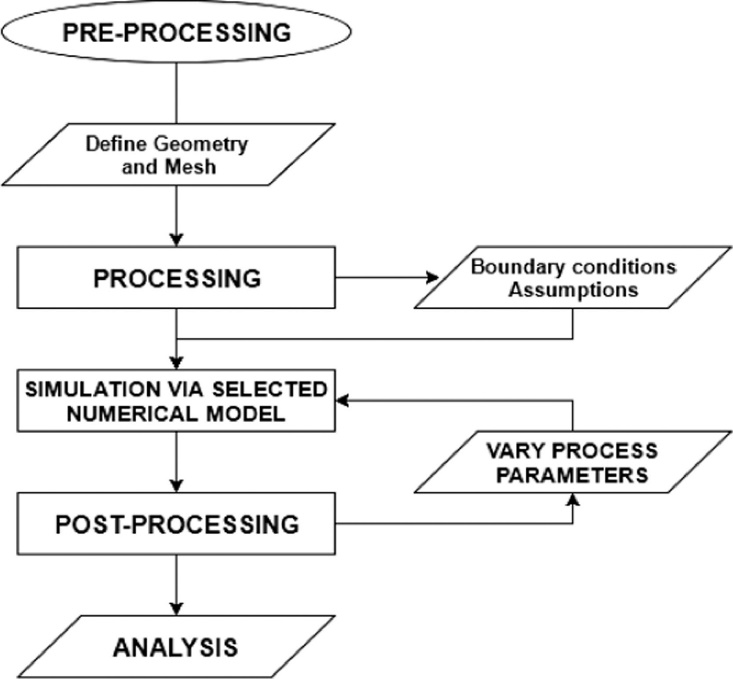
Figure 2. CFD calculation flow chart

Wang Hongyu et al. [24] used CFD theory and NUMECA software to numerically calculate the pressure distribution of the flow field in the sealing grate cavity of an aircraft engine, analyzed the influence of the rotation speed of the blade and the outlet static pressure on the aerodynamic force, and obtained the trend of the static pressure on the drum surface. The rotation speed and the outlet static pressure have different effects on the static pressure on the drum surface, and the influence of the outlet static pressure is more obvious. Santo et al. [25] used a high-fidelity fluid-solid coupling simulation method to analyze the influence of gusts on the blades of a large horizontal axis wind turbine. The model consists of a CFD model and a computational structural mechanics (CSM) model. The calculation results can better estimate the frequency of relevant data such as the blade load. The model can provide effective solutions to problems such as the installation of wind turbines. Zhu R et al. [26] established a 1.5MW horizontal axis wind turbine blade and flow field model based on ANSYS CFX fluid mechanics calculation software. By comparing the working state of the blades at different wind speeds, the differences in the unsteady flow field and structural vibration of the wind turbine blades under single and double-way fluid-solid coupling were studied. The aerodynamic characteristics and vibration changes of the blades were compared in detail, and the CFD analysis of the aerodynamic characteristics and vibration characteristics of the blades was realized. The flow field in the flow channel of the aircraft engine compressor contains strong nonlinear, three-dimensional, unsteady and complex turbulent flows in the transition process. Li et al. [27] used CFD to establish a flow channel model for the axial flow compressor blade, considering the viscous blade force model generated by the loss. The blade surface was modified and the prediction ability of the model under complex flow fields was verified. Duan et al. [28] improved the exact solution of the local Riemann problem on the blade surface and designed the compressor blade grid through CFD, which reduced the total pressure loss and smoothed the pressure load on the blade surface. Roberto et al. [29] developed and verified a CFD-based flow model and analyzed the blade section cascade of the turbine structure. Cozzi et al. [30] pointed out that when considering the important influence of radial mixing, the classical steady-state computational fluid dynamics method has a large deviation and cannot be applied to compressor aerodynamics. They improved the RANS model and applied it to the analysis of the compressor, improving the efficiency, pressure ratio and other characteristics of the compressor. Drewczynski et al. [31] used CFD to calculate the first-stage compressor blades of aircraft engines. Omidi et al. [32] designed different splitter blades and used the CFD method to correct the position of the leading edge and the crown of the blade.

Sangjo et al. [33] calculated the performance of an aircraft engine compressor at a certain operating point based on three-dimensional CFD. By improving the existing one-dimensional mean model, an equivalent model that can predict the compressor performance was generated. This method can be applied to a three-stage axial compressor of a certain type of aircraft engine. It predicts the performance of the compressor near the operating point better, and can also predict the performance of the compressor in surge and other conditions. Moreno et al. [34] used three-dimensional unsteady computational fluid dynamics to predict the surge load of a three-axis aircraft engine compressor system. Kyros et al. [35] used experimental measurement data and a two-dimensional CFD model to analyze the exhaust nozzle of an aircraft engine and conducted experimental and computational research on the pressure loss of the engine exhaust system. CFD was used to study and analyze the flow field of the engine exhaust part, establish a corresponding model, and propose an alternative technology to improve the thermodynamic cycle of an aircraft engine. The technology was experimentally verified and the results showed that it can minimize the pressure drop of the exhaust nozzle and effectively improve the performance of the aircraft engine.

4. Flow field prediction method using machine learning

4.1. Predict the flow field around the airfoil

In order to conduct machine learning, obtaining data is an important first step. Using the real geometric data of the compressor blades, ANSYS software can be used to simulate the aerodynamic loads of aircraft engine blades under different working conditions to obtain aerodynamic load data under different working conditions. CFX is a professional software for solving fluid dynamics analysis from ANSYS. It consists of three parts: pre-processing module (CFX-Pre), solver module (CFX-Solver) and post-processing module (CFX-Post). CFX adopts a finite volume method based on finite elements. On the basis of ensuring the conservation characteristics of the finite volume method, it absorbs the numerical accuracy of the finite element method [36-38]. First, the control equation is established. The three basic equations in fluid mechanics are the continuity equation, the momentum equation and the energy equation, which express the physical laws that fluid mechanics must follow. When fluid mechanics specifically expresses the law of conservation of mass, it is called the continuity equation, which is the law that must be followed in the process of analyzing any fluid flow. Any flow system must satisfy the law of conservation of momentum while satisfying the law of conservation of mass, which is called the momentum conservation equation. For some fluids with changing energy, the law of conservation of energy must also be satisfied, which is called the energy conservation equation. The rate of change of internal energy of a certain volume per unit time is equal to the sum of the heat generated in the volume of fluid and the heat given by the outside world. The compressor of an aircraft engine drives the shaft blade to rotate by converting the energy of the airflow into kinetic energy. The working environment of the blade is complex and unstable, and the workload is high.

Starting from the prediction of the flow field around a cylinder, the prediction results of machine learning methods in the prediction of Karman vortex street of low Reynolds number cylinder flow are studied. Ling Z G et al. [39] analyzed the computational efficiency and flow field calculation accuracy of different numerical simulation methods, and selected a numerical simulation result as a data set according to the actual situation to explore the application of machine learning methods in flow field prediction. Based on the prediction results, the flow field under the condition of Re=3500~5500 was learned, and the accuracy of neural network flow field prediction was analyzed. Finally, the algorithm was transplanted to the steady prediction of NACA0018 airfoil using the idea of transfer learning. The velocity scalar field, pressure scalar field and velocity vector field were predicted, and the accuracy of the algorithm was proved. The calculation time of the numerical simulation method and the machine learning method at the same accuracy level was compared. The calculation results were processed by using the calculation results to explore the calculation methods of airfoil vortex field, streamline and other parameters, and the pressure coefficient was integrated to solve the error between the airfoil lift and drag coefficient and the numerical simulation.

Neural networks based on machine learning methods require a large number of data sets and their corresponding relationships as sample space. Considering that the flow around the airfoil is relatively complex, and the airfoil can be transformed into a symmetrical airfoil through the Joukowski transformation, it can be seen from reference [40] that it is assumed that there is a circle with a radius of a on the ξ plane, and the circumference of the circle passes through the point ξ=c, with its center at the point (-m, 0), and m< <c. Therefore, its radius can be expressed as a=c+m=c(1+ε), assuming z = \( R∙e^{iθ} \) . As shown in the Joukowski transformation formula (4.1):

\( z=ζ+\frac{c^{2}}{ζ} \) (4.1)

Obtained formula (4.2)

\( z=c[1+ε(1-cos{θ})]e^{iθ}+\frac{c}{1+ε(1-cos{θ})}e^{-iθ} \)

A neural network model with a depth of eight layers is used. Excluding the input layer and the output layer, they are ReLU, SELU, ELU, SELU, Leaky ReLU, and Leaky ReLU. Using the idea of transfer learning, the method of attenuating the learning rate is used to enhance the prediction effect. The initial learning rate lr=0.005 is set, and the current learning rate is attenuated by 1% in each training cycle to achieve the purpose of global attenuation. The Adam optimizer is used to increase the number of training steps, and the number of training steps is set to 500. Due to the increase in the number of training steps, the L2 regularization method is used to prevent overfitting, and the regularization degree is set to 0.005, and the local weights are fine-tuned.

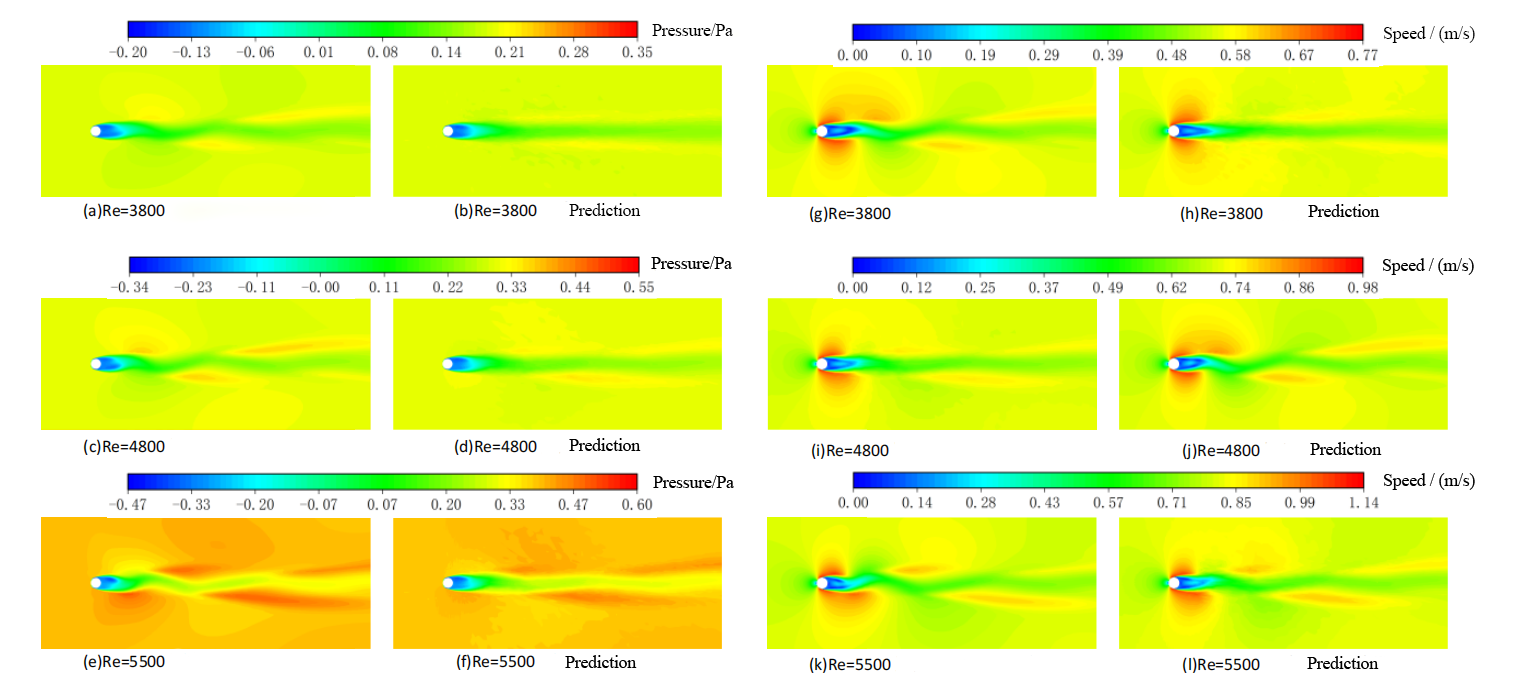
Figure 3. Comparison of pressure cloud map and velocity cloud map

As shown in Figure 3, when the Reynolds number is small, the pressure field error is more obvious, and the fluctuation prediction result of the vortex in the tail vortex area is poor. The reason is that when the Reynolds number is small, the pressure field values are very close, causing the neural network prediction to ignore the fluctuation of the tail vortex. With the increase of the Reynolds number, the prediction results gradually improve in the cloud map performance, but there are more confusions in the prediction results near the cylinder, the pressure field fluctuates greatly, and "pitting" and jagged transition areas appear in the cloud map. The reason is that the values change drastically there, and a large error occurs in the neural network fitting process. It also shows that the number of neural network training steps is too large, and overfitting occurs in local areas, and the prediction results show large foggy fluctuations. Considering the learning efficiency, a larger learning rate can be used in the early stage of training to accelerate the learning efficiency, and a smaller learning rate can be used in the later stage of training to obtain high accuracy. The method of deepening the neural network can also be used to optimize the prediction.

The airfoil flow field is calculated based on the neural network described in the case of flow around a cylinder. The structure uses the neural network for flow around a cylinder. However, due to the different number of data points, the neural network for airfoil prediction has two more hidden layers than the neural network for flow around a cylinder. The neural network structure shown in Figure 4 is used for prediction.

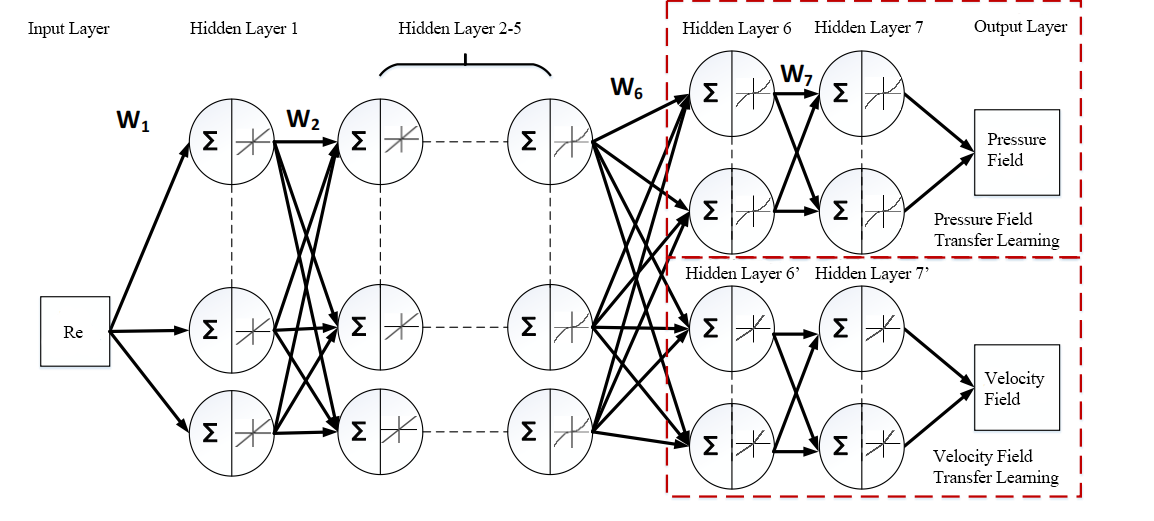
Figure 4. Neural Network Architecture

A custom activation function is added to hidden layer 7 to constrain the data, and the improved activation function is compared with the traditional activation function to verify the accuracy of the results. Regression model by merging high-fidelity CFD data, enabling the optimization of aerodynamic designs over a range of Mach values in an efficient and reliable manner.

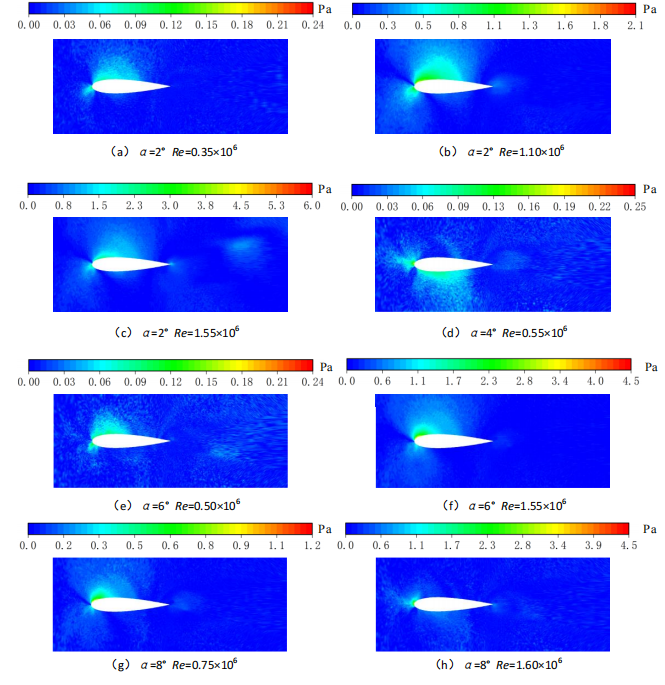
Figure 5. Comparison of pressure field error cloud maps

The error cloud map is made by combining the sample cloud map and the predicted cloud map. In 4.3, it can be seen that with the increase of the Reynolds number, the absolute error in the pressure field prediction error cloud map is mainly distributed near the front edge of the suction face and near the stagnation point. Analysis of the reasons shows that the pressure value changes greatly at this location, and the error is mainly concentrated in the low-pressure area of ​​the airfoil. With the increase of the Reynolds number, the neural network calculation error becomes larger and larger. And with the increase of the Reynolds number, the relative pressure on the upper wing surface decreases rapidly, resulting in an increase in the pressure gradient on the upper wing surface, causing the error to spread to the upper wing surface. When the Reynolds number increases to 1.6×106, the absolute error of the upper wing surface reaches the maximum and has filled the entire upper wing surface area. Without considering the change of the angle of attack, with the increase of the Reynolds number, the pressure prediction error near the stagnation point also gradually increases. Analysis of the data shows that the relative pressure near the stagnation point will mutate. From the analysis of the neural network structure and weight relationship, it can be seen that this situation is that the neural network has given up the high precision of some data in order to ensure the global optimality. In order to ensure the global optimal algorithm, the neural network requires the data to have consistent continuity, so it is difficult to make accurate predictions. In response to this problem, I personally believe that the neural network algorithm or data structure needs to be further improved in order to achieve the purpose of accurate prediction.

4.2. Prediction and analysis of blade linear pressure field

The basic idea of RBF neural network is: use RBF radial basis function as hidden unit, so that the input vector can be directly mapped to the hidden space. When the center of the radial basis function is determined, the mapping relationship is also determined. The mapping from the hidden layer to the output space is linear, that is, the output of the network is equal to the linear weighted sum of the outputs of the hidden layer units. Therefore, in general, the mapping from input to output of the designed network is nonlinear, but the output of the network is linear for adjustable parameters. The weight of the network can be directly solved by the linear equation, which greatly speeds up the learning speed and avoids the local minimum problem. The RBF neural network has a direct connection between the input layer and the hidden layer unit, has the characteristics of optimal approximation, and has no local minimum problem, avoiding the local optimum. The modeling data of the neural network comes from the simulation data of the flow field of the compressor blade of an aircraft engine under different conditions. There are 5 parameters in the input layer, namely the Reynolds number Re, Mach number Ma, density, rotational energy Ve, blade temperature T and other parameters of each sample point as the input data of the neural network, and the input vector is X=[Re,Ma, ,Ve,T]. The output layer is a single output, which is the static pressure of the sample point.Wang X Z et al[41]. used the model established based on the neural network for training prediction analysis, and verified the unstable data points of the blade surface obtained by computational fluid dynamics, and used RBF neural network to model the compressor flow field.

The aerodynamic data of the middle of the blade is selected as the training set, and the samples of the middle of the blade that are not used as the training set are selected as the test set to verify the accuracy of the model. Next, the trained neural network model is used to predict the root and tip of the blade respectively. Since the selected data dimensions are inconsistent, the data are scattered, and the sample span is large, the samples need to be preprocessed, that is, normalized, in order to reduce the data span, improve the generalization ability of the neural network, and facilitate modeling and prediction. Therefore, the corresponding data is normalized according to formula (4.3), where xi is the i-th component of the input vector, \( x_{i}^{max} \) , \( x_{i}^{min} \) are the maximum and minimum values of the i-th component respectively.

\( x_{i}=(x-x_{i}^{min})/(x_{i}^{max}-x_{i}^{min}) \) (4.3)

Figure 6 (a) shows the blade tip and blade root, as well as the middle area of the blade in the blade mesh division. The blade length is 160mm, the blade root is the 0-10mm area, and the blade tip is the 150-160mm area. Figure 6 (b) shows that the blade tip and blade root are at the upper and lower ends of the figure, respectively. The blade tip area is defined as Region 1 (R1), the blade middle area is defined as Region 2 (R2), and the blade root area is defined as Region 3 (R3). There are 8900 sample points and 100 linear data on the pressure surface of the compressor blade. Among them, there are 24 linear data in the blade tip area R1, 89 sample points in each linear shape, and a total of 2136 sample points. There are 52 linear data in the middle area R2 of the blade, 89 sample points in each linear shape, and a total of 4628 sample points. The blade root area R3 has 24 linear data, each with 89 sample points, for a total of 2136 sample points.

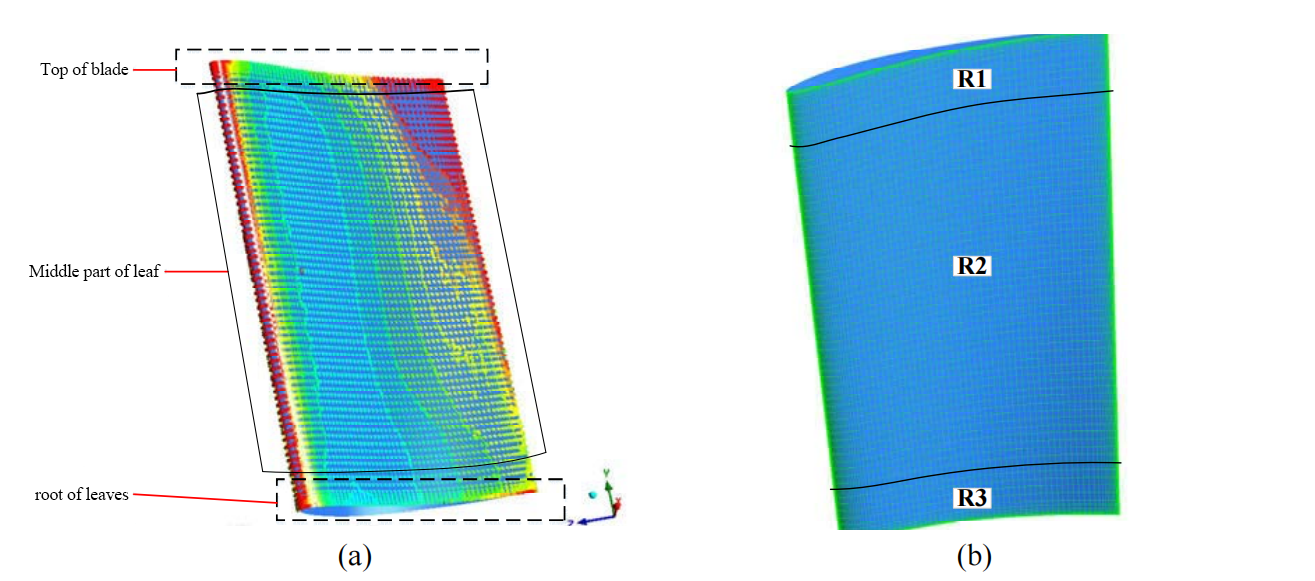
Figure 6. Selected blade linear data

First, the aerodynamic load data of the pressure surface of the compressor blade at a speed of 20000rpm is selected, and the aerodynamic data of the middle part of the compressor blade within the range of 10mm to 150mm is trained, with a total of 4628 sample points, of which 40 horizontal grid lines are divided into the training set, a total of 3560 sample points, accounting for 77% of the sample set, and the sample points are numbered from 2137 to 5696. Six horizontal grid lines are taken as the test set of the model, with a total of 534 sample points, accounting for 12% of the sample set, and the sample points are numbered from 5697 to 6230, to verify the reliability of the neural network model. Figure 7 shows the comparison between the trained data and the experimental values. The training set error is 0.24%. It can be seen that the fitting value of the RBF neural network at the simulation point is almost consistent with the experimental value, proving that the RBF neural network has a strong approximation ability for the nonlinear flow field data of the pressure surface of the compressor blade.

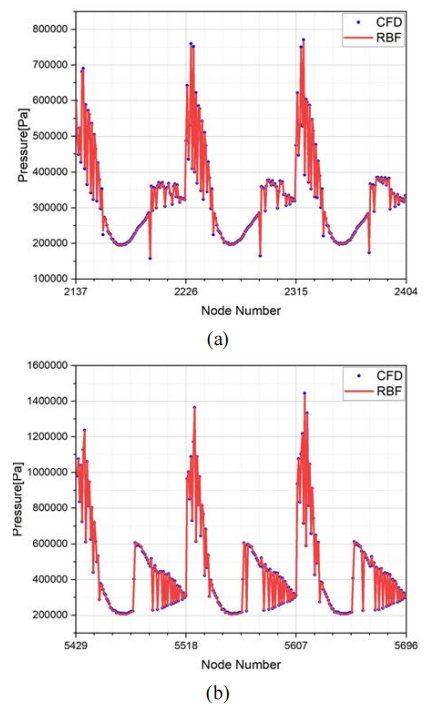
Figure 7. Blade pressure surface middle training diagram (20000rpm)

The sample points in the test set are numbered from 5697 to 6230. The 6 linear data in the middle of the blade are predicted. Figure 8 is a comparison chart between the predicted value and the CFD simulation, and the error is 0.48%.

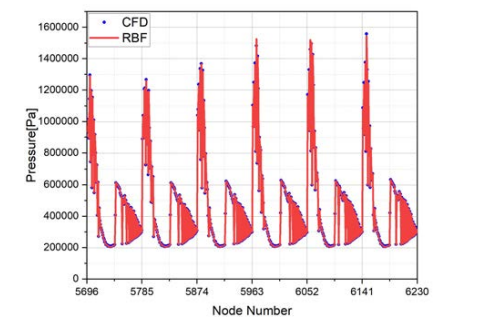
Figure 8. Blade pressure surface middle training diagram (20000rpm)

According to the RBF neural network model, the 24 grid lines in the linear data of the 0-10mm part of the blade root, a total of 2136 sample points, the 6 most edge lines, a total of 534 sample points, were selected for prediction; the 24 grid lines in the linear data of the 150-160mm part of the blade tip, a total of 2136 sample points, the 6 most edge lines, a total of 534 sample points, were selected for prediction. The error of the blade tip is 1.87%, and the error of the blade root is 1.05%. Figure 9 shows the prediction results of the blade tip 150mm-160mm. Figure 10 shows the prediction results of the blade root 0mm-10mm.

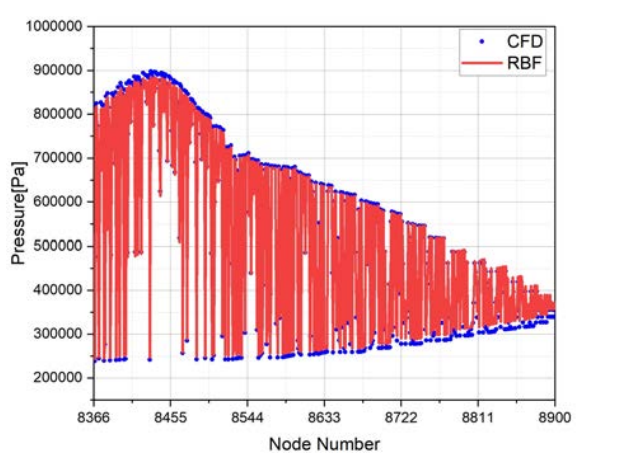
Figure 9. Blade tip prediction diagram (near 160mm section)

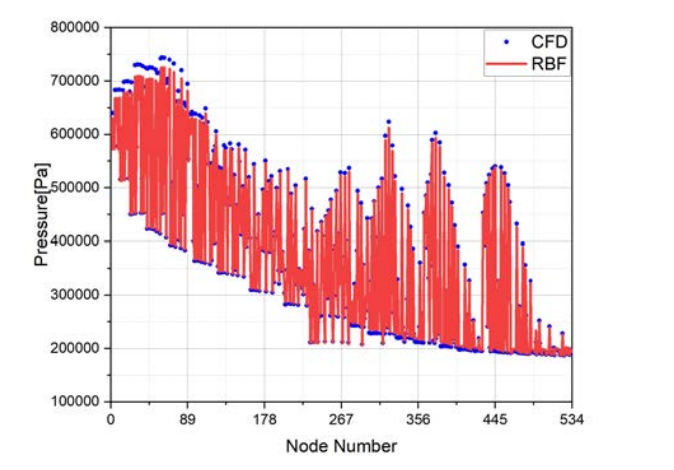
Figure 10. Blade tip prediction diagram (near 0mm part)

The internal flow field of an aircraft engine compressor is very complex, and traditional computational fluid dynamics requires a lot of time and cost in calculations and other issues. In order to quickly calculate the aerodynamic load data on the blade, the model of the surface pressure of the compressor blade pressure surface based on the RBF neural network predicts and analyzes the internal and external factors affecting the aerodynamic load of the blade, and the aerodynamic load data on the blade surface. The neural network model has a good prediction effect in the middle of the blade and at the extreme position of the non-blade edge, but the error is relatively large at the extreme position of the blade edge, especially the blade tip, which further illustrates that when CFD calculates the aerodynamic load data on the compressor blade surface, there will be unstable points at the extreme positions of the blade tip and blade root edge.

4.3. Machine learning inference method for airfoil flow field based on UNet

Machine learning methods represented by convolutional neural networks (CNN) have gradually become more important in industrial practices such as airfoil flow field simulation. Reference [42] used CNN to predict non-uniform laminar flow in two-dimensional automobile and three-dimensional hemispherical models in real time. Compared with traditional computational fluid dynamics simulation, this method can provide a solution speed that is 2 orders of magnitude faster than the GPU-accelerated lattice Boltzmann method (LBM) solver and 4 orders of magnitude faster than the CPU-based LBM solver. Compared with the LBM method, the average relative error of the CNN method in the two-dimensional automobile test set does not exceed 17%. Although the CNN method has a fast prediction speed, its accuracy cannot meet industrial needs. Reference [43] developed a multi-scale graph neural network model based on the encoder-process-decoder architecture for flow field prediction. Compared with the traditional CNN method, this model has better accuracy in the prediction tasks of airfoil flow field and flow around a cylinder. However, the prediction results of the model show discontinuous and unrealistic velocity and pressure distribution, and the predicted flow field lacks smooth physical characteristics. The main reason is that in order to maintain the connectivity of the graph at different scales, sparse matrix multiplication is required, which brings additional computational overhead and non-physical consistency. In the prediction of more complex airfoil compressible flow fields, more suitable models and algorithms are needed, and UNet is a more suitable choice because it can ensure that the flow field has scale invariance and high-resolution feature accuracy. Reference [44] explores the accuracy of the deep learning model inferring the Reynolds average Navier-Stokes (RANS) solution, focusing on the analysis of the effectiveness of the UNet network architecture in predicting the incompressible flow field of the airfoil. The flow field data used for model training are all from the numerical simulation of the RANS method in Open-FOAM. The study found that the size and weight of the training data have an impact on the accuracy of the model prediction. The model obtained under the optimal training strategy was used for prediction analysis in the test set, and the average relative pressure and velocity errors of the predicted flow field were less than 3%. The results show that in the prediction of airfoil flow field, by selecting a suitable model and adopting an excellent training strategy, a fast and high-precision machine learning flow field inference model can be obtained based on a data-driven method. Reference [45] proposed a method for using a supervised neural network to predict the velocity and pressure field of an obstacle of arbitrary shape in a two-dimensional laminar flow. It uses Bezier curves to construct a random obstacle shape data set, and uses the CFD method to simulate and calculate the shape flow field of each obstacle, and uses the pressure and velocity information in the flow field to train various UNet neural network architectures. Finally, it is proved that based on the rich geometric features of the data set, the trained neural network model has strong generalization and its prediction ability is physically explainable.

Although these results fully demonstrate the great advantages of using machine learning methods (neural network architectures represented by deep UNet) in airfoil flow field prediction, it is still very challenging to achieve engineering-level high accuracy and high robustness. Specifically, in most previous studies, the input of the neural network mostly uses the auxiliary Cartesian grid interpolation method to process the flow field data, and the geometric boundary information input to the neural network is represented by the signed distance function or binary mask, which results in the lack of generalization of the neural network model, poor prediction of separated flow, transition flow, shock wave/boundary layer flow, and poor robustness.

In order to further improve these disadvantages and realize the fast and high-precision prediction of the airfoil compressible flow field under different incoming flow conditions, Zhu Z J [46]proposes a CFD calculation coordinate and neural network coordinate transformation method for data preprocessing, develops a deep UNet neural network method for extracting advanced flow field features, and combines the two methods to carry out the study of efficient reasoning methods for airfoil compressible flow fields, and illustrates the fast and high-precision reasoning ability of the established model through multiple examples, and illustrates the excellent generalization ability of the model through generalization.

The airfoil flow field is complex and delicate, and the reasoning method proposed in this example has a lot of input information, so deep UNet is selected for model training. The encoder-decoder structure and jump connection module of the UNet network structure ensure that the features acquired by the model contain rich contextual information and retain some positioning details of the original input. As shown in Figure 11, the model proposed in this paper uses tensor information of size 12 as input and outputs tensor information of size 4, including pressure field, density field and velocity field in x and y directions. The model has 6 downsampling layers and 6 upsampling layers. Each downsampling layer consists of 1 convolution layer and 1 ordinary UNet block, and each upsampling layer consists of 1 ordinary UNet block and 1 transposed convolution layer. The deep UNet network architecture design enables the model to obtain better nonlinear expression ability, learn more complex transformations, and thus better fit complex input features.

Compared with the fully connected neural network (FCN), UNet has a completely symmetrical feature, and FCN only uses one deconvolution operation. When UNet is applied to the field of flow field prediction, as an overall end-to-end network architecture, training and using UNet does not require complex flow field pre-processing and post-processing steps; passing encoder features to the decoder through jump connections can effectively alleviate information loss in flow field learning and improve the prediction accuracy of complex flows such as boundary layers, shock waves, and flow separation; through its symmetrical network architecture, it can ensure that the flow field has scaling invariance and high-resolution feature accuracy. Therefore, UNet can rely on richer high-level abstract features to improve the generalization of the model while improving the accuracy of flow field prediction, and can also more accurately predict flow phenomena such as large separation flows and shock waves.

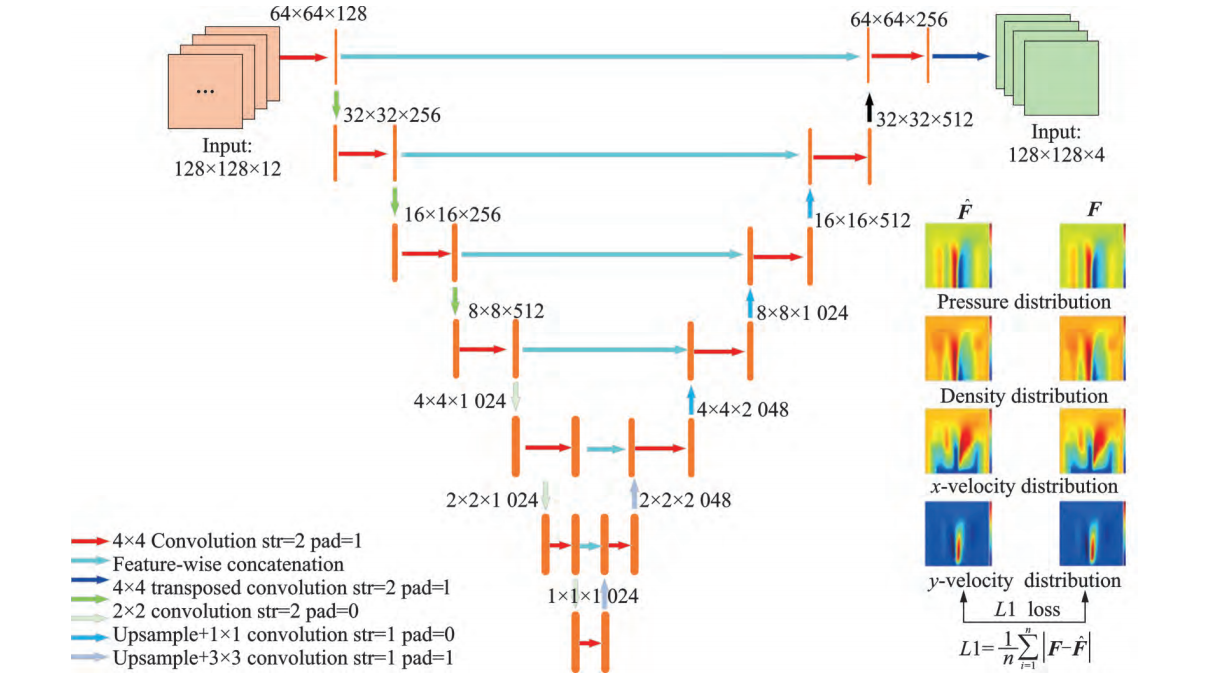
Figure 11. Architecture of UNet

The kc135d airfoil is selected for analysis. Under the free flow conditions of high Mach number and high angle of attack of Ma∞ = 0.70, AoA∞ = 5.68° and Re∞ = 4.537 × 106, as shown in Figure 12, the airfoil flow field reasoning method proposed in this paper can simulate the adverse pressure gradient caused by the weak shock wave on the upper wing surface under this state. As shown in Figure 13, the fast reasoning method proposed in this paper can accurately predict the local pressure change and local velocity change in the airfoil flow field, and can accurately predict the weak shock wave phenomenon on the upper wing surface. Combined with Figure 14, the error value MSE is reduced from 0.00641 of traditional machine learning to 0.00263. It can be seen that compared with the traditional machine learning method, the method in this paper has a strong advantage in reasoning weak shock waves, which are strongly associated with input conditions.

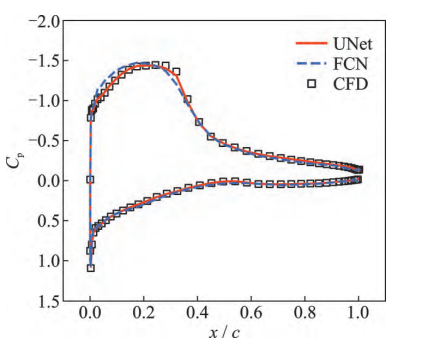
Figure 12. Pressure coefficient of kc135d airfoil

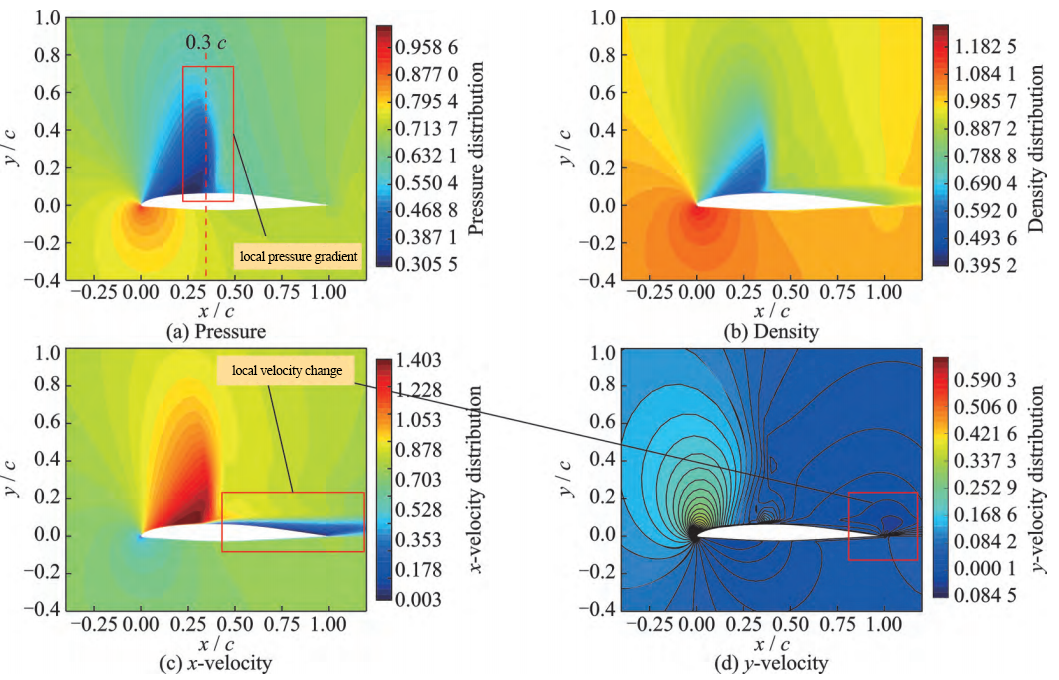
Figure 13. Flowfield prediction of kc135d airfoil

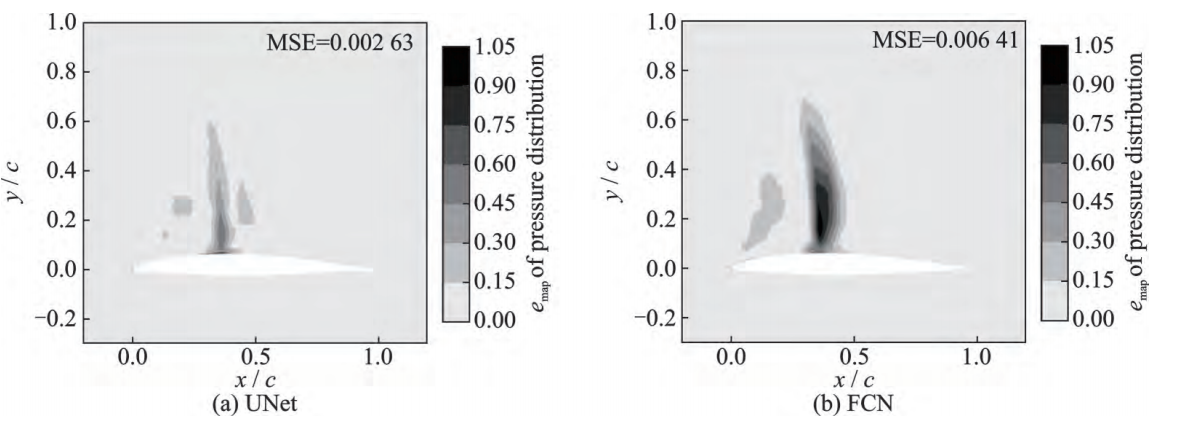
Figure 14. Prediction error of pressure distribution for kc135d airfoil

This coordinate transformation method for flow field data preprocessing converts CFD calculation space coordinates and flow field information into neural network space coordinates, making the input of flow field data more consistent with the UNet architecture specification, enabling the neural network to learn more flow details, boundary layer flow and global reasoning of the flow field. The deep UNet architecture for flow field data learning, through the corresponding downsampling architecture, cascade architecture, encoding module and deep network of UNet, after inputting the coordinate-transformed flow field data, UNet can better extract its area of interest, learn the high-level features in the airfoil, incoming flow conditions and flow field mapping, and thus construct a neural network model with high sensitivity to the incoming flow Reynolds number, Mach number, airfoil shape and angle of attack. Compared with the traditional FCN, the flow field prediction task is carried out in different characteristic airfoils and different incoming flow conditions. In places where the flow field gradient changes greatly, the pressure coefficient of the airfoil surface inferred by this method is better consistent with the CFD method, and the shock wave and flow separation phenomenon under the high Mach number incoming flow condition with large angle of attack can be more accurately predicted.

5. Conclusions and further discussion

By applying machine learning models, some progress has been made in the prediction of complex flow fields in aircraft engine compressors, providing a new feasible method for the field of aerospace engineering. Our goal is to promote this new method to the aviation industry and discuss its potential applications in various aerospace engineering problems. This review first briefly introduces the concept of machine learning, then introduces some problems and defects in traditional flow field prediction methods, and finally reflects the success and shortcomings of machine learning in flow field prediction through three specific cases. The results of these studies highlight the potential for further development of prediction models based on neural networks and emphasize the importance of continuing research in this field. In the future, with the continuous advancement of computer computing power and the continuous accumulation of data, the use of machine learning will become more and more extensive, and high-precision, fast response and low-cost computing requirements can be achieved. This will greatly shorten the design cycle and design cost of aircraft engines.