1 Introduction

With the high frequency of the occurrence of disaster, it becomes more and more crucial to investigate the measures to handling the emergency incidents, which may have a hazardous influence to the safety of the public health, property damage, environment disruption and so on. According to statistics [1], in each year, the emergency incidents would lead to the loss of 3,096,400 million in mainland, China. Also, the data shows the increasing frequency of these kinds of emergency incidents, like toxic spill accidents, the earthquake and the inundation and etc. It is worth noting that the emergency incidents itself is not the main factors to cause the fatality and economic losses. The lack of efficient evacuation measures and the chaotic rescue efforts may be the most important reason. Owing to the delay or the congestion of the evacuation organization, a large fraction of people is trapped in the disaster area which lead to a serious result to the safety of people and property. It is obvious that the efficient organization of evacuation play an important role in handing with these kind of emergency incidents. However, according to the categories of disasters, the specific requirements and corresponding measures are quite different from each other. Short distance evacuation is common in fire and explosion, which is related to the walking distance with people. This kind of evacuation is highly related to the pedestrian flow theory. In the previous research, the pedestrian flow problem is similar to the fluid mechanics, and researchers use the model in fluid mechanics. However, the pedestrian on the road or the hallway is usually undirected which is different from the fluid. Thus, Helbing proposed a social force model to model the reaction between different people and the interaction between people and environment. This model has been widely used in many fields like pedestrian evacuation and pedestrian simulation model. Another kind of evacuation is carried out with a long-distance. This kind of problem often involves with a massive leak and spread of radioactive material or severe natural disasters. In the context, the evacuation needs to be finished with the assistance of transportation vehicles, like cars, helicopter, drone and trucks. In this direction, the road network, the features of the vehicles and the traffic flow becomes more crucial, which could have significant influence on the efficiency of evacuation. Additionally, the choices of each vehicle directly determine the flow distribution of the existing traffic network, if each vehicle make their decision based on their own interest to minimize their own cost or travel time. In such an emergency situation, it is easy to lead to a chaotic traffic organization and reduce the evacuation efficiency. Actually, many research have been conducted to investigate the nature of short distance as well as long distance evacuation. For example, the networking modeling as well as operational techniques are applied in the field to find the minimum evacuation route considering various constraints like road capacity, roader’s preference and vehicle speed. The inter programming, dynamic programming, minimum cost flow problem and mixed programming are applied to solve this problem as a single objective or multi-objective optimization problem. In conclusion, the evacuation problem is one of the most important and complicated problem that needs to be solved, since it is related the public safety and involves a lot of aspects of society like efficient organization, resource distribution and humanitarianism. The higher and more efficient the evacuation will be, the more people or property would be saved.

2 Related work

As mentioned above, evacuation problem has been investigated for a long time. To the best of my knowledge, there are two groups of research which focused on the short-distance and long-distance evacuation problem respectively.

The first direction mainly focused on the short-distance evacuation. Previous research of this direction investigates the relationship between different categories of people, the effect of group effect and the interaction between the choice of environment like the wall, barrier and the construction structure. Fruin was the first to proposed that the physiological and psychological factor could have an significant influence on the choice of pedestrians. The next, Henderson measured the speed distribution function which is consistent with the Maxwell-Boltzmann theory. Based on the previous research, the most influential mode social force model is proposed by Helbing and Molnar. This theory is considered as the fundamental theory of microscopic pedestrian theory and have been applied in the pedestrian simulation software and evacuation analysis, especially simulating the evacuation process when emergency incidents occur. With the development of computer science and new technologies, the cellular automation has attracted more and more attentions from 1990s, which is firstly proposed by Neumann. It is considered that the social force model as well as the cellular automation lay the foundation of the pedestrian flow analysis using mathematical calculation. Another method to analysis the people’s behavior of evacuation is to conduct experiment and obtain the available data which could help researcher to understand the behavior in evacuation. And animal experiment is considered as a good way to address the lack of data on human evacuation. However, there is also some limitation about this method, since the difference between human and animals is hard to measure and there may be some experiment error which may lead to irrational results. Recently, with the wide use of smart phone using GPS, it becomes more accessible to obtain the data in evacuation. For example, Tian [2] proposed a novel method to analyze big data clusters from smart cities efficiently.

The research which focused on the long-distance evacuation usually simplifies the real word as a network. The term "network" is commonly used to describe a structure that can be either physical (e.g., streets and intersections or telephone lines and exchanges, etc.) or conceptual (e.g., information lines and people, affiliation relationships and television stations, etc.). Each of these networks includes two types of elements: a set of points and a set of line segments connecting these points. This observation leads to the mathematical definition of a network as a set of nodes (or vertices or points) and a set of links (or arcs or edges) connecting these nodes). In a network, it is possible to start from a original node to the destination node following the available path or link. Usually, a path is a sequential directed links. With this network setting, Yamada solve the rescue problem after the earthquake, they describe the problem as a minimum cost flow and shortest path problem and find that it is different when the road has capacity limitation or not. Campos applied the heuristic algorithms to find the optima routs between the origin and destination node. Dunn investigate the evacuation problem in the are of nuclear power station. They regarded this problem as a maximum flow problem and aims to transport more people within a limited time considering the constraints of road capacity. It is worthy to mention that all the research mentioned above is modeled in a static framework. When considering the departure time, this problem becomes more complex and can be modeled in a dynamic optimization problem. Hamacher did a review and summarization of the dynamic evacuation research about the maximum flow problem, dynamic fastest flow and dynamic maximum flow problem. They do some analysis about the potentiality about applying these methods to the evacuation problem. Lu [3] investigates the route selection, start time and destination optimization problem, and find that some improvements need to down about the algorithms in different kinds of problem.

This report is going to do some practical examples about the basic evacuation planning problem and try to code it in the MATLAB to find the final solutions. A simple network is applied in this report, but I believe that the technique is applicable to a more complex network to minimize the cost and find the maximum flow. In the next section, I try to do some basic introduction about the maximum flow problem and minimum cost flow problem as well as the algorithms to solve it.[4]

3 Evacuation optimization model

3.1 Maximum flow problem

In this model, it is expected that the flow from the origin to the destination through a specific path is the maximum within a short time. In a typica directed graph \( G = (V , E) \) , each links \( (i, j)∈E \) has a road capacity c. If \( (i, j)∉E \) which means that the link doesn’t exist in the network, assume \( c_{ij} = \) 0. And in this network, there are two special nodes called origin node and destination node, which means that all the flow departure from origin node and finally reach the same destination node. There are three constraints about the problem, the first is about the capacity constraints. It is obvious that in each link, the corresponding flow should be equal or less than the road capacity. The second constraints are about each node, in each node the inflow volume should equal the outflow volume. The third constraint is about flow equivalent constraints, which identify the flow departure from the origin node should equal the flow reach to the destination node [5]. Based on the above-mentioned definition and notations, the maximum flow problem can be described as following:

\( Max f \) (1)

St:

\( \sum_{j:(i,j)∈E}x_{ij}-\sum_{j:(i,j)∈E}x_{ji}= \begin{cases}f, i=s \\ -f, i=t \\ 0, i≠s,t\end{cases} \) (2)

\( 0≤x_{ij}≤c_{ij}, ∀(i,j)∈A \) (3)

About this specific optimization problem, we could apply the Edmond-Karp (EK) method to solve it. This method is firstly proposed by Dinic [6]. The basic idea of this method is to identify the augmenting path. Augmenting path means that the flow of corresponding path is less than the path capacity, in this situation, there is some quota left to increase the flow. And all the residual capacity could make up the residual network [7]. The formulation of residual can be depicted as \( r_{ij} = c_{ij} - f_{ij} \) . The procedure of this algorithms is to consider the feasible flow which satisfy all the constraints at the beginning, the simplest solution is the zero-flow pattern. Suppose we start with the zero-flow pattern, then it is easy to obtain the difference between the road capacity and traffic flow \( r_{ij} = c_{ij} - f_{ij} \) . The next, we find the minimum \( r_{ij} \) in a corresponding path, and if we add this volume into the network, it is obvious the solution will satisfy the constraints as well. And we find the augmenting path. We could repeat this process until that no augmenting path could be find, and the maximum path could be identified.

The next, we apply this method to solve a specific network problem. Assume given the network as shown in figure 1.

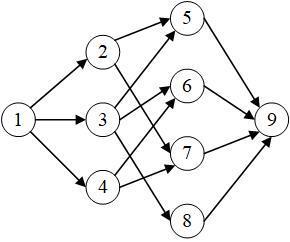
Figure 1. Network

The capacities are presented in table 1 and the code in MATLAB is presented in appendix A. It is mentioned that all the numerical experiments are designed and conducted with a MATLAB R2018a code performed on an Intel(R) core (TM)-I7 CPU 3.2 GHz with 8GB RAM.

Table 1. Road capacity.

The solutions are obtained as following:

Table 2. Solution to maximum flow problem.

3.2 Minimum cost problem

In the evacuation planning problem, it is common to regard the total cost as the objective to optimize. In this model, not only the flow in each path will be considered, but also the cost should be included. The unit cost of each link \( u_{ij} \) are defined as each unit flow go through this link would generate a cost of \( u_{ij} \) . This kind of network are defined as the capacity-cost network. It is also needed to satisfy a lot of constraints like capacity constraints, flow equivalent constraints and the inter-node flow constraints which is the same to the maximum flow problem mentioned above. The only difference is about the objective function. In this problem, the aim of the model is to minimize the cost. The problem is described as following:

\( Max \sum_{(i,j)∈A}u_{ij}x_{ij} \) (4)

St:

\( \sum_{j:(i,j)∈E}x_{ij}-\sum_{j:(i,j)∈E}x_{ji}= \begin{cases}f, i=s \\ -f, i=t \\ 0, i≠s,t\end{cases} \) (5)

\( 0≤x_{ij}≤c_{ij}, ∀(i,j)∈A \) (6)

Where \( x_{ij} \) represents the flow in each link, \( u_{ij} \) denotes cost when unit flow goes through the link, \( f_{i} \) is the flow that need to be evacuated in each node and \( c_{ij} \) is the road capacity.

It is worth noting that the algorithm to solve this problem is to using iteration method. This method is firstly proposed by Busacker and Gowan. The major idea in to find a feasible minimum cost path regarding the cost as the distance. And then assign the traffic volume as much as possible to this path. And then update the flow and cost of the reverse edge \( (j, i) \) . Do the iteration in the new updated network until we can not find the minimum cost path.

In the next, we do a simple calculation about this optimization problem based on the network depicted in figure 1. The corresponding cost are presented in table 3. The code is presented in appendix B.

Table 3. Cost.

After input the cost matrix, capacity matrix into the MATLAB, we can obtain the results as following:

Table 4. Solution to minimum cost problem.

4 Conclusion

The integration of machine learning into structural health monitoring represents a significant advancement in the field, offering versatile and efficient methods for detecting both local and global damage across various infrastructure types. The use of artificial neural networks (ANNs) and deep neural networks (DNNs) has proven effective in recognizing surface defects, such as cracks and spalling, within localized areas of concrete structures, including bridges, highways, and tunnels. This development has made it possible to address specific damage at a granular level, leading to more targeted and efficient maintenance efforts. Furthermore, low-cost solutions, like smartphone-based assessments, have demonstrated practicality and affordability in evaluating road integrity, expanding accessibility to critical monitoring technology.

Global damage detection, on the other hand, has focused on large-scale structural failures, employing advanced techniques such as feature extraction and deep learning to classify collapse modes and damage types more accurately. These methods help to enhance the resilience of infrastructure by enabling more effective early-warning systems and prompt interventions, potentially minimizing the impact of disasters.

In addition to the technological advances in damage detection, the broader implications of these innovations in emergency management should not be overlooked. With increasing occurrences of disasters such as earthquakes, toxic spills, and severe weather events, efficient evacuation and emergency response measures become crucial. Combining advanced machine learning models with existing evacuation and traffic management strategies can significantly improve the organization and coordination of emergency responses, ultimately reducing fatalities and economic losses.

Therefore, the continued development and integration of machine learning and computer vision in structural health monitoring will be critical for enhancing infrastructure resilience and public safety. Future research should focus on refining these models to accommodate diverse structural contexts and developing real-time monitoring systems that can inform emergency decision-making processes. Such advancements promise to transform the landscape of structural health monitoring, making it more robust, proactive, and accessible.