1 Introduction

In the field of modern industrial automation control, precise and efficient control systems play a crucial role in enhancing product quality, optimizing production processes, and ensuring the stable operation of systems. The PID (Proportional - Integral - Derivative) controller, as a classic and widely applied control strategy, has been used in numerous industrial processes for a long time due to its simple structure, ease of implementation, and good control performance. However, with the increasing complexity of industrial production and the ever - rising requirements for control accuracy, the traditional integer - order PID controller has gradually revealed some limitations.

The traditional PID controller is based on the integer - order calculus theory. Its three basic control parameters (the proportional coefficient, the integral coefficient, and the derivative coefficient) often struggle to achieve the desired control effect when dealing with systems featuring complex dynamic characteristics, non - linearity, time - variability, and large time - delays. For example, in the chemical production process, the complexity of chemical reactions leads to strong time - variability and non - linearity of process parameters. The traditional PID controller finds it difficult to maintain excellent control performance throughout the entire production process.

The emergence of the fractional - order PID controller provides new ideas for solving these problems. The fractional - order PID controller introduces fractional - order calculus based on the traditional PID controller, adding two adjustable parameters: the integral order and the derivative order, along with the original proportional coefficient, integral coefficient, and derivative coefficient, totaling five parameters. The proportional coefficient can respond rapidly to system deviations and adjust the control quantity in a timely manner; the integral coefficient is used to eliminate the steady - state error of the system; the derivative coefficient predicts the changing trend of the system and takes control actions in advance. The newly introduced integral order can flexibly adjust the intensity and time characteristics of the integral action, and the derivative order can describe the dynamic changes of the system more accurately, enhancing the control ability for complex systems. This endows the controller with greater flexibility and adaptability, enabling it to describe and control systems with complex dynamic characteristics more precisely. The fractional - order calculus theory can better depict the memory and hereditary characteristics of systems, which is of great significance for many practical engineering systems, such as heat conduction systems and material damping systems.

However, the performance of the fractional - order PID controller depends to a large extent on the rational tuning of its parameters. How to effectively tune these five parameters (, , , , and ) of the fractional - order PID controller to make it achieve the best control effect in different systems has become a research hotspot and difficulty in the current control field. Existing parameter tuning methods, such as methods based on empirical formulas, trial - and - error methods, and some intelligent optimization algorithms, have achieved certain results to some extent, but still suffer from problems such as complex tuning processes, large computational amounts, and slow convergence speeds.

Therefore, this paper aims to examine the most commonly used intelligent algorithms at present, such as the improved sparrow search algorithm, genetic algorithm, and GWO algorithm. These algorithms can improve the efficiency of fractional-order PID parameter tuning, increase the stability of the system, or automatically adjust the parameters of the system, thereby reducing the situation of manual intervention.

This study compares the effects of three intelligent algorithms in parameter tuning. It reveals the prospects of genetic algorithm in the field of fractional-order PID control in the future.

2 FOPID parameters tuning based on ISSA

Due to the initial solution dependence of the sparrow search algorithm and its tendency to fall into local optimal solutions and other issues, Chen Xuanru, Wu Lifei and Yang Xiaozhong proposed an improved sparrow search algorithm [2].

ISSA uses Chebyshev chaotic mapping to initialize the population, applies adaptive t-distribution and the firefly algorithm to obtain the transition probability p and conducts dynamic selection, thereby improving the optimization search effect of ISSA.

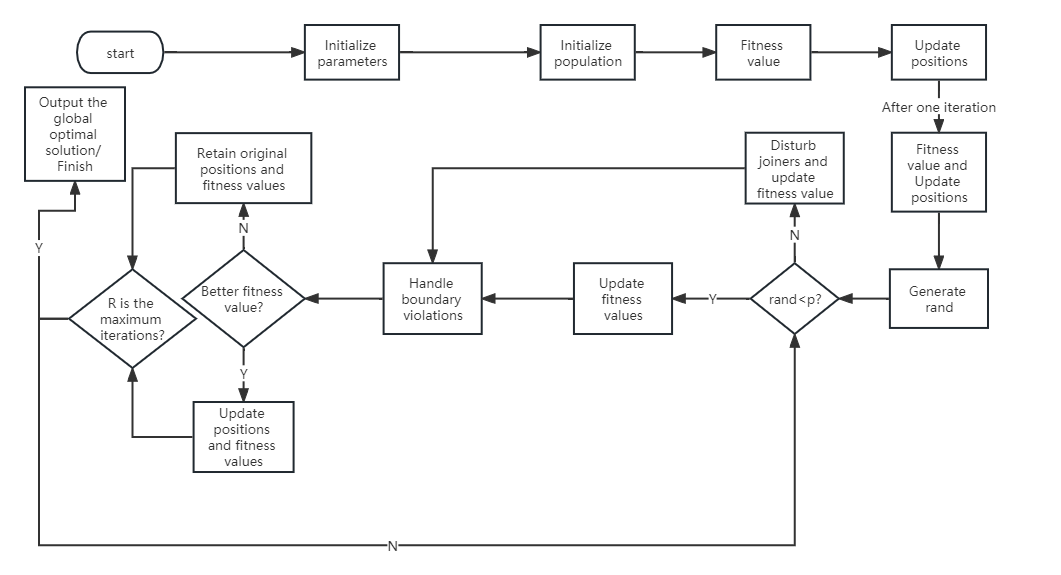
Figure 1. Flowchart of ISSA

The flowchart of ISSA is shown in Figure 1. In the flowchart, initializing parameters is the initialization of parameters such as population size and problem-solving dimension, and Chebyshev initialization mapping is used [2]. Updating fitness values and positions after one iteration is the change of sparrow fitness values and positions after updating predators, joiners, and sentinels [2]. The generated random number rand is compared with the transition probability generated by the adaptive t-distribution and the firefly algorithm. If the random number is less than the transition probability, a disturbance is generated; otherwise, the fitness is updated by using the firefly algorithm. The following are the specific steps for parameter tuning by ISSA: First, initialize population size N, problem-solving dimension d, discoverer ratio PD, sentinel ratio SD, sentinel warning value ST, transition probability p, upper bound u_b and lower bound l_b of initial value, and maximum number of iterations T_max. Second, initialize the mapping of the population. Third, calculate the fitness values of sparrows and sort them. Fourth, sparrows update the positions of predators, joiners, and sentinels. Fifth, after one iteration, calculate the fitness value and update the sparrow position. Sixth if \( rand \lt p \) , update the sparrow fitness value ; if \( rand ≥ p \) , perturb the joiners and update the fitness value of the sentinels. Seventh, handle boundary violations. If the new fitness value becomes better, update the position and fitness value; otherwise, retain the original ones. Eighth, determine whether the current iteration number R has reached T_max. If so, end the loop and output the global optimal solution; otherwise, return to sixth step.

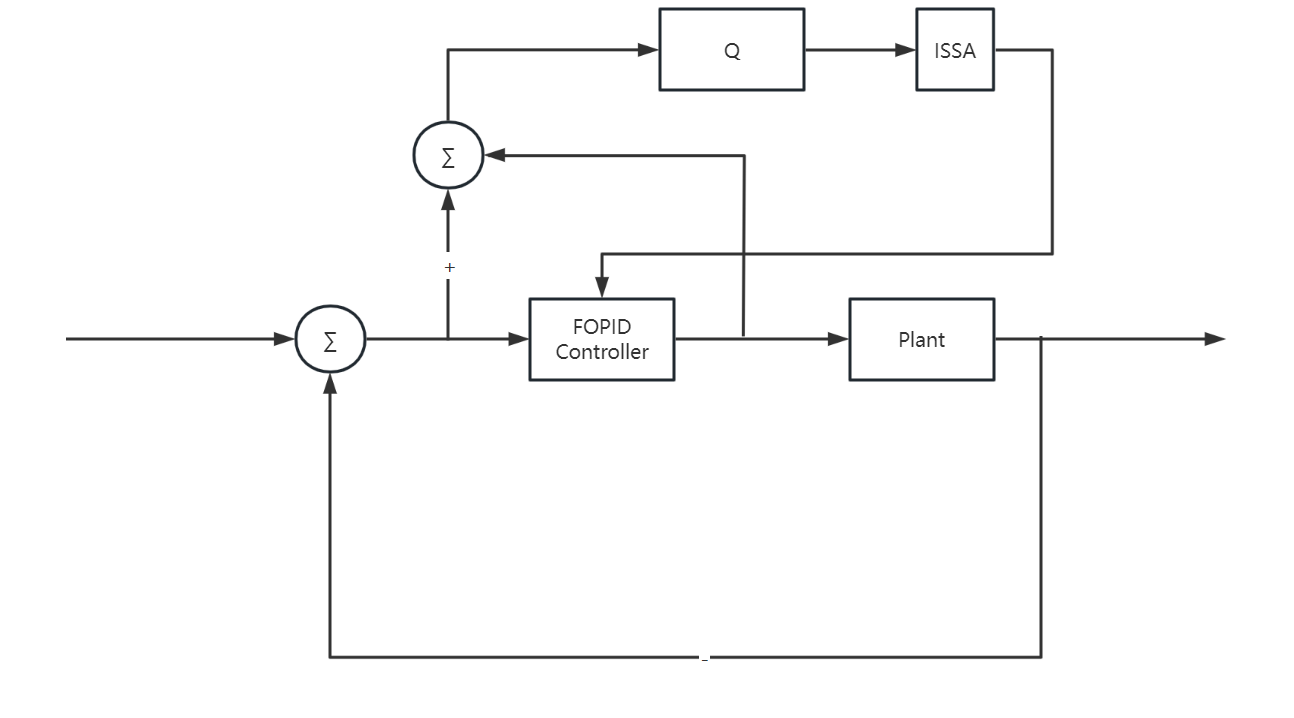
Figure 2. Design Block Diagram of FOPID Controller Based on ISSA Algorithm

The fractional PID controller model is designed based on the improved sparrow search algorithm as shown in Figure Figure 2, and the transfer function of the fractional PID controller is

\( G(s)= \)

Use ISSA to find the optimal set of parameters to meet the requirements of the system. To obtain satisfactory dynamic features of the iterative process, the evaluation function Q is as follows:

\( e(t) \) is the error between the output value and the input value; \( u(t) \) is the control value; \( w_{1} \) and \( w_{2} \) are between [0,1]; in order to prevent overshooting, an overshoot term is introduced in the original formula \( w_{3}|e(t)| \) .

The optimal aspect of ISSA lies in its high solution ability when solving multi-modal problems [2]. In addition, ISSA has excellent solution accuracy, solution speed and robustness.

3 FOPID parameters tuning based on GWO

Grey Wolf Optimizer (GWO) is a group intelligent optimization algorithm proposed by the scholar Mirjalili et al. in 2014. The algorithm is inspired by the hunting behavior of gray Wolf groups in nature, and simulates the leadership level and hunting mechanism of gray wolves [3]. Individuals in the pack were divided into four levels based on their physical strength and leadership. As shown in Figure 3, The rank from top to bottom is α, β, δ and ω

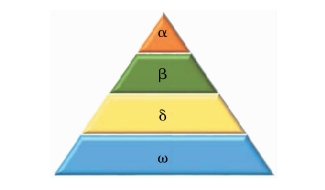
Figure 3. Population rank of the GWO[4]

In the GWO algorithm, the main steps are encircling, hunting, and attacking. First, the gray Wolf needs to judge the distance of the prey during the hunting process, and the following formula is used to calculate the distance of the prey in the GWO algorithm:

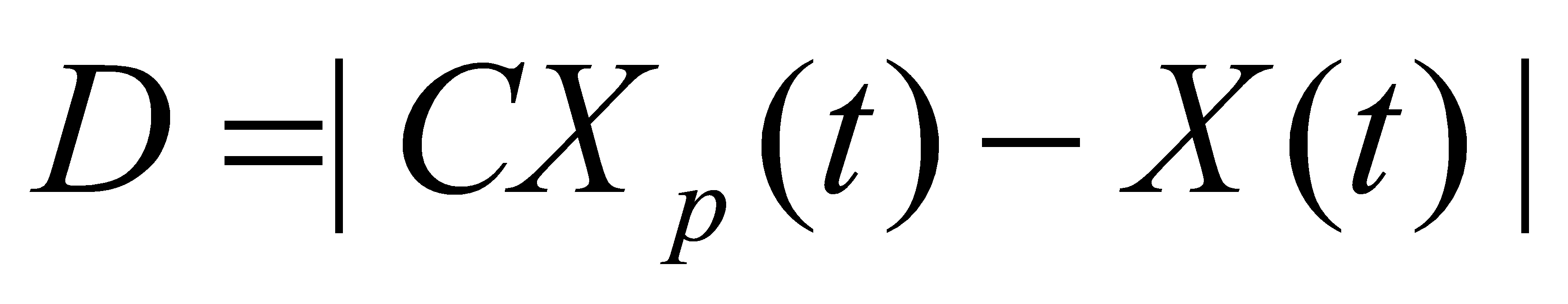
Where D is the distance, C is the coefficient vector, and t is the number of iterations, \( X_{p}(t) \) is the position vector of the prey, and \( X(t) \) is the position vector of the Wolf

After the grey Wolf determines the distance, it will update its position according to the following formula:

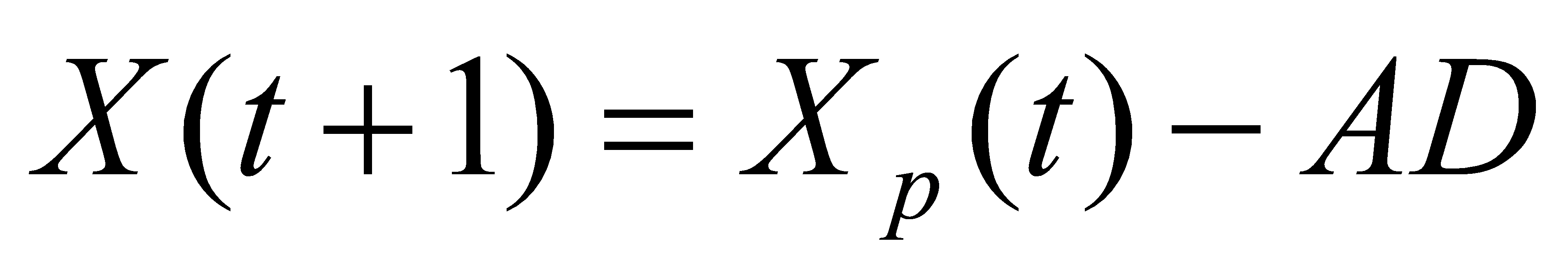
Where A is the coefficient vector and \( X(t+1) \) is the updated location of the grey Wolf. The grey Wolf algorithm uses the value of A to determine whether to conduct a local search or a global search. When \( |A| \lt 1 \) , the Wolf would choose to attack the target, and when \( |A| \gt 1 \) the Wolf would continue to update the location. After many iterations, GWO can find the optimal solution of the problem. However, because the linear search ability of the grey Wolf algorithm is prone to find the local optimal solution, Min Chao etc. uses the nonlinear search method to improve GWO by adjusting the search method in the GWO [4]. The initialization of the more realistic grey Wolf population can further optimize the traditional GWO, as studied by Yuyan Jiang etc. , combining the Holton sequence with GWO increases the global search ability of the algorithm [5]. In addition, the genetic algorithm can be used for the optimization of GWO [6], and the next chapter will discuss the setting of the fractional PID parameters of the genetic algorithm.

4 FOPID parameter setting based on the genetic algorithm

The genetic algorithm is founded on the principle of survival of the fittest. It is a self - organizing and adaptive artificial intelligence technique that emulates the natural biological evolution process and mechanisms [7]. The fundamental elements of the genetic algorithm (GA) encompass encoding and decoding, the fitness function, selection strategy, crossover operation, and mutation operation. Among these, the fitness function serves as the yardstick for evaluating the quality of individuals. Typically, it is a transformation of the objective function, mirroring the concept of adaptability in biological genetics. The selection operation involves choosing superior individuals from a population according to a pre - determined probability of change, analogous to natural selection in nature. As an illustration, consider the vehicle ABS fractional PID control with genetic algorithm - tuned parameters. For the precise control of the vehicle's ABS system, Chen et al. compared the braking distance [8], braking time, and over - regulation of the slip rate response among different methods. They then proposed a fractional PID controller based on the genetic algorithm. The fitness function of this scheme is as follows:

\( J=\int_{0}^{∞}w_{1}|e(t)|+w_{2}μ^{2}(t)+w_{4}|e(t)| \)

Where, \( w_{1} \) , \( w_{2} \) , \( w_{3} \) and \( w_{4} \) are the weight values of each part, taking 0.999, 0.001, 100 and 10 respectively, \( e(t) \) is the systematic error, \( μ_{t} \) is the control input, ts is the adjustment time, and \( t_{s} \) is 0.1s here.

Under the same genetic condition, the parameters to obtain the optimal fractional PID are as follows:

\( K_{p}=36.51 K_{i}=4.84 K_{d}=2.92 λ=0.14 μ=0.87 \)

After simulation analysis and the results into simulation results table:

Table 1. simulation result

As can be seen from the table 1, the fractional PID controller has smaller optimization parameters, giving the car a shorter braking distance, shorter braking time and smaller overshoot. Therefore, the fractional order PID has a better control effect.

5 Conclusion

This paper focuses on the parameter tuning of fractional-order PID (FOPID) controllers. By exploring different intelligent algorithms, namely ISSA, GWO, and GA, valuable insights into optimizing FOPID parameters have been obtained. The improved sparrow search algorithm overcomes the limitations of the basic sparrow search algorithm through techniques like Chebyshev chaotic mapping initialization, adaptive t-distribution, and the firefly algorithm. This enables it to effectively tune FOPID parameters, demonstrating high solution accuracy, speed, and robustness in handling multi-modal problems. The grey wolf optimizer, inspired by the hunting behavior of grey wolves, has its own set of procedures for encircling, hunting, and attacking. Although it has the potential to find optimal solutions, its linear search tendency may lead to local optima. However, researchers have proposed various improvement methods such as nonlinear search strategies, realistic population initialization, and combination with other algorithms to enhance its performance. The genetic algorithm, based on the principle of survival of the fittest, utilizes encoding and decoding, fitness functions, selection, crossover, and mutation operations. Taking vehicle ABS control as an example, the genetic algorithm-based FOPID controller shows better performance than the traditional PID controller in terms of braking distance, braking time, and overshoot.

In conclusion, different intelligent algorithms offer distinct advantages in FOPID parameter tuning. The choice of algorithm depends on the specific characteristics of the system and the control requirements. Future research can focus on further improving these algorithms or exploring hybrid methods to achieve even better control performance. This study provides a comprehensive reference for the application and development of FOPID controllers in industrial fields.